Dada una función f(x) continua en [a,b], vamos a buscar un polinomio P_n(x) de grado n

${\displaystyle P_n(x)=a_1{x}^n+a_2{x}^{n-1}+\mathrm{...}+a_{n}x+a_{n+1}}$

tal que la integral

${\displaystyle E={\displaystyle \underset{a}{\overset{b}{\int }}{\left(P_n(x)-f(x)\right)}^{2}dx}}$

sea mínima. Para calcular el mínimo, se deriva respecto a a₁, a₂...a_n+1

${\displaystyle \frac{\partial E}{\partial a_i}=0i=\mathrm{1,2,...}n+1}$

Obtenemos el siguiente sistema de n ecuaciones con n incógnitas

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{\partial E}{\partial a_1}=0\Rightarrow {\displaystyle \underset{a}{\overset{b}{\int }}{x}^n\left(a_1{x}^n+a_2{x}^{n-1}+\mathrm{...}+a_{n}x+a_{n+1}-f(x)\right)}dx=0\\ \mathrm{...}\\ \frac{1}{2}\frac{\partial E}{\partial a_n}=0\Rightarrow {\displaystyle \underset{a}{\overset{b}{\int }}x\left(a_1{x}^n+a_2{x}^{n-1}+\mathrm{...}+a_{n}x+a_{n+1}-f(x)\right)}dx=0\\ \frac{1}{2}\frac{\partial E}{\partial a_{n+1}}=0\Rightarrow {\displaystyle \underset{a}{\overset{b}{\int }}\left(a_1{x}^n+a_2{x}^{n-1}+\mathrm{...}+a_{n}x+a_{n+1}-f(x)\right)}dx=0\end{array}}$

o bien,

${\displaystyle \begin{array}{l}{a}_1{\displaystyle \underset{a}{\overset{b}{\int }}{x}^{2n}dx}+a_2{\displaystyle \underset{a}{\overset{b}{\int }}{x}^{2n-1}dx}+\mathrm{...}+a_n{\displaystyle \underset{a}{\overset{b}{\int }}{x}^{n+1}dx}+a_{n+1}{\displaystyle \underset{a}{\overset{b}{\int }}{x}^{n}dx}={\displaystyle \underset{a}{\overset{b}{\int }}{x}^{n}f(x)dx}\\ \mathrm{...}\\ a_1{\displaystyle \underset{a}{\overset{b}{\int }}{x}^{n+1}dx}+a_2{\displaystyle \underset{a}{\overset{b}{\int }}{x}^{n}dx}+\mathrm{...}+a_n{\displaystyle \underset{a}{\overset{b}{\int }}{x}^{2}dx}+a_{n+1}{\displaystyle \underset{a}{\overset{b}{\int }}xdx}={\displaystyle \underset{a}{\overset{b}{\int }}xf(x)dx}\\ a_1{\displaystyle \underset{a}{\overset{b}{\int }}{x}^{n}dx}+a_2{\displaystyle \underset{a}{\overset{b}{\int }}{x}^{n-1}dx}+\mathrm{...}+a_n{\displaystyle \underset{a}{\overset{b}{\int }}xdx}+a_{n+1}{\displaystyle \underset{a}{\overset{b}{\int }}dx}={\displaystyle \underset{a}{\overset{b}{\int }}f(x)dx}\end{array}}$

Llamando

${\displaystyle \begin{array}{l}{s}_k={\displaystyle \underset{a}{\overset{b}{\int }}{x}^{2n+1-k}dxk=\mathrm{1,2,...2}n+1}\\ b_k={\displaystyle \underset{a}{\overset{b}{\int }}{x}^{n+1-k}f(x)dxk=\mathrm{1,2,...}n+1}\end{array}}$

Escribimos el sistema de n ecuaciones con n incógnitas de forma matricial

${\displaystyle \left(\begin{array}{ccccc}{s}_1& s_2& \mathrm{...}& s_n& s_{n+1}\\ s_2& s_3& \mathrm{....}& s_{n+1}& s_{n+2}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ s_n& s_{n+1}& \mathrm{...}& s_{2n-1}& s_{2n}\\ s_{n+1}& s_{n+2}& \mathrm{...}& s_{2n}& s_{2n+1}\end{array}\right)\left(\begin{array}{c}{a}_1\\ a_2\\ \mathrm{...}\\ a_n\\ a_{n+1}\end{array}\right)=\left(\begin{array}{c}{b}_1\\ b_2\\ \mathrm{...}\\ b_n\\ b_{n+1}\end{array}\right)}$

Despejamos el vector a de las incógnitas utilizando el operador división por la izquierda \

Aproximación de la función e^x a un polinomio de segundo grado

Calculamos los coeficientes a₁, a₂ y a₃ del polinomio P₂(x)=a₁x²+a₂x+a₃

El sistema de ecuaciones en forma matricial se escribe

${\displaystyle \left(\begin{array}{ccc}{s}_1& s_2& s_3\\ s_2& s_3& s_4\\ s_3& s_4& s_5\end{array}\right)\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right)=\left(\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right)}$

Los elementos de la matriz s_k vales

${\displaystyle s_k={\displaystyle \underset{-1}{\overset{1}{\int }}{x}^{2n+1-k}dx=}{\frac{x^{2n+2-k}}{2n+2-k}|}_{-1}^1=\{\begin{array}{l}0k\text{par}\\ \frac{2}{2n+2-k}k\text{impar}\end{array}}$

Para obtener los elementos del vector b, integramos por partes, o bien, con la ayuda de Math Symbolic

>> int('x^2*exp(x)',x,-1,1)
ans =exp(1) - 5*exp(-1)
>> int('x*exp(x)',x,-1,1)
ans =2*exp(-1)
>> int('exp(x)',x,-1,1)
ans =exp(1) - exp(-1)

${\displaystyle \begin{array}{l}{b}_1={\displaystyle \underset{-1}{\overset{1}{\int }}{x}^2{e}^{x}dx}={x^2{e}^x-2x{e}^x+2e^x|}_{-1}^1=e-\frac{5}{e}\\ b_2={\displaystyle \underset{-1}{\overset{1}{\int }}x{e}^{x}dx}={x{e}^x-e^x|}_{-1}^1=\frac{2}{e}\\ b_3={\displaystyle \underset{-1}{\overset{1}{\int }}{e}^{x}dx}={e^x|}_{-1}^1=e-\frac{1}{e}\end{array}}$

El sistema de ecuaciones es el siguinte

${\displaystyle \left(\begin{array}{ccc}\frac{2}{5}& 0& \frac{2}{3}\\ 0& \frac{2}{3}& 0\\ \frac{2}{3}& 0& 2\end{array}\right)\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right)=\left(\begin{array}{c}e-\frac{5}{e}\\ \frac{2}{e}\\ e-\frac{1}{e}\end{array}\right)}$

El siguiente script representa en el intervalo [-1,1], la función e^x y el polinomio P₂(x)=a₁x²+a₂x+a₃

A=[2/5,0,2/3;0,2/3,0;2/3,0,2];
e=exp(1);
b=[e-5/e;2/e;e-1/e];
a=A\b;
p=@(x) polyval(a,x);
hold on
fplot(@exp,[-1,1]);
fplot(p,[-1,1])
hold off
legend('exponencial','polinomio','location','northwest')
grid on
xlabel('x')
ylabel('y')
title('Aproximando exp(x) a un polinomio')

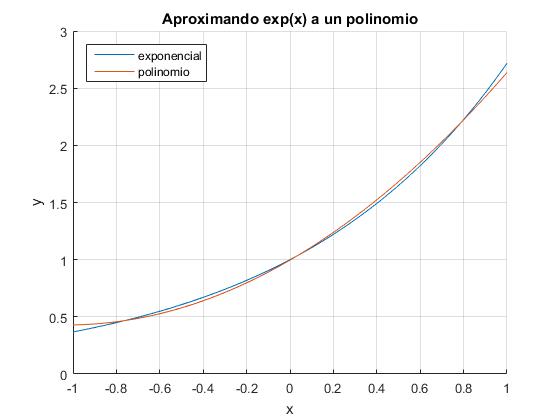
Como vemos en la figura hay una diferencia apreciable entre la función y el polinomio de segundo grado P₂(x)=a₁x²+a₂x+a₃, cuyos coeficientes son

a =
    0.5367
    1.1036
    0.9963

Aproximación de la función e^x a un polinomio de tercer grado

Elaboramos un script que nos permita aproximar la función e^x a un polinomio de grado n, P_n(x) en el intervalo [-1,1]. Sea por ejemplo, n=3

n=3; %grado del polinomio
syms x;
s=zeros(2*n+1,1);
for k=1:2*n+1
    if rem(2*n+2-k,2)==0
        s(k)=0;
    else
        s(k)=2/(2*n+2-k);
    end
end
A=zeros(n+1,n+1);
for k=1:n+1
  A(k,:)=s(k:n+k);
end
b=zeros(n+1,1);
for k=1:n+1
    f=exp(x)*x^(n+1-k);
    b(k)=int(f,x,-1,1);
end
a=A\b;
p=@(x) polyval(a,x);
hold on
fplot(@exp,[-1,1]);
fplot(p,[-1,1])
hold off
legend('exponencial','polinomio','location','northwest')
grid on
xlabel('x')
ylabel('y')
title('Aproximando exp(x) a un polinomio')

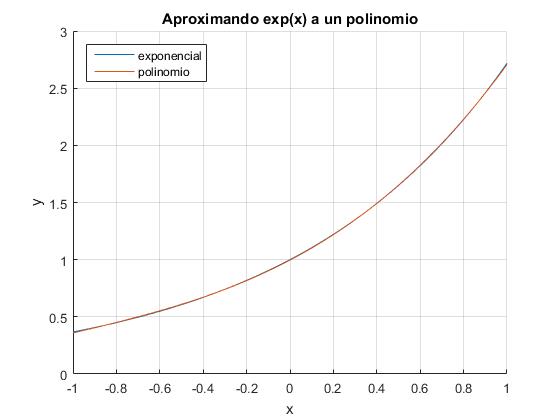
Como vemos en la figura ya no hay apenas diferencia entre la función y el polinomio de tercer grado P₃(x)=a₁x³+a₂x²+a₃x+a₄, cuyos coeficientes son

a = 
    0.1761
    0.5367
    0.9980
    0.9963

Aproximación de la función sin(πx) a un polinomio de segundo grado

Aproximamos la función sin(πx) a un polinomio de segundo grado en el intervalo [0,1]

Los valores de s_k y de b_k se calculan del siguiente modo

${\displaystyle \begin{array}{l}{s}_k={\displaystyle \underset{0}{\overset{1}{\int }}{x}^{2n+1-k}dx=}{\frac{x^{2n+2-k}}{2n+2-k}|}_0^1=\frac{1}{2n+2-k}\\ b_k={\displaystyle \underset{0}{\overset{1}{\int }}{x}^{n+1-k}\sin \left(\pi x\right)dxk=\mathrm{1,2,...}n+1}\end{array}}$

n=2; %grado del polinomio
syms x;
s=zeros(2*n+1,1);
for k=1:2*n+1
    s(k)=1/(2*n+2-k);
end
A=zeros(n+1,n+1);
for k=1:n+1
  A(k,:)=s(k:n+k);
end
b=zeros(n+1,1);
for k=1:n+1
    f=sin(pi*x)*x^(n+1-k);
    b(k)=int(f,x,0,1);
end
a=A\b;
p=@(x) polyval(a,x);
f=@(x) sin(pi*x);
hold on
fplot(f,[0,1]);
fplot(p,[0,1])
hold off
legend('sin(\pix)','polinomio','location','northwest')
grid on
xlabel('x')
ylabel('y')
title('Aproximando sin(\pix) a un polinomio')

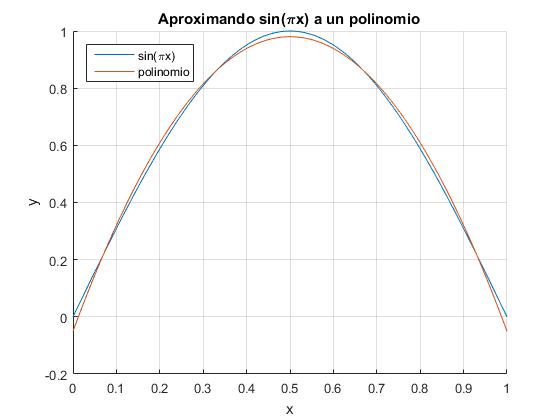
Como vemos en la figura ya hay poca diferencia entre la función sin(πx) y el polinomio de segundo grado P₂(x)=a₁x²+a₂x+a₃, cuyos coeficientes son

a =
   -4.1225
    4.1225
   -0.0505