Se define la función integral exponencial

${\displaystyle \text{Ei}\left(x\right)={\displaystyle \underset{-\infty }{\overset{x}{\int }}\frac{e^t}{t}dt}}$

fplot(@(x) ei(x),[0,4])
grid on
xlabel('x')
ylabel('Ei(x)')
title ('Función Ei(x)')

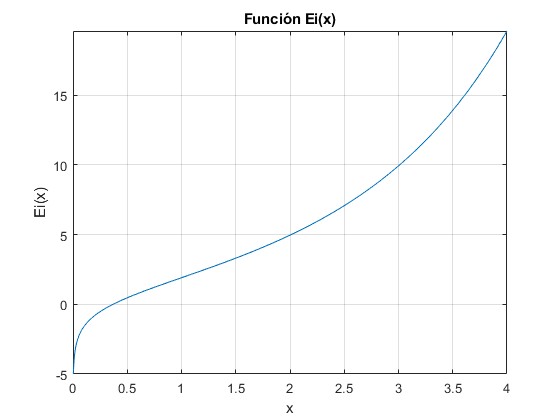
Utilizaremos esta función para calcular la integral

${\displaystyle {\displaystyle \underset{a}{\overset{b}{\int }}\frac{e^t}{t}dt}=\text{Ei}\left(b\right)-\text{Ei}\left(a\right)}$

Por ejemplo, sea a=2 y b=7. Calculamos la integral por dos procedimientos

• Utilizando el procedimiento numérico integral
• Utilizando la función ei

>> integral(@(t) exp(t)./t, 2, 7)
ans =  186.5505
>> ei(7)-ei(2)
ans =  186.5505

Producen el mismo resultado

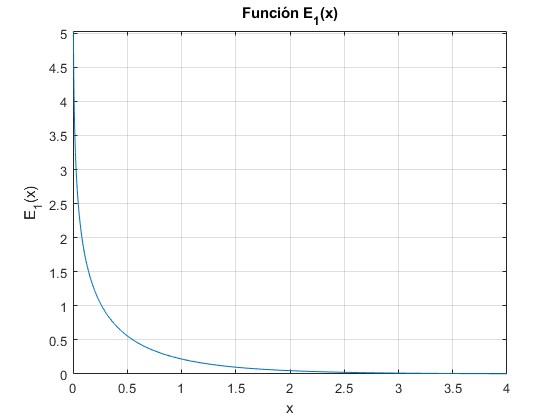
Una función similar es E₁(x)

${\displaystyle {\text{E}}_1\left(x\right)={\displaystyle \underset{x}{\overset{\infty }{\int }}\frac{e^{-t}}{t}dt}}$

fplot(@(x) expint(x),[0,4])
grid on
xlabel('x')
ylabel('E_1(x)')
title ('Función E_1(x)')

Movimiento de un cuerpo en una atmósfera no uniforme

La atmósfera isoterma es un buen modelo cuando un cuerpo de masa m se deja caer desde una altura z₀ de algunos kilómetros por encima de la superficie de la Tierra

${\displaystyle p=p_0\exp \left(-\frac{Mg}{RT}z\right)=p_0\exp \left(-\frac{z}{\lambda }\right),\lambda =\frac{RT}{Mg}}$

La ecuación del movimiento

${\displaystyle m\frac{d^{2}z}{d{t}^2}=mg-k_0{v}^2\exp \left(-\frac{z}{\lambda }\right)}$

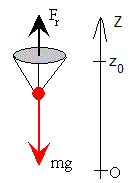
En vez de determinar la altura z en función del tiempo t, determinamos la velocidad de caída v en función de la altura z

${\displaystyle \begin{array}{l}\frac{d^{2}z}{d{t}^2}=\frac{dv}{dt}=\frac{dv}{dz}\frac{dz}{dt}=v\frac{dv}{dz}\\ v\frac{dv}{dz}=g\left(1-\frac{k_0}{mg}{v}^2\exp \left(-\frac{z}{\lambda }\right)\right)\end{array}}$

El cuerpo parte del reposo, incrementa su velocidad a medida que cae, alcanzando un valor límite constante dv/dz=0 cuando z se hace grande

${\displaystyle \begin{array}{l}0=g\left(1-\frac{k_0}{mg}{v}^2\right)\\ v_t^2=\frac{mg}{k_0}\end{array}}$

v_t es la velocidad límite constante

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}u=\frac{k_0}{mg}{v}^2={\left(\frac{v}{v_t}\right)}^2\\ x=\exp \left(-\frac{z}{\lambda }\right),z=-\lambda \ln x,dz=-\lambda \frac{dx}{x}\\ \frac{1}{2}\frac{d{v}^2}{dz}=g\left(1-\frac{k_0}{mg}{v}^2\exp \left(-\frac{z}{\lambda }\right)\right)\\ \frac{v_t^2}{2}\frac{du}{-\lambda \frac{dx}{x}}=g\left(1-ux\right)\\ \frac{du}{dx}=\frac{2\lambda g}{v_t^2}\left(\frac{1}{x}-u\right)\\ \frac{du}{dx}+au=\frac{a}{x},a=\frac{2\lambda g}{v_t^2}\end{array}}$

Solución de la ecuación diferencial

Para obtener la solución de esta ecuación diferencial seguimos los pasos que se describen en la página titulada Ecuaciones diferenciales (I) en el apartado titulado 'Ecuaciones diferenciales exactas'

Para utilizar la misma nomenclatura, cambiamos temporalmente el nombre de la variable u por t

${\displaystyle \begin{array}{l}dt+a\left(t-\frac{1}{x}\right)dx=\mathrm{0,}\{\begin{array}{l}P(t,x)=1\\ Q(t,x)=a\left(t-\frac{1}{x}\right)\end{array}\\ \frac{\partial P}{\partial x}\ne \frac{\partial Q}{\partial t}\end{array}}$

No es diferencial exacta, por lo que es posible encontrar un factor integrante μ tal que

${\displaystyle \frac{\partial }{\partial x}\left(\mu P\right)=\frac{\partial }{\partial t}\left(\mu Q\right)}$

Buscamos el factor integrante de la segunda forma de las dos posibles

${\displaystyle \begin{array}{l}\frac{1}{P}\left(\frac{\partial Q}{\partial t}-\frac{\partial P}{\partial x}\right)=g(x),\mu =\exp \left({\displaystyle \int g(x)dx}\right)\\ \frac{1}{1}\left(a-0\right)=g(x),\mu =\exp \left(ax\right)\end{array}}$

Comprobamos

${\displaystyle \begin{array}{l}\frac{\partial }{\partial x}\left(e^{ax}·1\right)=\frac{\partial }{\partial t}\left(e^{ax}a\left(t-\frac{1}{x}\right)\right)\\ a{e}^{ax}=a{e}^{ax}\end{array}}$

La ecuación diferencial se puede escribir de la forma

${\displaystyle \begin{array}{l}dU(t,x)=\mu P(t,x)dt+\mu Q(t,x)dx=0\hfill \\ \mu P(t,x)=\frac{\partial U}{\partial t},\mu Q(t,x)=\frac{\partial U}{\partial x}\hfill \end{array}}$

Integramos

${\displaystyle \begin{array}{l}U={\displaystyle \int \mu P(t,x)dt+\phi (x)}\hfill \\ \begin{array}{l}U={\displaystyle \int e^{ax}dt+\phi (x)}\\ U=t{e}^{ax}+\phi (x)\end{array}\hfill \end{array}}$

Obtenemos la función φ(x)

${\displaystyle \begin{array}{l}\mu Q(t,x)=\frac{\partial U}{\partial x}\\ e^{ax}a\left(t-\frac{1}{x}\right)=at{e}^{ax}+\frac{d\phi }{dx}\\ \frac{d\phi }{dx}=-a\frac{e^{ax}}{x}\\ \phi (x)=-a{\displaystyle \int \frac{e^{ax}}{x}dx}\\ U=t{e}^{ax}-a{\displaystyle \int \frac{e^{ax}}{x}dx}=c\\ t{e}^{ax}-a{\displaystyle \int \frac{e^{ax}}{x}dx}=c\end{array}}$

Donde c es una constante que se determina a partir de la condición inicial. Restauramos el nombre de la variable cambiando de t a u

${\displaystyle u=c{e}^{-ax}\text{+}a{e}^{-ax}{\displaystyle \int \frac{e^{ax}}{x}dx}}$

La condición inicial es u=0 para x=x₀, (el cuerpo parte desde la altura z₀ en reposo) por lo que c=0

Velocidad en función de la altura

En términos de las variables velocidad v y altura z, se escribe

${\displaystyle \begin{array}{l}{\left(\frac{v}{v_t}\right)}^2=a{e}^{-ax}{\displaystyle \underset{x_0}{\overset{x}{\int }}\frac{e^{ax}}{x}dx},x=\exp \left(-\frac{z}{\lambda }\right)\\ {\left(\frac{v}{v_t}\right)}^2=a{e}^{-ax}{\displaystyle \underset{a{x}_0}{\overset{ax}{\int }}\frac{e^t}{t}dt}\\ {\left(\frac{v}{v_t}\right)}^2=a{e}^{-ax}\left(\text{Ei}\left(ax\right)-\text{Ei}\left(a{x}_0\right)\right)\end{array}}$

Representamos el cociente de la velocidad adimensional v/v_t en términos de la variable adimensional t=1-z/z₀. El punto de partida es t=0, y el de llegada t=1. Los datos son

• Parámetro, λ=7.4621·10³
• Velocidad límite constante, v_t= 40 m/s

El coeficiente a vale

${\displaystyle a=\frac{2\lambda g}{v_t^2}=\text{91}\text{.4107}}$

lambda=7.4621e3;
a=2*lambda*9.8/40^2;
hold on
for z0=(10:10:30)*1000
    f=@(t) sqrt(a*exp(-a*exp(-(z0*(1-t)/lambda))).* 
(ei(a*exp(-z0*(1-t)/lambda))-ei(a*exp(-z0/lambda)))); 
    fplot(f,[0,1])
  %máximo
    x0=exp(-z0/lambda);
    g=@(x) a*x*exp(-a*x)*(ei(a*x)-ei(a*x0))-1;
    x_m=fzero(g,[x0,1]);
    z_m=-lambda*log(x_m);
    t_m=1-z_m/z0;
    line([t_m,t_m],[0,f(t_m)],'lineStyle','--')
end
hold off
grid on
xlabel('1-z/z_0')
ylabel('v/v_t')
title('Velocidad')

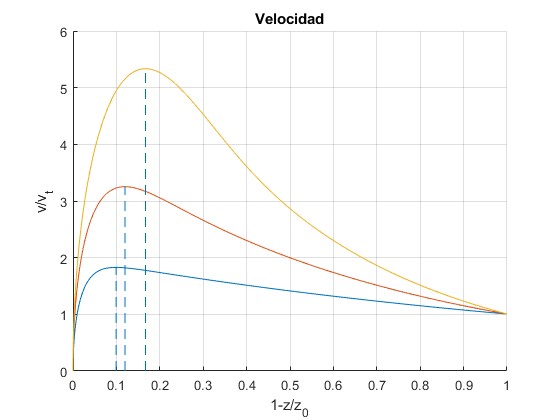
Observamos que la velocidad se incremente alcanzando un máximo a cierta altura y luego, disminuye hasta alcanzar una velocidad próxima a la límite v_t. Este comportamiento del cuerpo que cae, es distinto si la atmósfera es uniforme. En este caso, la velocidad se va incrementando hasta alcanzar una velocidad próxima a la limite constante

El máximo ocurre cuando dv/dz=0

${\displaystyle \begin{array}{l}mg=k_0{v}^2\exp \left(-\frac{z}{\lambda }\right)\\ \frac{mg}{k_0{v}_m^2}=\exp \left(-\frac{z_m}{\lambda }\right)\\ \frac{1}{u_m}=x_m\end{array}}$

Resolvemos la ecuación transcendente en x_m, la altura a la que se produce el máximo

${\displaystyle \begin{array}{l}{u}_m=a{e}^{-a{x}_m}\left(\text{Ei}\left(a{x}_m\right)-\text{Ei}\left(a{x}_0\right)\right)\\ \frac{1}{x_m}=a{e}^{-a{x}_m}\left(\text{Ei}\left(a{x}_m\right)-\text{Ei}\left(a{x}_0\right)\right)\end{array}}$

En la figura, se ha señalado el máximo con una línea a trazos

La función integral exponencial Ei(x) en otras páginas

• Movimiento vertical de un cohete con rozamiento (II)

• Evaporación de una gota

Referencias

Pirooz Mohazzabi. High-altitude free fall. Am J. Phys. 64 (10) October 1996, pp. 1242-1246