Polinomios ortogonales

Un conjunto de funciones φ₀(x), φ₁(x),....φ_n(x) continuas en [a,b] se denominan ortogonales, si

${\displaystyle {\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_j(x)}·{\phi }_i(x)dx=\{\begin{array}{l}0\text{si}i\ne j\\ C_i\text{si}i=j\end{array}}$

donde C_i es un número positivo, i,j=0,1,2...n, y w(x) se denomina función peso

Vamos a ajustar una función f(x) a una combinación lineal de n polinomios ortogonales φ_k(x) en el intervalo [a,b].

Dada una función f(x) continua en [a,b], encontraremos el polinomio P_n(x) calculando los coeficientes a₀, a₁...a_n

${\displaystyle P_n(x)=a_0{\phi }_0(x)+a_1{\phi }_1(x)+\mathrm{...}+a_n{\phi }_n(x)}$

de modo que la integral

${\displaystyle E={\displaystyle \underset{a}{\overset{b}{\int }}w(x){\left(P_n(x)-f(x)\right)}^{2}dx}}$

sea mínima. Para calcular el mínimo, se deriva respecto a a₁, a₂...a_n+1

${\displaystyle \frac{\partial E}{\partial a_i}=0i=\mathrm{1,2,...}n+1}$

Obtenemos el siguiente sistema de n ecuaciones con n incógnitas

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{\partial E}{\partial a_0}=0\Rightarrow {\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_0(x)\left(a_0{\phi }_0(x)+a_1{\phi }_1(x)+\mathrm{...}+a_n{\phi }_n(x)-f(x)\right)}dx=0\\ \frac{1}{2}\frac{\partial E}{\partial a_1}=0\Rightarrow {\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_1(x)\left(a_0{\phi }_0(x)+a_1{\phi }_1(x)+\mathrm{...}+a_n{\phi }_n(x)-f(x)\right)}dx=0\\ \mathrm{...}\\ \frac{1}{2}\frac{\partial E}{\partial a_n}=0\Rightarrow {\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_n(x)\left(a_0{\phi }_0(x)+a_1{\phi }_1(x)+\mathrm{...}+a_n{\phi }_n(x)-f(x)\right)}dx=0\end{array}}$

o bien,

${\displaystyle \begin{array}{l}{a}_0{\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_0(x)·{\phi }_0(x)dx}+a_1{\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_0(x){\phi }_1(x)dx}+\mathrm{...}+a_n{\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_0(x){\phi }_n(x)dx}={\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_0(x)f(x)dx}\\ a_0{\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_1(x){\phi }_0(x)dx}+a_1{\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_1(x){\phi }_1(x)dx}+\mathrm{...}+a_n{\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_1(x){\phi }_n(x)dx}={\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_1(x)f(x)dx}\\ \mathrm{...}\\ a_0{\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_n(x){\phi }_0(x)dx}+a_1{\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_n(x){\phi }_1(x)dx}+\mathrm{...}+a_n{\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_n(x){\phi }_n(x)dx}={\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_n(x)f(x)dx}\end{array}}$

Teniendo en cuenta la ortogonalidad de las funciones φ_k(x). El sistema de ecuaciones se reduce considerablemente

${\displaystyle \begin{array}{l}{a}_0{C}_0={\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_0(x)f(x)dx}\\ a_1{C}_1={\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_1(x)f(x)dx}\\ \mathrm{...}\\ a_n{C}_n={\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_n(x)f(x)dx}\end{array}}$

donde

${\displaystyle C_k={\displaystyle \underset{a}{\overset{b}{\int }}w(x)·{\phi }_k^2(x)dx}k=\mathrm{0,1,2...}n}$

Consideraremos dos conjuntos de polinomios ortogonales: los polinomios de Legendre y los polinomios de Chebyshev

Aproximación a polinomios de Legendre

Los primeros polinomios de Legendre son

${\displaystyle \begin{array}{l}{\phi }_0(x)=1\\ {\phi }_1(x)=x\\ {\phi }_2(x)=\frac{1}{2}\left(3x^2-1\right)\\ {\phi }_3(x)=\frac{1}{2}\left(5x^3-3x\right)\\ {\phi }_4(x)=\frac{1}{8}\left(35x^4-30x^2+3\right)\\ {\phi }_5(x)=\frac{1}{8}\left(63x^5-70x^3+15x\right)\end{array}}$

Estos polinomios son ortogonales respecto al peso w(x)=1

${\displaystyle {\displaystyle \underset{-1}{\overset{1}{\int }}{\phi }_i(x){\phi }_j(x)dx}=\{\begin{array}{l}0i\ne j\\ C_j=\frac{2}{2j+1}i=j\end{array}}$

Aproximamos la función f(x) en el intervalo [-1,1] a la combinación lineal P_n(x) de polinomios de Legendre

${\displaystyle P_n(x)=a_0{\phi }_0(x)+a_1{\phi }_1(x)+\mathrm{...}+a_n{\phi }_n(x)}$

Los coeficientes a_k se calculan del siguiente modo

${\displaystyle \begin{array}{l}{a}_k=\frac{1}{C_k}{\displaystyle \underset{-1}{\overset{1}{\int }}f(x){\phi }_k(x)dx}\\ C_k=\frac{2}{2k+1}k=\mathrm{0,1,2...}n\end{array}}$

Ejemplo 1

Aproximamos la función f(x)=exp(x) al polinomio P₃(x)

${\displaystyle P_3(x)=a_0{\phi }_0(x)+a_1{\phi }_1(x)+a_2{\phi }_2(x)+a_3{\phi }_3(x)}$

Integrando por partes, o con la ayuda de Math Symbolic, calculamos los coeficientes a₀, a₁, a₂ y a₃

${\displaystyle \begin{array}{l}{a}_0=\frac{1}{2}{\displaystyle \underset{-1}{\overset{1}{\int }}{e}^{x}dx=\frac{1}{2}\left(e-\frac{1}{e}\right)}\\ a_1=\frac{3}{2}{\displaystyle \underset{-1}{\overset{1}{\int }}x{e}^{x}dx=\frac{3}{e}}\\ a_2=\frac{5}{2}{\displaystyle \underset{-1}{\overset{1}{\int }}\frac{1}{2}\left(3x^2-1\right)e^{x}dx=\frac{5}{2}}\left(e-\frac{7}{e}\right)\\ a_3=\frac{7}{2}{\displaystyle \underset{-1}{\overset{1}{\int }}\frac{1}{2}\left(5x^3-3x\right)e^{x}dx=\frac{1}{2}}\left(\frac{259}{e}-35e\right)\end{array}}$

El polinomio P₃(x) es

${\displaystyle P_3(x)=\frac{1}{2}\left(e-\frac{1}{e}\right){\phi }_0(x)+\frac{3}{e}{\phi }_1(x)+\frac{5}{2}\left(e-\frac{7}{e}\right){\phi }_2(x)+\frac{1}{2}\left(\frac{259}{e}-35e\right){\phi }_3(x)}$

e=exp(1);
p=@(x) (e-1/e)/2+3*x/e+(5*(e-7/e)/2)*(3*x^2-1)/2+(259/e-35*e)*(5*x^3-3*x)/4;
hold on
fplot(@exp,[-1,1]);
fplot(p,[-1,1])
hold off
legend('exponencial','Legendre','location','northwest')
grid on
xlabel('x')
ylabel('y')
title('Aproximando exp(x) a un polinomio')

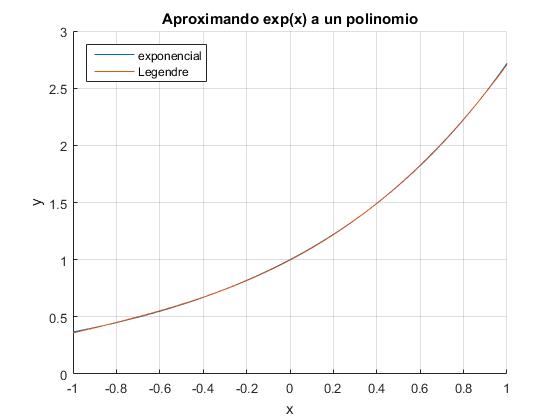
Elaboramos un script que nos permite aproximar la función e^x en el intervalo [-1,1] a una combinación P_n(x) de polinomios de Legendre. Sea n=3

syms x;
n=3;
pol=int(exp(x),x,-1,1)/2;
for k=1:n
    p=legendreP(k, x);
    a=int(p*exp(x),x,-1,1)*(2*k+1)/2;
    pol=pol+p*a;
end
hold on
fplot(@(x) exp(x),[-1,1]);
fplot(pol,[-1,1]);
legend('exponencial','Legendre','location','northwest')
hold off
grid on
xlabel('x')
ylabel('y')
title('Aproximación de e^x')

El polinomio P₃(x) ordenado en potencias de x es

>> collect(pol)
ans =((1295*exp(-1))/4 - (175*exp(1))/4)*x^3 + ((15*exp(1))/4 -
 (105*exp(-1))/4)*x^2 + ((105*exp(1))/4 - (765*exp(-1))/4)*x
 + (33*exp(-1))/4 - (3*exp(1))/4

Ejemplo 2

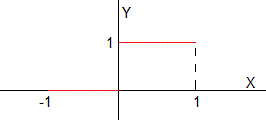
Aproximamos la función escalón f(x) al polinomio P₅(x)

${\displaystyle f(x)=\{\begin{array}{l}0-1<x<0\\ 10<x<1\end{array}}$

Calculamos los coeficientes a₀, a₁, a₂, a₃, a₄ y a₅

${\displaystyle \begin{array}{l}{a}_0=\frac{1}{2}{\displaystyle \underset{0}{\overset{1}{\int }}1·dx}=\frac{1}{2}\\ a_1=\frac{3}{2}{\displaystyle \underset{0}{\overset{1}{\int }}x·dx}=\frac{3}{4}\\ a_2=\frac{5}{2}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1}{2}\left(3x^2-1\right)·dx}=0\\ a_3=\frac{7}{2}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1}{2}\left(5x^3-3x\right)·dx}=-\frac{7}{16}\\ a_4=\frac{9}{2}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1}{8}\left(35x^4-30x^2+3\right)·dx}=0\\ a_5=\frac{11}{2}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1}{8}\left(63x^5-70x^3+15x\right)·dx}=\frac{11}{32}\end{array}}$

El polinomio P₅(x) es

${\displaystyle P_5(x)=\frac{1}{2}{\phi }_0(x)+\frac{3}{4}{\phi }_1(x)-\frac{7}{16}{\phi }_3(x)+\frac{11}{32}{\phi }_5(x)}$

syms x;
n=5;
pol=1/2;
for k=1:n
    p=legendreP(k,x);
    a=int(p,x,0,1)*(2*k+1)/2;
    pol=pol+p*a;
end
hold on
line([0,1],[1,1]);
line([-1,0],[0,0])
fplot(pol,[-1,1],'color','r');
hold off
grid on
xlabel('x')
ylabel('y')
title('Aproximación de f(x)')

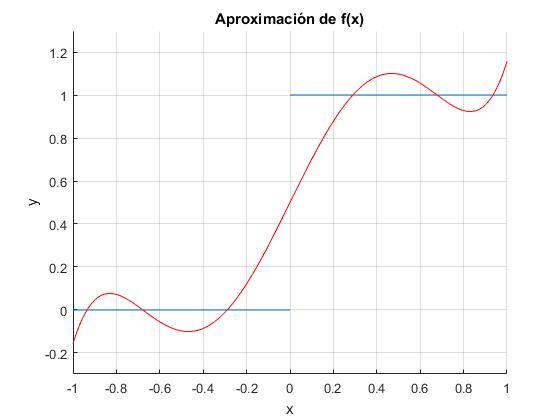
>> collect(pol)
ans =(693*x^5)/256 - (525*x^3)/128 + (525*x)/256 + 1/2

Ejemplo 3

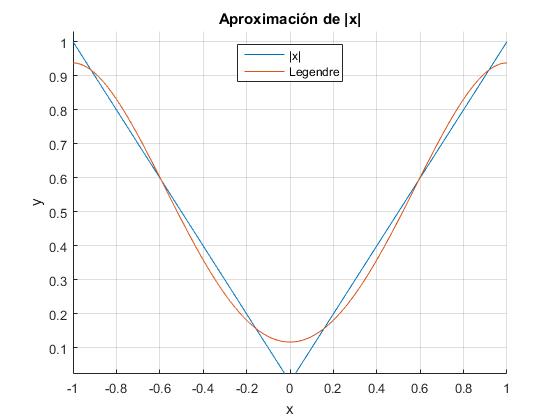
Aproximamos la función f(x)=|x| al polinomio P₄(x) en el intervalo [-1,1]

syms x;
n=4;
pol=int(abs(x),x,-1,1)/2;
for k=1:n
    p=legendreP(k,x);
    a=int(p*abs(x),x,-1,1)*(2*k+1)/2;
    pol=pol+p*a;
end
hold on
fplot(abs(x),[-1,1]);
fplot(pol,[-1,1]);
legend('|x|','Legendre','location','north')
hold off
grid on
xlabel('x')
ylabel('y')
title('Aproximación de |x|')

El polinomio P₄(x) ordenado en potencias de x es

>> collect(pol)
ans =- (105*x^4)/128 + (105*x^2)/64 + 15/128

Aproximación a polinomios de Chebyshev

Las funciones base φ_k(x), son los polinomios de Chebyshev T_k(x)

${\displaystyle \begin{array}{l}{T}_0(x)=1\\ T_1(x)=x\\ T_2(x)=2x^2-1\\ T_3(x)=4x^3-3x\\ T_4(x)=8x^4-8x^2+1\\ T_5(x)=16x^5-20x^3+5x\end{array}}$

Los polinomios son ortogonales respecto al peso

${\displaystyle \begin{array}{l}w(x)=\frac{1}{\sqrt{1-x^2}}\\ {\displaystyle \underset{-1}{\overset{1}{\int }}\frac{1}{\sqrt{1-x^2}}{T}_i(x)}{T}_j(x)dx=\{\begin{array}{l}0i\ne j\\ \pi i=j=0\\ \frac{\pi }{2}i=j\ne 0\end{array}\end{array}}$

Aproximamos la función f(x) en el intervalo [-1,1] a la combinación lineal P_n(x) de polinomios de Chebyshev.

${\displaystyle P_n(x)=a_0{T}_0(x)+a_1{T}_1(x)+\mathrm{...}+a_n{T}_n(x)}$

Los coeficientes a_k se calculan mediante la fórmula

${\displaystyle \begin{array}{l}{a}_k=\frac{1}{C_k}{\displaystyle \underset{-1}{\overset{1}{\int }}\frac{f(x)}{\sqrt{1-x^2}}{T}_k(x)dx}\\ C_0=\pi C_k=\frac{\pi }{2}k=\mathrm{1,2...}n\end{array}}$

Ejemplo 1

Aproximamos una semicircunferencia de radio r=1 a una combinación lineal P₂(x) de polinomios de Chebyshev

${\displaystyle P_2(x)=a_0{T}_0(x)+a_1{T}_1(x)+a_2{T}_2(x)}$

La función que describe la semicircunferencia de radio r=1, es

${\displaystyle f(x)=\sqrt{1-x^2}}$

Los coeficientes a_k se calculan del siguiente modo

${\displaystyle \begin{array}{l}{a}_0=\frac{1}{\pi }{\displaystyle \underset{-1}{\overset{1}{\int }}dx=}\frac{2}{\pi }\\ a_1=\frac{2}{\pi }{\displaystyle \underset{-1}{\overset{1}{\int }}xdx=0}\\ a_2=\frac{2}{\pi }{\displaystyle \underset{-1}{\overset{1}{\int }}\left(2x^2-1\right)dx=-\frac{4}{3\pi }}\\ P_2(x)=\frac{2}{\pi }-\frac{4}{3\pi }\left(2x^2-1\right)\end{array}}$

p=@(x) 2/pi-4*(2*x.^2-1)/(3*pi);
f=@(x) sqrt(1-x.^2);
hold on
fplot(f,[-1,1]);
fplot(p,[-1,1])
hold off
legend('semicircunferencia','Chebyshev','location','northwest')
grid on
axis equal
xlabel('x')
ylabel('y')
title('Aproximando f(x) a un polinomio')

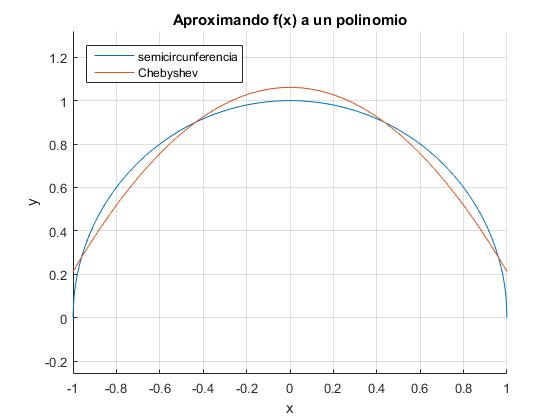
El lector interesado puede calcular a mano o con ayuda de Math Symbolic los coeficientes a₃=0, a₄..., para obtener mejores aproximaciones

Ejemplo 2

Aproximamos la función escalón f(x) al polinomio P₅(x)

${\displaystyle f(x)=\{\begin{array}{l}0-1<x<0\\ 10<x<1\end{array}}$

Calculamos los coeficientes a₀, a₁, a₂, a₃, a₄ y a₅

${\displaystyle a_k=\frac{1}{C_k}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{T_k(x)}{\sqrt{1-x^2}}dx}}$

A partir de la definición de polinomio de Chebyshev T_k(θ)=cos(kθ) y haciendo el cambio de variable x=cos(θ) los coeficientes a_k se calculan del siguiente modo

${\displaystyle \begin{array}{l}{a}_0=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}d\theta }=\frac{1}{2}\\ a_k=\frac{2}{\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \left(k\theta \right)d\theta }\end{array}}$

syms x;
for k=1:5
    f=cos(k*x);
    int(f,x,0,pi/2)*2/pi  
end

ans =2/pi
ans =0
ans =-2/(3*pi)
ans =0
ans =2/(5*pi)

El polinomio P₅(x) es

${\displaystyle P_5(x)=\frac{1}{2}{\phi }_0(x)+\frac{2}{\pi }{\phi }_1(x)-\frac{2}{3\pi }{\phi }_3(x)+\frac{2}{5\pi }{\phi }_5(x)}$

syms x;
n=5;
pol=1/2;
for k=1:n
    f=cos(k*x);
    a=int(f,x,0,pi/2)*2/pi;
    pol=pol+a*chebyshevT(k,x);   
end
hold on
line([0,1],[1,1]);
line([-1,0],[0,0])
fplot(pol,[-1,1],'color','r');
hold off
grid on
xlabel('x')
ylabel('y')
title('Aproximación de f(x)')

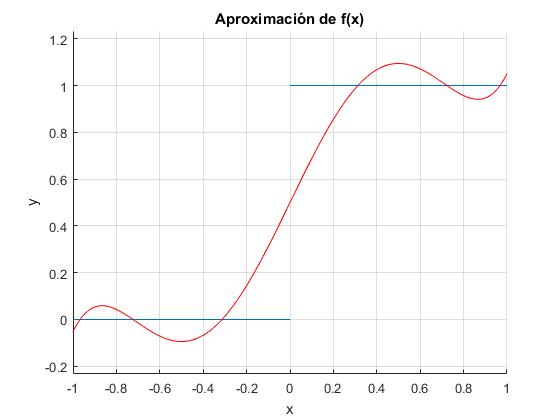
>> collect(pol)
ans =(32*x^5)/(5*pi) - (32*x^3)/(3*pi) + (6*x)/pi + 1/2

Ejemplo 3

Aproximamos la función f(x)=exp(x) en el intervalo [-1,1], mediante la combinación lineal P₃(x) de polinomios de Chebyshev,

${\displaystyle P_3(x)=a_0{T}_0(x)+a_1{T}_1(x)+a_2{T}_2(x)+a_3{T}_3(x)}$

Para calcular los coeficientes a_k, observamos que el integrando diverge en los extremos del intervalo [-1,1]. La integración numérica en términos de la variable x no parece la más apropiada. A partir de la definición de polinomio de Chebyshev T_k(θ)=cos(kθ) y haciendo el cambio de variable x=cos(θ) los coeficientes a_k se escriben

${\displaystyle \begin{array}{l}{a}_0=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\exp \left(\cos \theta \right)·d\theta }\\ a_k=\frac{2}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\exp \left(\cos \theta \right)·\cos \left(k\theta \right)·d\theta }k=\mathrm{1,2...}n\end{array}}$

Llevamos a cabo la integración numérica, mediante la función MATLAB, integral

>> f=@(x) exp(cos(x));
>> integral(f,0,pi)/pi
ans =    1.2661
>> f=@(x) exp(cos(x)).*cos(x);
>> 2*integral(f,0,pi)/pi
ans =    1.1303
>> f=@(x) exp(cos(x)).*cos(2*x);
>> 2*integral(f,0,pi)/pi
ans =    0.2715
>> f=@(x) exp(cos(x)).*cos(3*x);
>> 2*integral(f,0,pi)/pi
ans =    0.0443

El polinomio aproximador es
P₃(x)=1.2661·T₀(x)+1.1303·T₁(x)+0.2715·T₂(x)+0.0443·T₃(x)

P₃(x)=1.2661+1.1303·x+0.2715·(2x²-1)+0.0443·(4x³-3x)

p=@(x) 1.2661+1.1303*x+0.2715*(2*x.^2-1)+0.0443*(4*x.^3-3*x);
hold on
fplot(@exp,[-1,1]);
fplot(p,[-1,1])
hold off
legend('exponencial','Chebyshev','location','northwest')
grid on
xlabel('x')
ylabel('y')
title('Aproximando e^x a un polinomio')

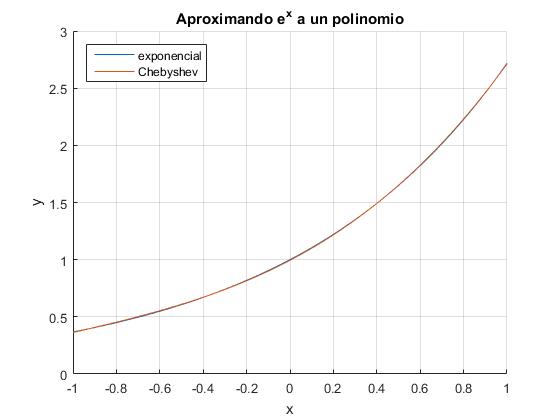
Elaboramos un script que nos permita aproximar la función e^x a P_n(x) en el intervalo [-1,1]. Sea por ejemplo, n=3

n=3;
f=@(x) exp(cos(x));
pol=integral(f,0,pi)/pi; %a_0
for k=1:n
    f=@(x) exp(cos(x)).*cos(k*x);
    a=integral(f,0,pi)*2/pi;   %a_k
    pol=pol+chebyshevT(k,x)*a;
end
hold on
fplot(exp(x),[-1,1]);
fplot(pol,[-1,1]);
legend('exponencial','Chebyshev','location','northwest')
hold off
grid on
xlabel('x')
ylabel('y')
title('Aproximación de e^x')