Un motor y generador eléctrico en forma de disco
El motor eléctrico
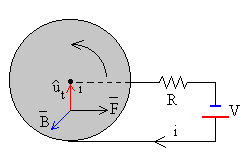
Como se ve en la figura, la batería produce una corriente que va del borde del disco al centro. El campo magnético ejerce una fuerza, que produce un momento que hace girar el disco en sentido antihorario.
Ecuación del movimiento
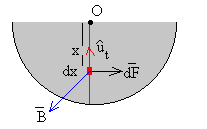
La fuerza sobre un elemento de corriente dx situado a una distancia x del eje del disco es
Su módulo es dF=iB·dx y está dirigido como vemos en la figura hacia la derecha.
El momento de esta fuerza respecto del eje del disco es dM=x·dF, y el momento total
La fuerza resultante F=iBa que produce un momento total M estará aplicada en el punto medio del radio, a/2 tal como se muestra en la primera figura.
La ecuación de la dinámica de rotación del disco alrededor de su eje fijo es I0α =M
(1)
donde I0 es el momento de inercia que calculamos mediante la fórmula I0=ma2/2, donde m es la masa del disco y a su radio.
Ecuación del circuito
Como hemos explicado al calcular la fem en la dinamo de disco, al girar el disco se produce una corriente inducida cuyo sentido es contrario al de la corriente de la batería.
La fuerza sobre los portadores de carga es
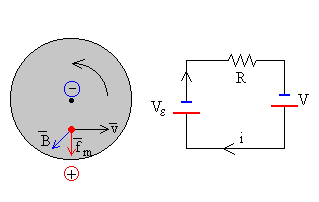
La fuerza por unidad de carga En=fm/q=v·B=ωBx,
Su dirección es radial y su sentido va del centro a la periferia. Las cargas positivas son impulsadas por la fuerza fm desde el centro hacia la periferia.
Se define la fem como la integral
La ecuación del circuito se puede formular fácilmente a partir del esquema de la figura (derecha) como: suma de fems igual a intensidad por resistencia
(2)
De las ecuaciones (1) y (2) obtenemos la expresión de la velocidad angular ω del disco en función del tiempo, y de la intensidad i en función del tiempo.
Cuya solución con las condiciones iniciales t=0, ω =0, es
Como vemos la velocidad angular del disco crece desde cero hasta un valor máximo dado por 2V/(Ba2) y es independiente de la resistencia R. La resistencia determina el tiempo (la inversa de b) que tarda el disco en alcanzar dicha velocidad máxima.
La intensidad decrece exponencialmente con el tiempo. En la ecuación del circuito, la intensidad es la diferencia de dos términos, la producida por la batería que es constante e igual a V/R, y la intensidad de la corriente inducida que se opone a ésta y crece desde cero hasta que alcanza el valor límite constante V/R. Estos dos términos los representamos en la parte inferior derecha del programa interactivo, al final de esta página.
Balance energético
La energía cinética del disco en cualquier instante t es
La energía suministrada por la batería en la unidad de tiempo (potencia) es V·i, y en el tiempo t es
La energía disipada en la resistencia R en la unidad de tiempo es i2·R, y en el tiempo t es
Comprobamos que Ek+ER=EV, parte de la energía suministrada por la batería se invierte en energía cinética del disco y la otra parte, se disipa en la resistencia.
En la parte superior derecha del programa interactivo, un círculo representa la energía suministrada por la batería que está dividido en dos sectores el de color azul representa la energía cinética del disco y el de color negro la parte disipada en la resistencia.
Al cabo de un cierto tiempo, teóricamente infinito pero que en la práctica depende de la constante de tiempo (inversa de b) la energía suministrada por la batería EV tiende a un valor constante, y se divide en dos partes iguales, la mitad como energía cinética del disco Ek (gira con velocidad constante) y la otra mitad se disipa en la resistencia ER.
El generador eléctrico
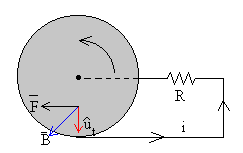
Una vez alcanzada un valor próximo a la velocidad angular límite constante, desconectamos la batería, vamos a ver que el disco se frena debido al momento de la fuerza que ejerce el campo magnético sobre la corriente inducida.
Ecuación del circuito
El sentido de la fem Vε no cambia, por tanto, la corriente i circula ahora en sentido horario y vale (2)
Ecuación del movimiento
La ecuación del circuito junto a la ecuación del movimiento (1), nos da la expresión de la velocidad angular y de la intensidad en función del tiempo.
La solución de esta ecuación con las condiciones iniciales t=0, ω =ω0 es
La velocidad angular del disco disminuye exponencialmente con el tiempo, la intensidad de la corriente inducida tiene el mismo comportamiento
Balance energético
La energía cinética inicial
La energía cinética en cualquier instante
La energía disipada en la resistencia durante un tiempo t.
La energía cinética que pierde el disco se disipa en la resistencia.
Después de un tiempo, teóricamente infinito, toda la energía cinética inicial del disco se disipa en la resistencia en forma de calor.
Actividades
El lector puede estudiar el comportamiento del disco y predecir el sentido del momento que ejerce el campo magnético sobre la corriente que circula entre el centro del disco y la periferia del mismo y el sentido de la corriente inducida, en las siguientes casos:
- Fem V de la batería positiva
- Campo magnético B positivo
- Campo magnético B negativo
- Fem V de la batería negativa
- Campo magnético B positivo
- Campo magnético B negativo
Se introduce
- el campo magnético (<10 T), en el control titulado Campo magnético
- la fem de la batería (<1 V), en el control titulado ddp batería
- la resistencia total del circuito (en ohm), en el control titulado Resistencia
Se pulsa el botón titulado Nuevo.
Comprobamos que la velocidad angular límite ω∞ viene dada por el cociente
El programa no responde adecuadamente si esta velocidad es elevada, es decir, si B es pequeño y/o V es grande.
Comprobamos que si la resistencia R es grande, el tiempo que se tarda en alcanzar aproximadamente la velocidad angular límite ω∞ es grande.
La ventana gráfica está dividida en tres partes.
A la izquierda, se observa el movimiento del disco, se representa el circuito, inicialmente con batería conectada y cuando se alcanza una velocidad angular aproximadamente constante, se desconecta la batería. Se representa mediante el movimiento de puntos de color rojo, el sentido de la corriente en el circuito, y la fuerza que el campo magnético ejerce sobre los portadores de carga.
- El campo magnético está representado por una flecha de color azul
- La velocidad de los portadores de carga por una flecha de color rojo
- La fuerza sobre dichos portadores, mediante una flecha de color negro.
En la parte superior derecha, se representa el balance energético.
- El círculo representa la energía suministrada por la batería, que se transforma en
- El sector azul representa la energía cinética del disco
- El sector negro, la energía disipada en la resistencia
Cuando se alcanza la velocidad angular máxima, la mitad de la energía
aportada por la batería se convierte en energía cinética de rotación del
disco y la otra mitad, se ha disipado en forma de calor en la resistencia.
Cuando se desconecta la batería, la energía cinética del disco va
disminuyendo a medida que se disipa en la resistencia. Finalmente, toda la
energía cinética inicial representado por un semicírculo (en el momento en
el que se desconecta la batería) se convierte en calor en la resistencia.
En la parte inferior derecha, se representa.
- la intensidad de la corriente producida por la batería en color azul.
- la intensidad de la corriente inducida, en color rojo.
La intensidad en el circuito es la suma de ambas intensidades.
Cuando se desconecta la batería la intensidad de la corriente producida por ésta se hace cero (la línea horizontal de color azul desaparece).

