Cañón electromagnético

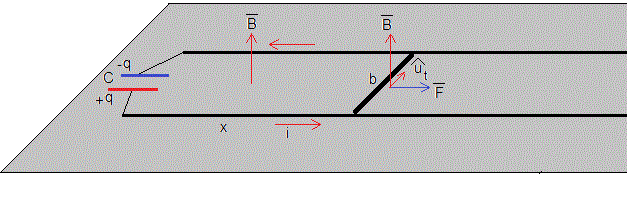
El cañón electromagnético consta de un banco de condensadores de capacidad C, inicialmente cargado con q₀. Se conectan a dos vías paralelas de aluminio de 4 m de longitud y r=1 cm de radio, separadas b=10 cm.

Se coloca una varilla deslizante de masa m=10 kg sobre las vías cerrando el circuito. La intensidad que circula por las vías produce un campo magnético perpendicular al plano del dispositivo. Este campo ejerce una fuerza sobre la corriente que pasa por la varilla, adquiriendo una velocidad muy elevada en décimas de segundo, como veremos en los cálculos al final de la página.

Ecuación del movimiento

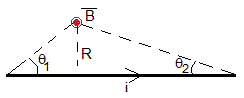
El campo magnético producido por un segmento rectilíneo de corriente, se ha calculado en la página titulada, Campo magnético producido por una corriente rectilínea indefinida

$B = \frac{μ_{0} i}{4 π R} (\cos θ_{1} + \cos θ_{2})$

cuya dirección es perpendicular al plano que contiene la corriente y el punto y cuyo sentido se determina aplicando la regla de la mano derecha.

Los campos magnéticos producidos por los segmentos rectilíneos de corriente horizontales sobre un punto (x,y) de la varilla deslizante (θ₂=90°), marcado en color rojo, son

$\begin{array}{l} B_{1} = \frac{μ_{0} i}{4 π y} \frac{x}{\sqrt{y^{2} + x^{2}}} \\ B_{2} = \frac{μ_{0} i}{4 π (b - y)} \frac{x}{\sqrt{{(b - y)}^{2} + x^{2}}} \end{array}$

Ambos tienen la misma dirección y sentido, B(y)=B₁+B₂.

Fuerza sobre la varilla deslizante

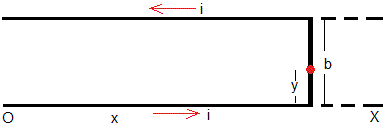
La fuerza $\vec{d F} = i ({\hat{u}}_{t} \times \vec{B}) d l$ que ejerce este campo sobre una porción diferencial dy de la corriente en la varilla deslizante, es

$d F = i \cdot B (y) d y$

Su dirección es el eje X y sentido hacia la derecha, (véase la primera figura). La fuerza total sobre la varilla deslizante es

$F (x) = \frac{μ_{0} i^{2}}{4 π} x \int_{r}^{b - r} {\frac{1}{y} \frac{1}{\sqrt{y^{2} + x^{2}}} + \frac{1}{(b - y)} \frac{1}{\sqrt{{(b - y)}^{2} + x^{2}}}} d y$

Siendo r el radio de las vías

Para resolver la integral, hacemos el cambio, y=xsinh(t)

$\int \frac{1}{y} \frac{1}{\sqrt{y^{2} + x^{2}}} d y = \frac{1}{x} \int \frac{d t}{\sinh t} = \frac{1}{x} \int \frac{d t}{2 \sinh (t / 2) \cosh (t / 2)} = \frac{1}{2 x} \int \frac{\frac{1}{\cosh^{2} (t / 2)}}{\tanh (t / 2)} d t = \frac{1}{x} \ln (\tanh (\frac{t}{2}))$

Teniendo en cuenta las relaciones

$\begin{array}{l} \cosh t = \cosh^{2} (\frac{t}{2}) + \sinh^{2} (\frac{t}{2}) \\ 1 = \cosh^{2} (\frac{t}{2}) - \sinh^{2} (\frac{t}{2}) \end{array}$

obtenemos

$\frac{1}{x} \ln (\tanh (\frac{t}{2})) = \frac{1}{x} \ln (\sqrt{\frac{\cosh t - 1}{\cosh t + 1}}) = \frac{1}{2 x} \ln (\frac{\cosh t - 1}{\cosh t + 1}) = \frac{1}{2 x} \ln (\frac{\sqrt{1 + \frac{y^{2}}{x^{2}}} - 1}{\sqrt{1 + \frac{y^{2}}{x^{2}}} + 1}) = \frac{1}{2 x} \ln (\frac{\sqrt{x^{2} + y^{2}} - x}{\sqrt{x^{2} + y^{2}} + x})$

Nos queda por calcular el segundo término de la expresión de la fuerza. Hacemos el cambio de variable u=b-y, du=-dy, una integral similar al anterior

$\int \frac{1}{(b - y)} \frac{1}{\sqrt{{(b - y)}^{2} + x^{2}}} d y = - \int \frac{1}{u} \frac{1}{\sqrt{u^{2} + x^{2}}} d u = - \frac{1}{2 x} \ln (\frac{\sqrt{x^{2} + u^{2}} - x}{\sqrt{x^{2} + u^{2}} + x}) = - \frac{1}{2 x} \ln (\frac{\sqrt{x^{2} + {(b - y)}^{2}} - x}{\sqrt{x^{2} + {(b - y)}^{2}} + x})$

La expresión de la fuerza sobre la varilla deslizante es

$\begin{array}{l} F (x) = \frac{μ_{0} i^{2}}{8 π} {\ln (\frac{\sqrt{x^{2} + y^{2}} - x}{\sqrt{x^{2} + y^{2}} + x}) - \ln (\frac{\sqrt{x^{2} + {(b - y)}^{2}} - x}{\sqrt{x^{2} + {(b - y)}^{2}} + x})}_{r}^{b - r} = \\ \frac{μ_{0} i^{2}}{4 π} {\ln (\frac{\sqrt{x^{2} + {(b - r)}^{2}} - x}{\sqrt{x^{2} + {(b - r)}^{2}} + x}) - \ln (\frac{\sqrt{x^{2} + r^{2}} - x}{\sqrt{x^{2} + r^{2}} + x})} = \\ \frac{μ_{0} i^{2}}{4 π} \ln {\frac{(\sqrt{x^{2} + {(b - r)}^{2}} - x) (\sqrt{x^{2} + r^{2}} + x)}{(\sqrt{x^{2} + {(b - r)}^{2}} + x) (\sqrt{x^{2} + r^{2}} - x)}} \end{array}$

La ecuación del movimiento es

$m \frac{d^{2} x}{d t^{2}} = F (x)$

Ecuación del circuito

El circuito está formado por un condensador de capacidad C, con una carga inicial q₀, una resistencia (las vías, la varilla deslizante y los cables de conexión) y una autoinducción, (la espira rectangular).

La resistencia es variable, ya que la longitud x de la espira rectangular aumenta

$R (x) = \frac{1}{σ} \frac{2 x + b}{π r^{2}}$

donde σ es la conductividad del material, 2x+b es la longitud del circuito (no se tiene en cuenta los cables de conexión al condensador) y r es el radio de las vías

En la página titulada Coeficiente de autoinducción hemos deducido la fórmula de la autoinducción de una espira rectangular de lados a y b. Supondremos que nuestro circuito es una espira rectangular de lados x y b

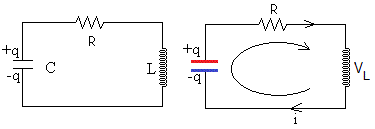
$L (x) \approx \frac{μ_{0}}{π} {x \cdot \log (\frac{2 x}{r}) + b \cdot \log (\frac{2 b}{r}) - x \log (\frac{x + \sqrt{x^{2} + b^{2}}}{b}) - b \log (\frac{b + \sqrt{x^{2} + b^{2}}}{x}) - 2 (x + b) + 2 \sqrt{x^{2} + b^{2}}}$

En la autoinducción, el flujo propio es Φ=Li. La fem es

$V_{L} = - \frac{d (L i)}{d t}$

donde el coeficiente de autoinducción L y la intensidad i cambian con el tiempo.

La ecuación del circuito es,

$\begin{array}{l} V_{L} + \frac{q}{C} = i R \\ (- \frac{d (L i)}{d t}) + \frac{q}{C} = i R, i = - \frac{d q}{d t} \end{array}$

La corriente i extrae carga de la placa positiva por lo que i=-dq/dt

La ecuación diferencial es

$L \frac{d^{2} q}{d t^{2}} + (R + \frac{d L}{d t}) \frac{d q}{d t} + \frac{q}{C} = 0$

Cuando el coeficiente de autoinducción L=0, obtenemos la ecuación de la descarga de un condensador a través de una resistencia
Cuando la resistencia R=0, y el coeficiente de autoinducción L es constante, obtenemos la ecuación de las oscilaciones eléctricas. Cuando R≠0, obtenemos la ecuación diferencial de las oscilaciones eléctricas amortiguadas

Solución numérica

La ecuación del movimiento y la ecuación del circuito, contituyen un sistema de dos ecuaciones diferneciales de segundo orden que se resuelven por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, x=0, v=0, (la varilla deslizante parte del origen en reposo). El condensador está cargado q=q₀ y la intensidad de la corriente en el circuito i=-dq/dt es nula

${\begin{cases} \frac{d^{2} x}{d t^{2}} = \frac{F (x)}{m} \\ \frac{d^{2} q}{d t^{2}} = - \frac{1}{L (x)} (R (x) + \frac{d L (x)}{d x} \frac{d x}{d t}) \frac{d q}{d t} - \frac{1}{L (x) \cdot C} q = 0 \end{cases}$

Nos queda por calcular la expresión de la derivada del coeficiente de autoinducción, dL/dx

$\frac{d L (x)}{d x} = \frac{μ_{0}}{π} {\ln (\frac{2 x}{r}) - 1 - \ln (\frac{x + \sqrt{x^{2} + b^{2}}}{b}) + \frac{\sqrt{x^{2} + b^{2}}}{x}}$

El último término, contiene x en el denominador y el primero, contiene ln(x). Si la posición inicial de varilla deslizante fuera x=0, se produciría un ln(0) y una división entre cero. Para evitarlo, cambiaremos la posición inicial de la varilla a x₀>0

Ejemplo

Masa de la varilla deslizante, m=10 kg
Longitud de las vías, 4 m
Radio de las vías, r= 1 cm
Distancia entre las dos vías paralelas, b=10 cm
Las vías son de aluminio de conductividad σ=37.8·10⁶ S/m
La capacidad del banco de condensadores, C=1500 F
Diferencia de potencial inicial, V₀=875 V

El procedimiento numérico ode45 se detiene cuando la posición de la varilla deslizante es 4.1 m. Como parte de x₀=0.1 m, se desplaza 4 m. Par ello definimos la función stop_railgun que pasamos al procedimiento ode45

function [value,isterminal,direction]=stop_railgun(t,x, a)
    value=x(1)-a;  
    isterminal=1;
    direction=1; 
end

El código completo del script es

m=10; %masa
C=1500; %capacidad
q0=875*C; %carga inicial
sigma=37.8e6; %conductividad del aluminio
b=0.1; %separación raíles paralelos
r=0.01; %radio de los raíles

%resistencia, autoinducción, derivada de L
R=@(x) (2*x+b)/(sigma*pi*r^2);
L=@(x) 4e-7*(-2*(x+b)+2*sqrt(x^2+b^2)-b*log((b+sqrt(b^2+x^2))/x)
-x*log((x+sqrt(b^2+x^2))/b)+b*log(2*b/r)+x*log(2*x/r));
dL=@(x) 4e-7*(log(2*x/r)-1-log((x+sqrt(x^2+b^2))/b)+sqrt(x^2+b^2)/x);

%x(1) es x, x(2) es dx/dt, x(3) es q, x(4) es dq/dt
opts=odeset('events',@(t,x) stop_railgun(t,x,4.1)); %Posición final
fg=@(t,x)[x(2);1e-7*x(4)^2*log((sqrt(x(1)^2+(b-r)^2)-x(1))*
(sqrt(x(1)^2+r^2)+x(1))/((sqrt(x(1)^2+(b-r)^2)+x(1))*
(sqrt(x(1)^2+r^2)-x(1))))/m ; x(4);-x(3)/(C*L(x(1)))-
x(4)*(R(x(1))+dL(x(1))*x(2))/L(x(1))];
[t,x]=ode45(fg,[0,0.1],[0.2,0,q0,0], opts);

plot(t,x(:,1)) %posición
grid on
xlabel('t')
ylabel('x')
title('Proyectil electromagnético. Posición')

Posición en función del tiempo

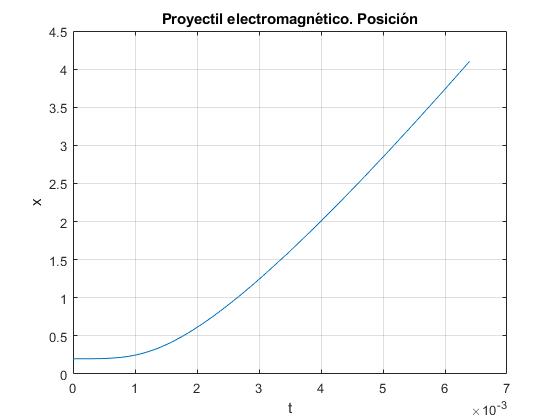
La varilla deslizante recorre 4 m en 6.4 ms

>> t(end)
ans =    0.0064

Velocidad en función del tiempo

Cambiamos la sentencia plot para representar la velocidad en función del tiempo

...
plot(t,x(:,2)) %velocidad
grid on
xlabel('t')
ylabel('v')
title('Proyectil electromagnético. velocidad')

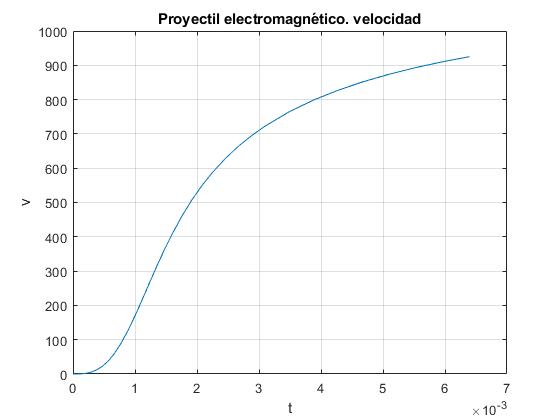
Carga del condensador en función del tiempo

Cambiamos la sentencia plot para representar la carga del condensador en función del tiempo

...
plot(t,x(:,3)) %carga
grid on
xlabel('t')
ylabel('q')
title('Proyectil electromagnético. Carga')

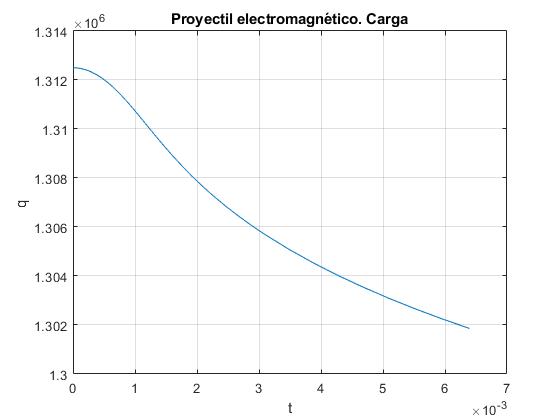
Intensidad de la corriente en función del tiempo

Cambiamos la sentencia plot para representar la intensidad i=-dq/dt de la corriente en función del tiempo

...
plot(t,-x(:,4)) %intensidad
grid on
xlabel('t')
ylabel('i')
title('Proyectil electromagnético. Intensidad')

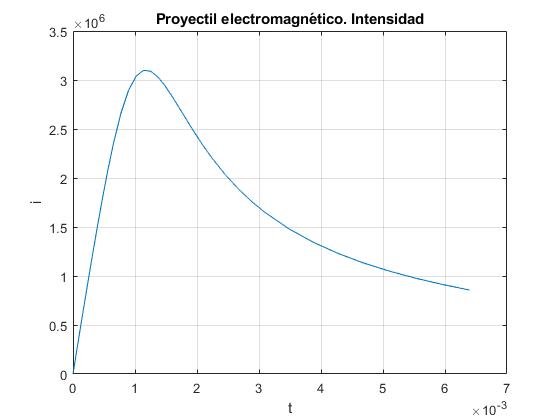
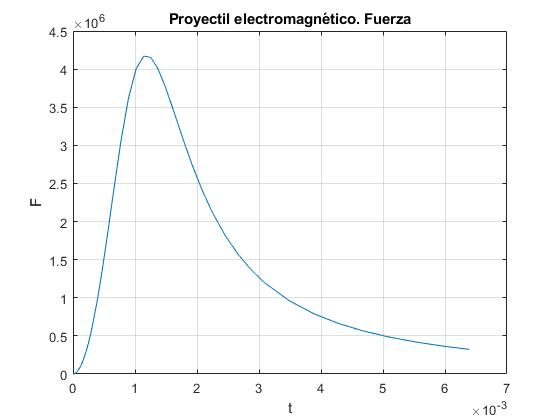
Fuerza en función del tiempo

Modificamos el script para representar la fuerza en función del tiempo

...
[t,x]=ode45(fg,[0,0.1],[0.2,0,q0,0], opts);

%x es posición, y es intensidad
F=@(x,y) 1e-7*(y.^2).*log(((sqrt(x.^2+(b-r)^2)-x).*(sqrt(x.^2+r^2)+x)).
/((sqrt(x.^2+(b-r)^2)+x).*(sqrt(x.^2+r^2)-x)));
FF=F(x(:,1),x(:,4));

plot(t,FF)
grid on
xlabel('t')
ylabel('F')
title('Proyectil electromagnético. Fuerza')

Referencias

Gabriel I. Font, Anthony N. Dills. Analyzing Railguns with Excel: Simple Numerical Integration for the Classroom. The Physics Teacher, Vol 56, October 2018, pp. 436-440