Acelerador de partículas cargadas. El ciclotrón
En esta página trataremos de visualizar la trayectoria seguida por un ión en un ciclotrón y conocer los factores de los que depende la energía final.
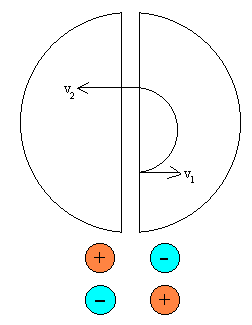
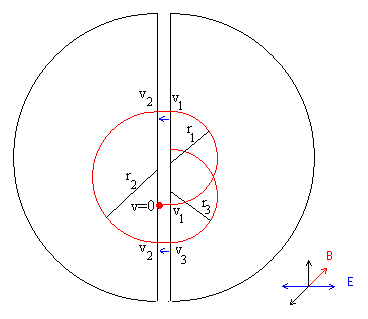
El ciclotrón consta de dos placas semicirculares huecas, que se montan con sus bordes diametrales adyacentes dentro de un campo magnético uniforme que es normal al plano de las placas y se hace el vacío. A dichas placas se le aplican oscilaciones de alta frecuencia que producen un campo eléctrico oscilante en la región diametral entre ambas.
Como consecuencia, durante un semiciclo el campo eléctrico acelera los iones, formados en la región diametral, hacia el interior de uno de los electrodos, llamados 'Ds', donde se les obliga a recorrer una trayectoria circular mediante un campo magnético y finalmente, aparecerán de nuevo en la región intermedia.
El campo magnético se ajusta de modo que el tiempo que se necesita para recorrer la trayectoria semicircular dentro del electrodo sea igual al semiperiodo de las oscilaciones. En consecuencia, cuando los iones vuelven a la región intermedia, el campo eléctrico habrá invertido su sentido y los iones recibirán entonces un segundo aumento de la velocidad al pasar al interior de la otra 'D'.
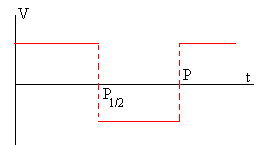
Como los radios de las trayectorias son proporcionales a las velocidades de los iones, el tiempo que se necesita para el recorrido de una trayectoria semicircular es independiente de sus velocidades. Por consiguiente, si los iones emplean exactamente medio ciclo P1/2 en una primera semicircunferencia, se comportarán de modo análogo en todas las sucesivas y por tanto, se moverán en espiral y en resonancia con el campo oscilante hasta que alcancen la periferia del aparato.
Su energía cinética final, será tantas veces mayor que la que corresponde al voltaje aplicado a los electrodos multiplicado por el número de veces que el ión ha pasado por la región intermedia entre las 'Ds'.
Movimiento circular
Una partícula cargada describe un arco de circunferencia en un campo magnético uniforme. La fuerza sobre la partícula viene dada por el producto vectorial . Su módulo es fm=qvB, su dirección radial y su sentido hacia el centro de la circunferencia
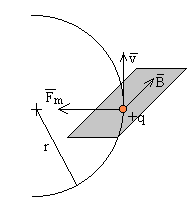
Aplicando la segunda ley de Newton al movimiento circular uniforme, obtenemos el radio de la circunferencia.
El tiempo que tarda en describir una semicircunferencia es por tanto, independiente del radio r de la órbita
Aceleración del ión

El ión es acelerado por el campo eléctrico existente entre las D's. Incrementa su energía cinética en una cantidad igual al producto de su carga por la diferencia de potencial existente entre las D's.
Cuando el ión completa una semicircunferencia en el tiempo constante P1/2, se invierte la polaridad por lo que es nuevamente acelerado por el campo existente en la región intermedia. De nuevo, incrementa su energía cinética en una cantidad igual al producto de su carga por la diferencia de potencial existente entre las D's.
La energía final del ión es nqV, siendo n el número de veces que pasa por la región entre las D's.
Ejemplo
- Se elige como partícula el protón, m=1.67·10-27 kg
- Campo magnético, B=60 gauss=60·10-4 T
- Diferencia de potencial entre las D's, V=100 V
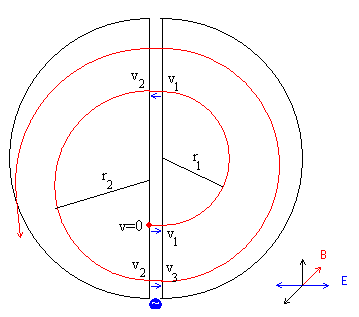
- El ión parte del reposo y se acelera por la diferencia de potencial existente entre las dos D's
- La partícula describe una trayectoria semicircular de radio r1
- La diferencia de potencial alterna cambia de polaridad y la partícula se acelera
- La partícula describe una trayectoria semicircular de radio r2
- y así, sucesivamente...
La energía final de la partícula cuando sale del ciclotrón es Ek=4·qV=4·1.6·10-19·100 J=400 eV, ya que es acelerada cuatro veces al pasar por la región comprendida entre las dos D's
Actividades
Se selecciona el ión que se va a acelerar, en el control titulado Partículas .
Se introduce
- la intensidad del campo magnético (en gauss=10-4 T), en el control titulado Campo magnético
- la diferencia de potencial (en volts) entre las 'Ds', en el control titulado Diferencia de potencial
Se pulsa en el botón Nuevo,
Se dibuja la trayectoria del ión en forma de espiral. Una flecha indica el final de la trayectoria dentro del ciclotrón, su dirección es tangente a su trayectoria circular.
En la parte derecha, se muestra la energía final de la partícula en electrón voltios. Para obtener este valor se multiplica el número de veces n que el ión pasa por la región intermedia entre las D's por la diferencia de potencial V entre dichos electrodos y por la carga q del ión.
- Probar con distintos valores de la diferencia de potencial manteniendo constante la intensidad del campo magnético.
- Mantener constante la diferencia de potencial, modificando la intensidad del campo magnético
- Por último, cambiar el tipo de partícula.
Frecuencia de resonancia del ciclotrón
Ahora analizamos el papel del periodo de la fem alterna conectada a las dos D's. En el apartado anterior, el semiperiodo de la fem alterna coincidía con el tiempo que tarda el ión en describir una semicircunferencia que es independiente de su radio r
Vamos a ver cómo cambia la trayectoria del ión cuando estos dos tiempos no coinciden
A partir del dato de la intensidad del campo magnético, obtenemos el valor de P1/2 teniendo en cuenta que
- El campo magnético está en gauss (un gauss = 0.0001 T)
- Una unidad de masa atómica vale 1.67·10-27 kg.
- La carga del ión vale 1.6·10-19 C
Ejemplo
- Se elige como partícula el protón m=1.67·10-27 kg y carga q=1.6·10-19 C
- Campo magnético B=200 gauss=200·10-4 T
- Diferencia de potencial entre las D's, V=500 V
- El semiperiodo de la fem alterna 1.0 μs=1.0·10-6 s
- La partícula cargada parte del reposo v0=0, y se acelera por la diferencia de potencial V existente entre las dos D’s, ganado una energía qV.
-
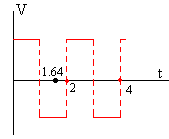
Como el periodo de la fem alterna es de 2·1.0=2.0 μs. Cuando la partícula completa su trayectoria semicircular encuentra que el campo existente entre las dos D’s acelera la partícula cargada, ganando una energía qV
-
En este instante, el campo existente entre las dos D’s se opone al movimiento de la partícula, perdiendo una energía qV. Como la energía de la partícula es qV, su velocidad es v3=v1, describe una semicircunferencia de radio r3=r1 empleando un tiempo de 1.64 μs en completarla.
-
En este instante, el campo existente entre las dos D’s se opone al movimiento de la partícula, perdiendo la energía qV que le quedaba, su velocidad final es v4=0
La partícula describe una trayectoria semicircular de radio r1
El tiempo t1 que tarda la partícula en recorrer la semicircunferencia es
Su velocidad v2 es
La partícula describe una trayectoria semicircular de radio r1
El tiempo que tarada en describir la semicircunferencia es
que como vemos es independiente del radio
Completa la segunda semicircunferencia en el instante 2·1.64=3.28 μs
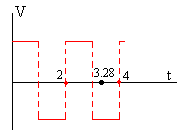
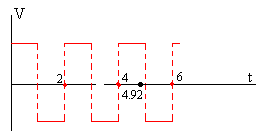
Completa la tercera semicircunferencia en el instante 3·1.64=4.92 μs
Manteniendo el tipo de partícula, protón, el campo magnético (200) y la diferencia de potencial entre las D's (500). Probar con
- El semiperiodo de la fem alterna 1.5 μs
Disminuir luego, la diferencia de potencial (200), comprobar que 1.5 μs no es un tiempo apropiado para acelerar esta partícula
Actividades
- Se selecciona el ión que se va a acelerar, en el control titulado Partícula .
Se introduce
- la intensidad del campo magnético (en gauss=10-4 T), en el control titulado Campo magnético
- la diferencia de potencial (en volts) entre las 'Ds', en el control titulado Diferencia de potencial
- el tiempo en microsegundos (1μs=10-6 s) que corresponde a un semiperiodo del potencial alterno, en el control titulado Semiperiodo
Se pulsa en el botón Nuevo.
A medida que transcurre el tiempo, vemos como cambia la polaridad de los terminales marcados con los signos + y - situados en la parte inferior del ciclotrón. Una flecha en la región ente las dos D's indica el sentido del campo eléctrico en la región entre las dos D's
Si no introducimos el tiempo adecuado, observamos que el campo eléctrico existente en la región comprendida entre las dos D's acelera primero los iones y luego, los frena hasta que eventualmente los para, en ese momento se deja de trazar la trayectoria.

