Efecto Hall
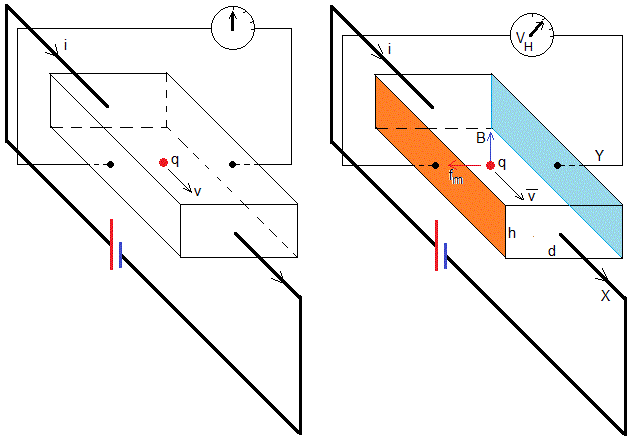
En la figura se muestra una lámina de un material que conduce una corriente de intensidad i cuando sus extremos se conectan a una batería. Si medimos la diferencia de potencial entre los lados opuestos, nos dará cero, tal como se muestra en la figura de la izquierda.
La situación cambia cuando se aplica un campo magnético B perpendicular a la corriente en la lámina, veremos que aparece una diferencia de potencial VH muy pequeña entre los lados opuestos tal como se muestra en la figura de la derecha.
Recordamos el concepto de intensidad de la corriente: i=nqv(hd)
- n es el número de portadores de carga por unidad de volumen
- q es la carga de cada portador, 1.6·10-19 C
- hd es el área la sección rectangular de la placa conductora
- v es la velocidad media de los portadores de carga
En ausencia de campo magnético los portadores de carga se mueven a lo largo del eje X con velocidad media v
La fuerza que ejerce el campo magnético sobre un portador de carga es
Debido a esta fuerza, los los portadores de carga adquieren una componente de la velocidad a lo largo del eje Y. Como no es posible que fluya una corriente en la dirección Y, los portadores crean un campo eléctrico E en la dirección Y que es suficiente para que la corriente en esta dirección sea nula
Esta es la situación de equilibrio o el estado estacionario, en el cual las fuerzas magnética fm=qvB y eléctrica fe=qE sobre los portadores de carga en la dirección Y se cancelan, fm=fe
La diferencia de potencial que se establece entre los lados opuestos es
La diferencia de potencial VH es proporcional a la intensidad i y al campo magnético B.
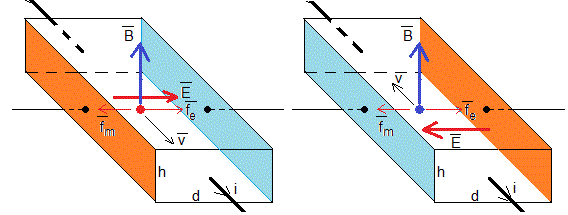
Si el portador de carga es negativo (electrones en un metal), figura de la derecha, la fuerza magnética es de sentido contrario al producto vectorial , el campo eléctrico cambia de sentido y el voltímetro medirá una diferencia de potencial de sentido contrario. El efecto Hall distingue el signo de los portadores de carga lo que se aplica en los semiconductores.
Número de electrones de valencia
En un conductor los electrones se mueven con diferentes velocidades y en todas las direcciones, la velocidad media es cero. Cuando se establece un campo eléctrico, conectándolo a una batería, los electrones se mueven con diferentes velocidades y en todas las direcciones pero en valor medio no nulo v, en la dirección del campo eléctrico.
Los electrones de valencia son los electrones que se encuentran en la capa de mayor nivel de energía del átomo, siendo estos los responsables de la interacción entre átomos de distintos elementos o entre los átomos del mismo elemento. En los conductores forman un gas de electrones que es el responsable de las propiedades eléctricas de estos materiales
Conocida la intensidad i=nqv(hd), calculamos la velocidad media v si conocemos el número de portadores de carga por unidad de volumen, n
Sea un conductor
- Densidad, ρ
- Masa atómica, A
- Número de electrones de valencia por cada átomo, z
En un volumen V de conductor hay N átomos. La densidad n de electrones que contribuyen a la conducción (número de electrones por unidad de volumen) es n=zN/V. Si M=ρV es la masa de conductor contenida en el volumen V de un material de densidad ρ, tendremos
Pero M/N es la masa de un átomo, que es igual a la masa atómica dividido por el número de Avogadro, A/NA
Ejemplo
Sea una lámina de cobre, supongamos que cada átomo de cobre tiene un electrón en su capa exterior (z=1) que contribuye a la corriente eléctrica.
- NA=6.0225·1023 mol-1, es el número de Avogadro
- A=63.54 g/mol, es la masa atómica del cobre
- ρ=8.89 g/cm3, es la densidad del cobre
El número de electrones que contribuyen a la conducción de la corriente eléctrica por unidad de volumen es, n=8.426·1022 cm-3
Conocida la intensidad i de la corriente en amperios, despejamos la velocidad v en cm/s
La lámina de cobre de ancho d=1.5 cm y espesor h=0.125 cm se coloca perpendicularmente a un campo magnético B=1.17 T. A lo largo de la lámina circula una corriente de intensidad i=100 A. Calculamos:
- La velocidad (media) de desplazamiento de los electrones
- La diferencia de potencial entre las caras opuestos de la lámina
v=0.0396 cm/s
VH=(0.0396/100)·1.17·(1.5/100)=6.94·10-6 V
El efecto Hall nos permite conocer el signo de los portadores de carga y el número de electrones de valencia z de los átomos de un determinado material conductor, midiendo la diferencia de potencial VH entre las caras opuestos de la lámina
Si conocemos z que para los metales alcalinos es la unidad, despejamos de la fórmula el número NAq denominado constante de Faraday, F. Esta constante se utiliza en las reacciones electroquímicas, para calcular la cantidad de sustancia que se deposita en un placa cuando pasa una corriente durante un tiempo
Radio de un ión
Todos los materiales cristalinos adoptan una distribución regular de átomos o iones en el espacio. Se define la celda unitaria como la porción más simple de una estructura cristalina que al repetirse mediante traslación reproduce todo el cristal. Consideraremos las más sencillas: la celda primitiva, la centrada en el cuerpo y la centrada en las caras
Celda primitiva
Se dibuja un cubo de lado a y se sitúa un átomo de radio r en cada vértice
R=1/2; %radio
hold on
%centros de los átomos
vertices=[[0,0,0],[1,0,0],[0,1,0],[0,0,1],[1,1,0],[1,0,1],[0,1,1],[1,1,1]];
for i=1:3:length(vertices)
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=vertices(i)+R*sin(phi).*cos(theta);
y=vertices(i+1)+R*sin(phi).*sin(theta);
z=vertices(i+2)+R*cos(phi);
h1=surfl(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.7,'FaceAlpha',0.7)
plot3(vertices(i), vertices(i+1), vertices(i+2),
'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
end
shading interp
colormap(gray);
%celda unidad
line([0,0],[0,0],[0,1],'lineWidth',1.5,'color','r')
line([0,1],[0,0],[0,0],'lineWidth',1.5,'color','r')
line([0,0],[0,1],[0,0],'lineWidth',1.5,'color','r')
line([0,0],[0,1],[1,1],'lineWidth',1.5,'color','r')
line([0,1],[0,0],[1,1],'lineWidth',1.5,'color','r')
line([1,1],[0,1],[0,0],'lineWidth',1.5,'color','r')
line([0,1],[1,1],[0,0],'lineWidth',1.5,'color','r')
line([1,1],[0,1],[1,1],'lineWidth',1.5,'color','r')
line([0,1],[1,1],[1,1],'lineWidth',1.5,'color','r')
line([1,1],[0,0],[0,1],'lineWidth',1.5,'color','r')
line([1,1],[1,1],[0,1],'lineWidth',1.5,'color','r')
line([0,0],[1,1],[0,1],'lineWidth',1.5,'color','r')
hold off
axis equal
view(20,10)
axis off
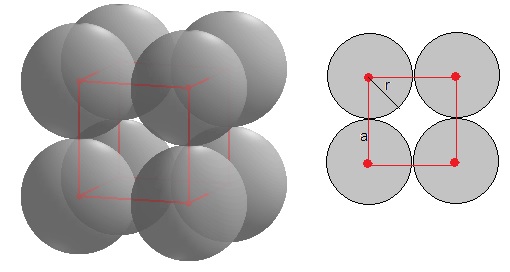
La relación es r=a/2. Como vemos, la celda de volumen a3 está ocupada por el volumen de un átomo, (ocho octavos de esfera), 4πr3/3
Se define factor de empaquetamiento fe al cociente entre el volumen de los átomos contenidos en la celda y el volumen de la celda, es la proporción de espacio de la celda ocupado por los átomos. fe es un factor geométrico
Centrada en las caras
Se dibuja un cubo de lado a, se sitúa un átomo de radio r en cada vértice y otro átomo en medio de cada una de las seis caras
R=sqrt(2)/4; %radio
hold on
%átomos
vertices=[[0,0,0],[1,0,0],[0,1,0],[0,0,1],[1,1,0],[1,0,1],[0,1,1],[1,1,1],
[0.5,0.5,0],[0,0.5,0.5],[0.5,0,0.5],[0.5,0.5,1],[1,0.5,0.5],[0.5,1,0.5]];
for i=1:3:length(vertices)
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=vertices(i)+R*sin(phi).*cos(theta);
y=vertices(i+1)+R*sin(phi).*sin(theta);
z=vertices(i+2)+R*cos(phi);
h1=surfl(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.7,'FaceAlpha',0.7)
plot3(vertices(i), vertices(i+1), vertices(i+2), 'o','markersize',
4,'markeredgecolor','r','markerfacecolor','r')
end
shading interp
colormap(gray);
%celda unidad
line([0,0],[0,0],[0,1],'lineWidth',1.5,'color','r')
line([0,1],[0,0],[0,0],'lineWidth',1.5,'color','r')
line([0,0],[0,1],[0,0],'lineWidth',1.5,'color','r')
line([0,0],[0,1],[1,1],'lineWidth',1.5,'color','r')
line([0,1],[0,0],[1,1],'lineWidth',1.5,'color','r')
line([1,1],[0,1],[0,0],'lineWidth',1.5,'color','r')
line([0,1],[1,1],[0,0],'lineWidth',1.5,'color','r')
line([1,1],[0,1],[1,1],'lineWidth',1.5,'color','r')
line([0,1],[1,1],[1,1],'lineWidth',1.5,'color','r')
line([1,1],[0,0],[0,1],'lineWidth',1.5,'color','r')
line([1,1],[1,1],[0,1],'lineWidth',1.5,'color','r')
line([0,0],[1,1],[0,1],'lineWidth',1.5,'color','r')
hold off
axis equal
view(20,10)
axis off
La relación es . Como vemos, la celda de volumen a3 está ocupada por el volumen de cuatro átomos, (ocho octavos de esfera más seis medias esferas), 4·4πr3/3
Centrada en el cuerpo
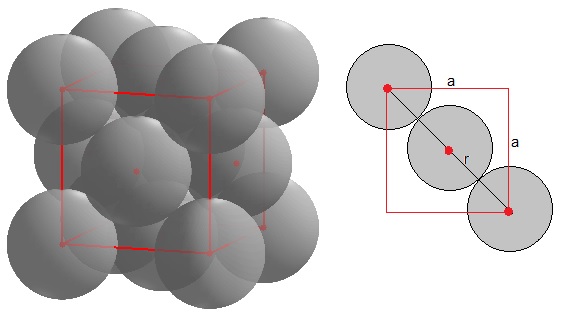
Se dibuja un cubo de lado a, se sitúa un átomo de radio r en cada vértice y otro en medio del cubo
R=sqrt(3)/4; %radio
hold on
%átomos
vertices=[[0,0,0],[1,0,0],[0,1,0],[0,0,1],[1,1,0],[1,0,1],
[0,1,1],[1,1,1],[0.5,0.5,0.5]];
for i=1:3:length(vertices)
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=vertices(i)+R*sin(phi).*cos(theta);
y=vertices(i+1)+R*sin(phi).*sin(theta);
z=vertices(i+2)+R*cos(phi);
h1=surfl(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.7,'FaceAlpha',0.7)
plot3(vertices(i), vertices(i+1), vertices(i+2), 'o','markersize',4,
'markeredgecolor','r','markerfacecolor','r')
end
shading interp
colormap(gray);
%celda unidad
line([0,0],[0,0],[0,1],'lineWidth',1.5,'color','r')
line([0,1],[0,0],[0,0],'lineWidth',1.5,'color','r')
line([0,0],[0,1],[0,0],'lineWidth',1.5,'color','r')
line([0,0],[0,1],[1,1],'lineWidth',1.5,'color','r')
line([0,1],[0,0],[1,1],'lineWidth',1.5,'color','r')
line([1,1],[0,1],[0,0],'lineWidth',1.5,'color','r')
line([0,1],[1,1],[0,0],'lineWidth',1.5,'color','r')
line([1,1],[0,1],[1,1],'lineWidth',1.5,'color','r')
line([0,1],[1,1],[1,1],'lineWidth',1.5,'color','r')
line([1,1],[0,0],[0,1],'lineWidth',1.5,'color','r')
line([1,1],[1,1],[0,1],'lineWidth',1.5,'color','r')
line([0,0],[1,1],[0,1],'lineWidth',1.5,'color','r')
hold off
axis equal
view(20,10)
axis off
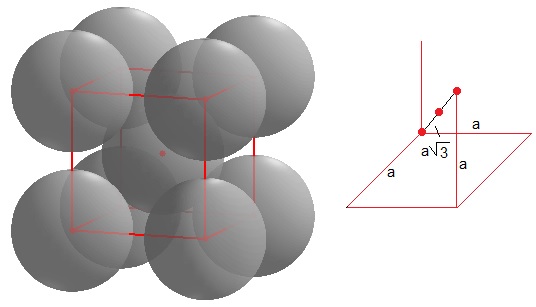
La relación es . Como vemos, la celda de volumen a3 está ocupada por el volumen de dos átomos, (ocho octavos de esfera más una esfera en el centro del cubo), 2·4πr3/3
La densidad a escala microscópica es el cociente entre la masa de los átomos contenidos en la celda unidad y el volumen de dicha celda, Vc
La masa ma de cada átomo es el cociente entre la masa atómica, A y el número de Avogadro NA. nc es el número de átomos en cada celda unidad que ya hemos calculado: 1, 4, 2
El factor de empaquetamiento, que ya hemos calculado para una celda cúbica, Vc=a3, es el cociente
Despejamos el radio del ión, r
En el apartado anterior, hemos deducido que la densidad n de electrones que contribuyen a la conducción (número de electrones por unidad de volumen) es
El radio r del ión está directamente relacionado con la densidad n de electrones de conducción
Para los metales alcalinos, que son monovalentes, z=1, adoptan una estructura cristalina, cúbica centrada en el cuerpo, , entonces
Recordaremos que la densidad de electrones n se puede medir a través del efecto Hall
Donde i es la intensidad de la corriente, B es el campo magnético aplicado perpendicular a la lámina de material de espesor h, q=1.6·10-19 C es la carga del electrón, VH es la diferencial de potencial entre los lados opuestos de la lámina (dirección Y) debido al efecto Hall
Los radios de los metales alcalinos se pueden determinar de forma experimental por medio del efecto Hall
Soluciones de sal en agua
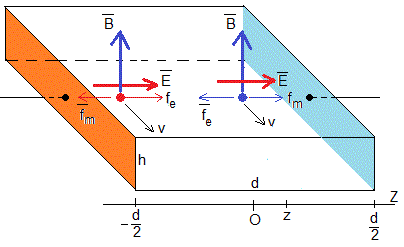
Supongamos una solución de agua salada que fluye a través de una tubería de sección rectangular tal como se aprecia en la figura. Dos lados opuestos de la tubería son láminas metálicas de altura h.
Sea v la velocidad media del fluido o de los iones sodio (positivos) y cloro (negativos). Como vemos en la figura, la fuerza que ejerce el campo magnético fm=qvB desvía a los iones positivos hacia la izquierda y los iones negativos hacia la derecha. Se establece un campo eléctrico E de izquierda a derecha que se opone a la acumulación de carga fe=qE. Los iones no se desvían cuando E=vB y diferencia de potencial entre las dos placas metálicas es V'-V=vBd
Por ejemplo, si fluye agua a razón de Q=1 litro/s y h=0.05 m. y B=1.0 T
V'-V=QBd/(hd)=QB/h=10-3·1/0.05=20 mV
Distribución de carga
Cuando estudiamos la viscosidad de un fluido que circula en régimen laminar por una tubería, obtuvimos un perfil de velocidades en función de la distancia radial, al eje del tubo.
Supongamos que la velocidad del fluido varía a lo largo del eje Z, de modo que es cero en las caras metálicas opuestas (z=-d/2 y z=d/2) y máximo en el centro z=0. La velocidad media v y el gasto Q se calculan del siguiente modo
Como la velocidad del fluido varía con z, el campo eléctrico no es constante E=v(z)B, es nulo en las caras metálicas opuestas (z=-d/2 y z=d/2). La consecuencia es que la densidad de carga λ(z) no es constante.
La diferencia de potencial V'-V es proporcional al campo magnético B y a la velocidad media v del fluido o al gasto Q
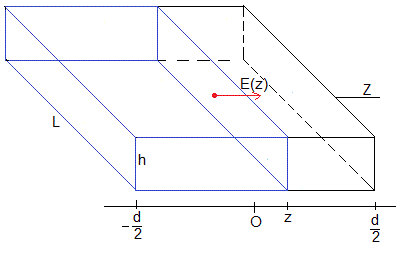
Aplicamos la ley de Gauss, tomando una superficie cerrada en forma de prisma de longitud L, altura h y anchura d/2+z, en color azul en la figura. El campo eléctrico es paralelo al eje Z, de modo que solamente hay flujo a través de una cara
E(z)·(hL)
La carga en el interior de la superficie cerrada es
siendo λ(z)=ρ(z)·hL la carga por unidad de longitud a lo largo del eje Z y ρ(z) la carga por unidad de volumen. Sea ε la permitividad del fluido, la ley de Gauss se escribe
Obtenemos v(z) a partir de λ(z) integrando u obtenemos λ(z) en términos de v(z) diferenciando
La densidad de carga es la suma de la densidad de carga de los iones positivos y de la densidad de carga de los iones negativos
Perfiles de velocidad
Supongamos el siguiente perfil v(z), la velocidad del fluido es nula en las caras opuestas (z=-d/2 y z=d/2) y es máxima v0 en el centro z=0
Calculamos la velocidad media v
El resultado de la integral nos dice que a velocidad media del fluido es dos tercios de la velocidad máxima en el centro v0.
Para este perfil de velocidades la densidad de carga es
v=@(x) 1-4*x^2;
l=@(x) -x;
subplot(2,1,1)
fplot(v,[-0.5,0.5])
grid on
xlabel('z/d')
ylabel('v(z)')
title('Perfil de velocidades')
subplot(2,1,2)
fplot(l,[-0.5,0.5])
grid on
xlabel('z/d')
ylabel('\lambda(z)')
title('Densidad de carga')
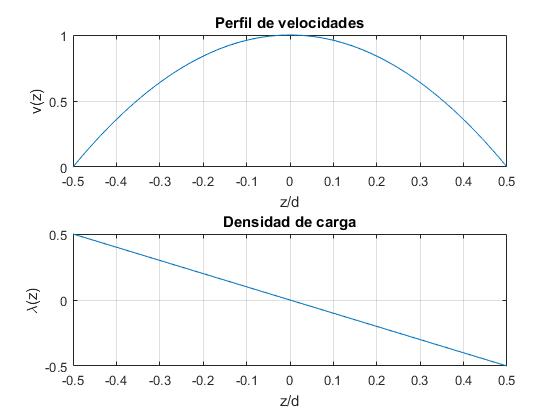
La densidad de carga varía linealmente con z, es positiva entre z=-d/2 y z=0 y es negativa desde z=0 a z=d/2.
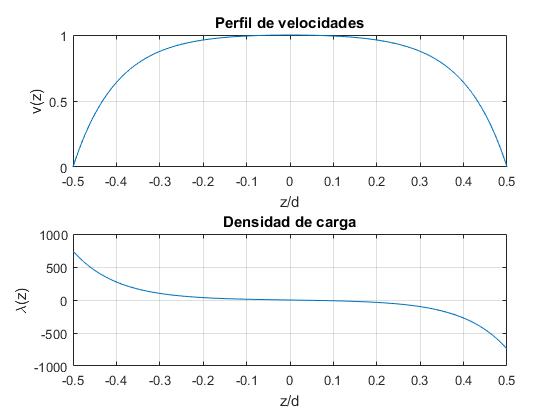
Consideremos ahora otra función v(z), que podría describir mejor el perfil de velocidades de los fluidos reales, de modo que la velocidad del fluido es máxima y casi constante en el interior de la tubería y disminuye rápidamente a cero en las proximiades de las paredes. Está dado por la siguiente fórmula, en la que k es un parámetro ajustable
La densidad de carga es
k=10;
v=@(x) (cosh(k/2)-cosh(k*x))/(cosh(k/2)-1);
l=@(x) -k*sinh(k*x);
subplot(2,1,1)
fplot(v,[-0.5,0.5])
grid on
xlabel('z/d')
ylabel('v(z)')
title('Perfil de velocidades')
subplot(2,1,2)
fplot(l,[-0.5,0.5])
grid on
xlabel('z/d')
ylabel('\lambda(z)')
title('Densidad de carga')
Referencias
Ahmed Houari. Useful pedagogical applications of the classical Hall effect. Physics Education, 42 (6) 2007, pp. 603-606
Ahmed Houari. Hall determination of atomic radii of alkali metals. Physics Education, 43 (5) 2008, pp. 519-521
R De Luca. Lorentz force on sodium and chlorine ions in a salt water solution flow under a transverse magnetic field. Eur. J. Phys. 30 (2009) 459-466

