Movimiento de un dipolo eléctrico en un campo magnético uniforme

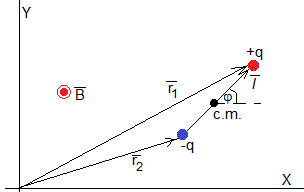
Consideremos un dipolo eléctrico, formado por dos partículas de la misma masa m con cargas +q y -q unidas por una varilla rígida de longitud l y de masa despreciable, que se mueve en el plano XY bajo la acción de un campo magnético a lo largo del eje Z, tal como se muestra en la figura.

La posición del centro de masas es

$\vec{r_{c m}} = \frac{1}{2} (\vec{r_{1}} + \vec{r_{2}})$

La velocidad del centro de masas

$\vec{v_{c m}} = \frac{1}{2} (\vec{v_{1}} + \vec{v_{2}})$

La posición relativa de las partículas

$\vec{l} = \vec{r_{1}} - \vec{r_{2}}$

La velocidad relativa

$\frac{d \vec{l}}{d t} = \vec{v_{1}} - \vec{v_{2}}$

$\vec{l}$ es un vector de longitud fija

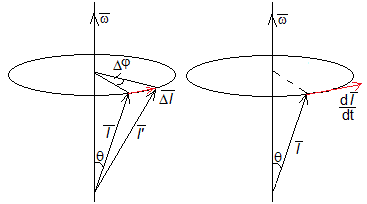
Representamos dicho vector en el instante t y en el instante t+Δt

El cambio $\vec{Δ l} = \vec{l'} - \vec{l}$ , es un vector dibujado en color rojo, cuya longitud es aproximadamente el arco de la circunferencia lsinθ·Δφ. La razon del cambio con el tiempo es

$\frac{Δ l}{Δ t} \approx \frac{Δ φ}{Δ t} l \sin θ$

En el límite cuando Δt→0

$\frac{d l}{d t} = ω l \sin θ$

cuya dirección es tangente a la circunferencia. En forma vectorial

$\frac{d \vec{l}}{d t} = \vec{ω} \times \vec{l}, \vec{ω} = ω \hat{k} = \frac{d φ}{d t} \hat{k}$

Ecuaciones del movimiento y magnitudes que se conservan (I)

Tenemos dos ecuaciones del movimiento: traslación del centro de masas y movimiento de rotación alrededor de un eje perpendicular al plano XY y que pasa por el centro de masas del dipolo

Traslación del c.m.

Calculamos la fuerza que ejerce el campo magnético sobre cada una de las dos cargas del dipolo

$\begin{array}{l} \vec{F} = {\vec{F}}_{1} + \vec{F_{2}} = q (\vec{v_{1}} \times \vec{B}) + (- q) (\vec{v_{2}} \times \vec{B}) = q (\vec{v_{1}} - \vec{v_{2}}) \times \vec{B} \\ \vec{F} = q \frac{d \vec{l}}{d t} \times \vec{B} \end{array}$

La ecuación del movimiento del centro de masas es

$\begin{array}{l} 2 m \frac{d \vec{v_{c m}}}{d t} = q \frac{d \vec{l}}{d t} \times \vec{B} \\ \frac{d}{d t} {2 m \vec{v_{c m}} - q (\vec{l} \times \vec{B})} = 0 \end{array}$

La carga q es constante y el vector campo magnético es constante

Tenemos una magnitud, momento lineal, $\vec{p}$ , que se mantiene constante

$\vec{p} = 2 m \vec{v_{c m}} - q \vec{l} \times \vec{B}$

Movimiento de rotación alrededor de un eje que pasa por el c.m.

Calculamos el momento de las fuerzas que actúan sobre cada una de las dos partículas respecto del centro de masas

$\begin{array}{l} \vec{M} = (\frac{\vec{l}}{2}) \times {\vec{F}}_{1} + (- \frac{\vec{l}}{2}) \times \vec{F_{2}} = q \frac{\vec{l}}{2} \times (\vec{v_{1}} \times \vec{B}) + q \frac{\vec{l}}{2} \times (\vec{v_{2}} \times \vec{B}) = q \vec{l} \times (\frac{\vec{v_{1}} + \vec{v_{2}}}{2} \times \vec{B}) \\ \vec{M} = q \vec{l} \times (\vec{v_{c m}} \times \vec{B}) \end{array}$

El momento angular del dipolo respecto del centro de masas

$\vec{L} = I \vec{ω} = (m {(\frac{l}{2})}^{2} + m {(\frac{l}{2})}^{2}) = \frac{1}{2} m l^{2} \vec{ω}$

La ecuación del movimiento de rotación alrededor de un eje perpenducular que pasa por el c.m. es

$I \frac{d \vec{ω}}{d t} = q \vec{l} \times (\vec{v_{c m}} \times \vec{B}), I = \frac{1}{2} m l^{2}$

Conservación de la magnitud J

Existe otra constante del movimiento que se obtiene, evaluando la expresión

$\frac{d}{d t} (I \vec{ω} \cdot \vec{B}) = \vec{B} (I \frac{d \vec{ω}}{d t}) = q \vec{B} \cdot (\vec{l} \times (\vec{v_{c m}} \times \vec{B}))$

Teniendo en cuenta la propiedad

$\vec{A_{1}} \cdot (\vec{A_{2}} \times \vec{A_{3}}) = (\vec{A_{1}} \times \vec{A_{2}}) \cdot \vec{A_{3}}$

El resultado es

$\begin{array}{l} q \vec{B} \cdot (\vec{l} \times (\vec{v_{c m}} \times \vec{B})) = q (\vec{B} \times \vec{l}) \cdot (\vec{v_{c m}} \times \vec{B}) = (\vec{p} - 2 m \vec{v_{c m}}) \cdot (\vec{v_{c m}} \times \vec{B}) \\ = \vec{p} \cdot (\vec{v_{c m}} \times \vec{B}) = (\vec{p} \times \vec{v_{c m}}) \cdot \vec{B} = - (\vec{v_{c m}} \times \vec{p}) \cdot \vec{B} \\ \frac{d}{d t} (I \vec{ω} \cdot \vec{B}) = - \frac{d}{d t} {(\vec{r_{c m}} \times \vec{p}) \cdot \vec{B}} \\ \frac{d}{d t} {I \vec{ω} \cdot \vec{B} + (\vec{r_{c m}} \times \vec{p}) \cdot \vec{B}} = 0 \end{array}$

Denominamos J a la nueva constante del movimiento

$J = I \vec{ω} \cdot \vec{B} + (\vec{r_{c m}} \times \vec{p}) \cdot \vec{B}$

Conservación de la energía

La fuerza que ejerce el campo magnético sobre una partícula cargada es perpendicular al desplazamiento. No realiza trabajo alguno, la energía permanece constante. Lo comprobamos evaluando la expresión

$\begin{array}{l} \frac{d}{d t} (\frac{1}{2} 2 m v_{c m}^{2} + \frac{1}{2} I ω^{2}) = \frac{1}{2} \frac{d}{d t} (2 m \vec{v_{c m}} \cdot \vec{v_{c m}} + I \vec{ω} \cdot \vec{ω}) = \vec{v_{c m}} \cdot 2 m \frac{d \vec{v_{c m}}}{d t} + \vec{ω} \cdot I \frac{d \vec{ω}}{d t} \\ = \vec{v_{c m}} \cdot q (\vec{ω} \times \vec{l}) \times \vec{B} + \vec{ω \cdot} q \vec{l} \times (\vec{v_{c m}} \times \vec{B}) = q {(\vec{v_{c m}} \times (\vec{ω} \times \vec{l})) \cdot \vec{B} + (\vec{ω} \times \vec{l}) \cdot (\vec{v_{c m}} \times \vec{B})} = \\ q {(\vec{v_{c m}} \times (\vec{ω} \times \vec{l})) \cdot \vec{B} + (\vec{ω} \times \vec{l}) \cdot (\vec{v_{c m}} \times \vec{B})} = q {(\vec{v_{c m}} \times (\vec{ω} \times \vec{l})) \cdot \vec{B} + ((\vec{ω} \times \vec{l}) \times \vec{v_{c m}}) \cdot \vec{B}} = \\ q {(\vec{v_{c m}} \times (\vec{ω} \times \vec{l})) \cdot \vec{B} - (\vec{v_{c m}} \times (\vec{ω} \times \vec{l})) \cdot \vec{B}} = 0 \end{array}$

La energía E permanece constante

$E = m (v_{x}^{2} + v_{y}^{2}) + \frac{1}{2} I ω^{2}$

Ecuaciones del movimiento y magnitudes que se conservan (II)

En este apartado, vamos a escribir las ecuaciones del movimiento y las magnitudes que se conservan de forma apropiada para el cálculo y la representación gráfica.

Movimiento de traslación del centro de masas

$\begin{array}{l} \vec{p} = 2 m \vec{v_{c m}} - q \vec{l} \times \vec{B} \\ \vec{p} = 2 m (v_{x} \hat{i} + v_{y} \hat{j}) - q (l \cos φ \hat{i} + l \sin φ \hat{j}) \times B \hat{k} \\ {\begin{cases} p_{x} = 2 m v_{x} - q l B \sin φ \\ p_{y} = 2 m v_{y} + q l B \cos φ \end{cases} \end{array}$

Donde p_x y p_y son constantes que se determinan a partir de las condiciones iniciales.

El centro de masas del dipolo parte del origen en reposo, orientado a lo largo del eje X, se le imparte una velocidad angular inicial ω₀. En el instante t=0, x=0, y=0, v_x=0, v_y=0, φ=0, ω=dφ/dt=ω₀. Por tanto, p_x=0 y p_y=qlB

$\begin{array}{l} {\begin{cases} v_{x} = \frac{l}{2} ω_{c} \sin φ \\ v_{y} = \frac{l}{2} ω_{c} (1 - \cos φ) \end{cases} \\ \frac{d^{2} φ}{d t^{2}} = - ω_{c}^{2} \sin φ \end{array}$

Movimiento de rotación

$\begin{array}{l} I \frac{d \vec{ω}}{d t} = q \vec{l} \times (\vec{v_{c m}} \times \vec{B}), I = \frac{1}{2} m l^{2} \\ \frac{1}{2} m l^{2} \frac{d^{2} φ}{d t^{2}} \hat{k} = q (l \cos φ \hat{i} + l \sin φ \hat{j}) \times ((v_{x} \hat{i} + v_{y} \hat{j}) \times B \hat{k}) \\ \frac{1}{2} m l^{2} \frac{d^{2} φ}{d t^{2}} \hat{k} = q (l \cos φ \hat{i} + l \sin φ \hat{j}) \times (v_{y} B \hat{i} - v_{x} B \hat{j}) \\ \frac{d^{2} φ}{d t^{2}} = - \frac{2 q B}{m l} (v_{x} \cos φ + v_{y} \sin φ) \\ \frac{d^{2} φ}{d t^{2}} = - \frac{2 q B}{m l} (\frac{q l B}{2 m} \sin φ \cos φ + \frac{q l B}{2 m} (1 - \cos φ) \sin φ) \\ \frac{d^{2} φ}{d t^{2}} = - \frac{q^{2} B^{2}}{m^{2}} \sin φ \\ \frac{d^{2} φ}{d t^{2}} = - ω_{c}^{2} \sin φ, ω_{c} = \frac{q B}{m} \end{array}$

La frecuencia angular ω_c aparece en la página titulada Movimiento de una partícula cargada en un campo eléctrico y en un campo magnético

La ecuación del movimiento de rotación es similar a la del péndulo simple

Conservación de la energía

$\begin{array}{l} \frac{1}{2} 2 m v_{c m}^{2} + \frac{1}{2} I ω^{2} = \frac{1}{2} I ω_{0}^{2} \\ 2 m (v_{x}^{2} + v_{y}^{2}) + (\frac{1}{2} m l^{2}) {(\frac{d φ}{d t})}^{2} = (\frac{1}{2} m l^{2}) ω_{0}^{2} \\ 4 \frac{q^{2} B^{2}}{m^{2}} \sin^{2} (\frac{φ}{2}) + {(\frac{d φ}{d t})}^{2} = ω_{0}^{2} \\ 4 ω_{c}^{2} \sin^{2} (\frac{φ}{2}) + {(\frac{d φ}{d t})}^{2} = ω_{0}^{2} \end{array}$

Conservación de la magnitud J

$\begin{array}{l} J = I \vec{ω} \cdot \vec{B} + (\vec{r_{c m}} \times \vec{p}) \cdot \vec{B} \\ J = \frac{1}{2} m l^{2} (ω \hat{k} \cdot B \hat{k}) + ((x \hat{i} + y \hat{j}) \times (p_{x} \hat{i} + p_{y} \hat{j})) \cdot B \hat{k} \\ J = \frac{1}{2} m l^{2} ω B + (x p_{y} - y p_{x}) B = \frac{1}{2} m l^{2} B (\frac{d φ}{d t}) + q B^{2} l x \end{array}$

Con las condiciones iniciales especificadas al principio de este apartado. En el instante inicial, t=0, x=0, φ=0, dφ/dt=ω₀

$J = \frac{1}{2} m l^{2} B ω_{0}$

La conservación de J se escribe

$ω_{0} = \frac{d φ}{d t} + 2 ω_{c} \frac{x}{l}$

Casos particulares

Resumimos las ecuaciones del movimiento

$\begin{array}{l} {\begin{cases} \frac{1}{l} \frac{d x}{d t} = \frac{1}{2} ω_{c} \sin φ \\ \frac{1}{l} \frac{d y}{d t} = ω_{c} \sin^{2} (\frac{φ}{2}) \end{cases} \\ \frac{d^{2} φ}{d t^{2}} = - ω_{c}^{2} \sin φ \end{array}$

junto con las magnitudes que se conservan

$\begin{array}{l} 4 ω_{c}^{2} \sin^{2} (\frac{φ}{2}) + {(\frac{d φ}{d t})}^{2} = ω_{0}^{2} \\ \frac{d φ}{d t} + 2 ω_{c} \frac{x}{l} = ω_{0} \end{array}$

Cuando la amplitud de las oscilaciones, en el movimiento de rotación, es pequeña

Hacemos la aproximación sinφ≈φ

La solución de la ecuación diferencial es la de un Movimiento Armónico Simple

$\begin{array}{l} φ = A \sin (ω_{c} t + δ) \\ \frac{d φ}{d t} = A ω_{c} \cos (ω_{c} t + δ) \end{array}$

La amplitud A y la fase inicial δ se determinan a partir de la condiciones iniciales, t=0, φ=0, dφ/dt=ω₀

$φ = \frac{ω_{0}}{ω_{c}} \sin (ω_{c} t)$

A partir, de la conservación de la energía, obtenemos la ordenada y/l del centro de masas

$\begin{array}{l} \sin^{2} (\frac{φ}{2}) = \frac{ω_{0}^{2}}{4 ω_{c}^{2}} \sin^{2} (ω_{c} t) \\ \frac{1}{l} \frac{d y}{d t} = \frac{ω_{0}^{2}}{4 ω_{c}} \sin^{2} (ω_{c} t) \\ \frac{y}{l} = \frac{ω_{0}^{2}}{8 ω_{c}} (t - \frac{1}{2 ω_{c}} \sin (2 ω_{c} t)) \end{array}$

A partir de la conservación de de la magnitud J, obtenemos la abscisa x/l del centro de masas

$\begin{array}{l} ω_{0} = ω_{0} \cos (ω_{c} t) + 2 ω_{c} \frac{x}{l} \\ \frac{x}{l} = \frac{ω_{0}}{ω_{c}} \sin^{2} (\frac{ω_{c} t}{2}) \end{array}$

Fijamos ω_c=1, y hacemos que la velocidad angular inicial de rotación sea ω₀=0.1, pequeña para asegurar que las oscilaciones angulares φ son aproximadamente armónicas

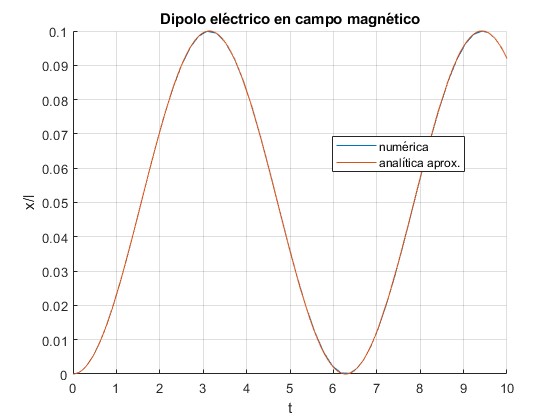
Resolvemos el sistema de tres ecuaciones diferenciales utilizando el procedimiento ode45 de MATLAB, hasta el instante t=10. Comprobamos que la solución numérica casi coincide con la analítica aproximada

Representamos la posición angular φ del dipolo en función del tiempo

w0=0.1;
wc=1;
f=@(t,x) [wc*sin(x(3))/2; wc*sin(x(3)/2)^2; x(4); -wc^2*sin(x(3))];
[t,x]=ode45(f,[0,10],[0,0,0,w0]);
hold on
plot(t,x(:,3))
fplot(@(t) w0*sin(wc*t)/wc,[0,10])
hold off
grid on
legend('numérica','analítica aprox.','location','best')
xlabel('t')
ylabel('\phi')
legend('numérica','analítica aprox.','location','best')
title('Dipolo eléctrico en campo magnético')

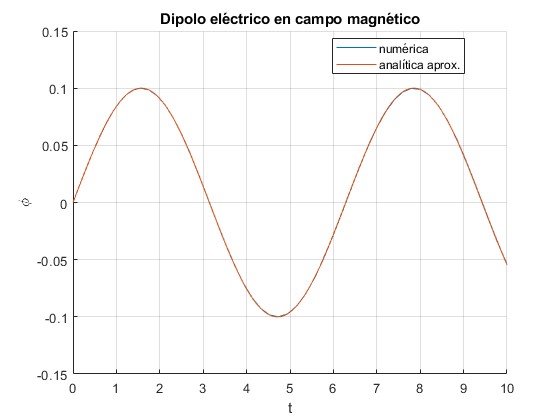
Representamos la abscisa x/l del centro de masa del dipolo en función del tiempo

w0=0.1;
wc=1;
f=@(t,x) [wc*sin(x(3))/2; wc*sin(x(3)/2)^2; x(4); -wc^2*sin(x(3))];
[t,x]=ode45(f,[0,10],[0,0,0,w0]);
hold on
plot(t,x(:,1))
fplot(@(t) w0*sin(wc*t/2).^2/wc,[0,10])
hold off
grid on
legend('numérica','analítica aprox.','location','best')
xlabel('t')
ylabel('x/l')
title('Dipolo eléctrico en campo magnético')

Representamos la ordenada y/l del centro de masa del dipolo en función del tiempo

w0=0.1;
wc=1;
f=@(t,x) [wc*sin(x(3))/2; wc*sin(x(3)/2)^2; x(4); -wc^2*sin(x(3))];
[t,x]=ode45(f,[0,10],[0,0,0,w0]);
hold on
plot(t,x(:,2))
fplot(@(t) w0^2*(t-sin(2*wc*t)/(2*wc))/(8*wc),[0,10])
hold off
grid on
legend('numérica','analítica aprox.','location','best')
xlabel('t')
ylabel('y/l')
title('Dipolo eléctrico en campo magnético')

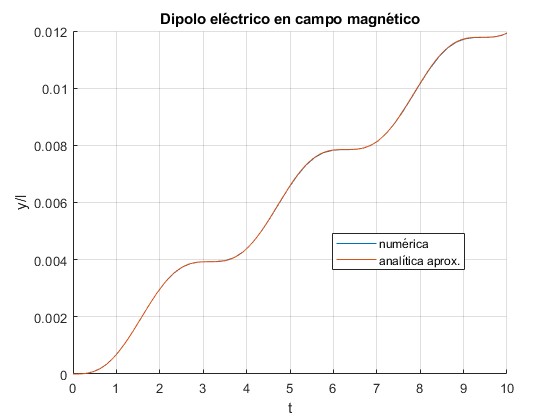
Oscilaciones y rotaciones

Utilizando la conservación de la energía, vemos que el mínimo valor de la velocidad angular dφ/dt se obtiene para φ=π, lo mismo que en un péndulo simple

$\begin{array}{l} 4 ω_{c}^{2} \sin^{2} (\frac{φ}{2}) + {(\frac{d φ}{d t})}^{2} = ω_{0}^{2} \\ 4 ω_{c}^{2} + {(\frac{d φ}{d t})}^{2} = ω_{0}^{2} \\ {(\frac{d φ}{d t})}^{2} = ω_{0}^{2} - 4 ω_{c}^{2} \end{array}$

Si ω₀<2ω_c, el dipolo no alcanza la posición angular φ=π, tenemos oscilaciones. Fijamos ω_c=1, y probamos con ω₀=1.8

Representamos la trayectoria del centro de masas hasta el instante t=10

w0=1.8;
wc=1;
f=@(t,x) [wc*sin(x(3))/2; wc*sin(x(3)/2)^2; x(4); -wc^2*sin(x(3))];
[t,x]=ode45(f,[0,10],[0,0,0,w0]);
plot(x(:,1),x(:,2))
grid on
xlabel('x/l')
ylabel('y/l')
title('Dipolo eléctrico en campo magnético')
%conservación
E=x(:,4).^2+4*wc^2*sin(x(:,3)/2).^2;
J=x(:,4)+2*wc*x(:,1);

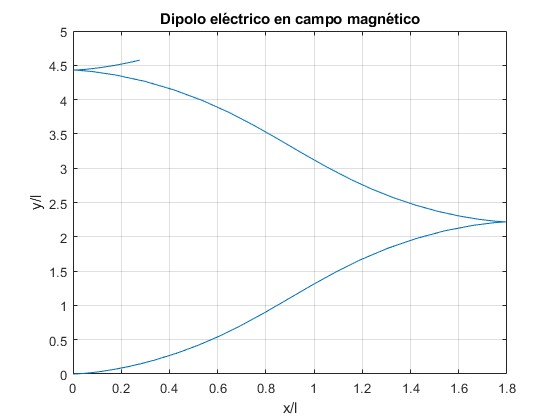
Representamos la posición angular φ en función del tiempo, modificando las líneas de código

...
plot(t,x(:,3))
xlabel('t')
ylabel('\phi')
...

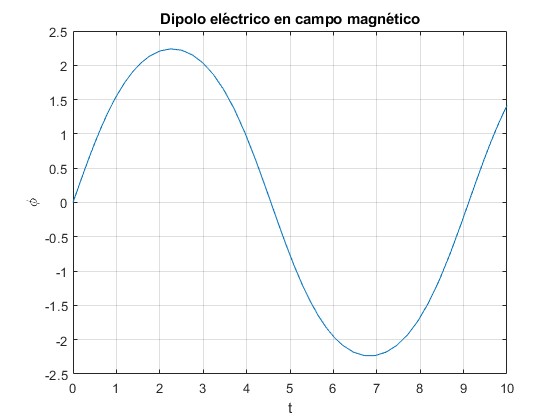
Comprobamos que la energía E y la magnitud J se mantienen constantes e iguales a sus valores iniciales $ω_{0}^{2}$ y ω₀, respectivamente

>> E
E 
    3.2400
    3.2400
    .....
    3.2369
    3.2369
>> J
J =
    1.8000
    1.8000
    .....
    1.8000
    1.8000

Si ω₀>2ω_c, el dipolo sobrepasa la posición angular φ=π, tenemos rotaciones. Fijamos ω_c=1, y probamos con ω₀=2.2

Representamos la trayectoria del centro de masas hasta el instante t=10

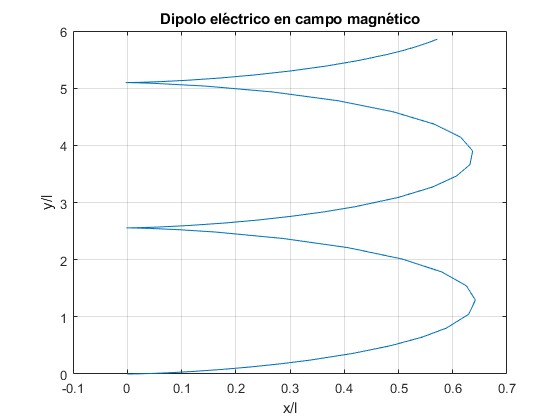
Representamos la posición angular φ en función del tiempo

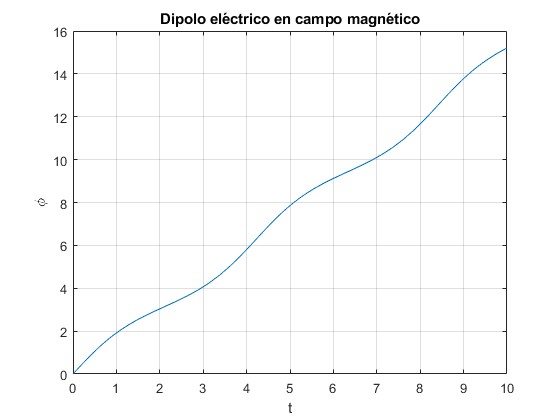
Comprobamos que la energía E y la magnitud J se mantienen constantes e iguales a sus valores iniciales $ω_{0}^{2}$ y ω₀, respectivamente

>> E
E 
    4.8400
    4.8400
   .....
    4.8719
    4.8719
>> J
J =
    2.2000
    2.2000
    .....
    2.2000
    2.2000

El caso más interesante se produce en la situación crítica, ω₀=2ω_c

La conservación de la energía establece

$\begin{array}{l} 4 ω_{c}^{2} \sin^{2} (\frac{φ}{2}) + {(\frac{d φ}{d t})}^{2} = 4 ω_{c}^{2} \\ \frac{d φ}{d t} = 2 ω_{c} \cos (\frac{φ}{2}) \\ \int_{0}^{φ} \frac{d φ}{\cos (\frac{φ}{2})} = 2 ω_{c} \int_{0}^{t} d t \end{array}$

Buscamos la integral en la tabla de integrales o bien, la obtenemos con Math Symbolic de MATLAB

>> syms x;
>> int(1/cos(x),x)
ans =log(1/cos(x)) + log(sin(x) + 1)

$\frac{1}{2} \ln | \frac{1 + \sin (\frac{φ}{2})}{\cos (\frac{φ}{2})} | = 2 ω_{c} t$

Se trata de una función implícita en φ, cuando t→∞ entonces φ→π y dφ/dt→0

La conservación de la magnitud J establece, la abscisa x/l del centro de masas

$\begin{array}{l} ω_{0} = \frac{d φ}{d t} + 2 ω_{c} \frac{x}{l} \\ 2 ω_{c} \approx 2 ω_{c} \frac{x}{l} \\ \frac{x}{l} \approx 1 \end{array}$

De la ecuación del movimiento, vemos que la ordenada y/l crece linealmente con el tiempo

$\begin{array}{l} \frac{1}{l} \frac{d y}{d t} = ω_{c} \sin^{2} (\frac{φ}{2}) \\ \frac{1}{l} \frac{d y}{d t} ≃ ω_{c} \\ \frac{y}{l} = ω_{c} t \end{array}$

Fijamos ω_c=1, y probamos con ω₀=2, hasta el tiempo t=5

Representamos la posición angular φ en función del tiempo t, observamos que tiende hacia π

w0=2;
wc=1;
f=@(t,x) [wc*sin(x(3))/2; wc*sin(x(3)/2)^2; x(4); -wc^2*sin(x(3))];
[t,x]=ode45(f,[0,5],[0,0,0,w0]);
plot(t,x(:,3))
grid on
xlabel('t')
ylabel('\phi')
title('Dipolo eléctrico en campo magnético')

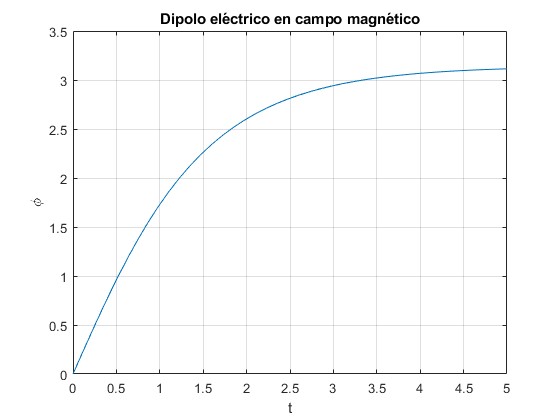
Modificamos las líneas de código, para representar la abscisa x/l del centro de masas en función del tiempo t, observamos que tiende hacia x/l=1

...
plot(t,x(:,1))
xlabel('t')
ylabel('x/l') 
...

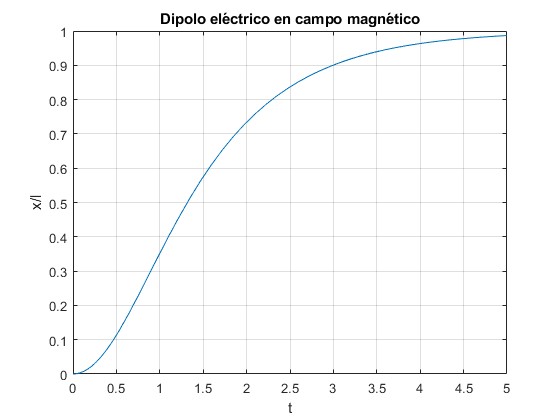
Modificamos las líneas de código, para representar la ordenada y/l del centro de masas en función del tiempo t, observamos que crece linealmente con el tiempo

...
plot(t,x(:,2))
xlabel('t')
ylabel('y/l') 
...

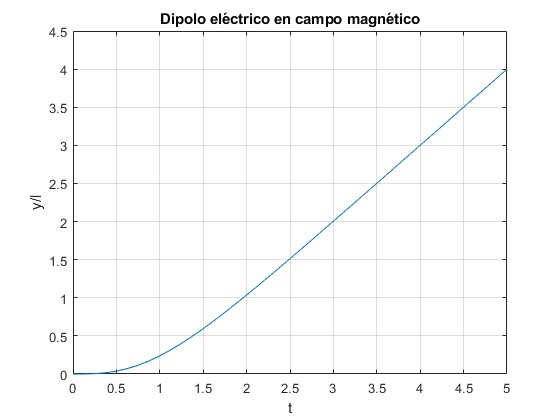
Actividades

Se introduce

Se fija que el centro de masas del dipolo parta del origen en reposo, orientado a lo largo del eje X. En el instante t=0, x=0, y=0, v_x=0, v_y=0, φ=0,
Se puede cambiar la velocidad inicial de rotación ω₀ del dipolo, en el control titulado Velocidad angular, dφ/dt=ω₀
Se ha fijado también, el valor del la frecuencia angular, ω_c=1

Se pulsa el botón titulado Nuevo

Se observa la trayectoria del centro de masas del dipolo y la rotación del mismo alrededor de un eje perpendicular que pasa por el c.m.

En la parte derecha, se proporcionan los datos de

El tiempo t
La posición (x/l, y/l) del centro de masas
La posición angular φ del dipolo
La velocidad angular ω=dφ/dt del dipolo

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

$| \frac{E - E_{0}}{E_{0}} | \cdot 100$

donde E es la energía del sistema en cualquier instante t y $E_{0} = ω_{0}^{2}$ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo en la parte inferior derecha. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

El mismo criterio se emplea para calcular el error relativo de la magnitud J

Velocidad angular ω₀:

Referencias

Asian Physics. (1st – 8th). Olympiad. Problems and Solutions. Editor Zheng Yongling. World Scientific (2010), pp. 36-43