Coordenadas cilíndricas

Las coordenadas cilíndricas, tienen por origen O y vectores unitaros, $\widehat{\rho }$, $\widehat{\phi }$ y $\widehat{k}$

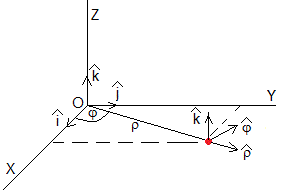
• Vector posición

${\displaystyle \overrightarrow{r}=\rho \widehat{\rho }+z\widehat{k}}$

• Vector velocidad

${\displaystyle \overrightarrow{v}=\frac{d\rho }{dt}\widehat{\rho }+\rho \frac{d\phi }{dt}\widehat{\phi }+\frac{dz}{dt}\widehat{k}}$

• Vector aceleración

${\displaystyle \frac{d^2\overrightarrow{r}}{d{t}^2}=\left(\frac{d^2\rho }{d{t}^2}-\rho {\left(\frac{d\phi }{dt}\right)}^2\right)\widehat{\rho }+\left(\rho \frac{d^2\phi }{d{t}^2}+2\frac{d\rho }{dt}\frac{d\phi }{dt}\right)\widehat{\phi }+\frac{d^{2}z}{d{t}^2}\widehat{k}}$

Momento angular

${\displaystyle \overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}=m\left|\begin{array}{ccc}\widehat{\rho }& \widehat{\phi }& \widehat{k}\\ \rho & 0& z\\ \frac{d\rho }{dt}& \rho \frac{d\phi }{dt}& \frac{dz}{dt}\end{array}\right|=-\rho z\frac{d\phi }{dt}\widehat{\rho }+\left(z\frac{d\rho }{dt}-\rho \frac{dz}{dt}\right)\widehat{\phi }+{\rho }^2\frac{d\phi }{dt}\widehat{k}}$

Movimiento de una partícula cargada en el campo magnético producido por una corriente rectilínea indefinida.

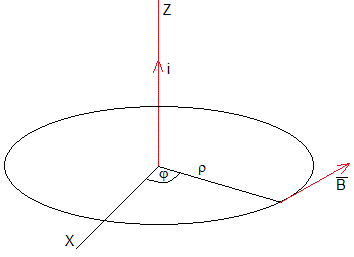
La corriente rectilínea indefinida tiene la dirección del eje Z. El campo magnético producido por esta corriente es perpendicular a la dirección radial y su sentido viene determinado por la regla de la mano derecha.

${\displaystyle \overrightarrow{B}=\frac{{\mu }_{0}i}{2\pi \rho }\widehat{\phi }}$

La fuerza que ejerce el campo magnético sobre una partícula cargada es

${\displaystyle \overrightarrow{F}=q\left(\overrightarrow{v}\times \overrightarrow{B}\right)=q\left|\begin{array}{ccc}\widehat{\rho }& \widehat{\phi }& \widehat{k}\\ \frac{d\rho }{dt}& \rho \frac{d\phi }{dt}& \frac{dz}{dt}\\ 0& \frac{{\mu }_{0}i}{2\pi \rho }& 0\end{array}\right|=\left(-\widehat{\rho }\frac{dz}{dt}+\widehat{k}\frac{d\rho }{dt}\right)\frac{{\mu }_{0}i}{2\pi \rho }q}$

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}m\overrightarrow{a}=\overrightarrow{F},\{\begin{array}{l}\frac{d^2\rho }{d{t}^2}-\rho {\left(\frac{d\phi }{dt}\right)}^2=-\alpha \frac{1}{\rho }\frac{dz}{dt}\\ \rho \frac{d^2\phi }{d{t}^2}+2\frac{d\rho }{dt}\frac{d\phi }{dt}=0\\ \frac{d^{2}z}{d{t}^2}=\alpha \frac{1}{\rho }\frac{d\rho }{dt}\end{array}\\ \alpha =\frac{{\mu }_{0}i}{2\pi }\frac{q}{m}\end{array}}$

Constantes del movimiento

• Movimiento en la dirección \widehat{\phi }

Multiplicando la segunda ecuación por ρ, obtenemos una constante del movimiento

${\displaystyle \begin{array}{l}{\rho }^2\frac{d^2\phi }{d{t}^2}+2\rho \frac{d\rho }{dt}\frac{d\phi }{dt}=\frac{d}{dt}\left({\rho }^2\frac{d\phi }{dt}\right)=0\\ {\rho }^2\frac{d\phi }{dt}=\frac{L_z}{m}\end{array}}$

L_z es la componente Z del momento angular

• Movimiento a lo largo del eje Z

Integramos la tercera ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{dz}{dt}\right)=\alpha \frac{d}{dt}\ln \rho \\ \frac{dz}{dt}=\alpha \ln \rho +\text{cte}\\ \frac{dz}{dt}=\alpha \ln \left(\frac{\rho }{{\rho }_0}\right)\end{array}}$

Denominamos ρ₀ a esta constante del movimiento

• Movimiento en la dirección radial

Dado que la fuerza que ejerce un campo magnético sobre una partícula cargada es perpendicular a la velocidad. La energía cinética de la partícula se mantiene constante.

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}m{v}^2=\frac{1}{2}m\overrightarrow{v}·\overrightarrow{v}\\ \frac{d{E}_k}{dt}=m\left(\overrightarrow{v}\frac{d\overrightarrow{v}}{dt}\right)\\ \overrightarrow{F}=m\frac{d\overrightarrow{v}}{dt}=q\left(\overrightarrow{v}\times \overrightarrow{B}\right)\\ \frac{d{E}_k}{dt}=q\overrightarrow{v}·\left(\overrightarrow{v}\times \overrightarrow{B}\right)=0\end{array}}$

El producto escalar de dos vectores perpendiculares es nulo. La energía cinéica E_k es constante. La energía de la partícula cargada es

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}^2=\frac{1}{2}m\left({\left(\frac{d\rho }{dt}\right)}^2+{\rho }^2{\left(\frac{d\phi }{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)=\\ \frac{1}{2}m{\left(\frac{d\rho }{dt}\right)}^2+\frac{L_z^2}{2m}\frac{1}{{\rho }^2}+\frac{1}{2}m{\left(\alpha \ln \left(\frac{\rho }{{\rho }_0}\right)\right)}^2\end{array}}$

La partícula se mueve en la dirección radial, en un potencial

${\displaystyle E_p(\rho )=\frac{L_z^2}{2m}\frac{1}{{\rho }^2}+\frac{1}{2}m{\alpha }^2{\left(\ln \left(\frac{\rho }{{\rho }_0}\right)\right)}^2}$

Representamos la energía potencial E_p(ρ)



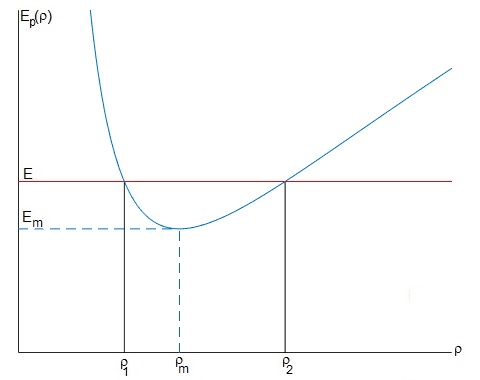
La energía potencial presenta un mínimo en ρ_m

${\displaystyle \begin{array}{l}\frac{d{E}_p(\rho )}{d\rho }=0\\ -\frac{L_z^2}{m{\rho }^3}+m{\alpha }^2\frac{1}{\rho }\ln \left(\frac{\rho }{{\rho }_0}\right)=0\end{array}}$

Obtenemos una ecuación transcendente en ρ

${\displaystyle {\left(\frac{L_z}{m\alpha \rho }\right)}^2=\ln \left(\frac{\rho }{{\rho }_0}\right)}$

cuya raíz es ρ_m que se obtiene mediante la función fzero de MATLAB

Siempre que la energía E de la partícula sea mayor que la mínima, E_m=E_p(ρ_m), la partícula oscila entre las posiciones ρ₁ y ρ₂, soluciones de la ecuación transcendente

E_p(ρ)-E=0

El código para representar parte de la figura es

Lz=1; %momento angular Z
m=1; %masa
alfa=1; %parámetro
rho_0=1; %parámetro
f=@(x) Lz^2./(2*m*x.^2)+m*alfa^2*(log(x/rho_0)).^2/2; %energía potencial
g=@(x) log(x/rho_0)-(Lz/(m*alfa*x))^2;
rho_m=fzero(g,[0.5,5]); %mínimo
E=1;
h=@(x) f(x)-E;
rho_1=fzero(h,[0.5,rho_m]); %retorno
rho_2=fzero(h,[rho_m, 5]); %retorno
hold on
Em=f(rho_m); %energía mínima
line([rho_m, rho_m],[0,Em],'lineStyle','--')
line([0, rho_m],[Em,Em],'lineStyle','--')
line([rho_1, rho_1],[0,f(rho_1)],'color','k')
line([rho_2, rho_2],[0,f(rho_2)],'color','k')
line([0, 3],[E,E],'color','r')
fplot(f,[0.5,3])
hold off
grid on
ylim([0,2])
xlabel('\rho')
ylabel('E_p')
title('Energía potencial')

El periodo de las oscilaciones en la dirección radial es el doble del tiempo que la partícula tarda en desplazarse desde ρ₁ a ρ₂

${\displaystyle \begin{array}{l}\frac{d\rho }{dt}=\sqrt{2\frac{E}{m}-\frac{L_z^2}{m^2}\frac{1}{{\rho }^2}-{\left(\alpha \ln \left(\frac{\rho }{{\rho }_0}\right)\right)}^2}\\ P=2{\displaystyle \underset{{\rho }_1}{\overset{{\rho }_2}{\int }}\frac{d\rho }{\sqrt{\frac{2E}{m}-{\left(\frac{L_z}{m\rho }\right)}^2-{\left(\alpha \ln \left(\frac{\rho }{{\rho }_0}\right)\right)}^2}}}\end{array}}$

Para amplitudes pequeñas de las oscilación, aproximamos la energía potencial

${\displaystyle E_p(\rho )=E_p({\rho }_m)+\frac{1}{2}{\left(\frac{d^2{E}_p}{d{\rho }^2}\right)}_{{\rho }_m}{\left(\rho -{\rho }_m\right)}^2+\mathrm{...}\approx E_p({\rho }_m)+\frac{1}{2}k{\left(\rho -{\rho }_m\right)}^2}$

La constante k=mω² del muelle elástico equivalente es

${\displaystyle k={\frac{d^2{E}_p(\rho )}{d{\rho }^2}|}_{{\rho }_m}=3\frac{L_z^2}{m{\rho }_m^4}-m{\alpha }^2\frac{1}{{\rho }_m^2}\ln \left(\frac{{\rho }_m}{{\rho }_0}\right)+m{\alpha }^2\frac{1}{{\rho }_m^2}=2\frac{L_z^2}{m{\rho }_m^4}+m{\alpha }^2\frac{1}{{\rho }_m^2}}$

La frecuencia angular ω es

${\displaystyle \omega =\sqrt{\frac{k}{m}}k=\sqrt{\frac{2L_z^2}{m^2{\rho }_m^4}+\frac{{\alpha }^2}{{\rho }_m^2}}=\frac{\alpha }{{\rho }_m}\sqrt{2\ln \left(\frac{{\rho }_m}{{\rho }_0}\right)+1}}$

El periodo es P=2π/ω

Añadimos al script anterior este código, para calcular el periodo

...
f=@(x) 1./sqrt(2*E/m-(Lz./(m*x)).^2-(alfa*log(x/rho_0)).^2);
P=2*integral(f, rho_1,rho_2); %periodo
w=alfa*sqrt(2*log(rho_m/rho_0)+1)/rho_m; %frecuencia angular
disp([P, 2*pi/w])

    4.8790    4.3439

El periodo exacto es 4.8790 y el aproximado (oscilaciones de pequeña amplitud) 4.3439

Velocidad de deriva

Se denomina velocidad de deriva, a la razón del desplazamiento a lo largo del eje Z durante un periodo P de oscilación

${\displaystyle \begin{array}{l}{v}_d=\frac{\Delta z}{P}=\frac{2\left(z_2-z_1\right)}{P}=\frac{2}{P}{\displaystyle \underset{{\rho }_1}{\overset{{\rho }_2}{\int }}\frac{dz}{d\rho }d\rho }=\frac{2}{P}{\displaystyle \underset{{\rho }_1}{\overset{{\rho }_2}{\int }}\frac{\frac{dz}{dt}}{\frac{d\rho }{dt}}d\rho }=\\ \frac{2\alpha }{P}{\displaystyle \underset{{\rho }_1}{\overset{{\rho }_2}{\int }}\frac{\ln \left(\frac{\rho }{{\rho }_0}\right)}{\sqrt{\frac{2E}{m}-{\left(\frac{L_z}{m\rho }\right)}^2-{\left(\alpha \ln \left(\frac{\rho }{{\rho }_0}\right)\right)}^2}}d\rho }\end{array}}$

Trayectorias

Para representar la trayectoria hay que integrar las ecuaciones del movimiento

${\displaystyle \{\begin{array}{l}\frac{d^2\rho }{d{t}^2}=\rho {\left(\frac{d\phi }{dt}\right)}^2-\frac{\alpha }{\rho }\frac{dz}{dt}\\ \frac{d^2\phi }{d{t}^2}=-\frac{2}{\rho }\frac{d\rho }{dt}\frac{d\phi }{dt}\\ \frac{d^{2}z}{d{t}^2}=\frac{\alpha }{\rho }\frac{d\rho }{dt}\end{array}}$

Con las siguientes condiciones iniciales

La partícula parte t=0, de una posición que dista ρ(0) de la corriente rectilínea (eje Z). Tomamos el ángulo φ(0)=0 y z(0)=0

Las componentes de la velocidad inicial, vienen determinadas por las constantes del movimiento (L_z, ρ₀, E) y el parámetro α

${\displaystyle t=0\{\begin{array}{l}\frac{d\rho }{dt}=\sqrt{2\frac{E}{m}-{\left(\frac{L_z}{m\rho }\right)}^2-{\left(\alpha \ln \left(\frac{\rho }{{\rho }_0}\right)\right)}^2}\\ \frac{d\phi }{dt}=\frac{L_z}{m}\frac{1}{{\rho }^2}\\ \frac{dz}{dt}=\alpha \ln \left(\frac{\rho }{{\rho }_0}\right)\end{array}}$

Representamos la trayectoria de la partícula cargada para los siguientes valores

• Componente Z del momento angular, L_z=1
• Masa de la partícula, m=1
• Parámetro, α=1
• Constante, ρ₀=0.5
• Energía de la partícula, E=1
• Distancia inicial de la partícula a la corriente rectilínea (eje Z), ρ(0)=1

Lz=1; %momento angular Z
m=1; %masa
alfa=1; %parámetro
rho_0=0.5; %parámetro
E=1; %energía
f=@(t,x) [x(2); x(1)*x(4)^2-alfa*x(6)/x(1); x(4); -2*x(2)*x(4)/x(1);
 x(6); alfa*x(2)/x(1)];
r_0=1; %distancia radial inicial
%componentes de la velocidad inicial
vr=sqrt(2*E/m-(Lz/(m*r_0))^2-(alfa*log(r_0/rho_0))^2);
vphi=Lz/(m*r_0^2);
vz=alfa*log(r_0/rho_0);
[t,x]=ode45(f,[0,25],[r_0,vr, 0, vphi, 0,vz]);
plot3(x(:,1).*cos(x(:,3)),x(:,1).*sin(x(:,3)),x(:,5))
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Trayectoria')

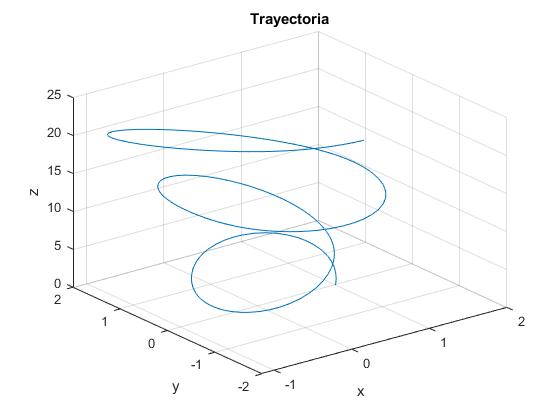
Casos particulares

• Cuando la energía de la partícula E coincide con el mínimo E=E_p(ρ_m)

La distancia radial ρ_m permanece constante. La trayectoria de la partícula es una hélice

Lz=1; %momento angular Z
m=1; %masa
alfa=1; %parámetro
rho_0=0.5; %parámetro
f=@(x) Lz^2./(2*m*x.^2)+m*alfa^2*(log(x/rho_0)).^2/2; %energía potencial
g=@(x) log(x/rho_0)-(Lz/(m*alfa*x))^2;
rho_m=fzero(g,[0.5,5]); %mínimo
E=f(rho_m); %energía mínima
r_0=rho_m; %distancia radial inicial
%componentes de la velocidad inicial
vr=0;
vphi=Lz/(m*r_0^2);
vz=alfa*log(r_0/rho_0);
f=@(t,x) [x(2); x(1)*x(4)^2-alfa*x(6)/x(1); x(4); -2*x(2)*x(4)/x(1); 
x(6); alfa*x(2)/x(1)];
[t,x]=ode45(f,[0,25],[r_0,vr, 0, vphi, 0,vz]);
plot3(x(:,1).*cos(x(:,3)),x(:,1).*sin(x(:,3)),x(:,5))
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Trayectoria')



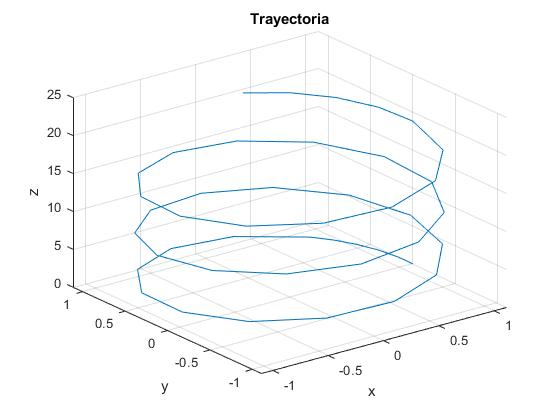
• Cuando la componente L_z del momento angular es nula

Entonces φ=cte. La trayectoria está contenida en el plano XZ (φ=0)

Se resuelven las ecuaciones del movimiento

${\displaystyle \{\begin{array}{l}\frac{d^2\rho }{d{t}^2}=-\frac{\alpha }{\rho }\frac{dz}{dt}\\ \frac{d^{2}z}{d{t}^2}=\frac{\alpha }{\rho }\frac{d\rho }{dt}\end{array}}$

con las condiciones iniciales:

La partícula parte t=0, de una posición que dista ρ(0) del eje Z. Tomamos z(0)=0

${\displaystyle t=0\{\begin{array}{l}\frac{d\rho }{dt}=\sqrt{2\frac{E}{m}-{\left(\alpha \ln \left(\frac{\rho }{{\rho }_0}\right)\right)}^2}\\ \frac{dz}{dt}=\alpha \ln \left(\frac{\rho }{{\rho }_0}\right)\end{array}}$

m=1; %masa
alfa=1; %parámetro
rho_0=0.5; %parámetro
E=1; %energía 
f=@(t,x) [x(2); -alfa*x(4)/x(1); x(4); alfa*x(2)/x(1)];
r_0=1; 
z_0=0;
vr=sqrt(2*E/m-(alfa*log(r_0/rho_0))^2);
vz=alfa*log(r_0/rho_0);
[t,x]=ode45(f,[0,15],[r_0,vr, z_0,vz]);
plot(x(:,1),x(:,3))
grid on
xlabel('x')
ylabel('z')
title('Trayectoria')

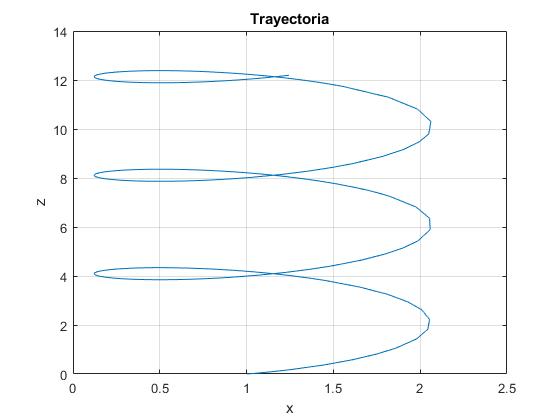
Referencias

Joel Franklin, David J. Griffiths, Nelia Mann. Motion of a charged particle in the static fields of an infinite straight wire. Am. J. Phys. 90 (7), July 2022. pp. 513-519