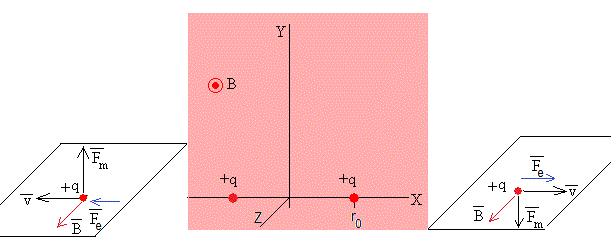
Como vemos en la figura, las fuerzas de repulsión eléctrica, $\overrightarrow{F_e}$ son iguales y opuestas. Cuando se liberan las partículas de su posición inicial, se mueven a lo largo del eje X, y actúa la fuerza magnética, $\overrightarrow{F_m}=q\overrightarrow{v}\times \overrightarrow{B}$

La fuerza que ejerce el campo magnético, $\overrightarrow{F_m}$ sobre cada una de las cargas en movimiento son iguales y opuestas. Si la partícula de la derecha se encuentra en el instante t en la posición (x,y), la partícula de la izquierda se encontrará en el mismo instante en la posición (-x,-y). El origen O es centro de simetría y por tanto, la línea que une ambas partículas pasa por el origen. Debido a esta simetría solamente precisaremos calcular la trayectoria de una de las partículas, la que está a la derecha del origen.

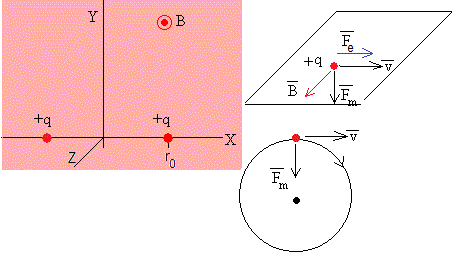
Comparamos un sistema formado por dos cargas positivas (en rojo) y el formado por dos cargas negativas (en azul), vemos que la fuerza eléctrica es la misma, y la fuerza magnética cambia de signo. De modo que, la carga positiva y la carga negativa describen trayectorias similares, simétricas respecto del eje X, la carga positiva recorrerá la trayectoria en el sentido de las agujas del reloj y la negativa en el sentido contrario.

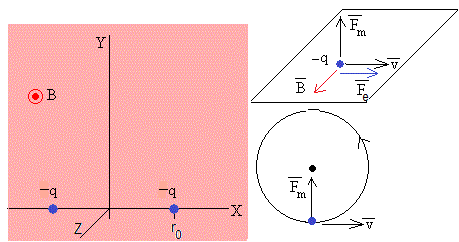
Deduciremos la ecuación de la trayectoria suponiendo que las dos cargas son positivas

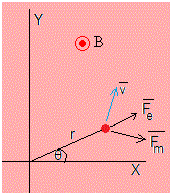
Analizamos el movimiento de la partícula cargada positivamente situada en el instante t=0 en la posición (r₀,0)

La fuerza de repulsión eléctrica entre las dos cargas tiene dirección radial y vale

${\displaystyle \overrightarrow{F_e}=\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{{\left(2r\right)}^2}\widehat{r}}$

El campo magnético, paralelo al eje Z, $\overrightarrow{B}=B\widehat{k}$, ejerce una fuerza sobre la partícula cargada en movimiento con velocidad v

Teniendo en cuenta los productos de los vectores unitarios $\widehat{r}\times \widehat{k}=-\widehat{\theta },\widehat{\theta }\times \widehat{k}=\widehat{r}$. Además, en este problema, es conveniente expresar la velocidad y aceleración en coordenadas polares (al final de esta página)

${\displaystyle \overrightarrow{F_m}=q\overrightarrow{v}\times \overrightarrow{B}=qB\overrightarrow{v}\times \widehat{k}=qB\left(\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\right)\times \widehat{k}=qB\left(r\frac{d\theta }{dt}\widehat{r}-\frac{dr}{dt}\widehat{\theta }\right)}$

Las ecuaciones del movimiento son

${\displaystyle m\overrightarrow{a}=\overrightarrow{F_e}+\overrightarrow{F_m}\{\begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{{\left(2r\right)}^2}+qBr\frac{d\theta }{dt}\\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)=-qB\frac{dr}{dt}\end{array}}$

Se resuelve el sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales.

${\displaystyle t=0\{\begin{array}{l}r=r_0\frac{dr}{dt}=0\\ \theta =0\frac{d\theta }{dt}=0\end{array}}$

Este es el planteamiento del problema sugerido por el primer artículo citado en las referencias. El que se va a dar a continuación es el de un sistema de dos partículas interactuantes que se estudia en la página titulada Movimiento del c.m. y de las partículas de un sistema (I) y posteriores. Dividiremos el problema en dos partes:

• Movimiento del centro de masas del sistema de dos partículas

• Movimiento relativo de las dos partículas

Sistema de dos partículas

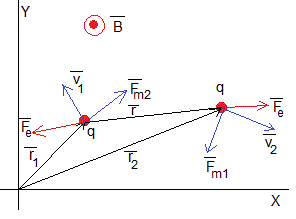
En la figura, se muestran dos cargas iguales +q, de la misma masa m, cuyas posiciones en el instante t son $\overrightarrow{r_1}$ y $\overrightarrow{r_2}$

Las fuerzas de repulsión eléctrica, son iguales y opuestas.

${\displaystyle \begin{array}{l}\overrightarrow{F_e}=\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r^2}\widehat{r}\\ \overrightarrow{r}=\overrightarrow{r_2}-\overrightarrow{r_1}\end{array}}$

Donde $\overrightarrow{r}$ es el vector posición relativa

La fuerza magnética, $\overrightarrow{F_m}=q\overrightarrow{v}\times \overrightarrow{B}$ es perpendicular al producto vectorial de la velocidad de la partícula y del campo magnético, cuya dirección es el eje Z, $\overrightarrow{B}=B\widehat{k}$

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}m\frac{d^2\overrightarrow{r_1}}{d{t}^2}=-\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r^2}\widehat{r}+q\frac{d\overrightarrow{r_1}}{dt}\times \overrightarrow{B}\\ m\frac{d^2\overrightarrow{r_2}}{d{t}^2}=\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r^2}\widehat{r}+q\frac{d\overrightarrow{r_2}}{dt}\times \overrightarrow{B}\end{array}}$

• Ecuación del movimiento del centro de masas

Sumamos las ecuaciones

${\displaystyle \begin{array}{l}m\frac{d^2\left(\overrightarrow{r_1}+\overrightarrow{r_2}\right)}{d{t}^2}=q\frac{d\left(\overrightarrow{r_1}+\overrightarrow{r_2}\right)}{dt}\times \overrightarrow{B}\\ m\frac{d^2\overrightarrow{R}}{d{t}^2}=q\frac{d\overrightarrow{R}}{dt}\times \overrightarrow{B}\\ \overrightarrow{R}=\frac{\overrightarrow{r_1}+\overrightarrow{r_2}}{2}\end{array}}$



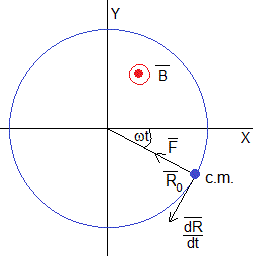
El centro de masas describe una trayectoria circular de radio R₀ centrada en el origen, con velocidad angular ω. Escribimos la ecuación de la dinámica del movimiento circular uniforme

${\displaystyle \begin{array}{l}m\frac{V^2}{R_0}=qVB\sin 90\\ \omega =\frac{V}{R_0}=\frac{qB}{m}\end{array}}$

Siendo V=dR/dt la velocidad del centro de masas

El periodo P o tiempo que trda en dar una vuelta es

${\displaystyle P=\frac{2\pi }{\omega }=\frac{2\pi m}{qB}}$

La posición del centro de masas en función del tiempo es

${\displaystyle \overrightarrow{R}=R_0\cos \left(\omega t\right)\widehat{i}-R_0\sin \left(\omega t\right)\widehat{j}}$

• Ecuación del movimiento relativo de las dos partículas

Restamos las dos ecuaciones del movimiento y obtenemos la ecuación del movimiento relativo de las dos partículas

${\displaystyle \begin{array}{l}m\frac{d^2\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right)}{d{t}^2}=2\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r^2}\widehat{r}+q\frac{d\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right)}{dt}\times \overrightarrow{B}\\ m\frac{d^2\overrightarrow{r}}{d{t}^2}=2\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r^2}\widehat{r}+q\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{B}\\ m\overrightarrow{a}=2\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r^2}\widehat{r}+q\overrightarrow{v}\times \overrightarrow{B}\end{array}}$

Expresamos la velocidad relativa $\overrightarrow{v}$ y la aceleración relativa $\overrightarrow{a}$, en coordenadas polares (al final de esta página). Teniendo en cuenta los productos de los vectores unitarios $\widehat{r}\times \widehat{k}=-\widehat{\theta },\widehat{\theta }\times \widehat{k}=\widehat{r}$, obtenemos un sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}m\left\{\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\right\}=2\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r^2}\widehat{r}+q\left\{\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\right\}\times B\widehat{k}\\ \{\begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=2\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r^2}+qBr\frac{d\theta }{dt}\\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)=-qB\frac{dr}{dt}\end{array}\end{array}}$

Estudiamos la segunda ecuación diferencial

${\displaystyle \begin{array}{l}m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)=-qB\frac{dr}{dt}\\ \frac{d}{dt}\left(r^2\frac{d\theta }{dt}\right)=-\frac{qB}{2m}\frac{d}{dt}{r}^2\\ \frac{d}{dt}\left(r^2\left(\frac{d\theta }{dt}+\frac{qB}{2m}\right)\right)=0\\ m{r}^2\left(\frac{d\theta }{dt}+\frac{\omega }{2}\right)=L_{\omega }=\text{cte}\end{array}}$

Obtenemos una constante del movimiento que denominamos L_ω y que se determina a partir de las condiciones iniciales, de r y dθ/dt en el instante t=0

Estudiamos la primera ecuación diferencial, en la dirección radial, en la que se sustituye dθ/dt por las constantes L_ω y ω

${\displaystyle m\frac{d^{2}r}{d{t}^2}=\frac{L_{\omega }^2}{m{r}^3}-mr\frac{{\omega }^2}{4}+2\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r^2}}$

Resolvemos el sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales: t=0, r=r₀, θ=0, dr/dt=0, dθ/dt=0.

Para estas condiciones iniciales, la primera ecuación diferencial se escribe

${\displaystyle \begin{array}{l}{L}_{\omega }=m{r}_0^2\frac{\omega }{2}\\ \frac{d\theta }{dt}=\frac{\omega }{2}\left(\frac{r_0^2}{r^2}-1\right)\end{array}}$

Escalas

Definimos las variables adimensionales

${\displaystyle x=\frac{r}{r_0},\tau =\frac{t}{P}=t\frac{qB}{2\pi m}}$

Siendo P el periodo o tiempo que tarda una carga en dar una vuelta cuando describe una trayectoria circular en un campo magnético uniforme.

${\displaystyle \begin{array}{l}\frac{d\theta }{d\tau }=\pi \left(\frac{1}{x^2}-1\right)\\ \frac{d^{2}x}{d{\tau }^2}={\pi }^2\left(\frac{1}{x^3}-x+\frac{4}{x^2}c\right),c=\frac{1}{4\pi {\epsilon }_0}\frac{2m}{B^2{r}_0^3}\end{array}}$

Para describir el movimiento relativo de las dos partículas se resuelve el sistema de dos ecuaciones diferenciales, con las condiciones iniciales, τ=0, x=1, dx/dτ=0, θ=0, dθ/dt=0.

Trayectoria

Si integramos la segunda ecuación diferencial, en la dirección radial

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{\tau }^2}=\frac{du}{d\tau }=u\frac{du}{dx}\\ u\frac{du}{dx}={\pi }^2\left(\frac{1}{x^3}-x+\frac{4c}{x^2}\right)\\ u^2={\pi }^2{\displaystyle \underset{1}{\overset{x}{\int }}\left(\frac{1}{z^3}-z+\frac{4c}{z^2}\right)}dz\\ u^2={\pi }^2\left(8c\left(1-\frac{1}{x}\right)-{\left(x-\frac{1}{x}\right)}^2\right)\\ u^2={\pi }^2\frac{x-1}{x^2}\left(8cx-{\left(x+1\right)}^2(x-1)\right)\end{array}}$

La velocidad radial se anula u=0, para x=1 y para otro valor máximo de x, solución de la ecuación cúbica

(x+1)²(x-1)-8cx=0
x³+x²-(1+8c)x-1=0

Denominamos x_máx a la raíz real positiva de esta ecuación.

>> c=1/8;
>> roots([1,1,-(1+8*c),-1]);
ans =
   -1.8019
    1.2470
   -0.4450

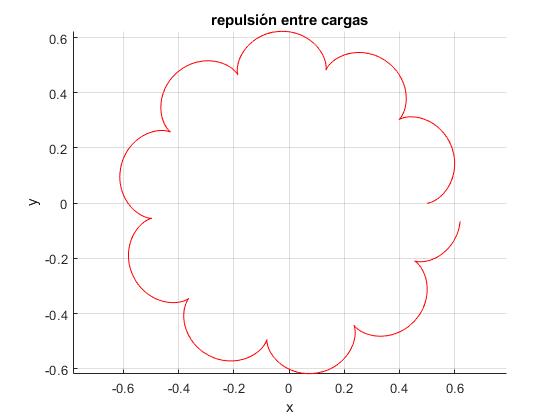
La separación entre las dos partículas oscila entre un máximo de 1.247 y un mínimo de 1.

Como se ha hecho en dinámica celeste, para determinar la ecuación de la trayectoria despejamos dθ/dx e integramos

${\displaystyle \begin{array}{l}u=\frac{dx}{d\tau }=\frac{dx}{d\theta }\frac{d\theta }{d\tau }\\ \frac{d\theta }{dx}=\frac{1}{u}\frac{d\theta }{d\tau }\\ \theta ={\displaystyle \underset{1}{\overset{x}{\int }}\frac{\pi \left(\frac{1}{z^2}-1\right)}{\frac{\pi }{z}\sqrt{(z-1)\left(8cz-{\left(z+1\right)}^2(z-1)\right)}}dz}\\ \theta =-{\displaystyle \underset{1}{\overset{x}{\int }}\frac{z+1}{z}\sqrt{\frac{z-1}{8cz-{\left(z+1\right)}^2\left(z-1\right)}}dz},x\le x_{max}\end{array}}$

Cuando el límite superior de la integral es x_máx, (raíz positiva de la ecuación cúbica), obtenemos el ángulo θ_máx.

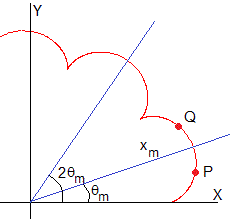
La ecuación implícita solamente calcula la parte de trayectoria comprendida entr 0 y θ_máx, el resto de la trayectoria como se muestra en la figura se traza de la siguiente manera:

La recta que pasa por el origen y forma un ángulo θ_máx es un eje de simetría. El punto Q es simétrico de P. Si las coordenadas de P son (x, θ) las coordenadas de Q son (x, 2θ_máx-θ)

La recta que pasa por el origen y forma un ángulo 2θ_máx es un eje de simetría. Si las coordendas de un punto son (x, θ) las coordenadas de su simétrico serán (x, 4θ_máx-θ) y así, sucesivamente

Elaboramos el siguiente script para dibujar la trayectoria

c=1/8; %parámetro
%calcula la raíz real positiva
 ra=roots([1,1,-(1+8*c),-1]);
 for i=1:3
     if ra(i)>0
         break;
     end
 end
s_m=ra(i);
f=@(x) (x+1).*sqrt((x-1)./(8*c*x-((x+1).^2).*(x-1)))./x;
fi_m=integral(f,1,s_m);
%trayectoria implícita
ss=linspace(1,s_m,100);
fi=zeros(1,length(ss));
i=1;
for s=ss
    fi(i)=integral(f,1,s);
    i=i+1;
end
hold on
plot(ss.*cos(fi)/2,ss.*sin(fi)/2,'r')

N=round(2*pi/fi_m);
for n=2:2:N %simetría
    plot(ss.*cos(n*fi_m-fi)/2,ss.*sin(n*fi_m-fi)/2,'r')
    plot(ss.*cos(n*fi_m+fi)/2,ss.*sin(n*fi_m+fi)/2,'r')
end
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('repulsión entre cargas')

Energía

La fuerza magnética es perpendicular a la velocidad de la partícula cargada por lo que no realiza trabajo. La energía en el S.R. del centro de masa es

${\displaystyle \begin{array}{l}E=\frac{1}{2}\frac{m}{2}{v}^2+\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r}=\frac{1}{4}m\left({\left(\frac{dr}{dt}\right)}^2+{\left(r\frac{d\theta }{dt}\right)}^2\right)+\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r}=\\ \frac{1}{4}m\left({\left(\frac{dr}{dt}\right)}^2+{\left(r\frac{\omega }{2}\left(\frac{r_0^2}{r^2}-1\right)\right)}^2\right)+\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{r}\end{array}}$

Donde m/2 es la masa reducida

En términos de las variables adimensionales x y τ

${\displaystyle \begin{array}{l}E\frac{4m}{r_0^2{q}^2{B}^2}=\frac{1}{4}\left(\frac{1}{{\pi }^2}{\left(\frac{dx}{d\tau }\right)}^2+x^2{\left(\frac{1}{x^2}-1\right)}^2\right)+\frac{4m}{r_0^2{B}^2}\frac{1}{4\pi {\epsilon }_0}\frac{1}{x}\\ \epsilon =\frac{1}{4}\left(\frac{1}{{\pi }^2}{\left(\frac{dx}{d\tau }\right)}^2+x^2{\left(\frac{1}{x^2}-1\right)}^2\right)+\frac{2c}{x}\end{array}}$

La energía ε se mantiene constante en el S. R. del centro de masas e igual a la energía inicial, cuando τ=0, x=1, dx/dτ=0, ε=2c

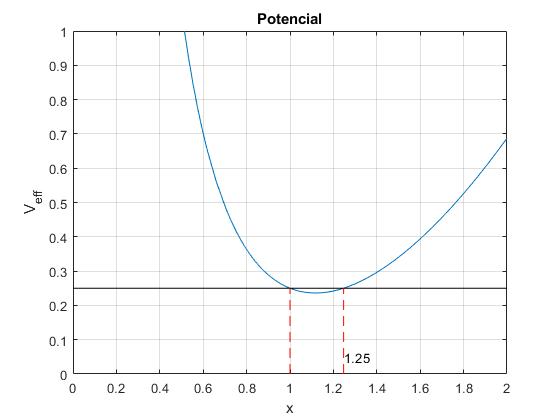
Representamos el potencial efectivo V_eff(x) y la energía constante ε=2c

${\displaystyle V_{eff}(x)=\frac{1}{4}{x}^2{\left(\frac{1}{x^2}-1\right)}^2+\frac{2c}{x}}$

Calculamos la distancia máxima, (la mínima es (x=1), entre las dos partículas, cuando ε=V_eff(x)

${\displaystyle 2cx(x-1)-\frac{1}{4}{\left(x^2-1\right)}^2=0}$

c=1/8;  %parámetro
E=2*c; %energía inicial
f=@(x) 2*c./x+(x.^2).*(1./x.^2-1).^2/4;
fplot(f,[0.1,2])
line([0,2],[E,E],'color','k')
raices= roots([1,1,-(1+8*c),-1]);
x1=1;
for i=1:length(raices)
    if raices(i)>0
        x2=raices(i);
    end
end
line([x1,x1],[0,f(x1)],'lineStyle','--','color','r')
line([x2,x2],[0,f(x2)],'lineStyle','--','color','r')
%text(x1,0.05,sprintf('%1.2f',x1))
text(x2,0.05,sprintf('%1.2f',x2))
grid on
ylim([0,1])
xlabel('x')
ylabel('V_{eff}')
title('Potencial')

Movimiento respecto del S.R. inercial

Conocido el movimiento relativo de las dos partículas y el movimiento del centro de masas, determinamos el movimiento de cada una de las dos partículas

${\displaystyle \begin{array}{l}\{\begin{array}{l}\overrightarrow{R}=\frac{\overrightarrow{r_1}+\overrightarrow{r_2}}{2}\\ \overrightarrow{r}=\overrightarrow{r_2}-\overrightarrow{r_1}\end{array}\{\begin{array}{l}\overrightarrow{r_2}=\overrightarrow{R}+\frac{1}{2}\overrightarrow{r}\\ \overrightarrow{r_1}=\overrightarrow{R}-\frac{1}{2}\overrightarrow{r}\end{array}\\ \{\begin{array}{l}\frac{\overrightarrow{r_2}}{r_0}=\frac{R_0}{r_0}\left(\cos \left(2\pi \tau \right)\widehat{i}-\sin \left(2\pi \tau \right)\widehat{j}\right)+\frac{x}{2}\left(\cos \theta \widehat{i}+\sin \theta \widehat{j}\right)\\ \frac{\overrightarrow{r_1}}{r_0}=\frac{R_0}{r_0}\left(\cos \left(2\pi \tau \right)\widehat{i}-\sin \left(2\pi \tau \right)\widehat{j}\right)-\frac{x}{2}\left(\cos \theta \widehat{i}+\sin \theta \widehat{j}\right)\end{array}\end{array}}$

El caso más sencillo, el centro de masas está en reposo en el origen R₀=0. Se representan las trayectorias de las dos partículas para c=1/8. Comprobamos la separación máxima y mínima entre las dos partículas

c=1/8;  %parámetro
rR=0; %cociente R0/r0
%x(1) es x, x(2) es dx/dtau y x(3) es th
f=@(t,x) [x(2); pi^2*(1/x(1)^3-x(1)+4*c/x(1)^2);pi*(1/x(1)^2-1);];
[t,x]=ode45(f,[0,10],[1,0,0]);
hold on
x1=rR*cos(2*pi*t)+x(:,1).*cos(x(:,3))/2; %rR*cos(2*pi*t)+
y1=-rR*sin(2*pi*t)+x(:,1).*sin(x(:,3))/2; %-rR*sin(2*pi*t)
plot(x1,y1)
x2=rR*cos(2*pi*t)-x(:,1).*cos(x(:,3))/2; %rR*cos(2*pi*t)+
y2=-rR*sin(2*pi*t)-x(:,1).*sin(x(:,3))/2; %-rR*sin(2*pi*t)
plot(x2,y2)
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Trayectoria')

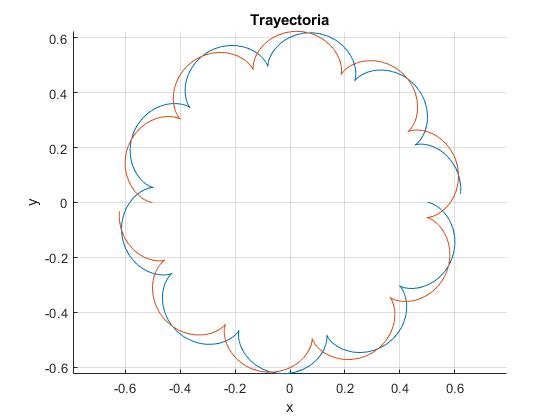
La separación máxima y mínima entre las dos partículas es

>> d=sqrt((x1-x2).^2+(y1-y2).^2);
>> max(d)
ans =    1.2474
>> min(d)
ans =    0.9996

Comprobamos el principio de conservación de la energía en el S. R. del centro de masa

>> Eini=2*c;
>> Efin=(x(:,2).^2/pi^2+(x(:,1).^2).*(1./x(:,1).^2-1).^2)/4+2*c./x(:,1);
>> Eini,Efin
Eini =    0.2500
Efin =
    0.2500
    0.2500
    0.2500
    ...

Cambiamos el valor del parámetro c para dibujar otras trayectorias, por ejemplo para c=10/8

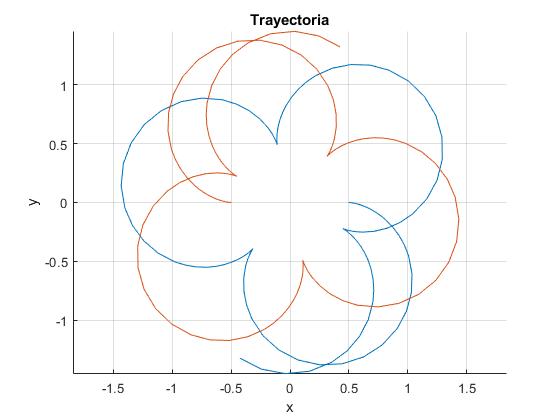
La separación máxima y mínima entre las dos partículas es

>> d=sqrt((x1-x2).^2+(y1-y2).^2);
>> max(d)
ans =    2.9066
>> min(d)
ans =     1
>> roots([1,1,-(1+8*c),-1]) %raíz positiva
ans =
    -3.8148
    2.9050
   -0.0902

Supongamos ahora que, el centro de masas describe una trayectoria circular de radio R₀/r₀=1. Dibujamos la trayectoria de una partícula

c=1/8;  %parámetro
rR=1; %cociente R0/r0
%x(1) es x, x(2) es dx/dtau y x(3) es th
f=@(t,x) [x(2); pi^2*(1/x(1)^3-x(1)+4*c/x(1)^2);pi*(1/x(1)^2-1);];
[t,x]=ode45(f,[0,10],[1,0,0]);
x1=rR*cos(2*pi*t)+x(:,1).*cos(x(:,3))/2; %rR*cos(2*pi*t)+
y1=-rR*sin(2*pi*t)+x(:,1).*sin(x(:,3))/2; %-rR*sin(2*pi*t)
plot(x1,y1)
grid on
axis equal
xlabel('x')
ylabel('y')
title('Trayectoria')

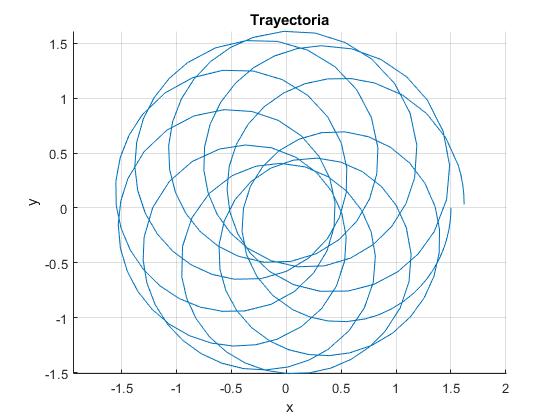
Cambiamos el valor del parámetro c para dibujar otras trayectorias, por ejemplo para c=10/8

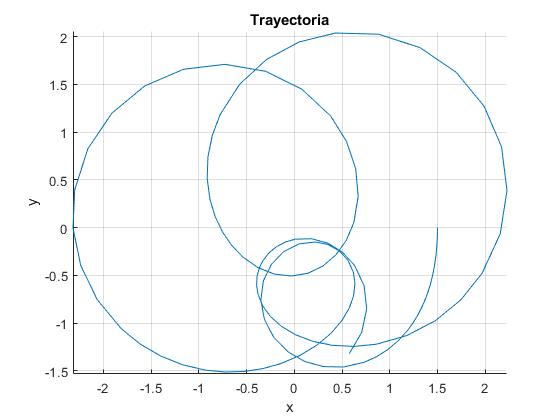
Un problema interesante, sería encontrar las condiciones para que las trayectorias sean cerradas y que se repitan cada cierto periodo de tiempo

Coordenadas polares

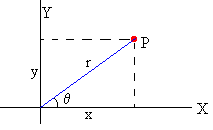
La posición de una partícula es (x, y) en coordenadas rectangulares y (r, θ) en coordenadas polares. La relación es

x=r·cosθ, y=r·sinθ

Expresamos la velocidad de la partícula en coordenadas polares

${\displaystyle \overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\widehat{r}\frac{dr}{dt}+r\frac{d\widehat{r}}{dt}}$

Calculamos las componentes rectangulares de los vectores unitarios $\widehat{r}$ y $\widehat{\theta }$

${\displaystyle \begin{array}{l}\widehat{r}=\widehat{i}\cos \theta +\widehat{j}\sin \theta \hfill \\ \widehat{\theta }=-\widehat{i}\sin \theta +\widehat{j}\cos \theta \hfill \end{array}}$

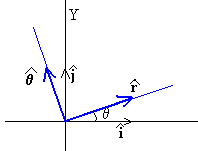
vemos que

${\displaystyle \begin{array}{l}\frac{d\widehat{r}}{dt}=(-\widehat{i}\sin \theta +\widehat{j}\cos \theta )\frac{d\theta }{dt}=\widehat{\theta }\frac{d\theta }{dt}\hfill \\ \frac{d\widehat{\theta }}{dt}=(-\widehat{i}\cos \theta -\widehat{j}\sin \theta )\frac{d\theta }{dt}=-\widehat{r}\frac{d\theta }{dt}\hfill \end{array}}$

Las expresión del vector velocidad en coordenadas polares es

${\displaystyle \overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }}$

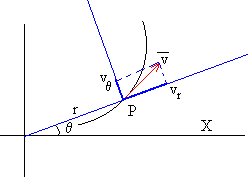
Las expresión del vector aceleración es:

${\displaystyle \begin{array}{l}\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\widehat{r}}{dt}+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }+r\frac{d\theta }{dt}\frac{d\widehat{\theta }}{dt}=\hfill \\ \frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }-r{\left(\frac{d\theta }{dt}\right)}^2\widehat{r}=\hfill \\ \left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\hfill \end{array}}$

Referencias

Carl E Mungan Orbits of two electrons released from rest in a uniform transverse magnetic field. Eur. J. Phys. 39 (2018) 025204

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017

O. L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Questions 10.16, 10.17, pp. 314-316