Movimiento de una partícula cargada que desliza a lo largo de un plano inclinado
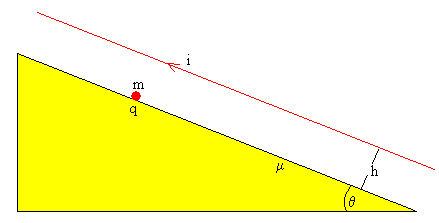
Una corriente rectilínea indefinida, de intensidad i, produce un campo magnético a una distancia h del hilo cuyo módulo es
Cuya dirección es perpendicular al plano determinado por la corriente rectilínea y la posición de la partícula (el plano del dibujo) y cuyo sentido viene determinado por la regla de la mano derecha. El campo magnético ejerce una fuerza sobre la partícula cargada en movimiento
Cuya dirección es perpendicular al plano inclinado.
La corriente circula en sentido hacia arriba
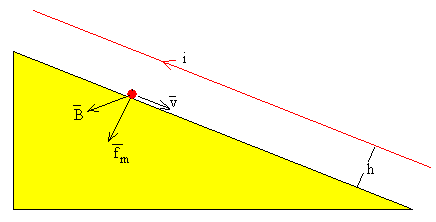
Las fuerzas sobre la partícula son:
- El peso, mg
- La fuerza que ejerce el campo magnético, fm=qvB
- La reacción del plano, N
- La fuerza de rozamiento que se opone al movimiento de la partícula, Fr=μN
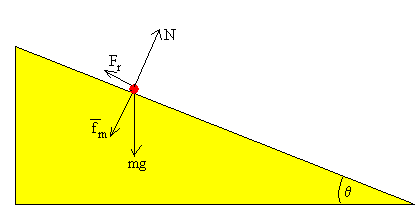
Descomponemos las fuerzas en la dirección del plano inclinado y en dirección perpendicular a dicho plano.
Aplicamos la condición de equilibrio en la dirección perpendicular al plano inclinado
N=qvB+mg·cosθ
Escribimos la ecuación del movimiento a lo largo del plano inclinado
ma=mg·sinθ-Fr
En forma de ecuación diferencial
Integramos la ecuación diferencial con la siguiente condición inicial: en el instante t=0, v=0, la partícula está en reposo.
La velocidad va creciendo hasta que alcanza un valor límite constante, cuando t→∞
Integramos de nuevo, para obtener la posición de la partícula en función del tiempo, supondremos que en el instante t=0, parte del origen x=0.
Se cambia de sentido a la corriente
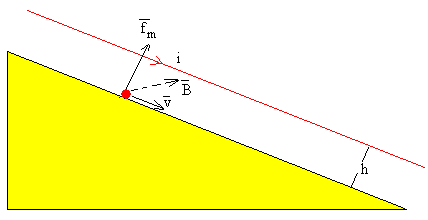
Las fuerzas sobre la partícula son:
- El peso, mg
- La fuerza que ejerce el campo magnético, fm=qvB, que cambia de sentido al cambiar el sentido del campo magnético.
- La reacción del plano, N
- La fuerza de rozamiento que se opone al movimiento de la partícula, Fr=μN
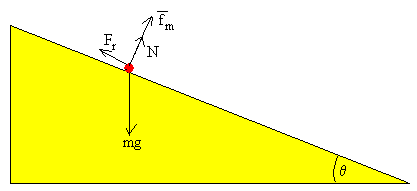
Descomponemos las fuerzas en la dirección del plano inclinado y en dirección perpendicular a dicho plano.
Aplicamos la condición de equilibrio en la dirección perpendicular al plano inclinado
N= mg·cosθ-qvB
Escribimos la ecuación del movimiento a lo largo del plano inclinado
ma=mg·sinθ-Fr
En forma de ecuación diferencial
Integramos la ecuación diferencial con la siguiente condición inicial: en el instante t=0, v=0, la partícula está en reposo.
Integramos de nuevo, para obtener la posición de la partícula en función del tiempo, supondremos que en el instante t=0, parte del origen x=0.
A medida que se incrementa la velocidad v, la reacción N del plano inclinado disminuye, para una velocidad vl la reacción se hace cero, N=0
o bien, en el instante
La partícula no desliza a lo largo del plano inclinado
A partir de dicho instante, las fuerzas sobre la partícula son
- El peso, mg
- La fuerza magnética, , que es perpendicular al vector velocidad
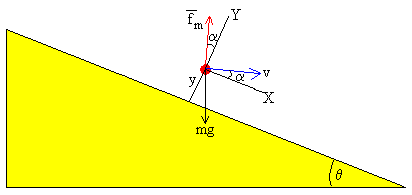
Establecemos de nuevo, los ejes a lo largo del plano inclinado, eje X, y perpendicular a dicho plano, eje Y. Las ecuaciones del movimiento son:
Donde B es el módulo del campo magnético producido por la corriente rectilínea en la posición que ocupa la partícula.
Si la ordenada de la partícula es y, (h-y) es la distancia de la corriente rectilínea a la partícula.
Se resuelve mediante procedimientos numéricos este sistema de dos ecuaciones diferenciales, con las siguientes condiciones iniciales, en el instante t=tl, la velocidad de la partícula es dx/dt=vl, dy/dt=0, y su posición es x= xl, y=0.
Actividades
Se introduce
- El ángulo θ del plano inclinado, en el control titulado Ángulo
- La intensidad i que circula por la corriente rectilínea, que puede se positiva o negativa, en el control titulado Intensidad. El sentido de la corriente se especifica mediante una flecha sobre la corriente rectilínea.
- La distancia de la corriente rectilínea al plano inclinado se ha fijado en h=0.25 m
- El coeficiente de rozamiento se ha fijado en μ=0.2
- La constante k se divide en dos factores
El primer factor p es proporcional a la relación entre la carga q y la masa m de la partícula. Este factor se puede cambiar en el control titulado Parámetro
Se pulsa el botón titulado Nuevo
Se observa el movimiento de la partícula cargada deslizando a lo largo del plano inclinado. Cuando la intensidad de la corriente es negativa, después de deslizar se eleva y describe una complicada trayectoria en las proximidades de la corriente rectilínea.
En la parte superior derecha, se proporcionan los datos del tiempo t, velocidad v, posición x, y reacción del plano inclinado N.
Ejemplo 1
- Intensidad de la corriente, i=40 A
- Ángulo del plano inclinado, θ=20º
- Parámetro, p=0.06
- Distancia a la corriente rectilínea, h=0.25 m
- El coeficiente de rozamiento, μ=0.2
Velocidad en función del tiempo
Al cabo de un cierto tiempo t=2 s la velocidad vale v=0.770 m/s
La velocidad límite cuando t→∞
La posición de la partícula en función del tiempo
En el instante t=2, x=1.17 m
Ejemplo 2
- Intensidad de la corriente, i=-20 A
- Ángulo del plano inclinado, θ=20º
- Parámetro, p=0.06
- Distancia a la corriente rectilínea, h=0.25 m
- El coeficiente de rozamiento, μ=0.2
La reacción N del plano va disminuyendo, hasta que se hace cero. La velocidad de la partícula vale.
En el instante
y en la posición
A partir de este instante, la partícula abandona el plano inclinado y se mueve bajo la acción de la fuerza magnética y del peso. Se calcula la posición de la partícula en función del tiempo, resolviendo un sistema de dos ecuaciones diferenciales de segundo orden y se dibuja la trayectoria.
Referencias
Problema propuesto en la XIV Olimpiada Española de Física. Cuenca, Abril de 2003

