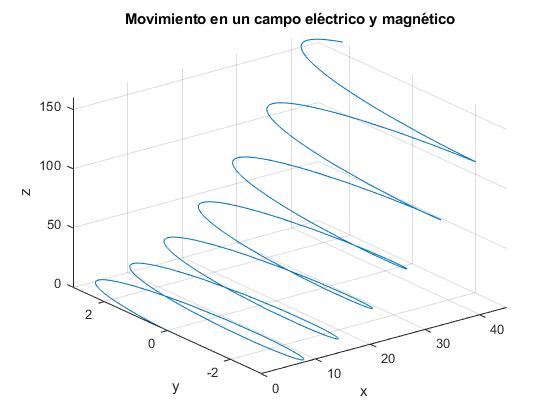
Movimiento en campos eléctrico y magnético cruzados

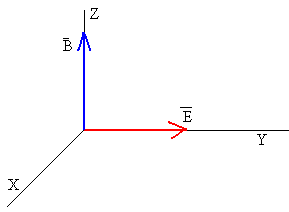
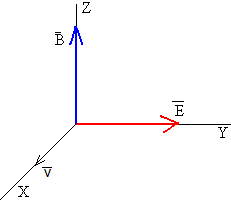
Supongamos que el campo magnético $\vec{B}$ tiene la dirección del eje Z, el campo eléctrico $\vec{E}$ la dirección del eje Y . La partícula cargada parte de la posición inicial (x₀, y₀) con velocidad inicial (v_0x, v_0y)

La fuerza que ejerce el campo eléctrico $\vec{E}$ sobre una carga q es

$\vec{f_{e}} = q \vec{E}$

La fuerza que ejerce el campo magnético $\vec{B}$ sobre una partícula de carga q cuya velocidad es $\vec{v}$ es

$\vec{f_{m}} = q \vec{v} \times \vec{B}$

La ecuación del movimiento de es

$m \frac{d^{2} \vec{r}}{d t^{2}} = q \vec{E} + q \vec{v} \times \vec{B} {\begin{cases} \vec{B} = B \hat{k} \\ \vec{E} = E \hat{j} \end{cases}$

o bien,

$m (\frac{d v_{x}}{d t} \hat{i} + \frac{d v_{y}}{d t} \hat{j} + \frac{d v_{z}}{d t} \hat{k}) = q E \hat{j} + q | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ v_{x} & v_{y} & v_{z} \\ 0 & 0 & B \end{matrix} |$

Se obtiene el siguiente sistema de ecuaciones diferenciales

$\begin{array}{l} \frac{d v_{x}}{d t} = \frac{q B}{m} v_{y} \\ \frac{d v_{y}}{d t} = \frac{q E}{m} - \frac{q B}{m} v_{x} \\ \frac{d v_{z}}{d t} = 0 \end{array}$

La velocidad a lo largo del eje Z es constante e igual a la velocidad inicial, v_z=v_0z=0

Se denomina frecuencia de giro ω al cociente ω =qB/m, que es la velocidad angular de un partícula cargada en un campo magnético uniforme.

Despejamos v_y en la primera ecuación y la introducimos en la segunda. Obtenemos la ecuación diferencial de segundo orden.

$\frac{d^{2} v_{x}}{d t^{2}} + ω^{2} v_{x} = \frac{q^{2} E B}{m^{2}}$

La solución de esta ecuación diferencial es de la forma

v_x=C·cos(ω·t)+D·sin(ω·t)+c

Introduciendo v_x en la ecuación diferencial determinamos la solución particular c de la ecuación diferencial de segundo orden.

$v_{x} = C \cos (ω \cdot t) + D \sin (ω \cdot t) + \frac{E}{B}$

Calculamos la componente v_y de la velocidad de la partícula

$v_{y} = \frac{1}{ω} \frac{d v_{x}}{d t} = - C \sin (ω \cdot t) + D cos (ω \cdot t)$

Las constantes C y D se determinan a partir de las condiciones iniciales. En el instante t=0, las componentes de la velocidad de la partícula son (v_0x, v_0y).

$\begin{array}{l} v_{x} = (v_{0 x} - \frac{E}{B}) \cos (ω \cdot t) + v_{0 y} \sin (ω \cdot t) + \frac{E}{B} \\ v_{y} = - (v_{0 x} - \frac{E}{B}) \sin (ω \cdot t) + v_{0 y} cos (ω \cdot t) \end{array}$

Para simplificar y generalizar las expresiones de las componentes de la velocidad, denominados velocidad de deriva

$v_{d} = \frac{E}{B}$

cuyo significado ya hemos visto en el selector de velocidades. Las expresiones de v_x y v_y quedarán como sigue

$\begin{array}{l} v_{x} = (v_{0 x} - v_{d}) \cos (ω \cdot t) + v_{0 y} \sin (ω \cdot t) + v_{d} \\ v_{y} = - (v_{0 x} - v_{d}) \sin (ω \cdot t) + v_{0 y} cos (ω \cdot t) \end{array}$

Sabiendo que en el instante t=0, la posición de la partícula es (x₀, y₀), calculamos la coordenada x del centro de la bola integrando la expresión de la velocidad v_x en función del tiempo, lo mismo para la ordenada y.

$\begin{array}{l} x = x_{0} + \frac{1}{ω} {(v_{0 x} - v_{d})sin(ω \cdot t) + v_{0 y} (1 - cos(ω \cdot t))} + v_{d} t \\ y = y_{0} + \frac{1}{ω} {(v_{0 x} - v_{d}) (cos(ω \cdot t) - 1) + v_{0 y} sin(ω \cdot t)} \end{array}$

Expresamos esta ecuación de la forma

$\begin{array}{l} x - x_{0} - \frac{v_{0 y}}{ω} - v_{d} t = \frac{1}{ω} {(v_{0 x} - v_{d})sin(ω \cdot t) - v_{0 y} cos(ω \cdot t)} \\ y - y_{0} + \frac{1}{ω} (v_{0 x} - v_{d}) = \frac{1}{ω} {(v_{0 x} - v_{d})cos(ω \cdot t) + v_{0 y} sin(ω \cdot t)} \end{array}$

Elevando al cuadrado y sumando

${(x - x_{0} - \frac{v_{0 y}}{ω} - v_{d} t)}^{2} + {(y - y_{0} + \frac{v_{0 x}}{ω} - \frac{v_{d}}{ω})}^{2} = \frac{1}{ω^{2}} {{(v_{0 x} - v_{d})}^{2} + v_{0 y}^{2}}$

Se trata de la ecuación de una circunferencia centrada en el punto (a, b) y tiene radio R_c

(x-a)²+(y-b)²=R_c²

donde

$\begin{array}{l} a = x_{0} + \frac{v_{0 y}}{ω} + v_{d} t b = y_{0} - \frac{v_{0 x}}{ω} + \frac{v_{d}}{ω} \\ R_{c} = \frac{1}{ω} \sqrt{{(v_{0 x} - v_{d})}^{2} + v_{0 y}^{2}} \end{array}$

El centro de la circunferencia se mueve a lo largo del eje X con velocidad v_d

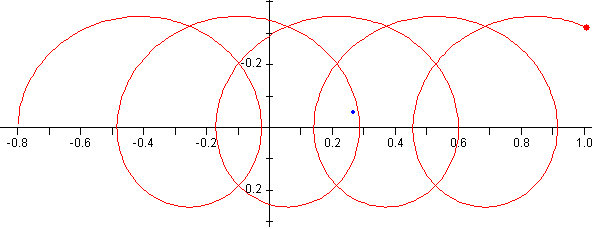
Ejemplo

Posición inicial de la partícula, x₀=0, y₀=-0.8
Velocidad inicial, v₀=0.3, φ=90º o bien, v_0x=0, v_0y=0.3
Velocidad angular, ω=qB/m=1.0
Velocidad deriva, v_d=E/B=0.05
Carga positiva

Casos particulares

Movimiento circular

Cuando el campo eléctrico es nulo, E=0, v_d=0

La partícula describe una circunferencia en el campo magnético, cuyo centro y radio son:

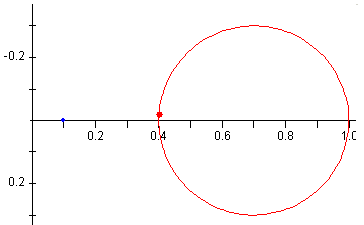
$a = x_{0} + \frac{v_{0 y}}{ω} b = y_{0} - \frac{v_{0 x}}{ω} R_{c} = \frac{v_{0}}{ω}$

Ejemplo

Posición inicial de la partícula, x₀=0, y₀=0.4
Velocidad inicial, v₀=0.3, φ=90º o bien, v_0x=0, v_0y=0.3
Velocidad angular, ω=qB/m=1.0
Velocidad deriva, v_d=E/B=0.0
Carga positiva

Movimiento rectilíneo

Si v_0y=0 y v_0x=v_d=E/B

x=x₀+v_d·t
y=y₀

La partícula se mueve a lo largo del eje X con velocidad constante igual al cociente entre la intensidad del campo eléctrico E y la intensidad del campo magnético B. Este es el fundamento de un selector de velocidades.

Ejemplo

Posición inicial de la partícula, x₀=0, y₀=0
Velocidad inicial, v₀=0.1, φ=0º o bien, v_0x=0.1, v_0y=0.0
Velocidad angular, ω=qB/m=1.0
Velocidad deriva, v_d=E/B=0.1
Carga positiva

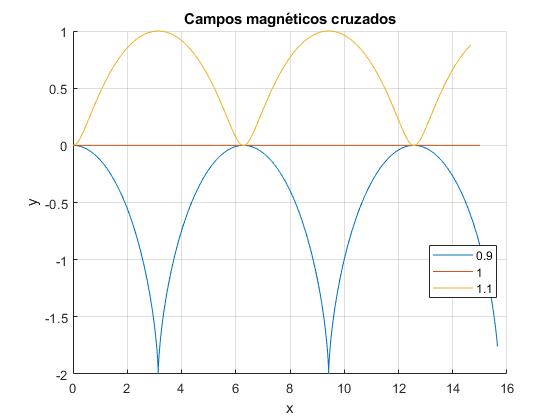
Vamos a representar las trayectorias cuando v_0x y v_d son diferentes, la trayectoria no es una línea recta. Esto es lo que le ocurriría a una partícula cargada cuando entra en un selector de velocidades y su velocidad v_0x no coincide con el cociente v_d=E/B

Representamos las trayectorias para v_0x=2v_d, v_0x=2v_d (línea recta), v_0x=0.5v_d

x0=0; %posición
y0=0;
w=1;  %qB/m
vd=1; %E/B
v0y=0;
hold on
 for v0x=[2,1,0.5]
    x=@(t) x0+((v0x-vd)*sin(w*t)+v0y*(1-cos(w*t)))/w+vd*t;
    y=@(t) y0+((v0x-vd)*(cos(w*t)-1)+v0y*sin(w*t))/w;
    fplot(x,y, [0,15]);
 end
hold off
grid on
legend('0.9','1','1.1','location','best')
xlabel('x')
ylabel('y')
title('Campos magnéticos cruzados')

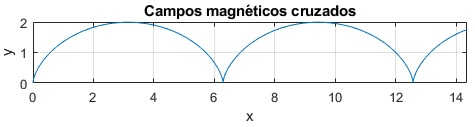
Cuando la partícula parte del reposo

v_0x=v_0y=0 desde el origen x₀=0, y₀=0

$x = \frac{v_{d}}{ω} (ω \cdot t -sin (ω \cdot t)) y = \frac{v_{d}}{ω} (1 - cos(ω ·t))$

Estas son las ecuaciones paramétricas de una cicloide generada por un punto del borde de un disco de radio R=v_d/ω=E/(ωB) que rueda sin deslizar, girando alrededor de su eje con velocidad angular ω y cuyo centro se mueve con velocidad constante v=R·ω=E/B.

Ejemplo

Posición inicial de la partícula, x₀=0, y₀=0
Velocidad inicial, v_0x=v_0y=0
Velocidad angular, ω=qB/m=1.0
Velocidad deriva, v_d=E/B=1.0
Carga positiva

w=1; %qB/m
vd=1; %E/B
v0x=0; %velocidad inicial
v0y=0; 
x0=0;%posición inicial
y0=0;
x=@(t) x0+vd*t+((v0x-vd)*sin(w*t)+v0y*(1-cos(w*t)))/w;
y=@(t) y0+(v0y*sin(w*t)-(v0x-vd)*(1-cos(w*t)))/w;
fplot(x,y,[0,15])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Campos magnéticos cruzados')

La velocidad de deriva v_d no depende de la carga de las partículas, por lo que los electrones derivan en la misma dirección que los iones positivos. Pero el movimiento de giro ω de los electrones es opuesto al de las cargas positivas.

Cuando v_0x=v_d

$\begin{array}{l} x = \frac{v_{0 y}}{ω} (1 - \cos (ω \cdot t)) + v_{d} t \\ y = \frac{v_{0 y}}{ω} \sin (ω \cdot t) \end{array}$

Ejemplo

Posición inicial de la partícula, x₀=0, y₀=0
Velocidad angular, ω=qB/m=1.0
Velocidad deriva, v_d=E/B=1
Velocidad inicial, v_0y=0.3, 1 y 3
Carga positiva

x0=0; %posición
y0=0;
w=1;  %qB/m
vd=1; %E/B
v0x=vd;
hold on
for v0y=[0.3,1,3]
    x=@(t) x0+((v0x-vd)*sin(w*t)+v0y*(1-cos(w*t)))/w+vd*t;
    y=@(t) y0+((v0x-vd)*(cos(w*t)-1)+v0y*sin(w*t))/w;
    fplot(x,y, [0,20]);
end
hold off
grid on
legend('0.3','1','3','location','southwest')
xlabel('x')
ylabel('y')
title('Campos magnéticos cruzados')

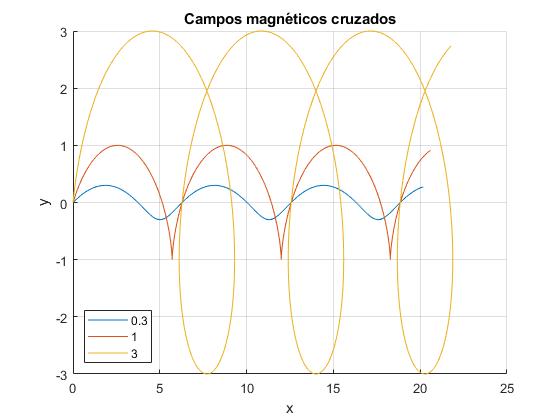
El lector puede explorar otras posibilidades

Actividades

Se introduce

La posición de partida x₀, en el control titulado Posición inicial. La ordenada se ha fijado en y₀=0.
La velocidad angular de giro ω=qB/m, en el control titulado Velocidad angular
La velocidad inicial v₀ de la partícula en el control titulado Velocidad inicial
La dirección φ del vector velocidad inicial v₀, en el control titulado Dirección velocidad. Las componentes del vector velocidad son: v_0x=v₀·cosφ, v_0y=v₀·sinφ.
La velocidad de deriva v_d=E/B en el control titulado Velocidad deriva
La carga positiva o negativa, activando el botón de radio correspondiente

Se pulsa el botón titulado Nuevo

Se observa el movimiento de la partícula cargada en el campo electromagnético.

Ejemplo 1

Intensidad del campo magnético, B=500 gauss=0.05 T
Intensidad del campo eléctrico, E=20000 N/C
Partícula: protón, carga positiva, q=1.6·10^-19 C, m=1.67·10^-27 kg

La velocidad angular ω y la velocidad de deriva v_d valen, respectivamente,

$ω = \frac{q B}{m} = 4.79 \cdot 10^{6} rad/s v_{d} = \frac{E}{B} = 0.4 \cdot 10^{6} m/s$

Suponiendo que el tiempo se mide en μs=10^-6 s, introducimos en el control titulado Velocidad angular 4.79 y en el control titulado Velocidad deriva, 0.4. Probar con distintas velocidades iniciales, por ejemplo, v₀=0.5, y orientaciones del vector velocidad inicial.

Ejemplo 2

Intensidad del campo magnético, B=0.5 gauss=0.5·10^-4 T
Intensidad del campo eléctrico, E=20 N/C
Partícula: electrón, carga negativa, q=1.6·10^-19 C, m=9.1·10^-31 kg

La velocidad angular ω, y la velocidad de deriva v_d valen, respectivamente,

$ω = \frac{q B}{m} = 8.791 \cdot 10^{6} rad/s v_{d} = \frac{E}{B} = 0.4 \cdot 10^{6} m/s$

Suponiendo que el tiempo se mide en μs=10^-6 s, introducimos en el control titulado Velocidad angular 8.791 y en el control titulado Velocidad deriva, 0.4. Probar con distintas velocidades iniciales, por ejemplo v₀=0.5 m/s y con distintas orientaciones del vector velocidad inicial.

Posición inicial:
Velocidad inicial: Dirección velocidad:
Velocidad angular qB/m: Velocidad deriva:

Movimiento en un campo electromagnético

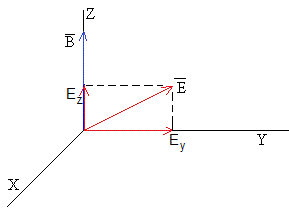
Las direcciones del campo magnético $\vec{B}$ y del campo eléctrico $\vec{E}$ están contenidas en el plano ZY. La dirección del campo magnético es el eje Z, tal como se muestra en la figura. La partícula cargada parte del origen con velocidad inicial (v_0x, v_0y, v_0z)

La ecuación del movimiento de la partícula cargada es

$\begin{array}{l} m \frac{d^{2} \vec{r}}{d t^{2}} = q \vec{E} + q \vec{v} \times \vec{B} {\begin{cases} \vec{B} = B \hat{k} \\ \vec{E} = E_{y} \hat{j} + E_{z} \hat{k} \end{cases} \\ m (\frac{d v_{x}}{d t} \hat{i} + \frac{d v_{y}}{d t} \hat{j} + \frac{d v_{z}}{d t} \hat{k}) = q (E_{y} \hat{j} + E_{z} \hat{k}) + q | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ v_{x} & v_{y} & v_{z} \\ 0 & 0 & B \end{matrix} | \end{array}$

El resultado es el sistema de tres ecuaciones diferenciales

${\begin{cases} \frac{d v_{x}}{d t} = ω v_{y} \\ \frac{d v_{y}}{d t} = \frac{q E_{y}}{m} - ω v_{x} \\ \frac{d v_{z}}{d t} = \frac{q E_{z}}{m} \end{cases}$

La última ecuación corresponde a un movimiento uniformemente acelerado

$\begin{array}{l} v_{z} = \frac{q E_{z}}{m} t + v_{0 z} \\ z = \frac{1}{2} \frac{q E_{z}}{m} t^{2} + v_{0 z} t \end{array}$

Las dos primeras ecuaciones diferenciales se resuelven de forma similar al apartado anterior. Derivamos la segunda ecuación respecto del tiempo

$\begin{array}{l} \frac{d^{2} v_{y}}{d t^{2}} = - ω \frac{d v_{x}}{d t} \\ \frac{d^{2} v_{y}}{d t^{2}} + ω^{2} v_{y} = 0 \end{array}$

La solución de esta ecuación diferencial es conocida

$v_{y} = C \cos (ω t) + D \sin (ω t)$

Donde C y D se determinan a partir de la velocidad inicial. En el instante t=0, v_0y=C. De la ecuación

$\begin{array}{l} \frac{d v_{y}}{d t} = \frac{q E_{y}}{m} - ω v_{x} \\ ω (- C \sin (ω t) + D \cos (ω t)) = \frac{q E_{y}}{m} - ω v_{x} \\ v_{x} = \frac{E_{y}}{B} + C \sin (ω t) - D \cos (ω t) \end{array}$

En el instante inicial t=0, v_x=v_0x

$D = \frac{q E_{y}}{ω m} - v_{0 x}$

Las componentes de la velocidad v_x y v_y en función del tiempo son

$\begin{array}{l} v_{y} = v_{0 y} \cos (ω t) + (\frac{E_{y}}{B} - v_{0 x}) \sin (ω t) \\ v_{x} = \frac{E_{y}}{B} + v_{0 y} \sin (ω t) - (\frac{E_{y}}{B} - v_{0 x}) \cos (ω t) \end{array}$

Integrando, obtenemos las coordenadas x, y y z en función del tiempo t, sabiendo que la partícula parte del origen

$\begin{array}{l} x = \frac{E_{y}}{B} t + \frac{1}{ω} {(v_{0 x} - \frac{E_{y}}{B}) \sin (ω t) + v_{0 y} (1 - \cos (ω t))} \\ y = \frac{1}{ω} {v_{0 y} \sin (ω t) - (v_{0 x} - \frac{E_{y}}{B}) (1 - \cos (ω t))} \\ z = \frac{1}{2} ω \frac{E_{z}}{B} t^{2} + v_{0 z} t \end{array}$

Si E_z=0, los campos eléctrico y magnético son perpendiculares, tenemos las mismas ecuaciones del apartado anterior
Cuando el campo eléctrico es nulo y la velocidad inicial de la partícula a lo largo del eje Z no es nula, tenemos una trayectoria helicoidal

Ejemplo 1

Los campos eléctrico y magnético son paralelos al eje Z, E_y=0

Las dos primeras ecuaciones de la trayectoria se escriben

${\begin{cases} x - \frac{v_{0 y}}{ω} = \frac{v_{0 x}}{ω} \sin (ω t) - \frac{v_{0 y}}{ω} \cos (ω t) \\ y + \frac{v_{0 x}}{ω} = \frac{v_{0 y}}{ω} \sin (ω t) + \frac{v_{0 x}}{ω} \cos (ω t) \end{cases}$

Elevando al cuadrado y sumando, obtenemos en el plano XY, la ecuación de una circunferencia centrada en (v_0x/ω, -v_0y/ω)

$\begin{array}{l} {(x - \frac{v_{0 y}}{ω})}^{2} + {(y + \frac{v_{0 x}}{ω})}^{2} = \frac{1}{ω^{2}} (v_{0 x}^{2} + v_{0 y}^{2}) \\ z = \frac{1}{2} ω \frac{E_{z}}{B} t^{2} + v_{0 z} t \end{array}$

El resultado es una hélice de paso constante si E_z=0, y v_0z≠0. Si E_z≠0, el paso es variable

w=1; %qB/m
vd_y=0; %E_y/B
vd_z=0.2; %E_z/B
v0x=0.3; %velocidad inicial
v0y=0; 
v0z=0;
%trayectoria
x=@(t) vd_y*t+((v0x-vd_y)*sin(w*t)+v0y*(1-cos(w*t)))/w;
y=@(t) (v0y*sin(w*t)-(v0x-vd_y)*(1-cos(w*t)))/w;
z=@(t) vd_z*w*t.^2/2+v0z*t;
fplot3(x,y,z,[0,20])
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en un campo eléctrico y magnético')

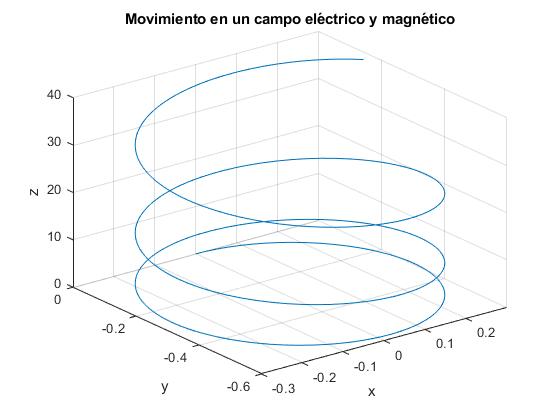
Ejemplo 2

Si v_0x=E_y/ω y v_0y=0

$\begin{array}{l} x = \frac{E_{y}}{B} t \\ y = 0 \\ z = \frac{1}{2} ω \frac{E_{z}}{B} t^{2} + v_{0 z} t \end{array}$

La trayectoria es una parábola en el plano XZ

$z = \frac{1}{2} ω \frac{E_{z} B}{E_{y}^{2}} x^{2} + v_{0 z} \frac{B}{E_{y}} x$

w=1; %qB/m
vd_y=1; %E_y/B
vd_z=0.2; %E_z/B
v0x=vd_y; %velocidad inicial
v0y=0; 
v0z=0;
%trayectoria
x=@(t) vd_y*t+((v0x-vd_y)*sin(w*t)+v0y*(1-cos(w*t)))/w;
y=@(t) (v0y*sin(w*t)-(v0x-vd_y)*(1-cos(w*t)))/w;
z=@(t) vd_z*w*t.^2/2+v0z*t;
fplot3(x,y,z,[0,20])
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en un campo eléctrico y magnético')

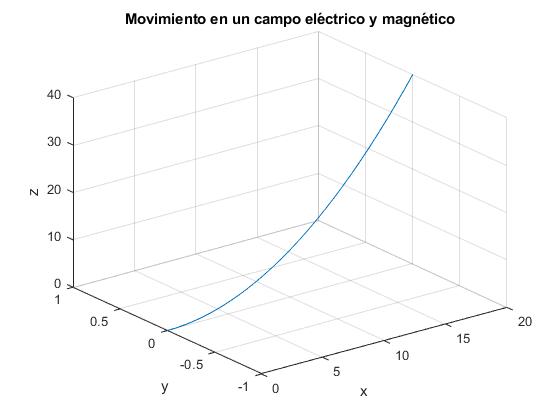
Ejemplo 3

Si v_0x=0 y v_0y=0.

$\begin{array}{l} x = \frac{1}{ω} \frac{E_{y}}{B} (ω t - \sin (ω t)) \\ y = \frac{1}{ω} \frac{E_{y}}{B} (1 - \cos (ω t)) \\ z = \frac{1}{2} ω \frac{E_{z}}{B} t^{2} + v_{0 z} t \end{array}$

Tenemos una cicloide en el plano XY

w=1; %qB/m
vd_y=1; %E_y/B
vd_z=0.2; %E_z/B
v0x=0; %velocidad inicial
v0y=0; 
v0z=0;
%trayectoria
x=@(t) vd_y*t+((v0x-vd_y)*sin(w*t)+v0y*(1-cos(w*t)))/w;
y=@(t) (v0y*sin(w*t)-(v0x-vd_y)*(1-cos(w*t)))/w;
z=@(t) vd_z*w*t.^2/2+v0z*t;
fplot3(x,y,z,[0,20])
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en un campo eléctrico y magnético')

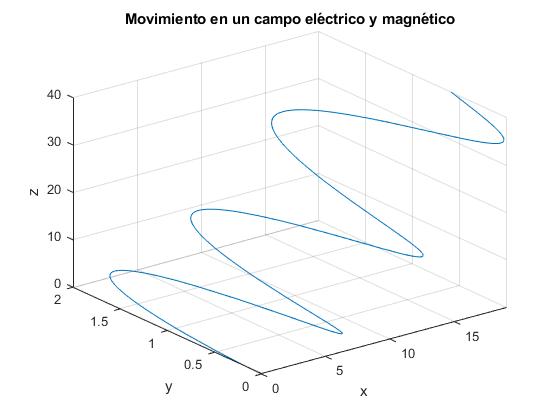
Otras trayectorias más complejas, se obtienen modificando las velocidades iniciales v_0x y v_0y

w=1; %qB/m
vd_y=1; %E_y/B
vd_z=0.2; %E_z/B
v0x=vd_y; %velocidad inicial
v0y=3; 
v0z=0;
%trayectoria
x=@(t) vd_y*t+((v0x-vd_y)*sin(w*t)+v0y*(1-cos(w*t)))/w;
y=@(t) (v0y*sin(w*t)-(v0x-vd_y)*(1-cos(w*t)))/w;
z=@(t) vd_z*w*t.^2/2+v0z*t;
fplot3(x,y,z,[0,40])
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento en un campo eléctrico y magnético')

Casos particulares

Movimiento circular

Movimiento rectilíneo

Cuando la partícula parte del reposo

Cuando v0x=vd

Actividades

Movimiento en un campo electromagnético

Cuando v_0x=v_d