El espectrómetro de masas sin tener en cuenta el peso del ión.

Consideremos un ión de carga +q y masa m que sale del origen con velocidad v₀ en la dirección del eje Z tal como se muestra en la figura. El ión se mueve en una región del plano YZ donde hay un campo magnético uniforme B cuya dirección es el eje X.

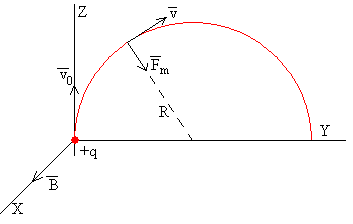
La fuerza que ejerce el campo magnético sobre la partícula cargada es

${\displaystyle \overrightarrow{f_m}=q\overrightarrow{v}\times \overrightarrow{B}}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{d^2\overrightarrow{r}}{d{t}^2}=q(v_y\widehat{j}+v_z\widehat{k})\times B\widehat{i}\hfill \\ m\frac{d^2\overrightarrow{r}}{d{t}^2}=qB(v_z\widehat{j}-v_y\widehat{k})\hfill \end{array}}$

o bien,

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{t}^2}=\omega \frac{dz}{dt}\omega =\frac{qB}{m}\\ \frac{d^{2}z}{d{t}^2}=-\omega \frac{dy}{dt}\end{array}}$

Tenemos que resolver este sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales: en el instante t=0, el ión parte del origen con velocidad v_z=v₀

Integramos la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{dy}{dt}-\omega z\right)=0\\ \frac{dy}{dt}-\omega z=c_1\end{array}}$

Determinamos la constante de integración c₁ a partir de las condiciones iniciales: en el origen z=0, v_y=dy/dt=0, resultando c₁=0.

${\displaystyle \frac{dy}{dt}-\omega z=0}$

Integramos la segunda ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{dz}{dt}+\omega y\right)=0\\ \frac{dz}{dt}+\omega y=c_2\end{array}}$

Determinamos la constante de integración c₂ a partir de las condiciones iniciales: en el origen y=0, v_z=dz/dt=v₀, resultando c₂=v₀.

${\displaystyle \frac{dz}{dt}+\omega y=v_0}$

Hemos reducido un sistema de dos ecuaciones diferenciales de segundo orden a un sistema de dos ecuaciones diferenciales de primer orden

${\displaystyle \begin{array}{l}\frac{dy}{dt}-\omega z=0\\ \frac{dz}{dt}+\omega y=v_0\end{array}}$

Derivamos la segunda ecuación respecto de z e introducimos la expresión dy/dt de la primera

${\displaystyle \frac{d^{2}z}{d{t}^2}+{\omega }^{2}z=0}$

Esta es la ecuación diferencial de un Movimiento Armónico Simple, la solución es z=Asin(ωt)+Bcos (ωt). Los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, z=0, dz/dt=v₀. Resultando B=0, y A=v₀/ω

${\displaystyle z=\frac{v_0}{\omega }\sin \left(\omega t\right)}$

Derivamos respecto de z y despejamos y en la segunda ecuación diferencial

${\displaystyle y=\frac{v_0}{\omega }-\frac{v_0}{\omega }\cos \left(\omega t\right)}$

Estas son las ecuaciones paramétricas de la trayectoria, eliminando el tiempo t entre ambas ecuaciones.

${\displaystyle z^2+{\left(y-\frac{v_0}{\omega }\right)}^2={\left(\frac{v_0}{\omega }\right)}^2}$

que es la ecuación de una circunferencia centrada en (y, z)=(v₀/ω, 0) y de radio

${\displaystyle R=\frac{v_0}{\omega }=\frac{m{v}_0}{qB}}$

que es el resultado que ya obtuvimos en la página anterior.

El espectrómetro de masas teniendo en cuenta el peso del ión.

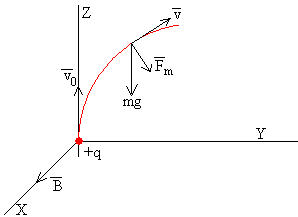
La ecuación del movimiento de la partícula es ahora

${\displaystyle \begin{array}{l}m\frac{d^2\overrightarrow{r}}{d{t}^2}=q(v_y\widehat{j}+v_z\widehat{k})\times B\widehat{i}-mg\widehat{k}\hfill \\ m\frac{d^2\overrightarrow{r}}{d{t}^2}=qB(v_z\widehat{j}-v_y\widehat{k})-mg\widehat{k}\hfill \end{array}}$

o bien,

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{t}^2}=\omega \frac{dz}{dt}\omega =\frac{qB}{m}\\ \frac{d^{2}z}{d{t}^2}=-\omega \frac{dy}{dt}-g\end{array}}$

Tenemos que resolver este sistema de ecuaciones diferenciales con las siguientes condiciones iniciales: en el instante t=0, el ión parte del origen con velocidad v_z=v₀

Integramos la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{dy}{dt}-\omega z\right)=0\\ \frac{dy}{dt}-\omega z=c_1\end{array}}$

Determinamos la constante de integración c₁ a partir de las condiciones iniciales: en el origen z=0, v_y=dy/dt=0, resultando c₁=0.

Integramos la segunda ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{dz}{dt}+\omega y\right)=-g\\ \frac{dz}{dt}+\omega y=-gt+c_2\end{array}}$

Determinamos la constante de integración c₂ a partir de las condiciones iniciales: en el instante t=0, y=0, v_z=dz/dt=v₀,  resultando c₂=v₀.

${\displaystyle \frac{dz}{dt}+\omega y=-gt+v_0}$

Hemos reducido un sistema de dos ecuaciones diferenciales de segundo orden a un sistema de dos ecuaciones diferenciales de primer orden

${\displaystyle \begin{array}{l}\frac{dy}{dt}-\omega z=0\\ \frac{dz}{dt}+\omega y=-gt+v_0\end{array}}$

Derivamos la segunda ecuación respecto de z y sustituimos la expresión de dy/dt de la primera ecuación.

${\displaystyle \frac{d^{2}z}{d{t}^2}+{\omega }^{2}z=-g}$

La solución particular de esta ecuación diferencial es z₁=c₃. Introduciéndola en la ecuación diferencial obtenemos z₁=c₃=-g/ω².

La solución de la ecuación diferencial homogénea es z₂=Asin(ωt)+Bcos (ωt).

La solución completa es z=z₁+z₂

${\displaystyle z=A\sin \left(\omega t\right)+B\cos \left(\omega t\right)-\frac{g}{{\omega }^2}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, z=0, v_z=dz/dt=v₀. Resultando B= g/ω², y A=v₀/ω

${\displaystyle z=\frac{v_0}{\omega }\sin \left(\omega t\right)+\frac{g}{{\omega }^2}\cos \left(\omega t\right)-\frac{g}{{\omega }^2}}$

Derivamos respecto de z y despejamos y en la segunda ecuación diferencial

${\displaystyle y=\frac{g}{{\omega }^2}\sin \left(\omega t\right)-\frac{v_0}{\omega }\cos \left(\omega t\right)+\frac{v_0}{\omega }-\frac{g}{{\omega }^2}(\omega t)}$

En un espectrómetro real g<<ω², la trayectoria de un ión es una semicircunfencia, tal como se ha descrito en el apartado anterior.

Intersección del haz de iones con el eje Y

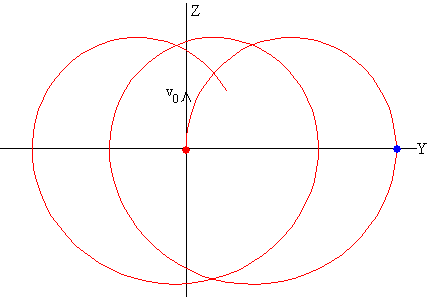
En la primera ecuación paramétrica ponemos z=0, y calculamos las raíces de la ecuación

${\displaystyle \begin{array}{l}\frac{v_0}{\omega }\sin \left(\omega t\right)+\frac{g}{{\omega }^2}\cos \left(\omega t\right)=\frac{g}{{\omega }^2}\\ A\sin \left(\omega t+\phi \right)=\frac{g}{{\omega }^2}\\ A\cos \phi =\frac{v_0}{\omega }A\sin \phi =\frac{g}{{\omega }^2}\phi =\arctan \frac{g}{\omega v_0}\end{array}}$

La ecuación se escribe

Asin(ωt+φ)=Asin(φ)

o bien,

sin(ωt+φ)=sin(φ)

Una solución es ωt=2nπ, n=0, 1, 2, 3…

La solución n=0 corresponde a t=0, cuando el ión sale del origen

La otra solución es

ωt=(2n+1)π-2φ.

Cuando n=0, tenemos ωt=π-2φ que corresponde a la primera intersección del haz de iones con el eje Y, tal como se señala en la figura mediante un círculo de color azul.

La coordenada y del primer punto de impacto es

$$\begin{gathered} {\displaystyle y=A\sin \phi \sin (\omega t)-A\cos \phi \cos (\omega t)+\frac{v_0}{\omega }-\frac{g}{{\omega }^2}(\omega t)= \\ -A\cos (\omega t+\phi )+\frac{v_0}{\omega }-\frac{g}{{\omega }^2}(\omega t)} \end{gathered}$$

En el instante t tal que ωt=π-2φ

${\displaystyle y_1=-A\cos (\pi -\phi )+\frac{v_0}{\omega }-\frac{g}{{\omega }^2}(\pi -2\phi )=2\frac{v_0}{\omega }-\frac{g}{{\omega }^2}\left(\pi -2\arctan \frac{g}{v_0\omega }\right)}$

Ecuaciones paramétricas de la trayectoria

Escribimos las ecuaciones paramétricas de la trayectoria en términos de dos parámetros

${\displaystyle \begin{array}{l}\alpha =\frac{g}{{\omega }^2}\beta =\frac{v_0}{\omega }\\ z=\beta \sin \left(\omega t\right)+\alpha \cos \left(\omega t\right)-\alpha \\ y=\alpha \sin \left(\omega t\right)-\beta \cos \left(\omega t\right)+\beta -\alpha (\omega t)\end{array}}$

Vamos dando valores a ωt para dibujar la trayectoria.

wt=linspace(0,20,200);
alfa=0.1;
beta=1;
z=beta*sin(wt)+alfa*cos(wt)-alfa;
y=alfa*sin(wt)-beta*cos(wt)+beta-alfa*wt;
plot(y,z)
axis equal
grid on
xlabel('y')
ylabel('z')
title('Espectrómetro de masas')

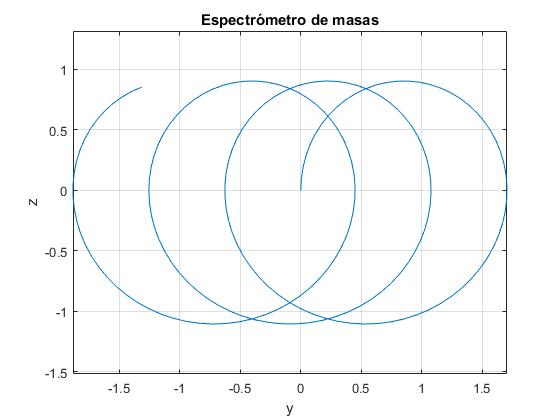
Los puntos de intersección con el eje Y, es decir, z=0 se calculan del siguiente modo

${\displaystyle \begin{array}{l}\omega t=\pi -2\arctan \frac{\alpha }{\beta }{y}_1=2\beta -\alpha \left(\pi -2\arctan \frac{\alpha }{\beta }\right)\\ \omega t=2\pi y_2=-2\pi \alpha \\ \omega t=3\pi -2\arctan \frac{\alpha }{\beta }{y}_3=2\beta -\alpha \left(3\pi -2\arctan \frac{\alpha }{\beta }\right)\\ \omega t=4\pi y_4=-4\pi \alpha \end{array}}$

y así, sucesivamente

Si no se tuvieran en cuenta el peso de los iones g=0, α=0 e y_2n+1=2β, y_2n=0, con n=0.1,2,3…

Actividades

Se introduce

• El parámetro α, en el control titulado alfa
• El parámetro β, en el control titulado beta

Se pulsa el botón titulado Nuevo. Utilice los botones pausa || y paso a paso >| para acercarse a la intersección de la trayectoria del ión con el eje Y

Se observa el movimiento del ión “pesado”

Se mide las intersecciones con el eje Y, es decir, cuando z=0, y se comprueban con las calculadas.

Ejemplo.

Sea α=0.1 y β=1.0

Referencias

Gondar J. L., Costa B. The mass spectrograph revisited. Eur. J. Phys. 20 (1999) 469-475