El campo magnético producido por un monopolo de carga q_m es similar al campo eléctrico producido por una carga puntual

${\displaystyle \overrightarrow{B}=\frac{{\mu }_0}{4\pi }\frac{q_m}{r^2}\widehat{r}}$

Una partícula de masa m que lleva una carga eléctrica q en el seno de dicho campo magnético experimenta una fuerza, $\overrightarrow{F}=q(\overrightarrow{v}\times \overrightarrow{B})$. La ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{d^2\overrightarrow{r}}{d{t}^2}=q\left(\overrightarrow{v}\times \frac{{\mu }_0}{4\pi }\frac{q_m}{r^2}\widehat{r}\right)\\ \frac{d^2\overrightarrow{r}}{d{t}^2}=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\left(\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{r}\right)\end{array}}$

Constantes del movimiento

• La energía cinética de la partícula cargada es constante

Multiplicamos escalarmente por el vector velocidad $\frac{d\overrightarrow{r}}{dt}$

${\displaystyle \begin{array}{l}\frac{d\overrightarrow{r}}{dt}·\frac{d^2\overrightarrow{r}}{d{t}^2}=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\frac{d\overrightarrow{r}}{dt}·\left(\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{r}\right)=0\\ \frac{d\overrightarrow{r}}{dt}·\frac{d^2\overrightarrow{r}}{d{t}^2}=\frac{1}{2}\frac{d}{dt}\left(\frac{d\overrightarrow{r}}{dt}·\frac{d\overrightarrow{r}}{dt}\right)=0\\ \frac{d}{dt}\left(\frac{1}{2}{v}^2\right)=0\\ v^2=\text{cte}\end{array}}$

• El momento angular $\overrightarrow{L}$ no es constante, pero lo es, el cuadrado de su módulo L²

${\displaystyle \begin{array}{l}\overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}=\overrightarrow{r}\times m\frac{d\overrightarrow{r}}{dt}\\ \frac{d}{dt}\left(\overrightarrow{L}·\overrightarrow{L}\right)=2\overrightarrow{L}\frac{d\overrightarrow{L}}{dt}=2\overrightarrow{L}\left(\frac{d\overrightarrow{r}}{dt}\times m\frac{d\overrightarrow{r}}{dt}+\overrightarrow{r}\times m\frac{d^2\overrightarrow{r}}{d{t}^2}\right)=2\overrightarrow{L}\left(\overrightarrow{r}\times m\frac{d^2\overrightarrow{r}}{d{t}^2}\right)=\\ 2\overrightarrow{L}\left(\overrightarrow{r}\times \frac{{\mu }_0}{4\pi }\frac{q{q}_m}{r^3}\left(\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{r}\right)\right)=-2\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\overrightarrow{L}\left(\overrightarrow{r}\times \left(\overrightarrow{r}\times m\frac{d\overrightarrow{r}}{dt}\right)\right)=-2\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\overrightarrow{L}\left(\overrightarrow{r}\times \overrightarrow{L}\right)=0\end{array}}$

• La magnitud $\overrightarrow{J}$ es constante del movimiento

Efectuamos

${\displaystyle \overrightarrow{r}\times \frac{d^2\overrightarrow{r}}{d{t}^2}=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\overrightarrow{r}\times \left(\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{r}\right)}$

El miembro izquierdo se convierte en

${\displaystyle \frac{d}{dt}\left(\overrightarrow{r}\times \frac{d\overrightarrow{r}}{dt}\right)=\frac{d\overrightarrow{r}}{dt}\times \frac{d\overrightarrow{r}}{dt}+\overrightarrow{r}\times \frac{d^2\overrightarrow{r}}{d{t}^2}=\overrightarrow{r}\times \frac{d^2\overrightarrow{r}}{d{t}^2}}$

Teniendo en cuenta el resultado del triple producto vectorial

${\displaystyle \overrightarrow{A}\times \left(\overrightarrow{B}\times \overrightarrow{C}\right)=\overrightarrow{B}\left(\overrightarrow{A}·\overrightarrow{C}\right)-\overrightarrow{C}\left(\overrightarrow{A}·\overrightarrow{B}\right)}$

El miembro derecho

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\overrightarrow{r}\times \frac{d\overrightarrow{r}}{dt}\right)=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\overrightarrow{r}\times \left(\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{r}\right)=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\left\{\frac{d\overrightarrow{r}}{dt}\left(\overrightarrow{r}·\overrightarrow{r}\right)-\overrightarrow{r}\left(\overrightarrow{r}·\frac{d\overrightarrow{r}}{dt}\right)\right\}=\\ \frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\left\{r^2\frac{d\overrightarrow{r}}{dt}-\overrightarrow{r}\left(\frac{1}{2}\frac{d\left(\overrightarrow{r}·\overrightarrow{r}\right)}{dt}\right)\right\}=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\left\{r^2\frac{d\overrightarrow{r}}{dt}-\overrightarrow{r}\left(\frac{1}{2}\frac{d{r}^2}{dt}\right)\right\}=\\ \frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\left\{r^2\frac{d\overrightarrow{r}}{dt}-\overrightarrow{r}\left(r\frac{dr}{dt}\right)\right\}=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^2}\left\{r\frac{d\overrightarrow{r}}{dt}-\overrightarrow{r}\frac{dr}{dt}\right\}=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{d}{dt}\left(\frac{\overrightarrow{r}}{r}\right)\end{array}}$

La derivada respecto del tiempo de la magnitud $\overrightarrow{J}$ es nula. Tenemos otra constante del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\overrightarrow{r}\times \frac{d\overrightarrow{r}}{dt}-\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{\overrightarrow{r}}{r}\right)=0\\ \frac{d}{dt}\left(\overrightarrow{r}\times m\frac{d\overrightarrow{r}}{dt}-\frac{{\mu }_{0}q{q}_m}{4\pi }\frac{\overrightarrow{r}}{r}\right)=0\\ \overrightarrow{J}=\overrightarrow{L}-\frac{{\mu }_{0}q{q}_m}{4\pi }\frac{\overrightarrow{r}}{r}\end{array}}$



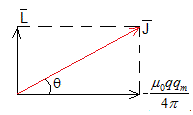
El vector $\overrightarrow{J}$ es la suma de dos vectores mutuamente perpendiculares

${\displaystyle \frac{{\mu }_{0}q{q}_m}{4\pi }\frac{\overrightarrow{r}}{r}·\overrightarrow{L}=\frac{{\mu }_{0}q{q}_m}{4\pi }\frac{\overrightarrow{r}}{r}·\left(\overrightarrow{r}\times m\frac{d\overrightarrow{r}}{dt}\right)=0}$

Su módulo es

${\displaystyle J=\sqrt{L^2+{\left(\frac{{\mu }_{0}q{q}_m}{4\pi }\right)}^2}}$

Calculamos el producto escalar $\widehat{r}·\overrightarrow{J}$, o el ángulo θ

${\displaystyle \begin{array}{l}\overrightarrow{J}=\overrightarrow{r}\times m\frac{d\overrightarrow{r}}{dt}-\frac{{\mu }_{0}q{q}_m}{4\pi }\frac{\overrightarrow{r}}{r}\\ \widehat{r}·\overrightarrow{J}=-\frac{{\mu }_{0}q{q}_m}{4\pi }\\ \cos \theta =\frac{\widehat{r}·\overrightarrow{J}}{J}=\frac{-\frac{{\mu }_{0}q{q}_m}{4\pi }}{J},\sin \theta =\frac{L}{J}\end{array}}$

El producto escalar $\widehat{r}·\overrightarrow{J}$ es constante, lo que implica que la partícula cargada cuyo vector posición es $\overrightarrow{r}$ forma un ángulo constante con el vector $\overrightarrow{J}$, se mueve en la superficie de un cono que forma un ángulo fijo.

Trayectoria

El hecho de que la energía cinética sea una constante del movimiento, nos permite obtener información acerca del movimiento en la dirección radial de la partícula

Multiplicamos la ecuación del movimiento escalarmente por el vector $\overrightarrow{r}$

${\displaystyle \overrightarrow{r}\frac{d^2\overrightarrow{r}}{d{t}^2}=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\overrightarrow{r}·\left(\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{r}\right)=0}$

La aceleración es perpendicular al vector $\overrightarrow{r}$, es decir, a la superficie del cono. La distancia r de la partícula cargada al monopolo r es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\overrightarrow{r}·\frac{d\overrightarrow{r}}{dt}\right)=\frac{d\overrightarrow{r}}{dt}·\frac{d\overrightarrow{r}}{dt}+\overrightarrow{r}\frac{d^2\overrightarrow{r}}{d{t}^2}=v^2+0=v^2\\ \overrightarrow{r}·\frac{d\overrightarrow{r}}{dt}=v^{2}t+C_1\\ \frac{1}{2}\frac{d}{dt}\left(\overrightarrow{r}·\overrightarrow{r}\right)·=v^{2}t+C_1\\ r^2=2v^2\frac{t^2}{2}+2C_{1}t+C_2\end{array}}$

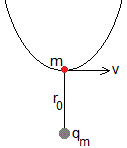
C₁ y C₂ son constantes de integración que se determinan a partir de las condiciones iniciales. Se elige C₁=0, y $C_2=r_0^2$, siendo r₀ la distancia más cercana de la partícula cargada al monopolo

${\displaystyle r^2=v^2{t}^2+r_0^2}$

El módulo del momento angular, L=mvr₀

Coordenadas esféricas

Para completar la ecuación de la trayectoria es conveniente formular las ecuaciones del movimiento en coordenadas esféricas

• El vector posición

${\displaystyle \overrightarrow{r}=r\widehat{r}}$

• El vector velocidad

${\displaystyle \frac{d\overrightarrow{r}}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }+r\sin \theta \frac{d\phi }{dt}\widehat{\phi }}$

• El vector aceleración

${\displaystyle \begin{array}{l}\frac{d^2\overrightarrow{r}}{d{t}^2}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2-r{\left(\frac{d\phi }{dt}\right)}^2{\sin }^2\theta \right)\widehat{r}+\\ \left(2\frac{dr}{dt}\frac{d\theta }{dt}+r\frac{d^2\theta }{d{t}^2}-r{\left(\frac{d\phi }{dt}\right)}^2\sin \theta ·\cos \theta \right)\widehat{\theta }\\ +\left(2\frac{dr}{dt}\frac{d\phi }{dt}\sin \theta +2r\frac{d\phi }{dt}\frac{d\theta }{dt}\cos \theta +r\frac{d^2\phi }{d{t}^2}\sin \theta \right)\widehat{\phi }\end{array}}$

Teniendo en cuenta que el ángulo θ es constante. La ecuación del movimiento en coordenadas esféricas es

${\displaystyle \begin{array}{l}\frac{d^2\overrightarrow{r}}{d{t}^2}=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\left(\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{r}\right)\\ \left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\phi }{dt}\right)}^2{\sin }^2\theta \right)\widehat{r}+\left(-r{\left(\frac{d\phi }{dt}\right)}^2\sin \theta ·\cos \theta \right)\widehat{\theta }+\left(2\frac{dr}{dt}\frac{d\phi }{dt}\sin \theta +r\frac{d^2\phi }{d{t}^2}\sin \theta \right)\widehat{\phi }=\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}\left|\begin{array}{ccc}\widehat{r}& \widehat{\theta }& \widehat{\phi }\\ \frac{dr}{dt}& 0& r\sin \theta \frac{d\phi }{dt}\\ r& 0& 0\end{array}\right|\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\phi }{dt}\right)}^2{\sin }^2\theta =0\\ -r{\left(\frac{d\phi }{dt}\right)}^2\sin \theta ·\cos \theta =\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^3}{r}^2\sin \theta \frac{d\phi }{dt}\\ 2\frac{dr}{dt}\frac{d\phi }{dt}\sin \theta +r\frac{d^2\phi }{d{t}^2}\sin \theta =0\end{array}\\ \{\begin{array}{l}\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\phi }{dt}\right)}^2{\sin }^2\theta =0\\ \frac{d\phi }{dt}=-\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^2\cos \theta },\frac{d\phi }{dt}=-\frac{C}{r^2}\\ 2\frac{dr}{dt}\frac{d\phi }{dt}+r\frac{d^2\phi }{d{t}^2}=0\end{array}\end{array}}$

Combinamos la primera y segunda ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d}{dt}{\left(\frac{dr}{dt}\right)}^2=2\frac{dr}{dt}\frac{d^{2}r}{d{t}^2}=2\frac{dr}{dt}r{\left(\frac{d\phi }{dt}\right)}^2{\sin }^2\theta =2\frac{dr}{dt}r\frac{C^2}{r^4}{\sin }^2\theta =C^2{\sin }^2\theta ·\frac{2\frac{dr}{dt}}{r^3}=-C^2{\sin }^2\theta ·\left(\frac{d}{dt}\frac{1}{r^2}\right)\\ \frac{d}{dt}\left({\left(\frac{dr}{dt}\right)}^2+\frac{C^2{\sin }^2\theta }{r^2}\right)=0\\ \frac{d}{dt}\left({\left(\frac{dr}{dt}\right)}^2+r^4{\left(\frac{d\phi }{dt}\right)}^2\frac{{\sin }^2\theta }{r^2}\right)=0\\ \frac{d}{dt}\left({\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\phi }{dt}\right)}^2{\sin }^2\theta \right)=0\\ \frac{d{v}^2}{dt}=\mathrm{0,}{v}^2=\text{cte}\end{array}}$

Resultado que hemos obtenido anteriormente. Nos queda por resolver la segunda ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d\phi }{dt}=-\frac{{\mu }_0}{4\pi }\frac{q{q}_m}{m}\frac{1}{r^2\cos \theta }=\frac{J}{m{r}^2}\\ {\displaystyle \underset{0}{\overset{\phi }{\int }}d\phi }=\frac{J}{m}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{dt}{v^2{t}^2+r_0^2}}\\ \phi =\frac{J}{m}\frac{1}{v^2}\frac{v}{r_0}\arctan \left(\frac{vt}{r_0}\right)\\ \phi =\frac{J}{mv{r}_0}\arctan \left(\frac{vt}{r_0}\right)\end{array}}$

Resumiendo

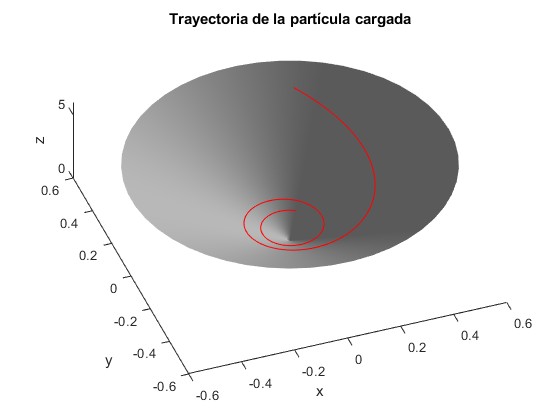
• La trayectoria de la partícula cargada reside en la superficie de un cono de ángulo 2θ, en cuyo vértice se encuentra el monopolo

${\displaystyle \sin \theta =\frac{mv{r}_0}{J}}$

• La distancia radial r de la partícula cargada al monopolo es

${\displaystyle r^2=v^2{t}^2+r_0^2}$

• El ángulo φ de la partícula cargada en función del tiempo t es

${\displaystyle \phi =\frac{J}{mv{r}_0}\arctan \left(\frac{vt}{r_0}\right)}$

v es el módulo de la velocidad de la partícula, una constante del movimiento

Datos

• Constante, J/m=1.002
• Módulo de la velocidad de la partícula cargada, v=0.1
• Distancia mínima al monopolo, r₀=1

v=0.1;
r0=1;
J=1.002;

theta=asin(v*r0/J);
r=linspace(0,6,50);
phi=linspace(0,2*pi,50);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
disp(z(end))
hold on
surfl(x,y,z);
shading interp
colormap(gray);
t=1:0.1:50;
phi=atan(v*t/r0)*J/(v*r0);
r=r0./cos(v*r0*phi/J);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
plot3(x,y,z,'r')
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Trayectoria de la partícula cargada')
view(-20,70)

Referencias

Anderson L. de Jesus, Alexandre G.M. Schmidt, Licinio L. S. Portugal. Introdução à Física do Monopolo Magnético: uma abordagem clássica. Revista Brasileira de Ensino de Física, vol. 45, e20220335 (2023)

I. Richard Lapidus, Jerry L. Pietenpol. Classical Interaction of an Electric Charge with a Magnetic Monopole. Am. J. Phys. 28, (1960), pp. 17-18