Movimiento de una partícula cargada en un campo magnético no uniforme

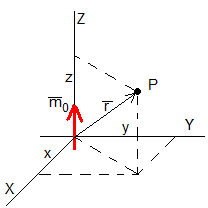
Una partícula de masa M y carga q se mueve en el campo magnético producido por un dipolo situado en el origen de momento $\overrightarrow{m}=m_0\widehat{k}$. El campo magnético producido por el dipolo tiene las expresión

${\displaystyle \overrightarrow{B}=\frac{{\mu }_0}{4\pi }\frac{3\left(\overrightarrow{m}·\overrightarrow{r}\right)\overrightarrow{r}-r^2\overrightarrow{m}}{r^5}}$

La partícula cargada en el instante t está en el punto P cuyo vector posición es $\overrightarrow{r}$.

${\displaystyle \begin{array}{l}\overrightarrow{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}\\ \overrightarrow{B}=\frac{{\mu }_0{m}_0}{4\pi }\frac{3xz\widehat{i}+3zy\widehat{j}+\left(2z^2-y^2-x^2\right)\widehat{k}}{r^5}\end{array}}$

En los puntos del plano XY (z=0) distantes r₀ del origen, el campo magnético vale

${\displaystyle {\overrightarrow{B}}_0=-\frac{{\mu }_0{m}_0}{4\pi }\frac{r_0^2}{r_0^5}\widehat{k}=-\frac{{\mu }_0{m}_0}{4\pi }\frac{1}{r_0^3}\widehat{k}}$

La expresión del campo magnético $\overrightarrow{B}$ en términos del módulo B₀ es

${\displaystyle \overrightarrow{B}=B_0{r}_0^3\frac{3xz\widehat{i}+3zy\widehat{j}+\left(2z^2-y^2-x^2\right)\widehat{k}}{r^5}}$

La fuerza que ejerce el campo magnético sobre la partícula cargada es

${\displaystyle \begin{array}{l}\overrightarrow{F}=q\overrightarrow{v}\times \widehat{B}=\\ q{B}_0\frac{r_0^3}{r^5}\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ \frac{dx}{dt}& \frac{dy}{dt}& \frac{dz}{dt}\\ 3xz& 3yz& 2z^2-y^2-x^2\end{array}\right|=\\ q{B}_0\frac{r_0^3}{r^5}\left\{\left(\left(2z^2-y^2-x^2\right)\frac{dy}{dt}-3yz\frac{dz}{dt}\right)\widehat{i}-\left(\left(2z^2-y^2-x^2\right)\frac{dx}{dt}-3xz\frac{dz}{dt}\right)\widehat{j}+\left(3yz\frac{dx}{dt}-3xz\frac{dy}{dt}\right)\widehat{k}\right\}\end{array}}$

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}M\frac{d^{2}x}{d{t}^2}=q{B}_0\frac{r_0^3}{r^5}\left(\left(2z^2-y^2-x^2\right)\frac{dy}{dt}-3yz\frac{dz}{dt}\right)\\ M\frac{d^{2}y}{d{t}^2}=-q{B}_0\frac{r_0^3}{r^5}\left(\left(2z^2-y^2-x^2\right)\frac{dx}{dt}-3xz\frac{dz}{dt}\right)\\ M\frac{d^{2}z}{d{t}^2}=q{B}_0\frac{r_0^3}{r^5}\left(3yz\frac{dx}{dt}-3xz\frac{dy}{dt}\right)\end{array}}$

Definimos nuevas variables: ω=|q|B₀/M, X=x/r₀, Y=y/r₀, Z=z/r₀, τ=ωt

${\displaystyle \begin{array}{l}\frac{d^{2}X}{d{\tau }^2}=\frac{q}{\left|q\right|}\frac{1}{{\left(X^2+Y^2+Z^2\right)}^{5/2}}\left(\left(2Z^2-Y^2-X^2\right)\frac{dY}{d\tau }-3YZ\frac{dZ}{d\tau }\right)\\ \frac{d^{2}Y}{d{\tau }^2}=-\frac{q}{\left|q\right|}\frac{1}{{\left(X^2+Y^2+Z^2\right)}^{5/2}}\left(\left(2Z^2-Y^2-X^2\right)\frac{dX}{d\tau }-3XZ\frac{dZ}{d\tau }\right)\\ \frac{d^{2}Z}{d{t}^2}=\frac{q}{\left|q\right|}\frac{3Z}{{\left(X^2+Y^2+Z^2\right)}^{5/2}}\left(Y\frac{dX}{d\tau }-X\frac{dY}{d\tau }\right)\end{array}}$

Dado que la fuerza F no realiza trabajo por ser perpendicular al desplazamiento, la energía cinética se mantiene constante

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}M\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)\\ {\left(\frac{dX}{dt}\right)}^2+{\left(\frac{dY}{dt}\right)}^2+{\left(\frac{dZ}{dt}\right)}^2=\text{cte}\end{array}}$

Supondremos que la partícula cargada es positiva, q/|q|=1. Resolvemos el sistema de tres ecuaciones diferenciales por procedimientos numéricos, con las siguientes condiciones iniciales

${\displaystyle t=0\{\begin{array}{l}X=\mathrm{1,}\left(\frac{dX}{dt}\right)=0.005\\ Y=\mathrm{1,}\left(\frac{dY}{dt}\right)=0.005\\ Z=\mathrm{0,}\left(\frac{dZ}{dt}\right)=0.01\end{array}}$

Para verificar el procedimiento numérico comparamos la energía cinética inicial E₀ de la partícula, y la final, E_f. El error cometido es

${\displaystyle \begin{array}{l}E\text{=}{\left(\frac{dX}{dt}\right)}^2+{\left(\frac{dY}{dt}\right)}^2+{\left(\frac{dZ}{dt}\right)}^2\\ \left|\frac{E_f-E_0}{E_0}\right|\times 100\end{array}}$

Para observar el movimiento de la partícula se precisa de mucho tiempo, el error acumulado veremos que es importante.

f=@(t,x) [x(2); ((2*x(5)^2-x(3)^2-x(1)^2)*x(4)
-3*x(3)*x(5)*x(6))/(x(1)^2+x(3)^2+x(5)^2)^(5/2); x(4); 
-((2*x(5)^2-x(3)^2-x(1)^2)*x(2)-3*x(1)*x(5)*x(6))/(x(1)^2+x(3)^2+x(5)^2)^(5/2); 
x(6); 3*x(5)*(x(3)*x(2)-x(1)*x(4))/(x(1)^2+x(3)^2+x(5)^2)^(5/2)];
[t,x]=ode45(f,[0,1328],[1,0.005, 1,0.005, 0,0.01]);
 plot(t,x(:,5))
 E0=x(1,2).^2+x(1,4).^2+x(1,6).^2;
 Ef=x(end,2).^2+x(end,4).^2+x(end,6).^2;
 error=abs((Ef-E0)/E0)*100;
 fprintf('Error %1.3f\n',error)
 grid on
 xlabel('\tau')
 ylabel('Z');
 title('Movimiento en un dipolo magnético')

Para observar el movimiento en el eje X e Y, se toma un τ_máx=25 850

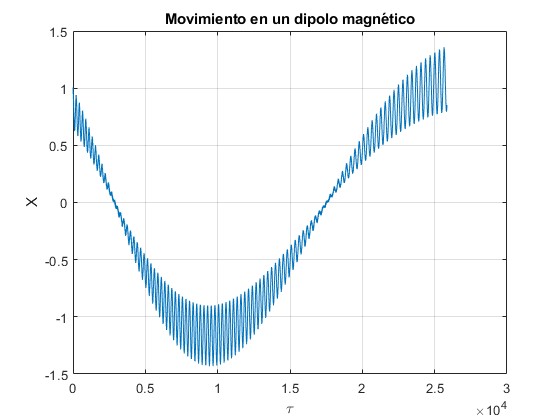
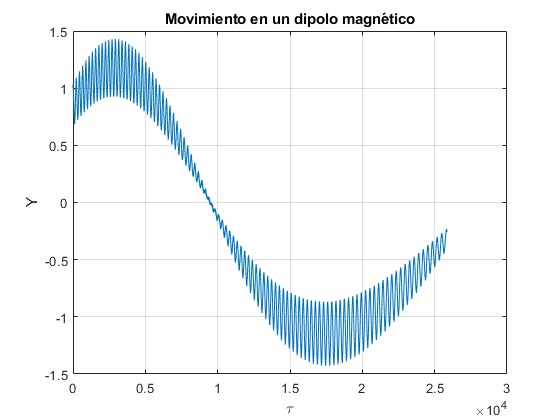
Error 49.568

Un error de casi el 50% es importante

Estas dos representaciones gráficas sugieren que hay dos periodos o tiempos característicos del movimiento: uno corto y otro mucho más largo, del valor medio de la posición X o Y de la partícula

Para observar el movimiento en el eje Z , se toma un τ_máx=1 328

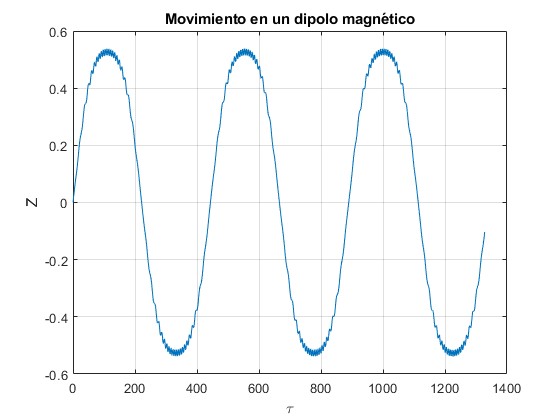
Error 4.770

Otro periodo lo observamos en el movimiento de la partícula a lo largo del eje Z

Representamos la trayectoria de la partícula cargada, cambiando las líneas de código por éstas

...
plot3(x(:,1),x(:,3),x(:,5))
grid on
xlabel('X')
ylabel('Y');
zlabel('Z');
title('Movimiento en un dipolo magnético')

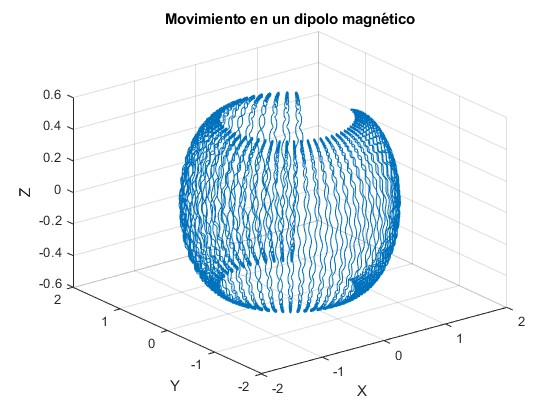
Movimiento de una partícula cargada en un campo magnético no uniforme

Una partícula de masa m y carga q se mueve en un campo magnético no uniforme

${\displaystyle \overrightarrow{B}=-\alpha yB\widehat{j}+(1+\alpha z)B\widehat{k}}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{d^2\overrightarrow{r}}{d{t}^2}=q\overrightarrow{v}\times \overrightarrow{B}\\ \frac{d^2\overrightarrow{r}}{d{t}^2}=\frac{qB}{m}\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ \frac{dx}{dt}& \frac{dy}{dt}& \frac{dz}{dt}\\ 0& -\alpha y& (1+\alpha z)\end{array}\right|\end{array}}$

Que da lugar a un sistema de tres ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=\omega \left((1+\alpha z)\frac{dy}{dt}+\alpha y\frac{dz}{dt}\right)\\ \frac{d^{2}y}{d{t}^2}=-\omega (1+\alpha z)\frac{dx}{dt}\\ \frac{d^{2}z}{d{t}^2}=-\omega \alpha y\frac{dx}{dt}\end{array}}$

con ω=qB/m. La primera ecuación diferencial se puede integrar

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\omega \frac{dy}{dt}+\omega \alpha \frac{d(y·z)}{dt}\\ \frac{dx}{dt}=\omega (1+\alpha z)y+C\end{array}}$

Donde C es una constante de integración que determinaremos a partir de las condiciones iniciales en el instante t=0

Conocido dx/dt, las otras dos ecuaciones diferenciales se expresan

${\displaystyle \{\begin{array}{l}\frac{d^{2}y}{d{t}^2}=-{\omega }^2{\left(1+\alpha z\right)}^{2}y-\omega C(1+\alpha z)\\ \frac{d^{2}z}{d{t}^2}=-{\omega }^2(1+\alpha z)\alpha y^2-\omega \alpha Cy\end{array}}$

Tenemos, por tanto, un sistema formado por una ecuación diferencial de primer orden y de dos ecuaciones diferenciales de segundo orden, que vamos a expresar de forma adimensional. Multiplicamos la primera ecuación diferencial por α/ω, la segunda y tercera por α/ω², y expresamos las ecuaciones diferenciales en términos de X=α·x, Y=α·y, Z=α·z, τ=ω·t y D=αC/ω

${\displaystyle \{\begin{array}{l}\frac{dX}{d\tau }=(1+Z)Y+D\\ \frac{d^{2}Y}{d{\tau }^2}=-{\left(1+Z\right)}^{2}Y-D(1+Z)\\ \frac{d^{2}Z}{d{\tau }^2}=-(1+Z)Y^2-DY\end{array}}$

Resolvemos este sistema de ecuaciones diferenciales con las siguientes condiciones iniciales: En el instante τ=0, la posición inicial es X=0, Y=Y₀, X=0, la velocidad inicial es dX/dτ=U_x, dY/dτ=0, dZ/dτ=U_z.

La constante de integración D que aprece en la primera ecuación diferencial, se determina a partir de las condiciones iniciales, en el instante τ=0, U_x=Y₀+D

Resultados

Sea Y₀=0.66, U_x=0.02, U_z=0.08. Resolvemos el sistema de ecuaciones diferenciales hasta el tiempo τ=140

• Coordenada X en función del tiempo τ

%X=x(1), Y=x(2), dY/dt=x(3), Z=x(4), dZ/dt=x(5)
x0=[0, 0.66, 0, 0, 0.08]; %condiciones iniciales
tf=140; %tiempo final
D=0.02-x0(2); %constante de integración
fg=@(t,x)[(1+x(4))*x(2)+D; x(3); -(1+x(4))^2*x(2)-D*(1+x(4)); 
x(5); -(1+x(4))*x(2)^2-D*x(2)];
[t,x]=ode45(fg,[0,tf],x0);
plot(t,x(:,1))
grid on
xlabel('\tau')
ylabel('X');
title('X en función de \tau')



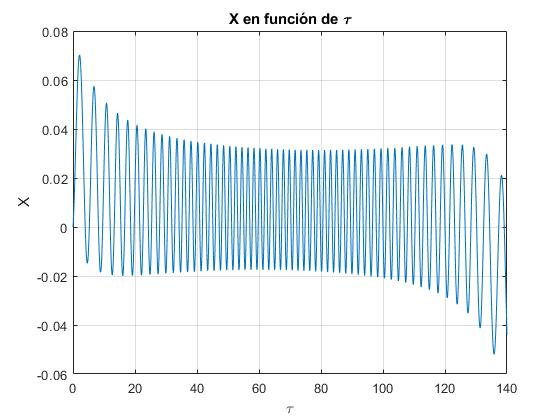
Comprobamos que la energía de la partícula se mantiene constante, ya que la fuerza que ejerce el campo magnético $\overrightarrow{F}=q\overrightarrow{v}\times \overrightarrow{B}$ es siempre perpendicular al desplazamiento $\overrightarrow{dr}$ de la partícula

${\displaystyle {\left(\frac{dX}{d\tau }\right)}^2+{\left(\frac{dY}{d\tau }\right)}^2+{\left(\frac{dZ}{d\tau }\right)}^2=U_x^2+U_z^2}$

>> ((1+x(:,4)).*x(:,2)+D).^2+x(:,3).^2+x(:,5).^2
ans =
    0.0068
    0.0068      
    ......   
    0.0067
    0.0067
    0.0067
>> 0.02^2+0.08^2
ans =    0.0068 

• Coordenada Y en función del tiempo τ

%X=x(1), Y=x(2), dY/dt=x(3), Z=x(4), dZ/dt=x(5)
x0=[0, 0.66, 0, 0, 0.08]; %condiciones iniciales
tf=140; %tiempo final
D=0.02-x0(2); %constante de integración
fg=@(t,x)[(1+x(4))*x(2)+D; x(3); -(1+x(4))^2*x(2)-D*(1+x(4)); 
x(5); -(1+x(4))*x(2)^2-D*x(2)];
[t,x]=ode45(fg,[0,tf],x0);
plot(t,x(:,2))
grid on
xlabel('\tau')
ylabel('Y');
title('Y en función de \tau')



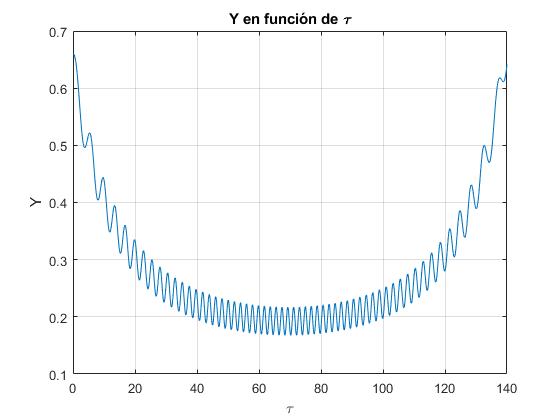
• Coordenada Z en función del tiempo τ

%X=x(1), Y=x(2), dY/dt=x(3), Z=x(4), dZ/dt=x(5)
x0=[0, 0.66, 0, 0, 0.08]; %condiciones iniciales
tf=140; %tiempo final
D=0.02-x0(2); %constante de integración
fg=@(t,x)[(1+x(4))*x(2)+D; x(3); -(1+x(4))^2*x(2)-D*(1+x(4)); 
x(5); -(1+x(4))*x(2)^2-D*x(2)];
[t,x]=ode45(fg,[0,tf],x0);
plot(t,x(:,4))
grid on
xlabel('\tau')
ylabel('Z');
title('Z en función de \tau')



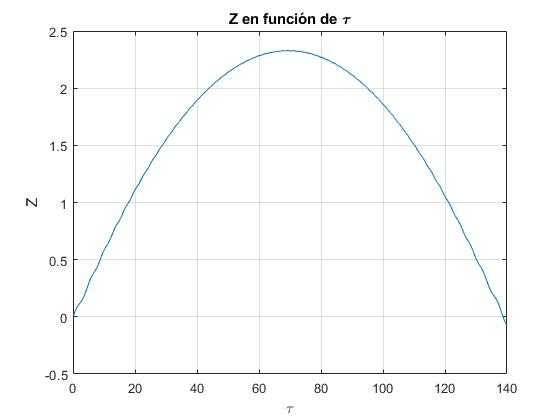
La coordenada Z alcanza un máximo Z_m=2.33 en el tiempo τ_m=69.3

>> [xmax, nmax]=max(x(:,4))
xmax =    2.3292
nmax =   858
>> t(nmax)
ans =   69.2907

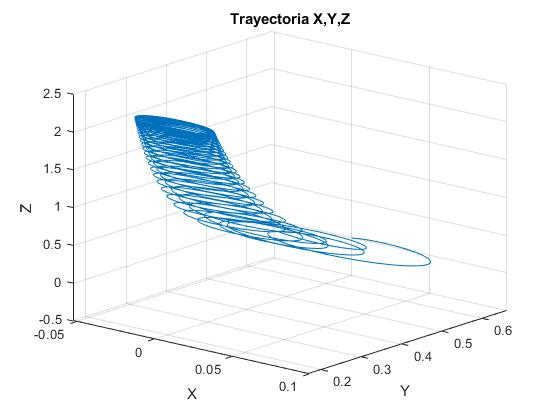
• La trayectoria en el espacio X, Y, Z

%X=x(1), Y=x(2), dY/dt=x(3), Z=x(4), dZ/dt=x(5)
x0=[0, 0.66, 0, 0, 0.08]; %condiciones iniciales
tf=140; %tiempo final
D=0.02-x0(2); %constante de integración
fg=@(t,x)[(1+x(4))*x(2)+D; x(3); -(1+x(4))^2*x(2)-D*(1+x(4)); 
x(5); -(1+x(4))*x(2)^2-D*x(2)];
[t,x]=ode45(fg,[0,tf],x0);
plot3(x(:,1),x(:,2),x(:,4))
grid on
xlabel('X')
ylabel('Y');
zlabel('Z')
title('Trayectoria X,Y,Z')
view(40,20)



• La trayectoria en el plano Z, Y

%X=x(1), Y=x(2), dY/dt=x(3), Z=x(4), dZ/dt=x(5)
x0=[0, 0.66, 0, 0, 0.08]; %condiciones iniciales
tf=140; %tiempo final
D=0.02-x0(2); %constante de integración
fg=@(t,x)[(1+x(4))*x(2)+D; x(3); -(1+x(4))^2*x(2)-D*(1+x(4)); 
x(5); -(1+x(4))*x(2)^2-D*x(2)];
[t,x]=ode45(fg,[0,tf],x0);
plot(x(:,4),x(:,2))
%plot(x(:,1),x(:,2))
grid on
xlabel('Z')
ylabel('Y');
title('Trayectoria Z,Y')



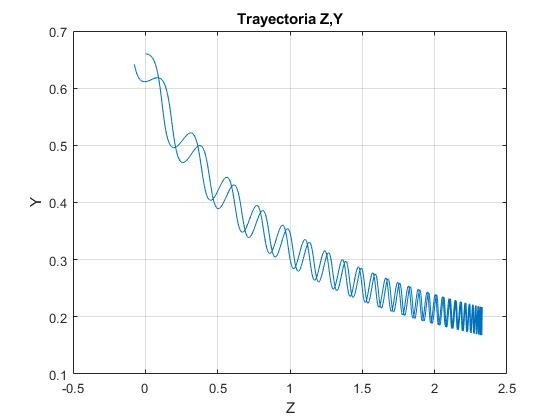
La partícula cargada se refleja en el instante τ_m en la posición Z_m

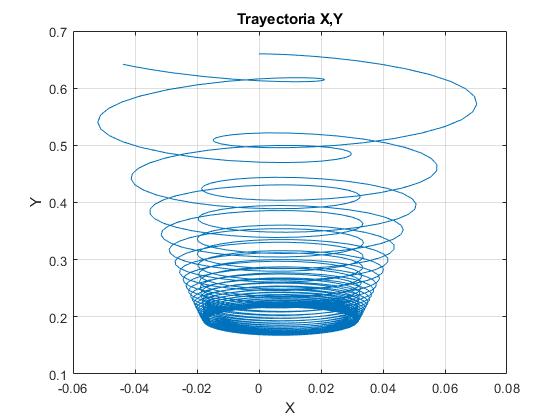
• La trayectoria en el plano X, Y

%X=x(1), Y=x(2), dY/dt=x(3), Z=x(4), dZ/dt=x(5)
x0=[0, 0.66, 0, 0, 0.08]; %condiciones iniciales
tf=140; %tiempo final
D=0.02-x0(2); %constante de integración
fg=@(t,x)[(1+x(4))*x(2)+D; x(3); -(1+x(4))^2*x(2)-D*(1+x(4)); 
x(5); -(1+x(4))*x(2)^2-D*x(2)];
[t,x]=ode45(fg,[0,tf],x0);
plot(x(:,1),x(:,2))
grid on
xlabel('X')
ylabel('Y');
title('Trayectoria X,Y')

Referencias

J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Questions 4.22, 4.23, pp. 231-234.

O. L. de Lange, J. Pierrus Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Question 7.23, pp. 201-205