En una mañana fría cuando está rociando, observamos gotas del vapor de agua condensado en las hierbas, en las hojas de las plantas, en las telas de araña. Nos fijamos en las pequeñas gotas casi esféricas sobre la superficie de algunas hojas.

Antes de proceder al estudio de este tema complejo recordaremos un concepto geométrico

Area lateral de un cono truncado

Empezamos por el área lateral de un cono de radio r de la base y altura H

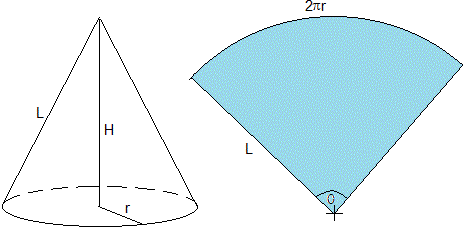
Supongamos que el cono está hecho de papel, cortamos el cono a lo largo de su generatriz y lo extendemos sobre una superficie plana, obtenemos un sector circular de radio L (generatriz) y ángulo θ=2πr/L. El área A de este sector circular es

${\displaystyle A=\pi rL=\pi r\sqrt{H^2+r^2}}$

Sea un tronco de cono cuyas bases tiene radios b (mayor) y a (menor) y altura h

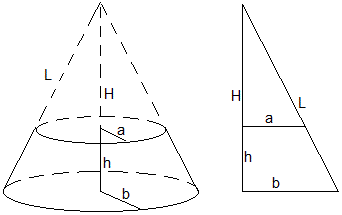
El área lateral del tronco de cono es la diferencia entre la de un cono de radio base b y altura H y la del cono de radio base a y altura H-h, tal como se muestra en la figura.

${\displaystyle A=\pi b\sqrt{H^2+b^2}-\pi a\sqrt{{\left(H-h\right)}^2+a^2}}$

En los dos triángulos rectángulos, establecemos las relaciones H=bh/(b-a) y H-h=ah/(b-a). La expresión del área A se simplifica notablemente

${\displaystyle A=\pi (a+b)\sqrt{h^2+{\left(b-a\right)}^2}}$

Una gota de líquido sobre un plano horizontal

Cuando una gota de líquido se coloca sobre una superficie horizontal, la fuerza de la gravedad tiende a extenderla para reducir la energía potencial gravitatoria, mientras que la tensión superficial tiende a juntar el líquido para reducir la energía superficial. La forma de equilibrio de la gota será aquella que haga mínimo la suma de las energías superficial y gravitatoria. Más adelante, deduciremos las ecuaciones diferenciales que describen la forma de la gota aplicando el cálculo de variaciones.

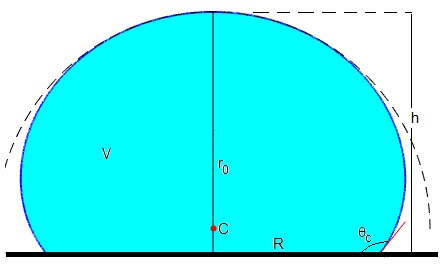
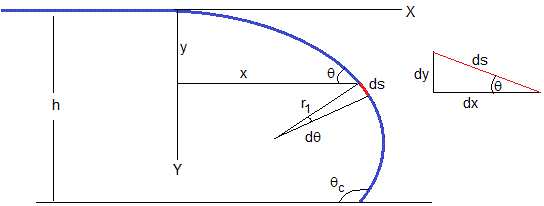
La forma de la gota es una superficie de revolución alrededor del eje vertical Y, utilizaremos dos funciones x=x(θ) e y=y(θ) dependientes de un parámetro θ para describirla. Los datos de partida son el volumen V de la gota y la altura h de la cúspide sobre la superficie horizontal. A partir de estos datos, dibujaremos el perfil de la gota y calcularemos el ángulo de contacto θ_c y el radio R de la base de la gota.

Otro parámetro inicial importante es el radio de curvatura r₀ de la cúspide. La línea a trazos es la circunferencia de radio r₀ a la que se aproxima la cúspide, cuyo centro se encuentra en el punto de color rojo C

El volumen V de la gota y la altura h se pueden medir fácilmente, sin embargo, la curvatura r₀ es muy difícil de medir, así como el radio R de la base debido a las imperfecciones inevitables de la superficie horizontal

Angulo de contacto

El ángulo de contacto, θ_c que forma la superficie de la gota con el plano horizontal, es independiente del volumen de la gota, como comprobaremos al final de la página.

Calculamos la presión a la altura y, debida:

• a la curvatura r₀ de la superficie de la gota en la cúspide, γ(1/r₀+1/r₀)=2γ/r₀ de acuerdo a la ecuación de Young-Laplace

• a una columna de fluido de altura y, ρgy

${\displaystyle p=\frac{2\gamma }{r_0}+\rho gy}$

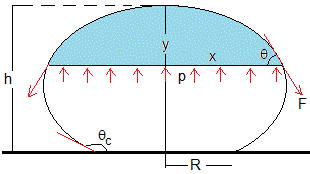
Las fuerzas que mantienen el equilibrio de la superficie circular de radio x situada a la altura y son:

• El peso mg, siendo m la masa de la región sombreada

• La presión p a la altura y, ejerce una fuerza sobre el círculo de radio x, p(πx²)

• La tensión superficial ejerce una fuerza F=γ(2πx) cuya dirección es tangencial. Su componente vertical es Fsinθ

El equilibrio de fuerzas en la dirección vertical a la altura y, se escribe

${\displaystyle mg+\gamma \left(2\pi x\right)\sin \theta =p\left(\pi x^2\right)}$

Si y=h, la región sombreada se extiende al volumen de la gota

${\displaystyle \rho Vg+\gamma \left(2\pi R\right)\sin {\theta }_c=\left(\frac{2\gamma }{r_0}+\rho gh\right)\left(\pi R^2\right)}$

ρ es la densidad del líquido y V el volumen de la gota

Despejamos el ángulo de contacto θ_c

${\displaystyle {\theta }_c=\arcsin \left(\frac{R}{r_0}+\left(Rh-\frac{V}{\pi R}\right)\frac{\rho g}{2\gamma }\right)}$

Equilibrio

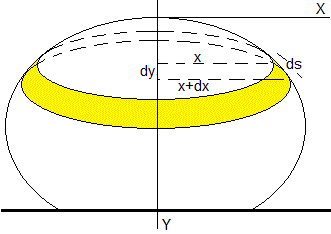
En este apartado, vamos a calcular las ecuaciones que describen el perfil de la gota a partir de las fuerzas que la mantienen en equilibrio sobre la superficie horizontal

En la figura, mostramos una gota situada sobre una superficie plana y horizontal. Debido a la simetría cilíndrica, situamos el origen en la cúspide de la gota, con el eje Y apuntando hacia abajo y el eje X en la dirección radial

Consideremos un elemento diferencial de gota comprendido entre los planos de alturas y e y+dy. El volumen de este elemento diferencial es πx²·dy y el volumen total V del líquido (supuesto incomprensible) en la gota es

${\displaystyle V={\displaystyle \underset{0}{\overset{h}{\int }}\pi x^{2}dy}}$

Consideremos ahora, su superficie lateral, pintada de color amarillo, corresponde a la de un tronco de cono de bases, b=x+dx, a=x y altura h=dy. El área lateral es

${\displaystyle dA=\pi \left(2x+dx\right)\sqrt{d{y}^2+d{x}^2}=2\pi xds}$

Consideremos las fuerzas sobre dicho elemento diferencial de superficie de la gota:

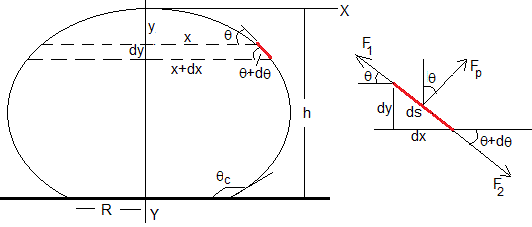
• La fuerza F_p debida a la presión sobre dicha superficie, es perpendicular a la misma F_p·dA. Su componente vertical Y es F_pcosθ=p·(2πx·ds)·cosθ=p·(2πx·dx)

${\displaystyle \left(\frac{2\gamma }{r_0}+\rho gy\right)2\pi x·dx}$

• La fuerza F₁ que ejerce la parte superior de la superficie de la gota sobre el elemento de superficie considerado, F₁=γ(2πx), cuya dirección es tangente a la superficie. Su proyección sobre el eje vertical Y es, γ(2πx)sinθ

• La fuerza F₂ que ejerce la parte inferior de la superficie de la gota sobre el elemento de superficie considerado, F₂=γ·2π(x+dx). Su proyección sobre el eje vertical Y es, γ·2π(x+dx)sin(θ+dθ)

En el equilibrio se ha de cumplir que

${\displaystyle \begin{array}{l}\left(\frac{2\gamma }{r_0}+\rho gy\right)2\pi x·dx+2\pi \gamma x\sin \theta =2\pi \gamma (x+dx)\sin (\theta +d\theta )\\ \left(\frac{2\gamma }{r_0}+\rho gy\right)2\pi x·dx+2\pi \gamma x\sin \theta =2\pi \gamma (x+dx)\left(\sin \theta +\cos \theta ·d\theta \right)\\ \left(\frac{2\gamma }{r_0}+\rho gy\right)2\pi x·dx=2\pi \gamma x\cos \theta ·d\theta +2\pi \gamma \sin \theta ·dx\end{array}}$

Despejando dx/dθ

${\displaystyle \frac{dx}{d\theta }=\frac{\gamma \cos \theta }{\frac{2\gamma }{r_0}+\rho gy-\gamma \frac{\sin \theta }{x}}}$

Integrando esta ecuación diferencial obtenemos la función x=x(θ). La otra ecuación diferencial se obtiene teniendo en cuenta que tanθ=dy/dx

${\displaystyle \frac{dy}{d\theta }=\frac{dy}{dx}\frac{dx}{d\theta }=\frac{\gamma \sin \theta }{\frac{2\gamma }{r_0}+\rho gy-\gamma \frac{\sin \theta }{x}}}$

Integrando esta ecuación diferencial obtenemos y=y(θ). De este modo, determinaremos y representaremos el perfil de la gota

Energía mínima

Una gota colocada sobre una superficie horizontal, tiene la forma que hace mínima la suma de la energía potencial gravitatoria y la energía superficial (recuérdese que la tensión superficial, γ, es la energía por unidad de área), manteniendo constante el volumen. En este apartado, vamos a utilizar el cálculo de variaciones, para resolver una situación similar al denominado problema isoperimétrico, otra situación similar es la tratada en la página titulada La forma que adopta una cuerda bajo la acción de su peso y de la tensión superficial

• Consideremos un elemento diferencial de gota comprendido entre los planos de alturas y e y+dy. El volumen de este elemento diferencial es πx²·dy. Su energía potencial gravitatoria es -(ρπx²·dy)gy. La energía potencial total de la gota es

${\displaystyle E_g={\displaystyle \underset{0}{\overset{h}{\int }}-\rho (\pi x^2·dy)gy}={\displaystyle \underset{0}{\overset{h}{\int }}-\rho g\pi x^{2}y}·dy}$

El nivel cero de referencia de la energía potencial lo situamos en el eje X

• Como la tensión superficial, γ, es la energía por unidad de área, la energía superficial del área de la superficie lateral 2πx·ds que rodea el elemento diferencial de volumen es γ2πx·ds. La energía superficial total de la gota es

${\displaystyle E_s={\displaystyle \underset{0}{\overset{s}{\int }}\gamma ·2\pi xds=}{\displaystyle \underset{0}{\overset{h}{\int }}\gamma ·2\pi x\sqrt{1+{\left(\frac{dx}{dy}\right)}^2}dy}}$

La suma de estas dos energías deberá ser mínima, con la condición de que el volumen V de la gota permanezca constante

${\displaystyle V={\displaystyle \underset{0}{\overset{h}{\int }}\pi x^{2}dy}}$

Formamos la función auxiliar dependiente del parámetro λ

${\displaystyle F(y,x,\dot{x})=-\rho g\pi x^{2}y+2\pi \gamma ·x\sqrt{1+{\left(\frac{dx}{dy}\right)}^2}+\lambda \pi x^2}$

Dado que la función F depende de y, x y dx/dy, la ecuación de Euler-Lagrange se escribe (se ha intercambiado x por y)

${\displaystyle \frac{\partial F}{\partial x}-\frac{d}{dy}\left(\frac{\partial F}{\partial \dot{x}}\right)=0}$

El resultado es

${\displaystyle \begin{array}{l}-\rho gxy+\gamma \sqrt{1+{\dot{x}}^2}+\lambda r-\lambda \left\{\frac{{\dot{x}}^2}{\sqrt{1+{\dot{x}}^2}}+\frac{x\ddot{x}}{{\left(1+{\dot{x}}^2\right)}^{3/2}}\right\}=0\\ \gamma \left(\frac{1}{\sqrt{1+{\dot{x}}^2}}-\frac{x\ddot{x}}{{\left(1+{\dot{x}}^2\right)}^{3/2}}\right)=\rho gxy-\lambda x\end{array}}$

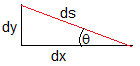
En vez de obtener la solución de la ecuación diferencial de segundo orden, vamos a reemplazarla por dos ecuaciones diferenciales de primer orden que nos da la solución en forma paramétrica, x=x(θ) e y=y(θ) para la forma de la gota

Expresamos la ecuación diferencial en términos del ángulo θ

${\displaystyle \begin{array}{l}\dot{x}=\frac{dx}{dy}=\frac{1}{\tan \theta }\\ \sqrt{1+{\dot{x}}^2}=\sqrt{1+{\left(\frac{dx}{dy}\right)}^2}=\frac{1}{\sin \theta }\\ \ddot{x}=\frac{d^{2}x}{d{y}^2}=\frac{d}{dy}\left(\frac{1}{\tan \theta }\right)=\frac{d}{d\theta }\left(\frac{1}{\tan \theta }\right)\frac{d\theta }{dy}=-\frac{1}{{\sin }^2\theta }\frac{d\theta }{dy}\end{array}}$

Sustituyendo en la ecuación diferencial de segundo orden

${\displaystyle \frac{dy}{d\theta }=\frac{\gamma \sin \theta }{\rho gy-\lambda -\gamma \frac{\sin \theta }{x}}}$

Integrando esta ecuación diferencial obtenemos y=y(θ)

Teniendo en cuenta que

${\displaystyle \begin{array}{l}\frac{dx}{d\theta }\frac{d\theta }{dy}=\frac{1}{\tan \theta }\\ \frac{dx}{d\theta }=\frac{1}{\tan \theta }\frac{dy}{d\theta }\end{array}}$

Obtenemos la segunda ecuación diferencial

${\displaystyle \frac{dx}{d\theta }=\frac{\gamma \cos \theta }{\rho gy-\lambda -\gamma \frac{\sin \theta }{x}}}$

Integrando esta ecuación diferencial obtenemos x=x(θ)

Ahora bien, en la cúspide de la gota, cuando x→0, y θ→0, en el denominador tenemos una indeterminación que se resuelve aplicando la regla de L'Hopital

${\displaystyle {\left(\frac{dx}{d\theta }\right)}_0=\frac{\gamma \cos 0}{-\lambda -\gamma \frac{\cos 0}{{\left(\frac{dx}{d\theta }\right)}_0}}}$

Despejamos la derivada dx/dθ en θ=0,

${\displaystyle {\left(\frac{dx}{d\theta }\right)}_0=-\frac{2\gamma }{\lambda }}$

Por otra parte, en la cúspide θ→0, se cumple (arco=radio·ángulo). Véase la primera figura

${\displaystyle {\left(\frac{dx}{d\theta }\right)}_0=r_0}$

Donde r₀ es el radio de curvatura de la cúspide. De este modo, hemos dado un significado al multiplicador, λ=-2γ/r₀.

Finalmente, volvemos a obtener las dos ecuaciones diferenciales que describen el perfil de la gota situada sobre una superficie horizontal

${\displaystyle \begin{array}{l}\frac{dy}{d\theta }=\frac{\gamma \sin \theta }{\rho gy+\frac{2\gamma }{r_0}-\gamma \frac{\sin \theta }{x}}\\ \frac{dx}{d\theta }=\frac{\gamma \cos \theta }{\rho gy+\frac{2\gamma }{r_0}-\gamma \frac{\sin \theta }{x}}\end{array}}$

Perfil de la gota

Este sistema de dos ecuaciones diferenciales no tiene solución analítica, por lo que integraremos, empleando procedimientos numéricos, el sistema de dos ecuaciones diferenciales para representar el perfil de la gota, partiendo de la cúspide θ=0, x=0 e y=0. Los datos de partida son el volumen V de la gota y la altura h de su cúspide

Sistema de unidades

Conocemos la densidad ρ y la tensión superficial γ del fluido. Para el agua ρ=1000 kg/m³ y γ=72·10^-3 N/m. Para que el ordenador no trabaje con números demasiado pequeños, establecemos un sistema de unidades en el que la longitud se mida en cm, la densidad ρ·1000 kg/m³ y la tensión superficial en γ·10^-3 N/m

${\displaystyle \begin{array}{l}\frac{dx·{10}^{-2}}{d\theta }=\frac{\gamma ·{10}^{-3}\cos \theta }{{10}^3·9.8·\rho ·y·{10}^{-2}+\frac{2·\gamma ·{10}^{-3}}{r_0·{10}^{-2}}-\gamma ·{10}^{-3}\frac{\sin \theta }{x·{10}^{-2}}}\\ \frac{dx}{d\theta }=\frac{\gamma \cos \theta }{980\rho y+\frac{2·\gamma }{r_0}-\gamma \frac{\sin \theta }{x}}\end{array}}$

Una expresión similar para dy/dθ

${\displaystyle \frac{dy}{d\theta }=\frac{\gamma \sin \theta }{980\rho y+\frac{2·\gamma }{r_0}-\gamma \frac{\sin \theta }{x}}}$

Indeterminación

La primera dificultad con la que nos tropezamos es que en la cúspide θ=0, x=0, y=0 se produce la indeterminación 0/0 en el término sinθ/x del denominador de las dos ecuaciones. Como hemos visto en el apartado anterior, para θ=0, las derivadas (dy/dθ)₀=0 y (dx/dθ)₀=r₀

No podemos utilizar el procedimiento ode45 de MATLAB, ya que produce un error NaN en la primera iteracción. Utilizaremos el procedimiento de Runge-Kutta descrito en el apartado titulado Sistema de dos ecuaciones diferenciales de primer orden para integrar el sistema de ecuaciones. Para evitar la indeterminación, separaremos la primera iteracción del resto

%sistema de dos ecuaciones diferenciales
f=@(t,x,y) gamma*cos(t)/(2*gamma/r0+rho*980*y-gamma*sin(t)/x);
g=@(t,x,y) gamma*sin(t)/(2*gamma/r0+rho*980*y-gamma*sin(t)/x);
x(1)=0; y(1)=0; %condiciones iniciales en la cúspide

%primera iteracción
i=1;
k1=dt*r0;
l1=0;
k2=dt*f(t(i)+dt/2,x(i)+k1/2,y(i)+l1/2);
l2=dt*g(t(i)+dt/2,x(i)+k1/2,y(i)+l1/2);
k3=dt*f(t(i)+dt/2,x(i)+k2/2,y(i)+l2/2);
l3=dt*g(t(i)+dt/2,x(i)+k2/2,y(i)+l2/2);
k4=dt*f(t(i)+dt,x(i)+k3,y(i)+l3);
l4=dt*g(t(i)+dt,x(i)+k3,y(i)+l3);     
x(i+1)=x(i)+(k1+2*k2+2*k3+k4)/6;
y(i+1)=y(i)+(l1+2*l2+2*l3+l4)/6;        

%segunda, tercera, n iteracciones
for i=2:n
        k1=dt*f(t(i),x(i),y(i));
        l1=dt*g(t(i),x(i),y(i));
        k2=dt*f(t(i)+dt/2,x(i)+k1/2,y(i)+l1/2);
        l2=dt*g(t(i)+dt/2,x(i)+k1/2,y(i)+l1/2);
        k3=dt*f(t(i)+dt/2,x(i)+k2/2,y(i)+l2/2);
        l3=dt*g(t(i)+dt/2,x(i)+k2/2,y(i)+l2/2);
        k4=dt*f(t(i)+dt,x(i)+k3,y(i)+l3);
        l4=dt*g(t(i)+dt,x(i)+k3,y(i)+l3);
        x(i+1)=x(i)+(k1+2*k2+2*k3+k4)/6;
        y(i+1)=y(i)+(l1+2*l2+2*l3+l4)/6;
        
        if y(i+1)>=h %completa la integración
            break;
        end
end

El procedimiento numérico termina en la iteracción i+1 cuando la ordenada y alcanza la posición h del plano horizontal, o altura de la gota. El número n de iteracciones deberá ser lo suficientemente grande para asegurarnos de que alcanzamos esta posición

Radio de curvatura de la cúspide

El sistema de dos ecuaciones diferenciales nos pide el radio de curvatura r₀ de la cúspide, pero este dato es muy difícil de obtener observando la gota sobre la superficie horizontal. Hacemos que r₀=h y calculamos el volumen V_c de la gota empleando el procedimiento numérico denominado fórmula del trapecio

${\displaystyle V_c={\displaystyle \underset{0}{\overset{h}{\int }}\pi x^{2}dy}}$

...
vol=0;
for j=1:i
     vol=vol+(y(j+1)-y(j))*(pi*x(j)^2+pi*x(j+1)^2)/2;
end
disp(['volumen: ', num2str(vol)]);

• Si el volumen V_c calculado es menor que el volumen dado V, se prueba un valor mayor de r₀

• Si V_c es mayor que V se prueba un valor menor de r₀.

El proceso se repite hasta que se alcance la precisión deseada.

Tenemos una ecuación transcedente V(r₀, h)-V=0, cuya solución buscamos aplicando el procedimiento de Newton-Raphson. Dado que no conocemos la función f(x)=V(x)-V=0 de forma explícita ni su derivada, el procedimiento a aplicar es

${\displaystyle x_{n+1}=x_n-\delta \frac{V(x_n)-V}{V(x_n+\delta )-V(x_n)}}$

donde δ es una cantidad pequeña

El proceso de convergencia se termina en un número N de pasos o cuando se alcanza la precisión deseada

${\displaystyle \left|\frac{x_{n+1}-x_n}{x_{n+1}}\right|<\epsilon }$

...
r0=h; %valor inicial; %cm
%rutina de convergencia hacia el valor r0 que hace que el volumen de la
%gota se aproxime a V
delta=0.0001;
N=20; %número de pasos
for i=1:N
    [R, th_c, V0, x, y,k]=forma_gota_ode(rho, gamma, h, r0);
    [R, th_c, Vc, x, y,k]=forma_gota_ode(rho, gamma, h, r0+delta);
    r1=r0-delta*(V0-V)/(Vc-V0);
    if abs((r1-r0)/r1)<0.001
        break;
    end
    r0=r1;
end
if(i==N)
    disp('No se alcanza la precisión deseada')
end

Radio base y ángulo de contacto

Se termina el proceso de integración de las dos ecuaciones diferenciales, cuando la ordenada y alcanza la posición h del plano horizontal, el procedimiento nos proporciona el radio R de la base y el ángulo de contacto

...
disp([y(i+1),x(i+1),t(i+1)*180/pi]) %altura, radio base, ángulo de contacto

Obtenemos, de forma alternativa, el ángulo de contacto mediante su expresión en el nuevo sistema de unidades establecido

${\displaystyle \begin{array}{l}{\theta }_c=\arcsin \left(\frac{R}{r_0}+\left(Rh-\frac{V}{\pi R}\right)\frac{\rho g}{2\gamma }\right)\\ {\theta }_c=\arcsin \left(\frac{R·{10}^{-2}}{r_0·{10}^{-2}}+\left(Rh·{10}^{-4}-\frac{V·{10}^{-6}}{\pi R·{10}^{-2}}\right)\frac{{10}^3\rho 9.8}{2\gamma ·{10}^{-3}}\right)\\ {\theta }_c=\arcsin \left(\frac{R}{r_0}+\left(Rh-\frac{V}{\pi R}\right)\frac{980\rho }{2\gamma }\right)\end{array}}$

Hay dos posibles ángulos suplementarios, θ_c y π-θ_c

R=x(i+1);  %radio de la base
th_c=asin(R/r0+(R*h-V/(pi*R))*980*rho/(2*gamma));
disp((pi-th_c)*180/pi) %ángulo suplementario

El código

En primer lugar, proporcionamos los datos de:

• la tensión superficial, γ
• densidad del líquido, ρ
• volumen de líquido,V
• altura de la cúspide sobre el plano horizontal, h en el sistema de unidades establecido
• valor inicial del radio de curvatura de la cúspide, una buena elección es, r₀=h

gamma=72; %tensión superficial
rho=1; %g/cm^3
%unidades para que x e y se midan en cm
V=0.04; %cm^3
h=0.3; %cm
r0=h; %cm

Creamos una función forma_gota_ode, a la que pasamos la densidad ρ, la la tensión superficial γ, la altura de la cúspide sobre el plano horizontal h, y el radio de curvatura de la cúspide r₀.

La función devuelve:

• el radio de la base de la gota, R
• el ángulo de contacto, θ_c
• el volumen calculado V_c de la gota
• los vectores x e y que determinan los puntos de abscisa x(i) y ordenada y(i), i=1,2,...k, que describen el perfil de la gota
• El tamaño de los vectores es el número k de iteracciones

Como el perfil de la gota es simétrico respecto del eje vertical Y, se calcula solamente la parte derecha

function [R, th_c, Vc, x, y, k] =forma_gota_ode(rho, gamma, h, r0)
    %sistema de dos ecuaciones diferenciales
    f=@(t,x,y) gamma*cos(t)/(2*gamma/r0+rho*980*y-gamma*sin(t)/x);
    g=@(t,x,y) gamma*sin(t)/(2*gamma/r0+rho*980*y-gamma*sin(t)/x);
    n=31415; %número máximo de iteracciones
    dt=pi/n; %paso
    t=0:dt:pi;
%reserva memoria para n+1 elementos de los vectores x e y
    x=zeros(n+1,1); 
    y=zeros(n+1,1);
    x(1)=0; y(1)=0; %condiciones iniciales
    
    %primera iteracción
    i=1;
    k1=dt*r0;
    l1=0;
    k2=dt*f(t(i)+dt/2,x(i)+k1/2,y(i)+l1/2);
    l2=dt*g(t(i)+dt/2,x(i)+k1/2,y(i)+l1/2);
    k3=dt*f(t(i)+dt/2,x(i)+k2/2,y(i)+l2/2);
    l3=dt*g(t(i)+dt/2,x(i)+k2/2,y(i)+l2/2);
    k4=dt*f(t(i)+dt,x(i)+k3,y(i)+l3);
    l4=dt*g(t(i)+dt,x(i)+k3,y(i)+l3);     
    x(i+1)=x(i)+(k1+2*k2+2*k3+k4)/6;
    y(i+1)=y(i)+(l1+2*l2+2*l3+l4)/6;  
    %resto de las iteracciones
    for i=2:n
        k1=dt*f(t(i),x(i),y(i));
        l1=dt*g(t(i),x(i),y(i));
        k2=dt*f(t(i)+dt/2,x(i)+k1/2,y(i)+l1/2);
        l2=dt*g(t(i)+dt/2,x(i)+k1/2,y(i)+l1/2);
        k3=dt*f(t(i)+dt/2,x(i)+k2/2,y(i)+l2/2);
        l3=dt*g(t(i)+dt/2,x(i)+k2/2,y(i)+l2/2);
        k4=dt*f(t(i)+dt,x(i)+k3,y(i)+l3);
        l4=dt*g(t(i)+dt,x(i)+k3,y(i)+l3);
        x(i+1)=x(i)+(k1+2*k2+2*k3+k4)/6;
        y(i+1)=y(i)+(l1+2*l2+2*l3+l4)/6;
        %final del proceso de integración numérica
        if y(i+1)>=h 
            break;
        end
    end
    k=i+1; %iteracción final
    R=x(k); %radio de la base de la gota
    th_c=t(k); %ángulo de contacto
  
  %volumen calculado de la gota 
    Vc=0;
    for j=1:k-1
        Vc=Vc+(y(j+1)-y(j))*(pi*x(j)^2+pi*x(j+1)^2)/2;
    end
 end

Comparamos el volumen calculado V_c con el volumen dado V y modificamos el valor de r₀, repetimos el proceso hasta alcanzar la precisión deseada. Una vez alcanzada, representmos el perfil de la gota y proporcionamos los parametros más importantes: ángulo de contacto θ_c, radio de la base R, radio de curvatura de la cúspide r₀

...
%gráficos
hold on
fill([-fliplr(x(1:k));0],[-fliplr(y(1:k));-h],'c')
fill([0;x(1:k)],[-h;-y(1:k)],'c')
plot([-fliplr(x(1:k)), x(1:k)],[-fliplr(y(1:k)),-y(1:k)],'b','lineWidth',1.5)
text(0,-h/2,num2str(r0)) %radio curvatura
text(R/2,-h+0.02,num2str(R)) %radio base
line([-R-0.05, R+0.05],[-h,-h],'lineWidth',1.5,'color','k')
line([R,R+0.05*cos(pi-th_c)], [-h, -h+0.05*sin(pi-th_c)],'color','r')
text(R,-h-0.01,num2str(th_c*180/pi)) %ángulo de contacto
hold off
axis equal
xlabel('x')
ylabel('y')
title('Forma de la gota de agua')

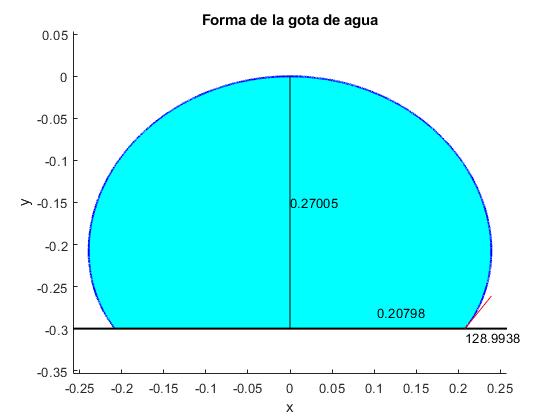
Cambiando el volumen V y la altura h, probamos que el ángulo de contacto θ_c es independiente del volumen

Con el mismo el volumen V=0.04, cambiamos la altura h=0.195 cm de la cúspide de la gota. El resultado es

gamma=72; %tensión superficial
rho=1; %g/cm^3
%unidades para que x e y se midan en cm
V=0.04; %cm^3
h=0.195; %cm
r0=h; %valor inicial; %cm
....

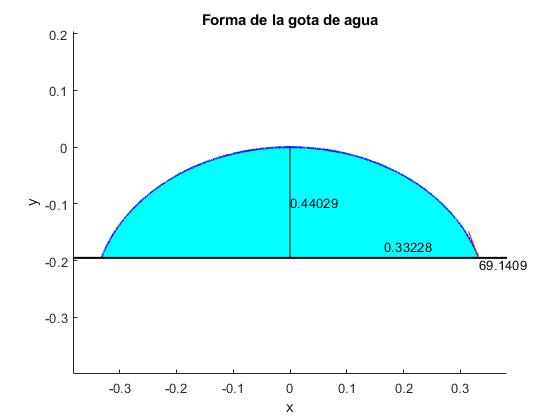
Cambiando el volumen V y la altura h, probamos que el ángulo de contacto θ_c es independiente del volumen

El programa completo consta de la función forma_gota_ode (en color rosa, más arriba) y del script

gamma=72; %tensión superficial
rho=1; %g/cm^3
%unidades para que x e y se midan en cm
V=0.04; %cm^3
h=0.3; %cm
r0=h; %valor inicial; %cm

%rutina de convergencia hacia el valor r0 que hace que el volumen de la
%gota se aproxime a V
delta=0.0001;
N=20; %número de pasos
for i=1:N
    [R, th_c, V0, x, y,k]=forma_gota_ode(rho, gamma, h, r0);
    [R, th_c, Vc, x, y,k]=forma_gota_ode(rho, gamma, h, r0+delta);
    r1=r0-delta*(V0-V)/(Vc-V0);
    if abs((r1-r0)/r1)<0.001
        break;
    end
    r0=r1;
end
if(i==N)
    disp('No se alcanza la precisión deseada')
end
   
%gráficos
hold on
fill([-fliplr(x(1:k));0],[-fliplr(y(1:k));-h],'c')
fill([0;x(1:k)],[-h;-y(1:k)],'c')
plot([-fliplr(x(1:k)), x(1:k)],[-fliplr(y(1:k)),-y(1:k)],'b','lineWidth',1.5)
text(0,-h/2,num2str(r0))
text(R/2,-h+0.02,num2str(R))
line([-R-0.05, R+0.05],[-h,-h],'lineWidth',1.5,'color','k')
line([R,R+0.05*cos(pi-th_c)], [-h, -h+0.05*sin(pi-th_c)],'color','r')
text(R,-h-0.01,num2str(th_c*180/pi))
hold off
axis equal
xlabel('x')
ylabel('y')
title('Forma de la gota de agua')

Medida de la tensión superficial. Método de Quincke

Consideremos una gota alargada sobre un superficie sólida horizontal perfectamente lisa. La parte superior de la gota es casi plana y está a una altura h sobre la superficie sólida y forma un ángulo de contacto θ_c tal como se aprecia en la figura. En una gota alargada, el radio de la base R es bastante mayor que la altura h

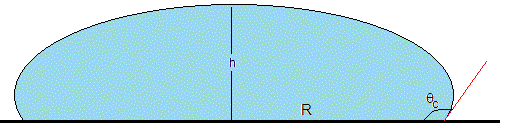
La ecuación de Young-Laplace afirma que

${\displaystyle \Delta p=\gamma \left(\frac{1}{r_1}+\frac{1}{r_2}\right)}$

Siendo r₁ y r₂ el radio mínimo y máximo de curvatura del elemento de superficie considerado de la gota. En la figura, se muestra el radio mínimo r₁ en el plano vertical.

Δp es la diferencia de presión a través de la superficie del líquido en este caso es la presión hidrostática correspondiente a la altura y

${\displaystyle \rho gy=\gamma \left(\frac{1}{r_1}+\frac{1}{r_2}\right)}$

Teniendo en cuenta que

${\displaystyle \begin{array}{l}\tan \theta =\frac{dy}{dx}\\ ds=r_{1}d\theta \\ dy=ds\sin \theta \end{array}}$

Obtenemos

${\displaystyle \begin{array}{l}dy=r_1\sin \theta ·d\theta \\ dy\left(\frac{\rho gy}{\gamma }-\frac{1}{r_2}\right)=\sin \theta ·d\theta \end{array}}$

Integramos. Supondremos que r₂ es constante

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{h}{\int }}dy\left(\frac{\rho gy}{\gamma }-\frac{1}{r_2}\right)}={\displaystyle \underset{0}{\overset{{\theta }_c}{\int }}\sin \theta ·d\theta }\\ \frac{1}{2}\frac{\rho g{h}^2}{\gamma }-\frac{h}{r_2}=1-\cos {\theta }_c\end{array}}$

Consideramos el caso de una gota cuyo radio de la base R es mucho mayor que la altura h, los radios de curvatura r₂>>r₁, el segundo término 1/r₂ en la ecuación de Young-Laplace es pequeño respecto del primero 1/r₁. En la expresión anterior, si el radio de curvatura r₂ es grande comparado con h

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{\rho g{h}^2}{\gamma }\approx 1-\cos {\theta }_c\\ \gamma =\frac{\rho g{h}^2}{2\left(1-\cos {\theta }_c\right)}\end{array}}$

Medido el ángulo de contacto θ_c y la altura h, determinamos la tensión superficial γ mediante una expresión simple. Al despreciar el término h/r₂, se produce una sobrevaloración de la tensión superficial γ

Referencias

F. Behroozi, P. S. Behroozi. Reliable determination of contact angle from the height and volume of sessile drops. Am. J. Phys. 87 (1) January 2019, pp. 28-32

Feredoon Behroozi, Hilliard K. Macomber, Jack A. Dostal, Cyrus H. Behroozi. The profile of a dew drop. Am. J. Phys. 64 (9) September 1996, pp. 1120-1125

F. Behroozi. Determination of contact angle from maximum height of enlarged drops on solid surface. Am. J. Phys. 80 (4) April 2012, pp. 284-288