El Gerris lacustris, el insecto zapatero, habita en lagos y estanques de los jardines, caminando sobre las aguas con total facilidad. Su tamaño oscila entre los dos y tres centímetros de longitud. Sobre su cabeza posee largas antenas y grandes ojos. También posee tres largos pares de patas, de las cuales, las cuatro traseras las utiliza para impulsarse y como timón, mientras que las dos delanteras, algo más cortas, las utiliza para atrapar a sus presas.

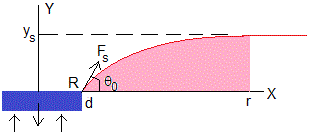
Consideremos un disco de radio R y espesor d cuya densidad ρ_d es mayor que la del agua 1000 kg/m³=1 g/cm³. Se coloca con mucho cuidado sobre la superficie del agua, observamos que se mantiene en equilibrio

La superficie plana y horizontal del agua se perturba por la presencia del disco en sus proximidades, que se hunde hasta una profundidad y_s por debajo de la superficie horizontal sin perturbar.

Dada la simetría cilíndrica del problema, establecemos el origen y los ejes: el eje Y vertical y el eje X en la dirección radial. La línea de color rojo, es el aspecto de la superficie del agua en las proximidades del disco, hasta una distancia r suficientemente grande a partir de la cual, se considera que la la superficie del agua es plana y horizontal.

Equilibrio del disco

El disco está en equelibrio bajo la acción de las fuerzas:

• El peso del disco, F_g=mg=ρ_d(πR²d)·g

• La fuerza que ejerce la presión del agua ρg(y_s+d) sobre la base inferior del disco

${\displaystyle F_p=\rho g\left(y_s+d\right)\pi R^2}$

• La componente vertical F_s·sinθ₀ de la fuerza que ejerce la tensión superficial F_s=γ(2πR)

La condición de equilibrio es

${\displaystyle \begin{array}{l}mg=\rho g\left(y_s+d\right)\pi R^2+2\pi \gamma R\sin {\theta }_0\\ \sin {\theta }_0=Rg\frac{{\rho }_{d}d-\rho \left(y_s+d\right)}{2\gamma }\end{array}}$

θ₀ es el ángulo que forma la tangente a superficie del agua en el bode del disco. Este ángulo deberá ser menor que el ángulo de contacto θ_c para que el disco no se hunda. Por ejemplo, el ángulo de contacto del agua con el aluminio es 65°. Este ángulo limita el peso del disco o su densidad

Forma de la superficie del agua

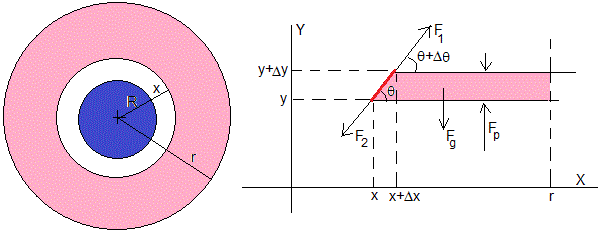
Vamos a estudiar el equilibrio de una sección horizontal de líquido, comprendida entre x>R y r, entre los planos horizontales que pasan por y e y+Δy, tal como se muestra en la figura. Las fuerzas sobre esta porción de fluido son:

• El peso

${\displaystyle F_g=\rho g\pi \left(r^2-x^2\right)\Delta y}$

• La fuerza que ejerce la presión del líquido

• La fuerza que ejerce la presión del fluido, sobre la superficie inferior de radios x (interior), r (exterior) y altura y

${\displaystyle F_{p1}=\rho g\left(y_s-y\right)\pi \left(r^2-x^2\right)}$

• La fuerza que ejerce la presión del fluido, sobre la superficie superior de radios x+Δx (interior), r (exterior) y altura y+Δy

${\displaystyle F_{p2}=\rho g\left(y_s-(y+\Delta y)\right)\pi \left(r^2-{\left(x+\Delta x\right)}^2\right)}$

ambas de sentido contrario. La diferencia, es una fuerza hacia arriba

${\displaystyle F_p=F_{p1}-F_{p2}\approx \pi \rho g\left(2x\left(y_s-y\right)\Delta x+\left(r^2-x^2\right)\Delta y\right)}$

• La fuerza que ejerce la tensión superficial

• F₂=γ(2πx), sobre la circunferencia de radio x, cuya dirección es tangente a la superficie. Su componente a lo largo del eje Y, es F₂sinθ

• F₁=γ(2πx+Δx), sobre la circunferencia de radio x+Δx. Su componente a lo largo del eje Y, es F₁sinθ+Δθ

La diferencia es una fuerza hacia arriba

${\displaystyle \begin{array}{l}{F}_s=F_1\sin \left(\theta +\Delta \theta \right)-F_2\sin \theta =2\pi \gamma (x+\Delta x)\sin \left(\theta +\Delta \theta \right)-2\pi \gamma x\sin \theta =\\ 2\pi \gamma (x+\Delta x)\left(\sin \theta +\cos \theta ·\Delta \theta \right)-2\pi \gamma x\sin \theta \approx \\ 2\pi \gamma \left(x\cos \theta ·\Delta \theta +\sin \theta ·\Delta x\right)\end{array}}$

La condición de equilibrio es, F_g=F_p+F_s

${\displaystyle \begin{array}{l}\rho g\pi \left(r^2-x^2\right)\Delta y=\pi \rho g\left(2x\left(y_s-y\right)\Delta x+\left(r^2-x^2\right)\Delta y\right)+2\pi \gamma \left(x\cos \theta ·\Delta \theta +\sin \theta ·\Delta x\right)\\ \rho gx\left(y_s-y\right)\Delta x+\gamma \left(x\cos \theta ·\Delta \theta +\sin \theta ·\Delta x\right)=0\\ \rho gx\left(y_s-y\right)\Delta x+\gamma \Delta \left(x\sin \theta \right)=0\end{array}}$

En el límite, cuando Δx→0

${\displaystyle \frac{\rho g}{\gamma }x\left(y_s-y\right)+\frac{d}{dx}\left(x\sin \theta \right)=0}$

Teniendo en cuenta que

${\displaystyle \tan \theta =\frac{dy}{dx},\sin \theta =\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}}$

Operando y simplificando llegamos a una ecuación diferencial de segundo orden

${\displaystyle \begin{array}{l}\frac{\rho g}{\gamma }x\left(y_s-y\right)+\frac{d}{dx}\left(x\frac{\frac{dy}{dx}}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}\right)=0\\ \frac{\rho g}{\gamma }x\left(y_s-y\right)+\frac{d}{dx}\left(x\frac{y\text{'}}{\sqrt{1+y{\text{'}}^2}}\right)=0\\ \frac{\rho g}{\gamma }x\left(y_s-y\right)+\frac{y\text{'}}{\sqrt{1+y{\text{'}}^2}}+x\frac{y\text{'}\text{'}\sqrt{1+y{\text{'}}^2}-\frac{y\text{'}y\text{'}\text{'}}{\sqrt{1+y{\text{'}}^2}}y\text{'}}{1+y{\text{'}}^2}=0\\ \frac{\rho g}{\gamma }x\left(y_s-y\right){\left(1+y{\text{'}}^2\right)}^{3/2}+y\text{'}\left(1+y{\text{'}}^2\right)+xy\text{'}\text{'}=0\end{array}}$

La forma de la superficie de líquido en la dirección radial, viene dada por la ecuación diferencial

${\displaystyle \frac{d^{2}y}{d{x}^2}=-\frac{\frac{dy}{dx}\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}{x}-\frac{\rho g}{\gamma }\left(y_s-y\right){\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}$

Resolveremos esta ecuación diferencial utilizando procedimientos numéricos con las siguientes condiciones iniciales:

• La posición inicial es x=R, y=0.
• La derivada primera en este punto vale (dy/dx)_R=tanθ₀. Donde θ₀ es el ángulo de equilibrio cuya expresión se ha deducido en el primer apartado

Sistema de unidades

Medimos las distancias en mm=10^-3 m, la densidad del líquido en unidades de 10³ kg/m³ y la tensión superficial en unidades de 10^-3 N/m

${\displaystyle \begin{array}{l}\frac{d^{2}y·{10}^{-3}}{d{x}^2·{10}^{-6}}=-\frac{\frac{dy}{dx}\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}{x·{10}^{-3}}-\frac{\rho ·{10}^{3}g}{\gamma ·{10}^{-3}}\left(y_s-y\right)·{10}^{-3}{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}\\ \frac{d^{2}y}{d{x}^2}=-\frac{\frac{dy}{dx}\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}{x}-9.8\frac{\rho }{\gamma }\left(y_s-y\right){\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}\end{array}}$

Para el agua ρ=1, γ=73

En este sistema de unidades el ángulo de equilibrio θ₀ se calcula mediante la fórmula

${\displaystyle \begin{array}{l}\sin {\theta }_0=R·{10}^{-3}g\frac{{\rho }_d·{10}^{3}d·{10}^{-3}-\rho ·{10}^3\left(y_s+d\right){10}^{-3}}{2\gamma ·{10}^{-3}}\\ \sin {\theta }_0=9.8\frac{{\rho }_{d}d-\rho \left(y_s+d\right)}{2\gamma }R\end{array}}$

Profundidad y_s del disco

El resultado más importante es la profundidad del disco, y_s relativo a la superficie plana y horizontal del agua sin perturbar, la altura y cuando x→∞

Sin embargo, y_s es un parámetro de la ecuación diferencial que no conocemos. Para calcularlo procederemos del siguiente modo

1. Establecemos el radio R, espesor d y densidad ρ_d del disco sobre la superficie del agua, ρ=1, γ=73
2. Calculamos el ángulo θ₀ de equilibrio del disco, estableciendo las condiciones iniciales: posición inicial y valor de la derivada primera
3. Damos un valor inicial al parámetro y_s
4. Resolvemos la ecuación diferencial, por procedimientos numéricos entre x=R y x=r, siendo r una distancia suficientemente grande al disco para considerar que la superficie del agua es aproximadamente plana y horizontal. En la práctica, tomaremos r=2R
5. Observamos el valor final de y para x=r, que diferirá del valor inicial de y_s.

Tenemos una ecuación transcedente y_s=g(y_s), cuya solución buscamos aplicando el procedimiento de Newton-Raphson. Dado que no conocemos la función f(x)=g(x)-x=0 de forma explícita ni su derivada, el procedimiento a aplicar es

${\displaystyle \begin{array}{l}{x}_{n+1}=x_n-\frac{f(x_n)}{\frac{f(x_n+\delta )-f(x_n)}{\delta }}\\ x_{n+1}=x_n-\frac{g(x_n)-x_n}{\frac{g(x_n+\delta )-g(x_n)}{\delta }-1}\end{array}}$

donde δ es una cantidad pequeña

El proceso de convergencia se termina en un número N de pasos o cuando se alcanza la precisión deseada

${\displaystyle \left|\frac{x_{n+1}-x_n}{x_{n+1}}\right|<\epsilon }$

Ejemplo

• Densidad del disco, ρ_d=2
• Tensión superficial del agua, γ=73
• Radio del disco, R=10
• Espesor del disco, d=1
• Establecemos el valor inicial de y_s=0.6

Aplicamos el procedimiento de Newton-Raphson hasta que se alcanza la precisión deseada o completa un número N de iteracciones

Representamos gráficamente la función y(x) desde x=R hasta x=r, que representa la forma de la superficie del agua, perturbada por el disco, en la dirección radial

rho_d=2; %densidad disco
gamma=73; %tensión superficial
R=10; %mm borde del disco
d=1; % mm, espesor del disco
r=2*R; %infinito!!

%procedimiento de Newton-Rapshon
y0=0.6; %valor inicial de ys
delta=0.0001;
N=20; %pasos
for i=1:N
    ys=y0;
    th_0=asin((d*rho_d-(ys+d))*9.8*R/(2*gamma));
    if(~isreal(th_0))
        disp('cambie el valor inicial')
        break;
    end
    f=@(t,x) [x(2); -x(2)*(1+x(2)^2)/t-9.8*(ys-x(1))*(1+x(2)^2)^(3/2)/gamma];
    [t,x]=ode45(f,[R,r],[0,tan(th_0)]);
    y1=x(end,1);
    ys=y0+delta;
    th_0=asin((d*rho_d-(ys+d))*9.8*R/(2*gamma));
    f=@(t,x) [x(2); -x(2)*(1+x(2)^2)/t-9.8*(ys-x(1))*(1+x(2)^2)^(3/2)/gamma];
    [t,x]=ode45(f,[R,r],[0,tan(th_0)]);
    y2=x(end,1);
    y2=y0-(y1-y0)/((y2-y1)/delta-1);
    if abs((y2-y0)/y2)<0.0001
        break;
    end
    y0=y2;
end
if(i==N)
    disp('No se alcanza la precisión deseada')
end

%gráficos
plot(t,x(:,1))
axis equal
grid on
xlabel('x')
ylabel('y')
title('Disco sobre el agua')

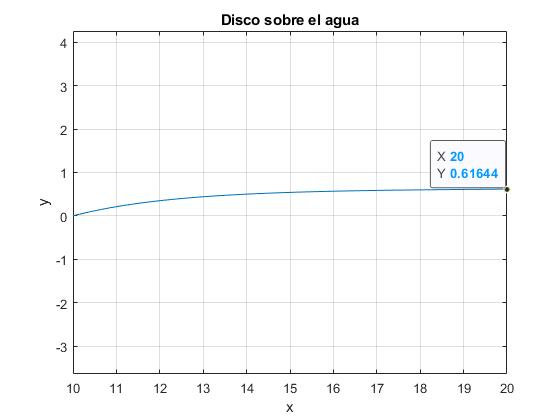
Observamos que la función y(x) crece desde cero, tendiendo hacia un valor constante cuando x se incrementa. El valor final de y_s es

>> x(end,1)
ans =    0.6164

No es fácil dar con el valor inicial de y_s. Por ejemplo, para los valores iniciales 0.5 y 0.7 la función crece o decrece y aparecen avisos en la ventana de comandos de que la ecuación diferencial no se puede resolver adecuadamente. Otras veces el ángulo θ₀ se hace un número complejo, que no es físicamente posible

Otro ejemplo tomado de la figura 2 del artículo mencionado en las referencias

• Densidad del disco, ρ_d=5
• Tensión superficial del agua, γ=73
• Radio del disco, R=10
• Espesor del disco, d=1
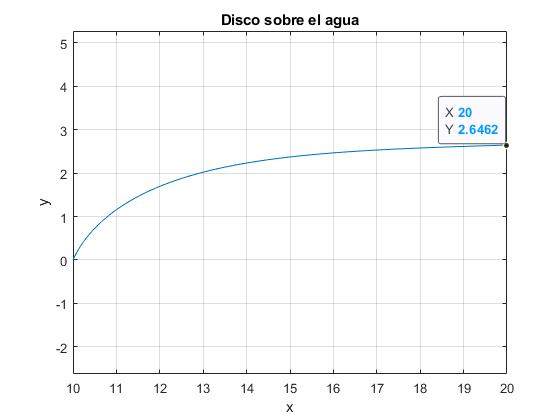
• Establecemos el valor inicial de y_s=2.62

rho_d=5; %densidad disco
gamma=73; %tensión superficial
R=10; %mm borde del disco
d=1; % mm, espesor del disco
r=2*R; %infinito!!

y0=2.62; %valor inicial de ys
....

Referencias

A Raymond Penner. Suspension of a disk on a surface of water. Am. J. Phys. 68 (6) June 2000, pp. 549-551