Verificación experimental de la función de distribución de las velocidades moleculares
Las moléculas de un gas escapan a través de un orificio practicado en el recipiente de un horno que está a cierta temperatura T. Mediante colimadores se consigue que solamente continúen su movimiento aquellas que tienen una determinada dirección. A continuación, pasan a través de un selector de velocidades que constan de dos discos iguales y paralelos, separados una distancia d, cada uno con una muesca que giran con la misma velocidad angular constante ω. Las muescas están desplazadas un ángulo θ.
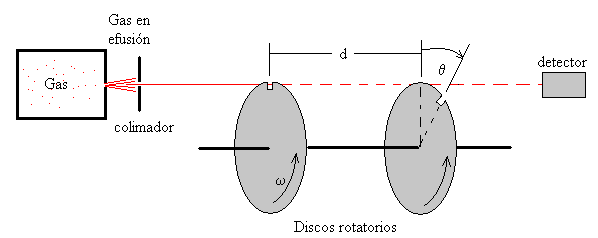
Solamente, pasan a través del selector aquellas moléculas cuya velocidad sea
Es decir, aquellas que saliendo a través de la muesca del primer disco, empleen el mismo tiempo en recorrer la distancia d, t=d/v, que el segundo disco en girar un ángulo θ, t= θ/ω, para que su muesca se sitúe en la dirección del haz.
En realidad, como las muescas tienen un ancho finito, las moléculas que llegan al detector tienen velocidades comprendidas en cierto intervalo Δv, alrededor de la velocidad v. Cambiando el ángulo entre las muescas θ, o la velocidad angular de rotación ω, seleccionamos otra velocidad v del haz de moléculas.
Este es el procedimiento que se describe en varios libros de texto. Existen otros muchos métodos, entre los que cabe destacar el siguiente:
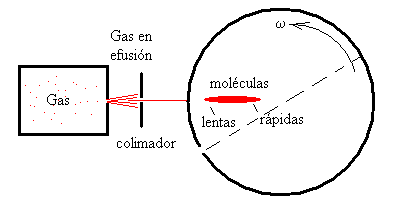
Las moléculas que escapan a través de un orificio practicado en la pared del horno calentado a temperatura T, pasan por un colimador. Una pequeña parte de estas moléculas que entran en el tambor a través de un orificio O. Las moléculas que tienen distintas velocidades, continúan su movimiento rectilíneo hasta que se encuentran con la pared interna del tambor que está revestida con una lámina de vidrio.
Las moléculas más lentas, tardan más tiempo en depositarse en el revestimientote vidrio, el ángulo girado por el tambor será mucho mayor. La distribución espacial de las moléculas a lo largo del revestimiento está relacionada con sus velocidades como veremos a continuación.
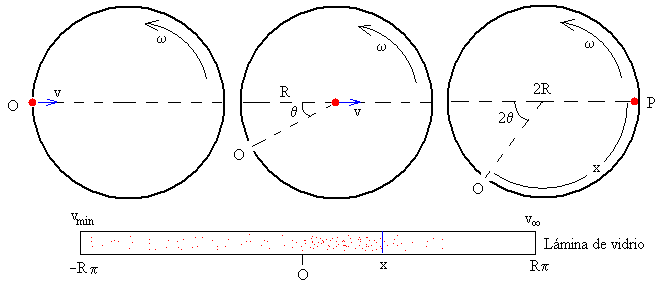
Calculemos el punto P de impacto de una molécula que lleva una velocidad v en el revestimiento de vidrio, sabiendo que el radio del tambor es R, y su velocidad angular de rotación es ω. Como vemos en los tres dibujos, en el tiempo t que tarda la molécula en recorrer el diámetro 2R del tambor, t=2R/v, el orificio O del tambor ha girado un ángulo 2θ=ω·t. El punto P de impacto de la molécula en el revestimiento de vidrio, se encuentra a una distancia x del orificio, que es la longitud del arco de una circunferencia de radio R y ángulo π-2θ.
Las moléculas muy rápidas tenderán a concentrarse en la posición opuesta al orificio. x=Rπ. Mientras que las muy lentas llegarán al revestimiento, después de que el tambor haya dado varias vueltas. Las moléculas que tardan en recorrer el diámetro del tambor el mismo tiempo que éste tarda en dar una vuelta completa, se situarán en la posición x=-Rπ. Su velocidad será
Un dispositivo fijado al tambor elimina las moléculas cuya velocidad es inferior a vmín. De este modo, evitamos que en la misma posición del tambor se encuentren moléculas rápidas y lentas.
En la posición opuesta x=Rπ se situarán aquellas moléculas cuya velocidad sea teóricamente infinita.
Se han diseñado dos programas interactivos para mostrar el funcionamiento de este dispositivo que nos permite comprobar la ley de distribución de velocidades.
- El primero, se basa en un modelo de gas ideal bidimensional.
- El segundo, en la efusión de un gas.
Actividades
Se introduce
-
La temperatura, en el intervalo 5-40 unidades actuando en la barra de desplazamiento titulada Temperatura.
-
La masa de las moléculas, en el intervalo 1-5 unidades, actuando en la barra de desplazamiento titulada Masa.
-
La velocidad angular de rotación del tambor, en el intervalo 1-5 unidades, actuando en la barra de desplazamiento titulada Velocidad angular
-
El radio del tambor se ha fijado en R=20 unidades
Se pulsa el botón Nuevo y después ►
El applet está dividido en tres zonas:
-
En la primera, se muestra las moléculas del gas ideal bidimensional, en el interior de un recipiente rectangular, con un orificio por donde salen las moléculas.
-
En la segunda, un tambor giratorio, con un orificio por donde entra una pequeña porción de las moléculas del haz cuando pasa enfrente del orificio del recipiente.
-
Conocida la relación entre la posición x de una molécula en el revestimiento de vidrio del tambor y su velocidad v, y el número de moléculas que se depositan en cada intervalo Δx, podemos trazar un diagrama de barras, como el que se muestra en la parte derecha del applet.
Las moléculas se mueven a lo largo del diámetro horizontal del tambor giratorio, hasta que chocan con su superficie interior revestida de una lámina de vidrio.
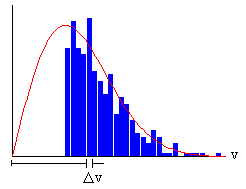
La altura de cada barra, es proporcional al número de moléculas cuya velocidad está comprendida entre v, y v+Δv. La anchura del intervalo es de de Δv=0.5 unidades.
Como podemos apreciar, el diagrama de barras se aproxima a la función de distribución de las velocidades moleculares cuando el número de moléculas es grande.
Actividades
Se introduce
-
Se elige una sustancia metálica el control de selección titulado Sustancia.
-
La temperatura T del horno (en grados K), en el control titulado Temperatura. La mayor parte de los metales se convierten en vapor a muy altas temperaturas del orden de 2000º C o superiores a la presión atmosférica. En la simulación consideraremos que el metal puede estar en estado de vapor a la temperatura que introduzcamos
-
La velocidad angular ω de rotación del tambor (en rad/s), actuando en la barra de desplazamiento, o introduciendo su valor en el control titulado Velocidad angular.
-
El radio del tambor se ha fijado en el valor R=1 m
Se pulsa en el botón titulado Nuevo.
Se representa la función de distribución de velocidades de las moléculas del haz que sale a través de un orificio, perpendicularmente (eje Z) a la pared de un horno que contiene el vapor del metal seleccionado, y que se deducirá más adelante.
En la gráfica se han marcado tres valores.
-
El valor vmín=Rω/π, que es la mínima velocidad que detecta este dispositivo
-
El valor de la velocidad para el cual la función de distribución presenta un máximo, que como el lector fácilmente deducirá es
-
La velocidad vmáx a partir del cual la función de distribución se hace aproximadamente cero.

Estos tres valores se proyectan en la lámina de vidrio que cubre la pared interna del tambor (en la parte inferior), y que se señalan mediante líneas verticales de color azul. La relación de transformación, que hemos deducido anteriormente, es
Las moléculas con velocidad vmín=Rω/π se sitúan en la posición x=-Rπ, extremo izquierdo de la lámina. En el lado opuesto, se situarán las moléculas que lleven una velocidad teóricamente infinita v∞.
Las otras dos velocidades se sitúan en las posiciones indicadas por las rayas verticales de color azul. En el centro de la lámina, un círculo de color negro, señala el orificio que se ha hecho en el tambor y que se toma como origen de las posiciones de las moléculas en la lámina.
En la práctica real, las posiciones de las moléculas en la lámina de vidrio se transforman en velocidades mediante la relación de transformación inversa
La intensidad del color, o la medida de la transparencia de la lámina de vidrio, nos proporciona del número de moléculas en cada intervalo Δx alrededor de posición x. En la experiencia simulada, el número de moléculas que se depositan en la lámina en una posición x dada, determina la intensidad del color rojo, tal como podemos apreciar en la figura.
La habilidad del “experimentador” estará en seleccionar la velocidad angular del tambor, de modo que la distribución de las velocidades de las moléculas del haz se pueda “medir” lo más cómodamente posible, para la sustancia elegida y temperatura del horno.
Datos
| Vapor de la sustancia | Masa atómica (g) |
| Cobre (Cu) | 63.54 |
| Plata (Ag) | 107.87 |
| Plomo (Pb) | 207.19 |
| Wolframio (W) | 183.85 |
| Aluminio (Al) | 26.98 |
Fuente: Alonso, Finn. Física. Fundamentos cuánticos y estadísticos, Edt. Fondo Educativo Interamericano (1971)
- Constante de Boltzmann k= 1.3805·10-23 J/K
- Número de Avogadro NA=6.0225·1023 mol-1
Ejemplo:
Tenemos un horno calentado a 1000 K, con vapor de Wolframio. Seleccionamos la velocidad angular de rotación ω=220 rad/s.
La velocidad que corresponde al máximo de la función de distribución es
La posición x de los átomos que llevan esta velocidad en la lámina de vidrio es
La posición marcada por una línea vertical de color azul a la derecha del origen.
Aplicamos la relación inversa. La velocidad de los átomos que se han depositado en la posición x=-2 es
La velocidad mínima x=-Rπ los átomos que se depositan en la lámina de vidrio es
Gas ideal bidimensional
En estasección, se comentan los pasos esenciales para crear la simulación del experimento que nos permite comprobar la fórmula de la distribución de las velocidades moleculares. Se emplea un modelo de gas bidimensional
Volvemos sobre la distribución de las velocidades moleculares. El número de moléculas cuya velocidad está comprendida entre y o bien, entre vx y vx+dvx, vy y vy+dvy de acuerdo a la ley de Boltzmann es
donde c es una constante a determinar sabiendo que el número total de moléculas es N.
Se efectúa una integral doble entre los límites -∞ y +∞ , teniendo en cuenta el resultado de la integral
El resultado es
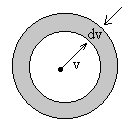
En el espacio de velocidades del gas bidimensional, el elemento de área, es el área del anillo comprendido entre las circunferencias de radio v y v+dv. dv=2π vdv, tal como se ve en la figura
El número de partículas cuyo módulo de la velocidad está comprendida entre v y v+dv es
donde T es la temperatura relacionada con la velocidad media <v> de las N moléculas del gas ideal bidimensional.
La velocidad media <v> de las moléculas del gas bidimensional está relacionada con su temperatura T.
Para deducir estas expresiones, se han empleado el resultado de las integrales
Para generar la distribución de las velocidades de las moléculas de un gas ideal bidimensional, se emplean los métodos de Montecarlo.
Se genera números aleatorios γ, uniformemente distribuidos en el intervalo [0, 1), para cada número γ se obtiene la velocidad de una molécula de acuerdo con la siguiente fórmula
La ventaja de utilizar este modelo, es que la integral es inmediata y se despeja fácilmente v.
Finalmente, se sitúa cada molécula en el tambor, en la posición dada por la relación de transformación

