Choque de una molécula contra un émbolo móvil

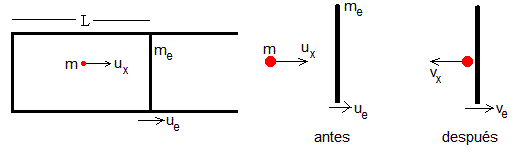
Una partícula de masa m y velocidad u_x choca elásticamente con un émbolo de masa m_e que se mueve con velocidad u_e

Conservación del momento lineal y la igualdad de la energía cinética antes y después del choque

${\displaystyle \begin{array}{l}m{u}_x+m_e{u}_e=m{v}_x+m_e{v}_e\hfill \\ \frac{1}{2}m{u}_x^2+\frac{1}{2}{m}_e{u}_e^2=\frac{1}{2}m{v}_x^2+\frac{1}{2}{m}_e{v}_e^2\hfill \end{array}}$

Escribimos las dos ecuaciones en la forma equivalente

${\displaystyle \begin{array}{l}m\left(u_x-v_x\right)=m_e\left(v_e-u_e\right)\\ m\left(u_x-v_x\right)\left(u_x+v_x\right)=m_e\left(v_e-u_e\right)\left(v_e+u_e\right)\end{array}}$

Despejando las incógnitas

${\displaystyle v_x=\frac{2u_e-\left(1-\frac{m}{m_e}\right)u_x}{1+\frac{m}{m_e}},v_e=\frac{2\frac{m}{m_e}{u}_x+\left(1-\frac{m}{m_e}\right)u_e}{1+\frac{m}{m_e}}}$

Como la masa m_e del émbolo es muy grande comparado con masa m de la partícula

${\displaystyle v_x\approx 2u_e-u_x,v_e\approx u_e}$

El émbolo no cambia apenas de velocidad como resultado del choque con las moléculas ya que su masa m_e es muy grande comparada con la masa m de una molécula. Sin embargo, como el número de choques es muy grande, para que el émbolo se mantenga con velocidad constante es necesario ejercer una fuerza.

Supongamos que el gas consiste en N partículas contenidas en el volumen cilíndrico V=AL, de longitud L y sección A, tal como se muestra en la figura. El émbolo se mueve con velocidad u_e. El número de colisiones de las moléculas con velocidad u_x≥u_e con el émbolo en el tiempo Δt es

${\displaystyle A\frac{N}{V}\left(u_x-u_e\right)\Delta t}$

Las moléculas con velocidad u_x<u_e no alcanzan el émbolo

La variación de energía cinética que experimenta el gas en cada choque con el émbolo es

${\displaystyle \Delta \epsilon =\frac{1}{2}m{v}_x^2-\frac{1}{2}m{u}_x^2\approx \frac{1}{2}m{\left(2u_e-u_x\right)}^2-\frac{1}{2}m{u}_x^2=-2m{u}_e\left(u_x-u_e\right)}$

La variación de energía que experimenta el gas en la unidad de tiempo debido a las moléculas con velocidad u_x

${\displaystyle \frac{\Delta {\epsilon }_T}{\Delta t}=-2A\frac{N}{V}m{u}_e{\left(u_x-u_e\right)}^2}$

En la página titulada La ley de distribución de las velocidades moleculares, calculamos el número de moléculas cuya componente X de la velocidad está comprendida entre u_x, u_x+du_x independientemente de los valores de las otras dos componentes, integrando respecto de u_y y u_z entre los límites -∞ y +∞.

${\displaystyle \begin{array}{l}d{n}_x=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\left\{{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{m{u}_y^2}{2kT}\right)}d{u}_y·{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{m{u}_z^2}{2kT}\right)}d{u}_z\right\}\exp \left(-\frac{m{u}_x^2}{2kT}\right)d{u}_x=\\ N{\left(\frac{m}{2\pi kT}\right)}^{1/2}\exp \left(-\frac{m{u}_x^2}{2kT}\right)d{u}_x\end{array}}$

Relación entre temperatura T y volumen V del gas

La variación de energía que experimenta el gas en la unidad de tiempo debido a todas las moléculas con velocidad u_x≥u_e es

${\displaystyle \frac{dU}{dt}=-{\displaystyle \underset{u_e}{\overset{\infty }{\int }}2A\frac{N}{V}m{u}_e{\left(u_x-u_e\right)}^2{\left(\frac{m}{2\pi kT}\right)}^{1/2}\exp \left(-\frac{m{u}_x^2}{2kT}\right)d{u}_x}}$

Es muy útil escribir esta ecuación en términos de dos parámetros adimensionales α y β

${\displaystyle u_x=\alpha \sqrt{\frac{3kT}{m},}{u}_e=\beta \sqrt{\frac{3kT}{m},}}$

El término que multiplica a ambos parámetros es la velocidad v_rms

${\displaystyle \frac{dU}{dt}=-A\frac{N}{V}\sqrt{\frac{6}{\pi }}{v}_{rms}^{3}m\beta {\displaystyle \underset{\beta }{\overset{\infty }{\int }}{\left(\alpha -\beta \right)}^2\exp \left(-\frac{3}{2}{\alpha }^2\right)d\alpha }}$

Relacionamos el cambio de volumen dV con el intervalo de tiempo dt sabiendo que el émbolo se mueve con velocidad constante u_e

${\displaystyle \begin{array}{l}V=A\left(x_0+u_{e}t\right)\\ dV=A{u}_{e}dt=A\beta v_{rms}dt\end{array}}$

x₀ es la posición inicial del émbolo. Por otra parte, el producto mN es la masa de las moléculas del gas que es el producto del número de moles n por el peso molecular M

${\displaystyle \frac{dU}{dV}=-\frac{nM}{V}\sqrt{\frac{6}{\pi }}{v}_{rms}^2{\displaystyle \underset{\beta }{\overset{\infty }{\int }}{\left(\alpha -\beta \right)}^2\exp \left(-\frac{3}{2}{\alpha }^2\right)d\alpha }}$

Aunque el gas no está en equilibrio, supondremos que es válida la relación dU=n·c_vdT. Su justificación se explica en el primer artículo citado en las referencias

Teniendo en cuenta que N_Ak=R. N_A=6.0225·10²³ mol^-1 es el número de Avogadro y R=8.3143 J/(K·mol) es la constante de los gases. Por otra parte, el peso molecular M=N_A·m, siendo m la masa de una molécula. La expresión anterior nos proporciona una relación entre el volumen y la temperatura del gas

${\displaystyle \begin{array}{l}\frac{n{c}_{v}dT}{dV}=-\frac{nM}{V}\sqrt{\frac{6}{\pi }}\frac{3kT}{m}{\displaystyle \underset{\beta }{\overset{\infty }{\int }}{\left(\alpha -\beta \right)}^2\exp \left(-\frac{3}{2}{\alpha }^2\right)d\alpha }\\ \frac{dT}{T}=-\frac{dV}{V}\frac{R}{c_v}3\sqrt{\frac{6}{\pi }}{\displaystyle \underset{\beta }{\overset{\infty }{\int }}{\left(\alpha -\beta \right)}^2\exp \left(-\frac{3}{2}{\alpha }^2\right)d\alpha }\\ \frac{dT}{T}=-r\frac{R}{c_v}\frac{dV}{V}\end{array}}$

Integramos la ecuación diferencial, sabiendo que la temperatura inicial es T₀ y la final T. El volumen inicial V₀ y el final V

${\displaystyle \frac{T}{T_0}={\left(\frac{V_0}{V}\right)}^{r\frac{R}{c_v}}}$

El parámetro r

En general, el parámetro r se ha de evaluar numéricamente, dado el valor de β o de la velocidad del émbolo u_e

${\displaystyle r=3\sqrt{\frac{6}{\pi }}{\displaystyle \underset{\beta }{\overset{\infty }{\int }}{\left(\alpha -\beta \right)}^2\exp \left(-\frac{3}{2}{\alpha }^2\right)d\alpha }}$

Cuando la velocidad del émbolo es muy pequeña u_e→0, entonces β→0. Utilizando el valor de la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp (-a{x}^2)dx}=\frac{1}{4}\sqrt{\frac{\pi }{a^3}}}$

>> syms x;
>> syms a positive
>> int('x^2*exp(-a*x^2)',x,0,inf)
ans =pi^(1/2)/(4*a^(3/2))

Obtenemos r=1, que corresponde a una transformación adiabática

Para β=1, la velocidad del émbolo u_e iguala a la velocidad media de las moléculas v_rms, el resultado de r es próximo a cero, ya que una gran parte de las moléculas del gas tiene una velocidad u_x más pequeña que el émbolo u_e

beta=1;
f=@(x) ((x-beta).^2).*exp(-3*x.^2/2);
r=3*sqrt(6/pi)*integral(f,beta,inf);
disp(r)

    0.0247

Calculamos y representamos r para algunos valores de β en el intervalo [0,1]

hold on
for beta=0:0.1:1
    f=@(x) ((x-beta).^2).*exp(-3*x.^2/2);
    r=3*sqrt(6/pi)*integral(f,beta,inf);
    plot(beta,r,'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
end
hold off
grid on
xlabel('\beta')
ylabel('r')
title('valores de r')

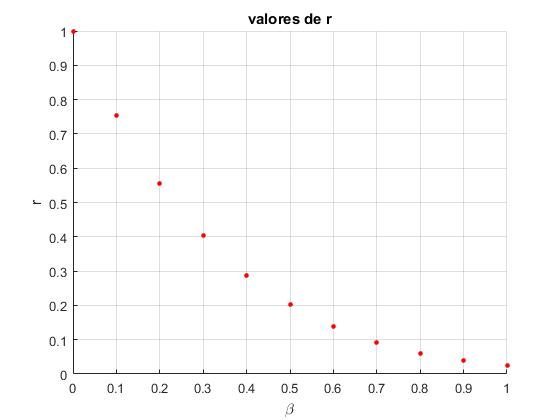
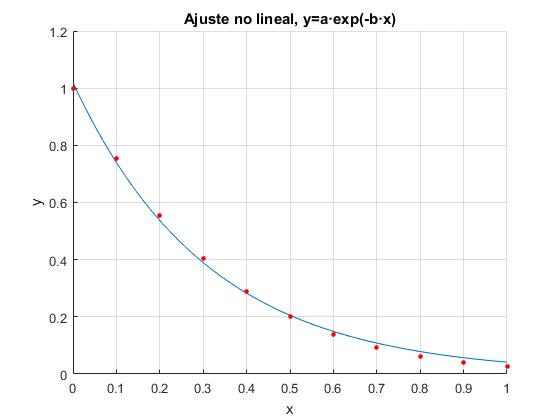
Ajustamos estos datos a una exponencial decreciente, y=a·exp(-b·x)

i=1;
x=0:0.1:1;
y=zeros(1,length(x));
for beta=x
    f1=@(x) ((x-beta).^2).*exp(-3*x.^2/2);
    y(i)=3*sqrt(6/pi)*integral(f1,beta,inf);
    i=i+1;
end
f=@(a,x) a(1)*exp(-a(2)*x);      
error=@(a) sum((y-f(a,x)).^2);
a0=[1,3.2];  %valor inicial
af=fminsearch(error,a0);
g=@(x) f(af,x);
hold on
fplot(g,[x(1),x(end)])
plot(x,y,'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
title('Ajuste no lineal, y=a·exp(-b·x)')
xlabel('x')
ylabel('y')
grid on

af =    1.0191    3.2041

El parámetro a=1 y b=3.2. Podríamos utilizar esta función exponencial para calcular el valor de r para un valor dado de β, en vez de realizar la integración numérica

Referencias

E N Miranda What lies between a free adiabatic expansion and a quasi-static one? . Eur. J. Phys. 29 (2008), pp. 937-943