Gas ideal unidimensional

El medio en el que se mueve el objeto es un gas ideal unidimensional, el eje X.

De acuerdo con la ley de Boltzmann el número de moléculas cuya velocidad está comprendida entre v y v+dv es

${\displaystyle dn=c·\exp \left(\frac{-m{v}^2}{2kT}\right)dv}$

La constante c de proporcionalidad se determina teniendo en cuenta que las N partículas tienen sus velocidades comprendidas entre -∞ y +∞

${\displaystyle N=c·{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(\frac{-m{v}^2}{2kT}\right)dv}}$

Calculamos la constante c, a partir del resultado de la integral

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}=\frac{1}{2}\sqrt{\frac{\pi }{\alpha }}\\ dn=N\sqrt{\frac{m}{2\pi kT}}\exp \left(-\frac{m{v}^2}{2kT}\right)dv\end{array}}$

>> syms x;
>> syms a positive
>> int(exp(-a*x^2),x,0,inf) 
ans =pi^(1/2)/(2*a^(1/2))

Velocidad cuadrática media

El número de moléculas cuyo módulo de la velocidad está comprendida entre v y v+dv es

${\displaystyle dn=C·\exp \left(\frac{-m{v}^2}{2kT}\right)dv}$

La constante C de proporcionalidad se calcula teniendo en cuenta que las N partículas tienen los módulos de sus velocidades comprendidas entre 0 y +∞

${\displaystyle \begin{array}{l}N=C·{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(\frac{-m{v}^2}{2kT}\right)dv}\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}=\frac{1}{2}\sqrt{\frac{\pi }{\alpha }}\\ dn=2N\sqrt{\frac{m}{2\pi kT}}\exp \left(-\frac{m{v}^2}{2kT}\right)dv\end{array}}$

La velocidad cuadrática media de las moléculas del gas unidimensional es

${\displaystyle <v^2>={\displaystyle \underset{0}{\overset{\infty }{\int }}{v}^{2}dn}=2N\sqrt{\frac{m}{2\pi kT}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{v}^2\exp \left(-\frac{m{v}^2}{2kT}\right)dv}}$

Teniendo en cuenta el resultado de la integral

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp (-\alpha x^2)dx}=\frac{1}{4}\sqrt{\frac{\pi }{{\alpha }^3}}\\ <v^2>=\frac{kT}{m}\end{array}}$

>> syms x;
>> syms a positive
>> int(x^2*exp(-a*x^2),x,0,inf) 
ans =pi^(1/2)/(4*a^(3/2))

Denominamos V_T a la raíz cuadrada de la velocidad cuadrática media

${\displaystyle V_T=\sqrt{<v^2>}=\sqrt{\frac{kT}{m}}}$

La función de distribución de las moléculas del gas ideal es decir, el número de moléculas cuya velocidad está comprendida entre v y v+dv se expresa

${\displaystyle dn=\frac{N}{V_T}\sqrt{\frac{1}{2\pi }}\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}$

Choque entre el cuerpo y una partícula del medio

Supongamos dos partículas que se mueven a lo largo del eje X.

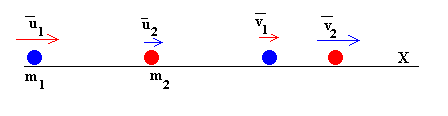
Una partícula de masa m₁ que lleva una velocidad u₁ choca contra otra partícula de masa m₂ que lleva una velocidad u₂.

La conservación del momento lineal se escribe

m₁u₁+m₂u₂=m₁v₁+m₂v₂

De la definición del coeficiente de restitución e

-e(u₁-u₂)=v₁-v₂

Despejando las velocidades después del choque v₁ y v₂

${\displaystyle v_1=\frac{(m_1-m_{2}e)u_1+m_2(1+e)u_2}{m_1+m_2}{v}_2=\frac{(m_2-m_{1}e)u_2+m_1(1+e)u_1}{m_1+m_2}}$

La variación del momento lineal de la segunda partícula es

${\displaystyle \Delta p_2=m_2{v}_2-m_2{u}_2=\frac{m_1{m}_2}{m_1+m_2}(1+e)(u_1-u_2)}$

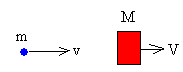
Consideremos un cuerpo de masa m₂=M que lleva una velocidad u₂=V. Una partícula del medio de masa m₁=m que lleva una velocidad u₁=v choca con el cuerpo. Supongamos que la masa del cuerpo M es mucho mayor que la masa de las moléculas del gas m. La velocidad del cuerpo V cambiará muy poco en un choque, la variación de su momento lineal será aproximadamente

${\displaystyle \Delta p\approx m(1+e)(v-V)}$

La fuerza de rozamiento

La velocidad inicial del cuerpo  de masa M es V₀, al cabo de un cierto tiempo t, su velocidad habrá disminuido a V, debido a los choques con las moléculas del gas.

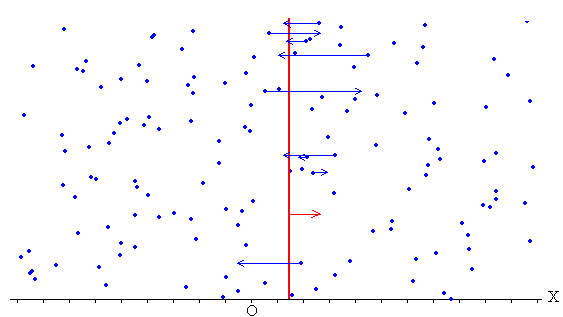
En la figura vemos que en el intervalo de tiempo Δt chocarán con el cuerpo (línea gruesa de color rojo) dos partículas (puntos de color azul) del gas situado en la parte izquierda y siete partículas del lado derecho. La longitud de la flecha es proporcional a la velocidad de la partícula.

En el intervalo de tiempo comprendido entre t y t+dt:

• El cuerpo chocará con las moléculas provenientes de la parte izquierda siempre que su velocidad v sea mayor que la velocidad V del cuerpo y estén a una distancia menor que (v-V)dt.

El número de tales moléculas es

${\displaystyle d{n}_L=\rho (v-V)dt·\frac{dn}{N}}$

Siendo ρ es la densidad de partículas y dn/N la probabilidad de que una molécula lleve una velocidad comprendida en el intervalo entre v y v+dv

El cuerpo incrementa su momento lineal debido a los choques con las moléculas de la parte izquierda dn_L cuyas velocidades están el intervalo (v, v+dv)

${\displaystyle \begin{array}{l}d{P}_L=\Delta p·d{n}_L\\ \frac{d{P}_L}{dt}=m(1+e)(v-V)\rho \frac{dn}{N}·(v-V)\end{array}}$

Integrando sobre todas las velocidades v>V calculamos la fuerza efectiva que ejercen las moléculas de la parte izquierda sobre el cuerpo

${\displaystyle F_L={\displaystyle \underset{V}{\overset{\infty }{\int }}\rho m(1+e){(v-V)}^2\frac{1}{V_T}\sqrt{\frac{1}{2\pi }}\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}}$

• El cuerpo chocará con las moléculas provenientes de la parte derecha siempre que su velocidad v sea menor que la velocidad V del cuerpo y estén a una distancia menor que (V-v)dt.

El número de tales moléculas es

${\displaystyle d{n}_R=\rho (V-v)dt·\frac{dn}{N}}$

El cuerpo cambia su momento lineal debido a los choques con las moléculas de la parte derecha dn_R cuyas velocidades están el intervalo (v, v+dv)

${\displaystyle \begin{array}{l}d{P}_R=\Delta p·d{n}_R\\ \frac{d{P}_R}{dt}=m(1+e)(v-V)\rho \frac{dn}{N}·(V-v)\end{array}}$

Integrando sobre todas las velocidades v<V calculamos la fuerza efectiva que ejercen las moléculas de la parte derecha sobre el cuerpo

${\displaystyle F_R=-{\displaystyle \underset{-\infty }{\overset{V}{\int }}\rho m(1+e){(V-v)}^2\frac{1}{V_T}\sqrt{\frac{1}{2\pi }}\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}}$

La fuerza total sobre el cuerpo será

$$\begin{gathered} {\displaystyle F=F_L+F_R=-\rho m(1+e)\frac{1}{V_T}\sqrt{\frac{1}{2\pi }}\left\{{\displaystyle \underset{-\infty }{\overset{V}{\int }}{(V-v)}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}- \\ {\displaystyle \underset{V}{\overset{\infty }{\int }}{(v-V)}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}\right\}} \end{gathered}$$

Calculamos la diferencia de las dos integrales

$$\begin{gathered} {\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{V}{\int }}{\left(V-v\right)}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}-{\displaystyle \underset{V}{\overset{\infty }{\int }}{\left(v-V\right)}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}=\\ {\displaystyle \underset{-\infty }{\overset{0}{\int }}{(v-V)}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}-{\displaystyle \underset{0}{\overset{\infty }{\int }}{(v-V)}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}+ \\ 2{\displaystyle \underset{0}{\overset{V}{\int }}{(v-V)}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}=\\ V^2{\displaystyle \underset{-\infty }{\overset{0}{\int }}\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}-2V{\displaystyle \underset{-\infty }{\overset{0}{\int }}v\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}+{\displaystyle \underset{-\infty }{\overset{0}{\int }}{v}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}\\ -V^2{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}+2V{\displaystyle \underset{0}{\overset{\infty }{\int }}v\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}-{\displaystyle \underset{0}{\overset{\infty }{\int }}{v}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}\\ +2V^2{\displaystyle \underset{0}{\overset{V}{\int }}\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}-4V{\displaystyle \underset{0}{\overset{V}{\int }}v\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}+2{\displaystyle \underset{0}{\overset{V}{\int }}{v}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}\end{array}} \end{gathered}$$

Las integrales parciales valen

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{0}{\int }}v\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}={-V_T^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)|}_{-\infty }^0=-V_T^2\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}v\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}={-V_T^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)|}_0^{\infty }=V_T^2\\ {\displaystyle \underset{0}{\overset{V}{\int }}v\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}={-V_T^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)|}_0^V=-V_T^2\exp \left(-\frac{1}{2}\frac{V^2}{V_T^2}\right)+V_T^2\\ {\displaystyle \underset{0}{\overset{V}{\int }}\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}=V_T\sqrt{\frac{\pi }{2}}\text{erf}\left(\frac{V}{\sqrt{2}{V}_T}\right)\\ {\displaystyle \underset{0}{\overset{V}{\int }}{v}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}=-V{V}_T^2\exp \left(-\frac{1}{2}\frac{V^2}{V_T^2}\right)+V_T^3\sqrt{\frac{\pi }{2}}\text{erf}\left(\frac{V}{\sqrt{2}{V}_T}\right)\end{array}}$

donde la función error se define

${\displaystyle \text{erf(}t\text{)=}\frac{2}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-t^2)dt}}$

El resultado final de la diferencia de las dos integrales es

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{V}{\int }}{(V-v)}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}-{\displaystyle \underset{V}{\overset{\infty }{\int }}{(v-V)}^2\exp \left(-\frac{1}{2}\frac{v^2}{V_T^2}\right)dv}=\\ 2V^2{V}_T\sqrt{\frac{\pi }{2}}\text{erf}\left(\frac{V}{\sqrt{2}{V}_T}\right)+2V{V}_T^2\exp \left(-\frac{1}{2}\frac{V^2}{V_T^2}\right)+2V_T^3\sqrt{\frac{\pi }{2}}\text{erf}\left(\frac{V}{\sqrt{2}{V}_T}\right)\end{array}}$

El valor de la fuerza sobre el cuerpo es

${\displaystyle F=-\rho m(1+e)V_T^2\left\{\left(\frac{V^2}{V_T^2}+1\right)\text{erf}\left(\frac{V}{\sqrt{2}{V}_T}\right)+\sqrt{\frac{2}{\pi }}\frac{V}{V_T}\exp \left(-\frac{1}{2}\frac{V^2}{V_T^2}\right)\right\}}$

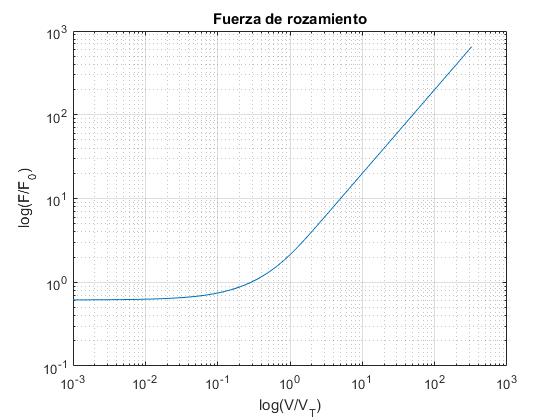
La representación de la fuerza de rozamiento F en función de la velocidad V del cuerpo, en una gráfica doblemente logarítmica, consiste básicamente en dos líneas rectas con pendientes de uno y dos, respectivamente, y una región de transición alrededor de V=V_T.

f=@(x) (x.^2+1).*erf(x/sqrt(2))+sqrt(2/pi)*x.*exp(-x.^2/2);
x=logspace(-3,3);
loglog(x,log(f(exp(x))))
xlabel('log(V/V_T)')
ylabel('log(F/F_0)')
title ('Fuerza de rozamiento')
grid on

Aproximaciones

• Cuando V<<V_T

${\displaystyle \begin{array}{l}t\to 0\text{erf(}t\text{)}\approx \frac{2}{\sqrt{\pi }}t\\ V<<V_T\text{erf}\left(\frac{V}{\sqrt{2}{V}_T}\right)\approx \frac{2}{\sqrt{\pi }}\frac{V}{\sqrt{2}{V}_T}\\ V<<V_T\exp \left(-\frac{1}{2}\frac{V^2}{V_T^2}\right)\approx 1\\ F\approx -\rho m(1+e)V_T^2\left\{\frac{2}{\sqrt{\pi }}\frac{V}{\sqrt{2}{V}_T}+\sqrt{\frac{2}{\pi }}\frac{V}{V_T}\right\}=-2\rho m(1+e)V_T\sqrt{\frac{2}{\pi }}V\end{array}}$

La fuerza de rozamiento es proporcional a la velocidad V del cuerpo

• Cuando V>>V_T

${\displaystyle \begin{array}{l}V>>V_T\text{erf}\left(\frac{V}{\sqrt{2}{V}_T}\right)\approx 1\\ V>>V_T\exp \left(-\frac{1}{2}\frac{V^2}{V_T^2}\right)\approx 0\\ F\approx -\rho m(1+e)V_T^2\left\{\frac{V^2}{V_T^2}\right\}=-\rho m(1+e)V^2\end{array}}$

La fuerza de rozamiento es proporcional al cuadrado de la velocidad V del cuerpo

Ecuaciones del movimiento

Cuando un cuerpo se mueve bajo la única acción de la fuerza de rozamiento F, la ecuación del movimiento es

${\displaystyle M\frac{dV}{dt}=F}$

• Si la velocidad inicial del cuerpo V₀<V_T la fuerza de rozamiento es proporcional a la velocidad.

${\displaystyle \begin{array}{l}\frac{dV}{dt}=-\frac{\rho m(1+e)}{M}2V_T\sqrt{\frac{2}{\pi }}V\\ {\displaystyle \underset{V_0}{\overset{V}{\int }}\frac{dV}{V}}=-\frac{\rho m(1+e)}{M}2V_T\sqrt{\frac{2}{\pi }}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ V=V_0\exp \left(-k·2V_T\sqrt{\frac{2}{\pi }}t\right)\end{array}}$

• Si la velocidad inicial del cuerpo V₀>V_T la fuerza de rozamiento es proporcional al cuadrado de la velocidad, mientras la velocidad del cuerpo se mantenga superior a V_T.

${\displaystyle \begin{array}{l}\frac{dV}{dt}=-\frac{\rho m(1+e)}{M}{V}^2\\ {\displaystyle \underset{V_0}{\overset{V}{\int }}\frac{dV}{V^2}}=-\frac{\rho m(1+e)}{M}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \frac{1}{V}=\frac{1}{V_0}+kt\end{array}}$

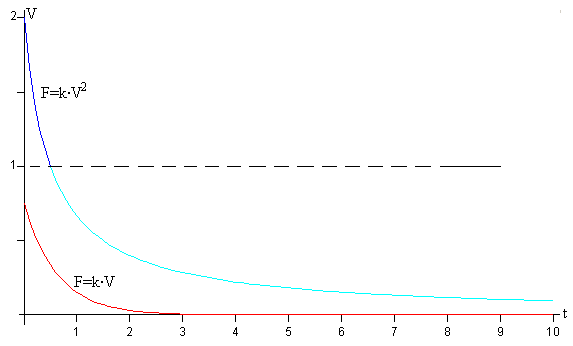
En la figura, se muestra la representación gráfica de la velocidad del cuerpo V en función del tiempo t. La velocidad V_T de las moléculas se tomado como unidad.

• La curva de color rojo describe la velocidad del cuerpo cuando su velocidad inicial V₀=0.75, por tanto la fuerza de rozamiento es proporcional a la velocidad V.
• La curva de color azul, describe la velocidad del cuerpo cuando su velocidad inicial V₀=2.0, por tanto la fuerza de rozamiento es proporcional al cuadrado de la velocidad mientas V<V_T.

Actividades

Se introduce

• La velocidad inicial V₀ del cuerpo,en el control titulado Velocidad inicial

Se pulsa el botón titulado Nuevo

En el programa se ha fijado:

• La masa de las moléculas m=1.0
• La masa del cuerpo M=100.0
• La temperatura T del gas unidimensional o bien, la raíz cuadrada de la velocidad cuadrática media V_T=1
• El coeficiente de restitución, e=1, los choques son elásticos.

Observamos que el cuerpo representado por un segmento rojo disminuye su velocidad debido a los choques con las moléculas del gas unidimensional, puntos de color azul.

Para ver con más detalle las moléculas y evitar su superposición, se mueven a lo largo de líneas horizontales separadas un píxel. Las moléculas no chocan entre sí.

Las moléculas están uniformemente repartidas en el segmento [-10, 10], teóricamente deberían cubrir todo el eje X, el espacio comprendido entre (-∞, +∞)

• Las moléculas de la parte izquierda cuya velocidad v sea mayor que la velocidad del cuerpo V chocan, las otras no intervienen en el movimiento del cuerpo.
• Las moléculas de la parte derecha cuya velocidad v sea menor que la velocidad del cuerpo V chocan, las otras no intervienen en el movimiento del cuerpo.

Cuando se activa la casilla titulada Marca partícula, nos muestra las moléculas que próximamente van a chocar con el cuerpo. La longitud de la flecha es proporcional a la velocidad de las moléculas.

Referencias

Molina M. I. Body motion in a resistive medium at temperature T. Revista Mexicana de Física, 48 (2) Abril 2002, págs. 132-134