El número de moléculas cuyo módulo de velocidad esta comprendido entre v y v+dv y cuya dirección está comprendida entre φ y φ+dφ, θ y θ+dθ, es

${\displaystyle dn=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)v^2·\sin \theta ·dv·d\theta ·d\phi }$

Flujo

Se define el flujo Φ, como el número de moléculas que atraviesan la sección A por unidad de área y unidad de tiempo.

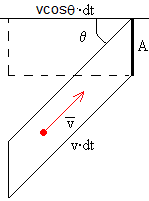
Calculamos primero, el número de moléculas con velocidad v que atraviesan el área A en el tiempo dt, que se mueven en una dirección que hace un ángulo θ con la normal a la sección, son las contenidas en el volumen cilíndrico de base A y altura v·cosθ·dt. Se multiplica el número de moléculas por unidad de volumen (dn/V) por el volumen del cilindro de la figura.

(dn/V)·A·v·cosθ·dt.

El número de moléculas con velocidad v que atraviesan la sección A por unidad de área y unidad de tiempo es

(dn/V)·v·cosθ

Para calcular la integral triple, establecemos los límites de integración para las variables v, φ y θ.

• Los límites de la primera integral respecto de φ, son 0 y 2π, se integra para todos los ángulos
• se integra para ángulos θ comprendidos entre 0 y π/2, ya que cuando θ>π/2, v·cosθ se hace negativa y la partícula se aleja de la pared.
• se integra para las velocidades, desde 0 a ∞.

El flujo es

${\displaystyle \begin{array}{l}\Phi =\frac{1}{V}{\displaystyle \int v·\cos \theta ·dn=}\\ \frac{1}{V}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)}}}(v·\cos \theta )·v^2\sin \theta ·dv·d\theta ·d\phi =\\ \frac{2\pi }{V}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\exp \left(-\frac{m{v}^2}{2kT}\right)v^3}}\cos \theta ·\sin \theta dv·d\theta =\\ \frac{\pi }{V}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\frac{m{v}^2}{2kT}\right)v^{3}dv}=\frac{N}{V}{\left(\frac{m}{2\pi kT}\right)}^{3/2}·2\pi ·\frac{1}{2}\frac{4k^2{T}^2}{2m^2}=\\ \frac{N}{V}\sqrt{\frac{kT}{2\pi m}}=\frac{1}{4}\frac{N}{V}<v>\end{array}}$

Para llegar a este resultado se han empleado las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \theta ·\sin \theta ·d\theta =\frac{1}{2}},\\ {\displaystyle \int x^3\exp (-\alpha x^2)dx},\{\begin{array}{l}u=x^2,du=2x·dx\\ dv=x\exp (-\alpha x^2)·dx,v=-\frac{1}{2\alpha }\exp (-\alpha x^2)\end{array}\\ =-\frac{x^2}{2\alpha }\exp (-\alpha x^2)+\frac{1}{\alpha }{\displaystyle \int x\exp (-\alpha x^2)}\\ =-\frac{x^2}{2\alpha }\exp (-\alpha x^2)-\frac{1}{2{\alpha }^2}\exp (-\alpha x^2)=-\frac{1}{2\alpha }\left\{x^2+\frac{1}{\alpha }\right\}\exp (-\alpha x^2)\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^3\exp (-\alpha x^2)dx=\frac{1}{2{\alpha }^2}}\end{array}}$

>> syms x;
>> syms a positive
>> int('x^3*exp(-a*x^2)',x,0,inf)
ans =1/(2*a^2)

Hemos calculado la velocidad media de las moléculas de un gas en la página anterior

${\displaystyle <v>=\frac{1}{N}{\displaystyle \int vdn=}\sqrt{\frac{8kT}{\pi m}}}$

Esta fórmula, tiene muchas aplicaciones algunas de las cuales estudiamos en esta página

${\displaystyle \Phi =\frac{N}{V}\sqrt{\frac{kT}{2\pi m}}}$

donde N es el número de moléculas, V es el volumen del gas ideal, m es la masa molecular y T es la temperatura.

Medida de la velocidad media de las moléculas

Cuando el recorrido libre medio de las moléculas encerradas en un recipiente es grande comparado con el diámetro de un pequeño orificio hecho en la pared del recipiente, la teoría cinética de los gases predice que el número de moléculas que escapan por unidad de área y por unidad de tiempo de un recipiente cuyo volumen es V y que contiene N moléculas es

${\displaystyle \Phi =\frac{1}{4}\frac{N}{V}<v>}$

Si el agujero tiene un área A, el recipiente va perdiendo moléculas a razón de Φ·A en la unidad de tiempo. La ecuación que nos da la variación del número N de moléculas del recipiente con el tiempo t es

${\displaystyle \frac{dN}{dt}=-\frac{1}{4}\frac{N}{V}<v>A}$

Empleando la ecuación de los gases ideales p·V=N·k·T

${\displaystyle \frac{dp}{dt}=-\frac{1}{4}\frac{<v>A}{V}p}$

Integrando entre la presión inicial p₀=1 atm en el instante t=0 y la presión final p en el instante t. Obtenemos la variación de la presión con el tiempo t.

${\displaystyle p=p_0\exp \left(-\frac{1}{4}\frac{<v>A}{V}t\right)}$

Un ejemplo dramático de aplicación de esta fórmula, consiste en la despresurización de una nave espacial a consecuencia del choque de un pequeño meteorito que logre perforar sus paredes. Supongamos una nave espacial  de 20 m³, que contiene oxígeno a la temperatura de 20º C y a la presión de 1 atm. El meteorito hace un pequeño agujero de 1 cm² por el que se escapa el gas. Determinar la presión del gas al cabo de 1 hora.

La velocidad media de las moléculas de oxígeno m=32 g a la temperatura de 293 K es

${\displaystyle <v>=\sqrt{\frac{8kT}{\pi m}}<v>=\sqrt{\frac{8·1.3805·{10}^{-23}·293}{\pi ·0.032/6.0225·{10}^{23}}}=440.3\text{m/s}}$

La presión p del oxígeno en la nave espacial al cabo de una hora t=3600 s, será

${\displaystyle p\text{=1·exp}\left(\text{-}\frac{\text{440}{\text{.3·10}}^{\text{-4}}}{\text{4·20}}3600\right)=0.14\text{atm}}$

Como actividad, se va a realizar un experimento que nos permita calcular la velocidad media de las moléculas del gas a partir de la medida de la variación de la presión p del recipiente en función del tiempo t.

Actividades

Se introduce

• El gas, eligiéndolo en el control titulado Gases.
• La temperatura (en K), en el control titulado Temperartura
• El área del orificio practicado en el recipiente (en mm²), en el control titulado Area orificio.
• La presión inicial p₀ se ha fijado en 1 atm
• El volumen V del recipiente se ha fijado en 3.5 litros.

Se pulsa el botón titulado Nuevo.

Se observa, como disminuye la presión a medida que se escapan las moléculas del gas por el orificio practicado en el recipiente.

En la parte derecha, hay un manómetro de mercurio que nos señala la presión p en cada instante t. En la parte izquierda, se representa la presión (en atm) en el eje vertical, en función del tiempo (en minutos) en el eje horizontal.

Datos

• Constante de Boltzmann k= 1.3805·10^-23 J/K

• Número de Avogadro N_A=6.0225·10²³ mol^-1

• Densidad del mercurio ρ=13550 kg/m³

• Presión atmosférica p₀=1 atm=1.013·10⁵ Pa

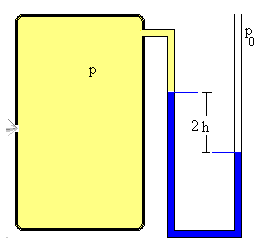
Para medir la presión se utiliza un manómetro de mercurio. Como el gas sale del recipiente su presión disminuye hasta que se hace cero (en un tiempo teóricamente infinito). En el manómetro abierto, las dos ramas estarán equilibradas (a la misma altura) en el instante inicial cuando la presión del gas contenido en el recipiente es p₀=1.0 atm.

Cuando la presión p del recipiente disminuye hay una diferencia 2h en el nivel en las dos ramas del líquido manométrico. La diferencia de presión

p₀-p=ρg2h

La diferencia de las alturas de las dos ramas del líquido manométrico es de 2·13.5 cm. Calcular la presión p en el recipiente

p=1.013·10⁵-13550·9.8·2·0.135=65447 Pa

p=65447/1.013·105=0.64 atm

Sea un recipiente de V=3.5 litros que contiene Neón a la temperatura de T=293 K. Se hace un orificio en el recipiente de área A=0.1 mm². Determinar la velocidad media de las moléculas de neón a dicha temperatura.

y conocida el área del orificio A y el volumen del recipiente V, determinamos la velocidad media <v> de las moléculas del gas elegido a la temperatura dada T.

Los resultados “experimentales” se representan en “papel semilogarítmico”, tal como se muestra en la figura.

t=(0:2:10)*60; %segundos
p=[1,0.51,0.26,0.13,0.07,0.03]; %presión
plot(t,log(p),'ro','markersize',4,'markerfacecolor','r')
grid on
xlabel('t(s)')
ylabel('log(p)')
title('Efusión de un gas')

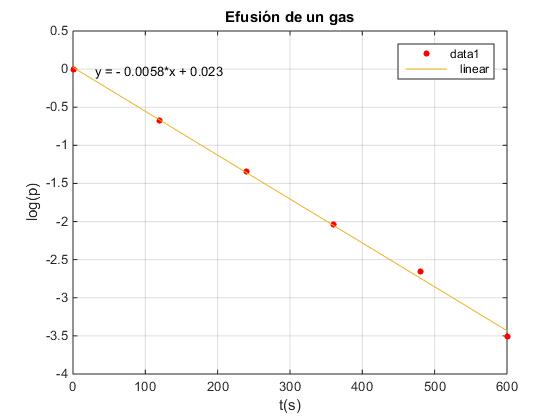
A partir de esta gráfica calculamos la constante de tiempo

${\displaystyle \frac{1}{4}\frac{<v>A}{V}}$

El ajuste de los datos 'experimentales' a una línea recta nos da una pendiente de -0.005758. A partir de este dato obtenemos la velocidad media de las moléculas

${\displaystyle \begin{array}{l}0.005758=\frac{<v>A}{4·V}\\ <v>=\frac{0.005758·4·3.5·{10}^3}{0.1·{10}^{-6}}=806.1\text{m/s}\end{array}}$

Calculamos la velocidad media de las moléculas para la temperatura de 293 K

${\displaystyle <v>=\sqrt{\frac{8kT}{\pi m}}<v>=\sqrt{\frac{8·1.3805·{10}^{-23}·293}{\pi ·0.1/6.0225·{10}^{23}}}=787.6\text{m/s}}$

Distribución de las velocidades de las moléculas del haz

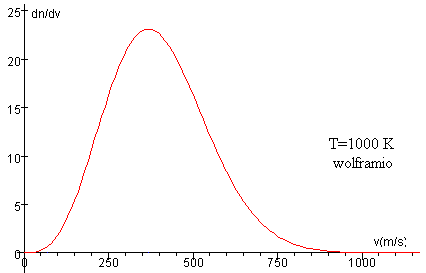
Si se hace un pequeño orificio en la pared de un horno que contiene un gas a temperatura T. El número de moléculas con velocidad entre v y v+dv que escapan por unidad de área y por unidad de tiempo es

${\displaystyle \begin{array}{l}d{n}_z={\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)(v·\cos \theta )·v^2\sin \theta ·dv·d\theta ·d\phi }}=\\ N\pi {\left(\frac{m}{2\pi kT}\right)}^{3/2}·v^3\exp \left(-\frac{m{v}^2}{2kT}\right)dv\end{array}}$

La velocidad media de las moléculas que escapan es

${\displaystyle <v_z>=\frac{1}{\Phi }{\displaystyle \underset{0}{\overset{\infty }{\int }}v·d{n}_z}=\frac{4}{N<v>}N\pi {\left(\frac{m}{2\pi kT}\right)}^{3/2}{\displaystyle \underset{0}{\overset{\infty }{\int }}{v}^4\exp \left(-\frac{m{v}^2}{2kT}\right)dv}=\frac{3}{8}\sqrt{\frac{2\pi kT}{m}}}$

Para llegar a este resultado, se ha empleado el resultado de la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^4\exp (-\alpha x^2)dx=}\frac{3}{8}\sqrt{\frac{\pi }{{\alpha }^5}}}$

>> syms x;
>> syms a positive;
>> int('x^4*exp(-a*x^2)',x,0,inf)
ans =(3*pi^(1/2))/(8*a^(5/2))

La velocidad media de las moléculas que salen a través del orificio no coincide con la velocidad media de las moléculas contenidas en un recipiente.

Referencias

Alonso, Finn. Física. Fundamentos cuánticos y estadísticos, Edt. Fondo Educativo Interamericano (1971). Problemas 10.29 y 10.30, pág. 471.

Para la experiencia simulada "Medida de la velocidad media de las moléculas"

Benenson. R. Molecular velocity determination through gas effusion: Intermediate laboratory experiment. Am. J. Phys. 37 (1) January 1969, pp. 39-46.