La energía de Fermi

Vamos a determinar cómo los electrones ocupan los niveles de energía. En la página titulada Distribución de la energía entre las moléculas de un gas ideal calculamos g(E), el número de niveles de energía comprendidos entre E y E+dE disponibles para una partícula libre encerrada en una caja de volumen V

${\displaystyle g(E)=\frac{4\pi V{(2m^3)}^{1/2}}{h^3}{E}^{1/2}}$

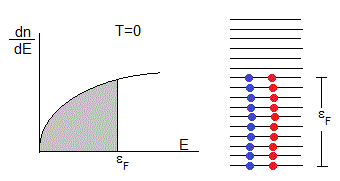
Cada nivel puede acomodar dos electrones (uno con espín hacia arriba y otro con espín hacia abajo).

${\displaystyle g(E)=\frac{8\pi V{(2m^3)}^{1/2}}{h^3}{E}^{1/2}}$

Si el metal está en su estado fundamental (en el cero absoluto de temperatura), todos los electrones ocupan los niveles más bajos de energía posibles, compatibles con el principio de exclusión de Pauli. Se denomina energía de Fermi, ε_F la energía del nivel más alto ocupado.

${\displaystyle N={\displaystyle \underset{0}{\overset{{\epsilon }_F}{\int }}g(E)dE}=\frac{8\pi V{(2m^3)}^{1/2}}{h^3}{\displaystyle \underset{0}{\overset{{\epsilon }_F}{\int }}{E}^{1/2}dE}=\frac{16\pi V{(2m^3)}^{1/2}}{3h^3}{\epsilon }_F^{3/2}}$

Si n₀=N/V es el número de electrones por unidad de volumen, la energía de Fermi ε_F es

${\displaystyle {\epsilon }_F=\frac{h^2}{8m}{\left(\frac{3n_0}{\pi }\right)}^{2/3}}$

Fuente: Física. Fundamentos Cuánticos y Estadísticos. Marcelo Alonso. Edward J. Finn. Fondo Educativo Interamericano. (1971), pág. 536

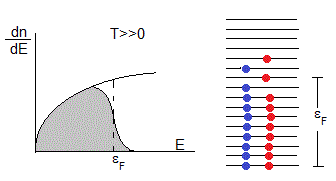
Supongamos que calentamos el metal a una temperatura T. Los electrones más próximos al nivel de Fermi pueden ser excitados térmicamente, ascendiendo de nivel de energía, tal como se muestra en la figura.

Hemos obtenido la fórmula la distribución de energía de las moléculas de un gas ideal. De un modo similar, el número de electrones por unidad de volumen cuya energía está comprendida entre E y E+dE viene dado por.

${\displaystyle dn=\frac{1}{\exp \left(\frac{E-{\epsilon }_F}{kT}\right)+1}\frac{8\pi {(2m^3)}^{1/2}}{h^3}{E}^{1/2}dE}$

El primer término indica que los electrones obedecen a la estadística de Fermi.

k=1.6021e-19/1.3805e-23; %electron-voltios/constante Boltzmann
EF=3.12; %energía de Fiemi del sodio
hold on
for T=[0,300,5000]
    f=@(x) sqrt(x)./(exp((x-EF)*k/T)+1);
    fplot(f,[0,6], 'displayName',num2str(T))
end
hold off
grid on
xlabel('E (eV)')
ylabel('dn/dE')
legend('-DynamicLegend','location','northeast')
title('Distribución de electrones')

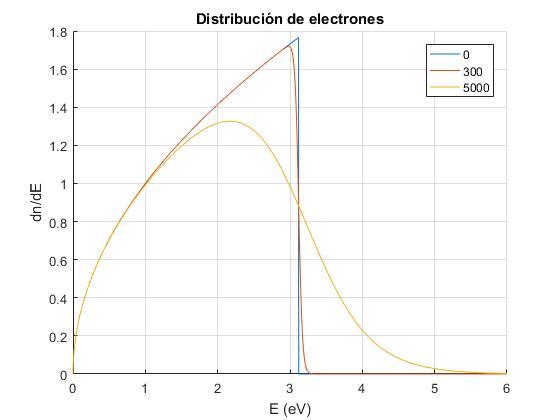
A temperatura ambiente, los electrones ocupan los niveles de energía hasta la energía de Fermi, ε_F. Para extraer un electrón del metal es necesario suministrarle una energía φ, esto es lo que ocurre por ejemplo, en el efecto fotoeléctrico, en el cual solamente se emiten fotoelectrones si hf>φ, la cantidad φ se denomina energía de arranque del metal. A temperaturas altas, sin embargo, la ocupación de estados electrónicos se extiende bien por encima de ε_F. Si la temperatura es suficientemente alta, los electrones adquieren energías mayores que ε_F+φ y escapan del metal (se evaporan). Este proceso se denomina emisión termoiónica y es la base del funcionamiento de las válvulas electrónicas.

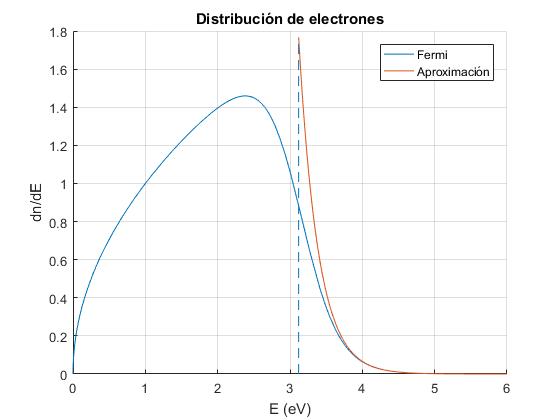
Para los electrones cuya energía E es mayor que la del nivel de Fermi, ε_F, la exponencial en el denominador es mucho mayor que la unidad y se puede aproximar a la expresión,

${\displaystyle \frac{1}{\exp \left(\frac{E-{\epsilon }_F}{kT}\right)+1}\approx \exp \left(-\frac{E-{\epsilon }_F}{kT}\right)}$

k=1.6021e-19/1.3805e-23; %electron-voltios/constante Boltzmann
EF=3.12; %energía de Fiemi del sodio
hold on
T=3000;
f=@(x) sqrt(x)./(exp((x-EF)*k/T)+1);
g=@(x) sqrt(x).*exp(-(x-EF)*k/T);
fplot(f,[0,6])
fplot(g,[EF,6])
line([EF,EF],[0,g(EF)],'lineStyle','--')
hold off
grid on
xlabel('E (eV)')
ylabel('dn/dE')
legend('Fermi','Aproximación')
title('Distribución de electrones')

Emisión termoiónica

La fórmula de Richardson calcula la densidad de corriente J_x de los electrones que escapan en la dirección perpendicular a la superficie del metal calentado a la temperatura T, es decir, de aquellos cuya componente v_x de la velocidad es superior a la mínima

${\displaystyle \frac{1}{2}m{v}_{x\mathrm{,.}\min }^2={\epsilon }_F+\phi }$

La densidad de corriente J_x es el producto de la carga q del electrón por el número de electrones dn cuya velocidad está comprendida entre v_x y v_x+dv_x y por la velocidad v_x de estos electrones siempre que sea superior a la mínima

Procedemos de forma similar al estudio de la sublimación de un sólido

${\displaystyle \begin{array}{l}{J}_x={\displaystyle \underset{v_{x,\min }}{\overset{\infty }{\int }}q{v}_{x}dn=q\frac{8\pi {(2m^3)}^{1/2}}{h^3}}{\displaystyle \underset{v_{x,\min }}{\overset{\infty }{\int }}{v}_x\frac{1}{\exp \left(\frac{E-{\epsilon }_F}{kT}\right)+1}{E}^{1/2}dE}\\ \approx q\frac{2m^3}{h^3}{\displaystyle \underset{v_{x,\min }}{\overset{\infty }{\int }}{v}_x\exp \left(-\frac{m{v}^2/2-{\epsilon }_F}{kT}\right)4\pi v^{2}dv}\end{array}}$

Recordando la equivalencia de las dos formas en las que se expresa la fórmula de la distribución de velocidades de las moléculas de un gas ideal.

${\displaystyle \begin{array}{l}{J}_x\approx q\frac{2m^3}{h^3}\exp \left(\frac{{\epsilon }_F}{kT}\right)\\ {\displaystyle \underset{v_{x,\min }}{\overset{\infty }{\int }}{v}_x\exp \left(-\frac{m{v}_x^2}{2kT}\right)d{v}_x}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{m{v}_y^2}{2kT}\right)d{v}_y}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{m{v}_z^2}{2kT}\right)d{v}_z}\end{array}}$

Teniendo en cuenta, los resultados de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{a}{\overset{\infty }{\int }}x\exp \left(-\alpha x^2\right)}dx=\frac{\exp \left(-\alpha a^2\right)}{2\alpha }\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\alpha x^2\right)}dx=\sqrt{\frac{\pi }{\alpha }}\end{array}}$

Llegamos a la ecuación de Richardson

${\displaystyle \begin{array}{l}{J}_x\approx q\frac{4\pi {\left(kT\right)}^{2}m}{h^3}\exp \left(\frac{{\epsilon }_F}{kT}\right)\exp \left(-\frac{{\epsilon }_F+\phi }{kT}\right)=q\frac{4\pi {\left(kT\right)}^{2}m}{h^3}\exp \left(-\frac{\phi }{kT}\right)=\\ A{T}^2\exp \left(-\frac{\phi }{kT}\right)\end{array}}$

Calculamos el valor del parámetro A a partir de las constantes fundamentales: k=1.3805·10^-23 J/K, h=6.6256·10^-34 J·s, q=1.6021·10^-19 C, m=9.1091·10^-31 kg. El valor de A=1 201 634 A/(m²K²)

Fuente: Física. Fundamentos Cuánticos y Estadísticos. Marcelo Alonso. Edward J. Finn. Fondo Educativo Interamericano. (1971), pág. 539

k=1.6021e-19/1.3805e-23; %electron-voltios/constante Boltzmann
phi=1.8; %energía de arranque del Cesio
A=120;
f=@(x) A*(x.^2).*exp(-phi*k./x);
T=1500:10:3000;
semilogy(T,f(T))
grid on
xlabel('T')
ylabel('J (A/cm^2)')
title('Ecuación de Richardson')

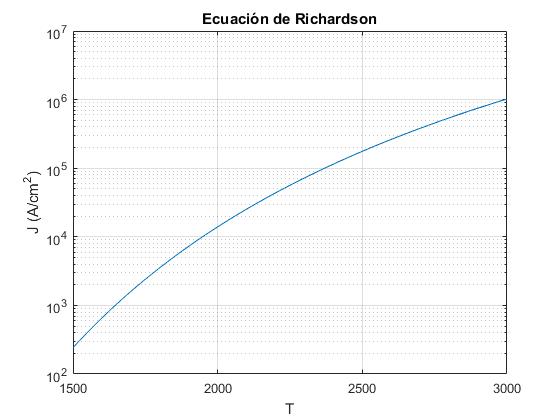
La emisión de electrones es muy sensible a las condiciones de la superficie y a la orientación de ésta respecto a la red cristalina del metal. La tabla proporciona algunos valores experimentales de la energía de arranque φ en eV y del parámetro A para diversos metales.

Corriente termoiónica

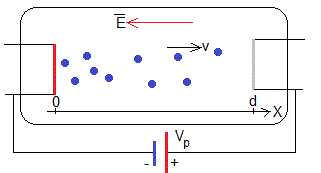
Si aplicamos una diferencia de potencial V_p entre dos metales y calentamos el cátodo, los electrones emitidos constituyen una corriente que va del cátodo al ánodo.

Situamos el origen en el cátodo y el eje X perpendicular al plano de los electrodos. Supongamos que el potencial del cátodo es nulo y y el potencial del ánodo es V_p. Las superficies equipotenciales son planos paralelos a los electrodos, la ecuación de Poisson aplicada al espacio entre los electrodos es

${\displaystyle \frac{d^{2}V}{d{x}^2}=-\frac{\rho }{{\epsilon }_0}}$

Si n(x) es el número de electrones por unidad de volumen en el espacio entre los electrodos a una distancia x del cátodo y e la carga de cada electrón, ρ(x)=-n(x)|e| es la densidad de carga

Supongamos que los electrones emitidos por el cátodo no tienen apenas velocidad inicial cuando salen de su superficie. Los electrones son acelerados por el campo eléctrico E existente entre los dos electrodos

${\displaystyle \frac{1}{2}{m}_e{v}^2(x)=\left|e\right|V(x)}$

Donde m_e es la masa del electrón. La densidad de corriente, la carga que fluye en la unidad de tiempo a través de la unidad de área, es |j|=|e|n(x)v(x)=ρ(x)v(x). En el estado estacionario, j deberá ser constante.

Resolvemos la ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d^{2}V}{d{x}^2}=\frac{1}{{\epsilon }_0}\frac{\left|j\right|}{v(x)}\\ \frac{d^{2}V}{d{x}^2}=\frac{\left|j\right|}{{\epsilon }_0}\sqrt{\frac{m}{2\left|e\right|V}}=\frac{\alpha }{\sqrt{V}}\end{array}}$

con las condiciones iniciales, V(x)=0, dV/dx=0 para x=0. El campo eléctrico y el potencial son nulos en la superficie del cátodo caliente. Multiplicando ambos miembros por dV/dx

${\displaystyle \begin{array}{l}\frac{d^{2}V}{d{x}^2}\frac{dV}{dx}=\frac{\alpha }{\sqrt{V}}\frac{dV}{dx}\\ \frac{1}{2}\frac{d}{dx}{\left(\frac{dV}{dx}\right)}^2=2\alpha \frac{d}{dx}\sqrt{V}\end{array}}$

Integramos ambos miembros entre x=0 y x

${\displaystyle \begin{array}{l}{\left(\frac{dV}{dx}\right)}^2-{\left(\frac{dV}{dx}\right)}_{x=0}^2=4\alpha \left(\sqrt{V}-0\right)\\ {\left(\frac{dV}{dx}\right)}^2=4\alpha \sqrt{V}\\ \frac{dV}{V^{1/4}}=2\sqrt{\alpha }·dx\end{array}}$

Integramos esta ecuación diferencial sabiendo que para x=0, V=0 y para x=d, V=V_p. Siendo d la distancia entre los electrodos

${\displaystyle \begin{array}{l}\frac{4}{3}{V}_p^{3/4}=2\sqrt{\alpha }d\\ V_p^{3/2}=\frac{9}{4}\alpha d^2\\ V_p^{3/2}=\frac{9}{4}\frac{\left|j\right|}{{\epsilon }_0}\sqrt{\frac{m}{2\left|e\right|}}{d}^2\\ \left|j\right|=\frac{4{\epsilon }_0}{9d^2}\sqrt{\frac{2\left|e\right|}{m}}·V_p^{3/2}\end{array}}$

La densidad de corriente no sigue la ley de Ohm crece con la potencia 3/2 de la diferencia de potencial V_p. Se trata de un ejemplo de un comportamiento no lineal bastante general en el que la corriente no siempre es proporcional a la diferencia de potencial.

Cuando la diferencia de potencial es grande se observan desviaciones de esta ley, debido a que la carga entre electrodos disminuye y ya no es posible cumplir la condición de que dV/dx=0 para x=0 (campo eléctrico nulo en la superficie del cátodo caliente).

Referencias

Física. Fundamentos Cuánticos y Estadísticos. Marcelo Alonso. Edward J. Finn. Fondo Educativo Interamericano. (1971)

A. N. Matveev. Electricity and Magnetism. 1986, Mir Pubishers. pp. 236-238