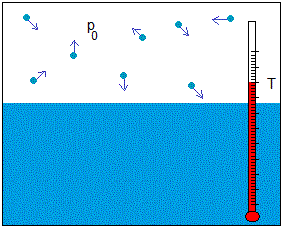
Supongamos un líquido en equilibrio con su fase de vapor. Consideremos el vapor como un gas ideal. La siguiente ecuación nos da el número de moléculas que chocan con la superficie del líquido por unidad de área y en la unidad de tiempo

${\displaystyle \Phi =\frac{N}{V}\sqrt{\frac{kT}{2\pi m}}}$

donde N es el número de moléculas de vapor, V es el volumen del gas, m es la masa molecular y T es la temperatura.

Consideremos una fase líquida (o sólida) en equilibrio con su propio vapor a una temperatura dada. Este equilibrio es dinámico en el sentido de que las moléculas de vapor chocan constantemente con la superficie del líquido y al mismo tiempo, las moléculas del líquido pasan a la fase de vapor. La masa evaporada en la unidad de tiempo se iguala a la masa condensada

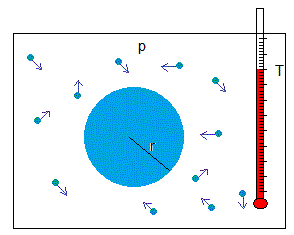
Sea una gota de radio r. La ecuación de Ostwald-Freundlich nos dice que la presión de vapor p de la gota es superior a la del mismo líquido en una superficie plana p₀, ambas a la misma temperatura T

${\displaystyle p=p_0\exp \left(\frac{r_c}{r}\right),r_c=\frac{2\gamma m}{\rho kT}}$

• γ es la tensión superficial del líquido
• ρ es la densidad
• m es la masa de una molécula

Aplicando la ecuación de los gases ideales pV=NkT

${\displaystyle \Phi =\frac{N}{V}\sqrt{\frac{kT}{2\pi m}}=\frac{p}{kT}\sqrt{\frac{kT}{2\pi m}}=\frac{p}{\sqrt{2\pi mkT}}=\frac{p_0\exp \left(\frac{r_c}{r}\right)}{\sqrt{2\pi mkT}}}$

El número de moléculas N_l que hay en una gota de radio r es

${\displaystyle N_l=\frac{\rho \frac{4}{3}\pi r^3}{m}}$

El número de moléculas de la gota cambia al variar el radio dr

${\displaystyle d{N}_l=\frac{4}{3}\pi \frac{\rho }{m}3r^{2}dr=4\pi \frac{\rho }{m}{r}^{2}dr}$

Si ese cambio ocurre en un intervalo de tiempo ddt

${\displaystyle \frac{d{N}_l}{dt}=4\pi \frac{\rho }{m}{r}^2\frac{dr}{dt}}$

El número de moléculas y por tanto, el radio de la gota disminuye con el tiempo debido a la evaporación

${\displaystyle \begin{array}{l}\frac{d{N}_l}{dt}=-\Phi \left(4\pi r^2\right)\\ 4\pi \frac{\rho }{m}{r}^2\frac{dr}{dt}=-\frac{p_0\exp \left(\frac{r_c}{r}\right)}{\sqrt{2\pi mkT}}4\pi r^2\\ \frac{dr}{dt}=-\frac{p_0\exp \left(\frac{r_c}{r}\right)}{\rho }\sqrt{\frac{m}{2\pi kT}}\end{array}}$

Separando variables

${\displaystyle \exp \left(-\frac{r_c}{r}\right)dr=-\frac{p_0}{\rho }\sqrt{\frac{m}{2\pi kT}}dt}$

Dividiendo entre r_c

${\displaystyle \begin{array}{l}\exp \left(-\frac{r_c}{r}\right)d\left(\frac{r}{r_c}\right)=-\frac{p_0}{\rho r_c}\sqrt{\frac{m}{2\pi kT}}dt\\ \exp \left(-\frac{r_c}{r}\right)d\left(\frac{r}{r_c}\right)=-\frac{p_0}{2\gamma }\sqrt{\frac{kT}{2\pi m}}dt\\ \exp \left(-\frac{r_c}{r}\right)d\left(\frac{r}{r_c}\right)=-\frac{1}{t_c}dt,t_c=\frac{2\gamma }{p_0}\sqrt{\frac{2\pi m}{kT}}\end{array}}$

Llamamos u=r/r_c y τ=t/t_c

${\displaystyle \begin{array}{l}\exp \left(-\frac{1}{u}\right)du=-d\tau \\ {\displaystyle \int \exp \left(-\frac{1}{u}\right)du=-\tau +c}\end{array}}$

Para resolver la integral, hacemos el cambio de variable

${\displaystyle \begin{array}{l}u=-\frac{1}{t},du=\frac{dt}{t^2}\\ {\displaystyle \int \exp \left(-\frac{1}{u}\right)du}={\displaystyle \int \frac{e^t}{t^2}dt}\end{array}}$

Integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{e^t}{t^2}dt},\{\begin{array}{l}v=e^t,dv=e^{t}dt\\ dw=\frac{dt}{t^2},w=-\frac{1}{t}\end{array}\\ =-\frac{e^t}{t}+{\displaystyle \int \frac{e^t}{t}}dt\end{array}}$

El resultado es

${\displaystyle {\displaystyle \int \exp \left(-\frac{1}{u}\right)du}=u\exp \left(-\frac{1}{u}\right)+\text{Ei}\left(-\frac{1}{u}\right)}$

Ei(x) es la función integral exponencial. Comprobamos con Math Symbolic de MATLAB

>> syms x;
>> int(exp(-1/x),x)
 ans =ei(-1/x) + x*exp(-1/x)

La función implícita τ=f(u) es

${\displaystyle u\exp \left(-\frac{1}{u}\right)+\text{Ei}\left(-\frac{1}{u}\right)=-\tau +c}$

La constante c se determina sabiendo que u=1 en el instante inicial τ=0

${\displaystyle c\text{=Ei}\left(-1\right)+\frac{1}{e}}$

La función implícita que vamos a representar es

${\displaystyle \tau =\text{Ei}\left(-1\right)+\frac{1}{e}-\text{Ei}\left(-\frac{1}{u}\right)-u\exp \left(-\frac{1}{u}\right)}$

tau=@(x) ei(-1)+1/exp(1)-ei(-1./x)-x.*exp(-1./x);
fp=fplot(tau,[0.1,1]);
plot(fp.YData, fp.XData)
grid on
xlabel('\tau')
ylabel('u')
title('Evaporación de una gota')

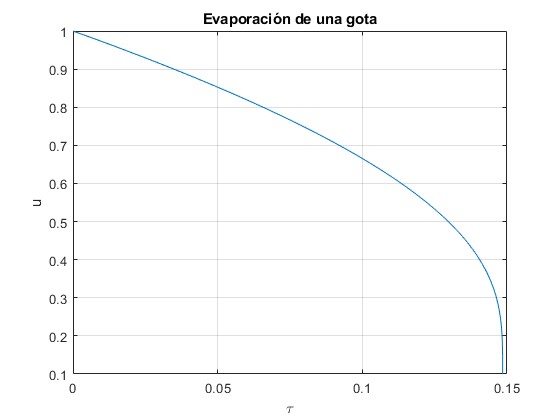
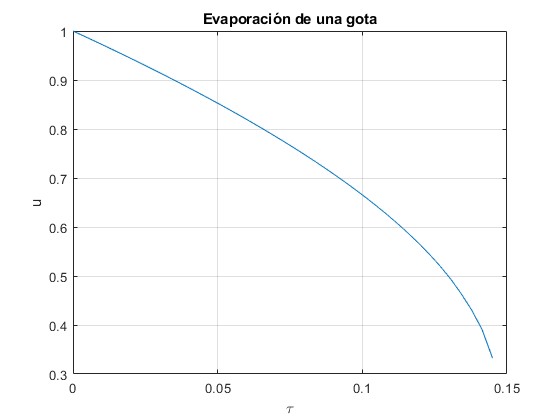
Que vamos a comparar con la solución numérica de la ecuación diferencial

${\displaystyle \frac{du}{d\tau }=-\exp \left(\frac{1}{u}\right)}$

f=@(t,x) -exp(1/x); 
[t,x]=ode45(f,[0,0.145],1); 
plot(t,x)
grid on
xlabel('\tau')
ylabel('u')
title('Evaporación de una gota')

Gota de radio grande

Para gotas de radio grande, cuyo radio r es mucho mayor que r_c o u>>1, la ecuación diferencial se puede aproximar a

${\displaystyle \begin{array}{l}\frac{du}{d\tau }\approx -1\\ dr=-\frac{r_c}{t_c}dt\\ r=r_0-\frac{r_c}{t_c}t\\ \frac{r_c}{t_c}=\frac{\frac{2\gamma m}{\rho kT}}{\frac{2\gamma }{p_0}\sqrt{\frac{2\pi m}{kT}}}=\frac{p_0}{\rho }\sqrt{\frac{m}{2\pi kT}}\end{array}}$

El radio de la gota decrece linealmente con el tiempo. Cuando el radio r de la gota es del orden de r_c (≈10^-9 m), disminuye rápidamente de acuerdo a la función implícita descrita. Esencialmente, el radio de la gota disminuye linealmente con el tiempo

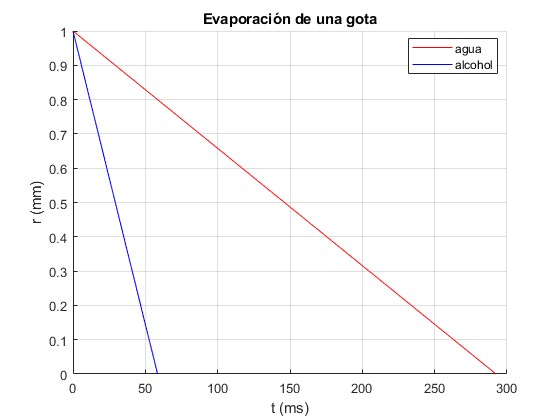
Representamos el radio de una gota de agua y de alcohol etílico en función del tiempo. Radio inicial r₀= 1 mm, en el instante t=0

Datos

k1=3.42e-3; %agua
k2=1.71e-2; %alcohol etílico
r0=1e-3; %radio en m
T1=r0/k1;
T2=r0/k2;
line([0,T1*1000],[r0*1000,0],'color','r')
line([0,T2*1000],[r0*1000,0],'color','b')
grid on
xlabel('t (ms)')
ylabel('r (mm)')
legend('agua', 'alcohol','location','best')
title('Evaporación de una gota')

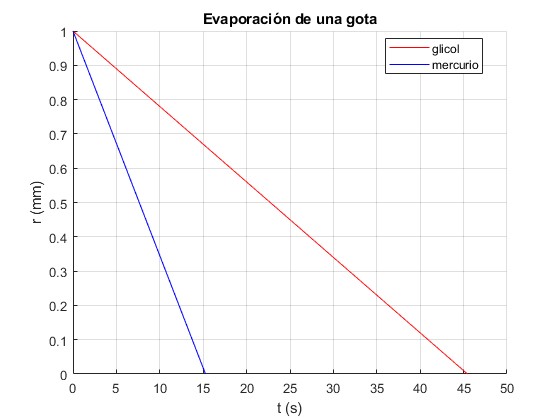
Representamos el radio de una gota de mercurio y de glicol de etileno en función del tiempo. Radio inicial r₀= 1 mm

Datos

k3=2.20e-5; %glicol de etileno
k4=6.55e-5; %mercurio
r0=1e-3; %radio en m
T3=r0/k3;
T4=r0/k4;
line([0,T3],[r0*1000,0],'color','r')
line([0,T4],[r0*1000,0],'color','b')
grid on
xlabel('t (s)')
ylabel('r (mm)')
legend('glicol', 'mercurio','location','best')
title('Evaporación de una gota')

Hemos supuesto hasta ahora que la gota se evapora en el vacío. En el aire o con humedad, muchas de las moléculas que se han evaporado regresan a la superficie del líquido y esto afecta al tiempo de evaporación

Referencias

Pirooz Mohazzabi, Gabrielle A. Richardson, Gwendolyn A. Richardson. A Model for Droplet Evaporation. Journal of Applied Mathematics and Physics. 11, 1837-1845 (2023)