Una molécula de masa m se mueve con velocidad u, cuya componente horizontal es u_x, choca con el émbolo de masa M que se mueve hacia la derecha con velocidad v.

Supondremos que las moléculas chocan elásticamente con el émbolo y las paredes del recipiente. Esta suposición es razonable, si consideramos que en un proceso adiabático no hay intercambio de energía en forma de calor a través de las paredes del recipiente con el entorno

Aplicamos la conservación del momento lineal y la energía cinética

${\displaystyle \{\begin{array}{l}m{u}_x+Mv=m{u}_x^{\text{'}}+Mv\text{'}\\ \frac{1}{2}m{u}_x^2+\frac{1}{2}M{v}^2=\frac{1}{2}m{\left(u_x^{\text{'}}\right)}^2+\frac{1}{2}M{\left(v\text{'}\right)}^2\end{array}}$

Despejaremos las velocidades después del choque en este sistema de dos ecuaciones

${\displaystyle \{\begin{array}{l}m\left(u_x-u_x^{\text{'}}\right)=M\left(v\text{'}-v\right)\\ m\left(u_x^2-{\left(u_x^{\text{'}}\right)}^2\right)=M\left({\left(v\text{'}\right)}^2-v^2\right)\end{array}}$

Simplificamos la segunda ecuación

${\displaystyle m\left(u_x-u_x^{\text{'}}\right)\left(u_x+u_x^{\text{'}}\right)=M\left(v\text{'}-v\right)\left(v\text{'}+v\right)}$

Resolvemos el sistema de dos ecuaciones con dos incógnitas

${\displaystyle \{\begin{array}{l}{u}_x+u_x^{\text{'}}=v\text{'}+v\\ m\left(u_x-u_x^{\text{'}}\right)=M\left(v\text{'}-v\right)\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}v\text{'}=\frac{M-m}{M+m}v+2\frac{m}{m+M}{u}_x=\frac{1-\frac{m}{M}}{1+\frac{m}{M}}v+\frac{\frac{m}{M}}{1+\frac{m}{M}}{u}_x\\ u_x^{\text{'}}=2\frac{M}{m+M}v-\frac{M-m}{M+m}{u}_x=2\frac{1}{1+\frac{m}{M}}v-\frac{1-\frac{m}{M}}{1+\frac{m}{M}}{u}_x\end{array}}$

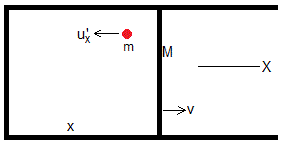
La masa de una molécula es mucho menor que la masa del émbolo, m<<M y también, la velocidad media de las moléculas es mucho mayor que la velocidad del desplazamiento del émbolo u_x>>v

${\displaystyle \{\begin{array}{l}v\text{'}\approx v\\ u_x^{\text{'}}\approx 2v-u_x\end{array}}$

Se cumple además

${\displaystyle {\left(u_x^{\text{'}}\right)}^2\approx {\left(u_x\right)}^2-4v{u}_x}$

En cada impacto hay un cambio de energía.

${\displaystyle \Delta \left(\frac{1}{2}m{u}_x^2\right)=\frac{1}{2}m{\left(u_x^{\text{'}}\right)}^2-\frac{1}{2}m{\left(u_x\right)}^2=-\frac{1}{2}m·4v{u}_x=-2mv{u}_x}$

La energía cinética media de las moléculas de un gas ideal es

${\displaystyle \langle \frac{1}{2}m{u}^2\rangle =\frac{1}{2}m\langle u_x^2\rangle +\frac{1}{2}m\langle u_y^2\rangle +\frac{1}{2}m\langle u_z^2\rangle =\frac{3}{2}kT}$

La energía E de un mol de gas se relaciona con la temperatura T

${\displaystyle E=N_A\langle \frac{1}{2}m{u}^2\rangle =\frac{3}{2}{N}_{A}kT=\frac{3}{2}RT}$

N_A es el número de Avogadro

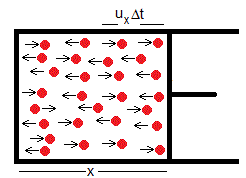
En el intervalo de tiempo comprendido entre t y t+Δt chocan con el émbolo, las moléculas contenidas en el volumen

${\displaystyle \frac{1}{2}n\left(A{u}_x\Delta t\right)}$

Siendo A el área del émbolo y n es el número de moléculas por unidad de volumen. El factor 1/2 se refiere a que de las moléculas contenidas en este volumen, la mitad (en promedio) se dirigen hacia el émbolo u_x>0 y la otra mitad, se alejan del émbolo u_x<0

Para un mol de gas, el número de moléculas por unidad de volumen es

${\displaystyle n=\frac{N_A}{Ax}}$

En el intervalo de tiempo comprendido entre t y t+Δt, chocan con el émbolo

${\displaystyle \frac{1}{2}\left(\frac{N_A}{Ax}\right)\left(A{u}_x\Delta t\right)=\frac{1}{2}{N}_A\frac{u_x}{x}\Delta t}$

El cambio de energía del gas ideal en el intervalo de tiempo comprendido entre t y t+Δt es el producto del número de choques por el cambio de energía en cada choque

${\displaystyle \Delta E=\left(\frac{1}{2}{N}_A\frac{u_x}{x}\Delta t\right)\Delta \left(\frac{1}{2}m{u}_x^2\right)=\frac{1}{2}{N}_A\frac{u_x}{x}\Delta t\left(-2mv{u}_x\right)=-2N_A\langle \frac{1}{2}m{u}_x^2\rangle \frac{v}{x}\Delta t=-2N_A\left(\frac{1}{2}kT\right)\frac{\Delta x}{x}=-N_{A}kT\frac{\Delta x}{x}}$

En el límite cuando Δt→0

${\displaystyle \begin{array}{l}\frac{3}{2}{N}_{A}kdT=-N_{A}kT\frac{dx}{x}\\ \frac{dT}{T}=-\frac{2}{3}\frac{dx}{x}\\ \frac{dT}{T}=-\frac{2}{3}\frac{dV}{V}\end{array}}$

El volumen del recipiente cilíndrico que contiene un mol de gas ideal, es V=A·x. Integramos

${\displaystyle \begin{array}{l}\ln T+\ln V^{2/3}=\text{cte}\\ T{V}^{2/3}=\text{cte}\end{array}}$

Gas ideal formado por una sola partícula

La pared fija está situada en x=0 y la pared móvil está situada inicialmente en la posición x₀ en el instante t=0. La pared móvil se mueve con velocidad constante u hacia la pared fija.

La posición de la pared móvil en el instante t es x=x₀-u·t. El movimiento de la partícula, cuya velocidad constante es v₀, encerrada entre ambas paredes se muestra en la figura y se describe a continuación

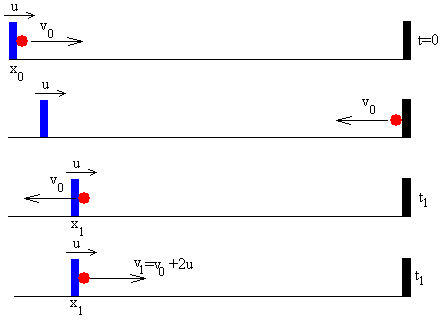
Primer choque:

La partícula parte en el instante t=0, de la posición x₀, se mueve hacia la pared fija con velocidad constante v₀. Choca con la pared fija cambiando el sentido de su velocidad y se dirige al encuentro de la pared móvil, que se produce en el instante t₁.

${\displaystyle t_1=\frac{2x_0}{u+v_0}}$

La posición de la pared móvil en dicho instante es x₁=x₀-u·t₁

Segundo choque:

Después del choque, velocidad de la partícula es v₁=v₀+2u y se dirige hacia la pared fija. Choca con la pared fija, cambiando el sentido de su velocidad y se dirige al encuentro de la pared móvil, que se produce en el instante t₂.

${\displaystyle t_2=t_1+\frac{2x_1}{u+v_1}}$

La posición de la pared móvil en dicho instante es x₂=x₀-u·t₂

Tercer choque:

Después del choque, la velocidad de la partícula es v₂=v₁+2u=v₀+2(2u) y se dirige hacia la pared fija. Choca con la pared fija, cambiando el sentido de su velocidad y se dirige al encuentro de la pared móvil, que se produce en el instante t₃.

${\displaystyle t_3=t_2+\frac{2x_2}{u+v_2}}$

La posición de la pared móvil en dicho instante es x₃=x₀-u·t₃

Choque n+1:

Después del choque n la velocidad de la partícula es v_n=v_n-1+2u=v₀+n(2u) y se dirige hacia la pared fija. Choca con la pared fija, cambiando el sentido de su velocidad y se dirige al encuentro de la pared móvil, que se produce en el instante t_n+1.

${\displaystyle t_{n+1}=t_n+\frac{2x_n}{u+v_n}}$

La posición de la pared móvil en dicho instante es x_n+1=x₀-u·t_n+1

La velocidad de la partícula va creciendo, con el número n de choques, alcanzando el valor

v_n =v₀+2nu

El desplazamiento de la pared móvil entre dos choques sucesivos que se producen en los instantes t_n y t_n+1 es

${\displaystyle \begin{array}{l}{x}_{n+1}-x_n=x_0-u\left(t_n+\frac{2x_n}{u+v_n}\right)-(x_0-u{t}_n)=\frac{-2x_{n}u}{u+v_0+2nu}\\ x_{n+1}-x_n=\frac{-2x_n}{(2n+1)+v_0/u}\end{array}}$

De la formulación discreta a la continua.

El parámetro macroscópico observable es la posición x de la pared móvil o el volumen del recipiente que contiene la partícula. Expresaremos la fuerza que ejerce la pared sobre la partícula, el trabajo y la energía cinética de la partícula en función de x.

Como x es una función de n podemos escribir de forma aproximada

${\displaystyle \frac{dx(n)}{dn}=\frac{-2x(n)}{(2n+1)+v_0/u}}$

Separando variables e integrando

${\displaystyle \begin{array}{l}-{\displaystyle \underset{x_0}{\overset{x}{\int }}\frac{dx}{2x}}={\displaystyle \underset{0}{\overset{n}{\int }}\frac{dn}{(2n+1)+v_0/u}}\\ -\frac{1}{2}\ln \frac{x}{x_0}=\frac{1}{2}\ln \frac{2n+1+v_0/u}{1+v_0/u}\end{array}}$

Despejando x

${\displaystyle x=\frac{x_0(1+v_0/u)}{2n+1+v_0/u}}$

El desplazamiento Δx de la pared móvil durante el intervalo de tiempo entre dos choques consecutivos es

${\displaystyle x_{n+1}-x_n\approx \Delta x=\frac{-2x}{2n+1+v_0/u}}$

La posición x de la pared móvil es función del número de choques n. La velocidad de la partícula v es también función del número de choques n, v=v₀+2nu. Expresamos la velocidad v de la partícula en función de la posición x de la pared móvil

${\displaystyle v=(u+v_0)\frac{x_0}{x}-u}$

Expresamos, igualmente el desplazamiento Δx en función de x

${\displaystyle \Delta x=\frac{-2xu}{v+u}=\frac{-2x^{2}u}{(u+v_0)x_0}}$

A partir de la expresión de x en función del número n de choques, despejamos n y derivamos respecto del tiempo.

${\displaystyle 2\frac{dn}{dt}=\frac{-x_0(1+v_0/u)}{x^2}\frac{dx}{dt}}$

Teniendo en cuenta que dx/dt=-u, la frecuencia f de los choques (número de choques en la unidad de tiempo) es

${\displaystyle f=\frac{dn}{dt}=\frac{x_0(u+v_0)}{2x^2}}$

El incremento de la frecuencia entre los choques se debe a dos causas:

• El incremento de la velocidad de la partícula después de cada choque en 2u
• La disminución del camino que ha de recorrer la partícula

Trabajo de la fuerza F que ejerce la pared móvil

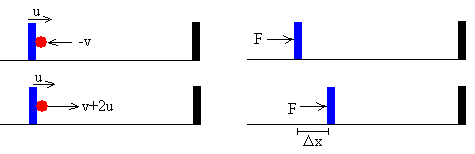
• Antes del choque la velocidad de la partícula es –v
• Después del choque la velocidad de la partícula es v+2u

El cambio de momento lineal en cada choque es  m(v+2u)-m(-v)=2m(u+v)

La fuerza F que ejerce la pared móvil se emplea en cambiar el momento lineal p de la partícula F=dp/dt. La fuerza F es el producto de la frecuencia de los choques por el cambio de momento lineal en cada choque.

${\displaystyle F=2m(u+v)f=m{(u+v_0)}^2\frac{x_0^2}{x^3}}$

El trabajo de la fuerza F cuando la pared móvil se desplaza Δx es

${\displaystyle -F·\Delta x=m{(u+v_0)}^2\frac{x_0^2}{x^3}·\frac{-2x^{2}u}{(u+v_0)x_0}=2mu(u+v_0)\frac{x_0}{x}}$

La variación de energía cinética en un choque es

${\displaystyle \Delta E_k=\frac{1}{2}m{\left(v+2u\right)}^2-\frac{1}{2}m{v}^2=2mu(u+v_0)\frac{x_0}{x}}$

El trabajo de de la fuerza F se invierte en incrementar la energía cinética de la partícula.

-F·Δx=ΔE_k

Relación entre las magnitudes microscópicas y los parámetros macroscópicos.

La energía cinética está relacionada con la temperatura, la fuerza con la presión y la posición de la pared móvil con el volumen del recipiente. Sustituimos:

• La presión p por la fuerza F

• El desplazamiento Δx por la variación de volumen dV

• El incremento de la energía cinética ΔE_k por la variación de la temperatura dT del sistema de partículas

-p·dV=k·dT

La ecuación de estado de los gases ideales relaciona, presión p, el volumen V y temperatura absoluta T.

${\displaystyle -\frac{nRT}{V}dV=kdT\frac{dT}{T}+\text{(}\gamma \text{-1)}\frac{dV}{V}=0}$

Integrando miembro a miembro, obtenemos la ecuación de una transformación adiabática.

${\displaystyle T{V}^{\gamma -1}=\text{cte}P{V}^{\gamma }=\text{cte}}$

donde γ al igual que k son constantes.

Actividades

Se introduce

• La velocidad u de la pared móvil, en el control titulado Velocidad pared móvil
• La velocidad inicial v₀=1 de la partícula, se ha fijado en el programa interactivo
• La posición inicial x₀=1 de la pared móvil también se ha fijado

Se pulsa en el botón titulado Nuevo

Se observa el movimiento de la partícula. En la parte superior izquierda, se proporciona el dato de la velocidad v de la partícula en cada instante t.

En la parte superior, se representan en dos gráficas la velocidad v de la partícula en función de la posición x del émbolo móvil.

• En color rojo, el movimiento real.
• En color azul, la aproximación continua dada por la fórmula

${\displaystyle v=(u+v_0)\frac{x_0}{x}-u}$

Referencias

E N Miranda. Adiabatic reversible compression: a molecular view. Eur. J. Phys. 23 (2002) pp. 389–393

Vermillon, R. Compresing a classical particle in a 1-D box. Am. J. Phys. 40, September 1978, pp. 1340-1342