Un cilindro de sección S y longitud L está cerrado por ambos extremos, contiene un émbolo que divide el volumen en dos partes A y B, ambos contienen la misma cantidad de un gas ideal, un mol. El cilindro y el émbolo están adiabáticamente aislados. El émbolo está sujeto de modo que los volúmenes iniciales de cada parte son, respectivamente  V₁₀=S·x₀, V₂₀=S(L-x₀). Las temperaturas iniciales del gas en cada una de las dos partes son T₁₀ y T₂₀.

En el instante t=0, se libera el pistón y suponemos que el émbolo se mueve sin rozamiento. Vamos a determinar el estado final de equilibrio.

El sistema alcanzará el equilibrio cuando las presiones de los gases separados por el émbolo sea la misma p_1f=p_2f=p_f

1. Aplicamos la ecuación de los gases ideales a cada una de las partes

p_f·V_1f=nRT_1f
p_f·V_2f=nRT_2f

2. Como el sistema es aislado, la energía total permanece constante

U_1f+U_2f=U₁₀+U₂₀

La energía interna de un gas ideal solamente depende de la temperatura

T_1f+T_2f=T₁₀+T₂₀

3. Los volúmenes de los gases cambian, pero el volumen total es constante e igual al inicial que ocupaban los gases.

V₁₀+V₂₀=V_1f+V_2f

Despejamos la temperaturas finales  y la presión final

${\displaystyle \begin{array}{l}{T}_{1f}=\frac{(T_{10}+T_{20})V_{1f}}{V_{1f}+V_{2f}}{T}_{2f}=\frac{(T_{10}+T_{20})V_{2f}}{V_{1f}+V_{2f}}\\ p_f=nR\frac{(T_{10}+T_{20})}{V_{1f}+V_{2f}}=nR\frac{(T_{10}+T_{20})}{V_{10}+V_{20}}\end{array}}$

Ahora bien, de estas ecuaciones no podemos despejar los volúmenes finales ni las temperaturas finales.

Una vez que se suelta el émbolo situado en la posición x₀, describe varias oscilaciones hasta que alcanza una posición de equilibrio final en el que las presiones a ambos lados del émbolo se igualan. Para determinar los volúmenes finales o las temperaturas finales necesitamos formular un modelo de gas ideal que nos describa la evolución desde el estado inicial al estado final de equilibrio.

Choque de las moléculas de un gas con un émbolo móvil

En la página, Oscilaciones de un émbolo. Aproximación al equilibrio, llegamos a la siguiente expresión cuando se estudiaron los choques de las moléculas de un gas con un émbolo que se mueve con velocidad u. La variación de energía interna U del gas es

${\displaystyle \begin{array}{l}dU=-4\pi m\frac{dV}{V}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\left\{u^2\frac{\sqrt{\pi }}{4}{\left(\frac{2kT}{m}\right)}^{3/2}-u\frac{1}{2}{\left(\frac{2kT}{m}\right)}^2+\frac{\sqrt{\pi }}{8}{\left(\frac{2kT}{m}\right)}^{5/2}\right\}=\\ -mN\frac{dV}{V}\left\{u^2-\frac{2}{\sqrt{\pi }}u{\left(\frac{2kT}{m}\right)}^{1/2}+\frac{1}{2}\left(\frac{2kT}{m}\right)\right\}\end{array}}$

Definimos nuevas variables:

• M_g=mN es la masa del gas (m es la masa de una molécula y N es el número de moléculas contenidas en el volumen V del gas). Para un mol de gas, N es el número de Avogadro, N·k=R=8.3143 J/(K·mol)

• u=dx/dt es la velocidad del émbolo (x es la posición del émbolo)

• V=S·x es el volumen del gas

• El cambio infinitesimal de volumen del gas es dV=S·dx=S·(dx/dt)dt

• dU=c_v·dT, es la variación de energía interna de un mol de gas ideal. c_v es el calor específico molar a volumen constante.

${\displaystyle c_v\frac{dT}{dt}=-\frac{RT}{x}\left(\frac{dx}{dt}\right)+\sqrt{\frac{8R{M}_g}{\pi }}\frac{\sqrt{T}}{x}{\left(\frac{dx}{dt}\right)}^2-\frac{M_g}{x}{\left(\frac{dx}{dt}\right)}^3}$

Aproximación al equilibrio

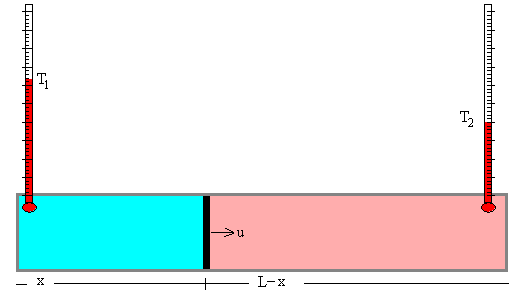
Ahora volvemos al estudio del sistema formado por los dos gases separados por un émbolo móvil

• T₁ es la temperatura del gas situado a la izquierda del émbolo

• T₂ es la temperatura del gas situado a la derecha del émbolo,

• x la posición del émbolo,

• S·x es el volumen del gas contenido en la parte izquierda  

• S·(L-x) el volumen del gas de la parte derecha del émbolo.

• Suponemos que el gas de la parte izquierda incrementa su volumen (dx/dt)>0, el gas de la parte derecha disminuye el volumen (dx/dt)<0

Variación de la temperatura

La ecuación para la variación de la temperatura T₁ del gas situado en la parte izquierda es

${\displaystyle c_v\frac{d{T}_1}{dt}=-\frac{R{T}_1}{x}\left(\frac{dx}{dt}\right)+\sqrt{\frac{8R{M}_g}{\pi }}\frac{\sqrt{T_1}}{x}{\left(\frac{dx}{dt}\right)}^2-\frac{M_g}{x}{\left(\frac{dx}{dt}\right)}^3}$

La ecuación para la variación de la temperatura T₂ del gas situado en la parte derecha es

${\displaystyle c_v\frac{d{T}_2}{dt}=\frac{R{T}_2}{L-x}\left(\frac{dx}{dt}\right)+\sqrt{\frac{8R{M}_g}{\pi }}\frac{\sqrt{T_2}}{L-x}{\left(\frac{dx}{dt}\right)}^2+\frac{M_g}{L-x}{\left(\frac{dx}{dt}\right)}^3}$

Ecuación del movimiento del émbolo

Como el sistema es aislado, la energía total permanece constante

${\displaystyle \frac{1}{2}M{\left(\frac{dx}{dt}\right)}^2+c_v{T}_1+c_v{T}_2=\text{cte}}$

El primer término es la energía cinética del émbolo de masa M. El segundo, la energía interna de un mol de gas contenido en la parte izquierda y el tercero, la energía interna de un mol de gas contenido en la parte derecha.

Derivamos con respecto del tiempo

${\displaystyle M\left(\frac{dx}{dt}\right)\left(\frac{d^{2}x}{d{t}^2}\right)+c_v\frac{d{T}_1}{dt}+c_v\frac{d{T}_2}{dt}=0}$

Despejamos la aceleración d²x/dt²

$$\begin{gathered} {\displaystyle \frac{d^{2}x}{d{t}^2}=\frac{R}{M}\left(\frac{T_1}{x}-\frac{T_2}{L-x}\right)-\frac{1}{M}\sqrt{\frac{8R{M}_g}{\pi }}\left(\frac{\sqrt{T_1}}{x}+\frac{\sqrt{T_2}}{L-x}\right)\left(\frac{dx}{dt}\right)+ \\ \frac{M_g}{M}\left(\frac{1}{x}-\frac{1}{L-x}\right){\left(\frac{dx}{dt}\right)}^2} \end{gathered}$$

En el caso general, se resuelve el sistema de dos ecuaciones diferenciales de primer orden y una ecuación de segundo orden con las condiciones iniciales siguientes: en el instante t=0,

• La posición del émbolo es x₀, su velocidad inicial es cero dx/dt=0

• La temperatura inicial del gas situado en la parte izquierda es T₁₀

• La temperatura inicial del gas situado en la parte derecha es T₂₀

En el estado final de equilibrio dx/dt=0, y d²x/dt²=0

${\displaystyle \frac{T_{1f}}{x_f}-\frac{T_{2f}}{L-x_f}=0}$

que corresponde a la igualdad de presiones p_1f=p_2f=p_f a un lado y otro del émbolo, tal como hemos visto en la introducción

Escalas

Antes de resolver numéricamente el sistema de tres ecuaciones diferenciales, es conveniente escribirlas en términos de las siguientes variables adimensionales

${\displaystyle \begin{array}{l}{\theta }_1=\frac{T_1}{T_{10}+T_{20}}{\theta }_2=\frac{T_2}{T_{10}+T_{20}}\gamma =\frac{c_p}{c_v}{c}_p=c_v+R\\ \xi =\frac{x}{L}\tau =\frac{t}{\sqrt{\frac{M{L}^2}{R(T_{10}+T_{20})}}}\delta =\sqrt{\frac{8M_g}{\pi M}}\end{array}}$

Las ecuaciones diferenciales se convierten en

${\displaystyle \begin{array}{l}\frac{d{\theta }_1}{d\tau }=-(\gamma -1)\frac{{\theta }_1}{\xi }\frac{d\xi }{d\tau }+\delta (\gamma -1)\frac{\sqrt{{\theta }_1}}{\xi }{\left(\frac{d\xi }{d\tau }\right)}^2-\frac{\pi }{8}(\gamma -1){\delta }^2\frac{1}{\xi }{\left(\frac{d\xi }{d\tau }\right)}^3\\ \frac{d{\theta }_2}{d\tau }=(\gamma -1)\frac{{\theta }_2}{1-\xi }\frac{d\xi }{d\tau }+\delta (\gamma -1)\frac{\sqrt{{\theta }_2}}{1-\xi }{\left(\frac{d\xi }{d\tau }\right)}^2+\frac{\pi }{8}(\gamma -1){\delta }^2\frac{1}{1-\xi }{\left(\frac{d\xi }{d\tau }\right)}^3\\ \frac{d^2\xi }{d{\tau }^2}=\frac{{\theta }_1}{\xi }-\frac{{\theta }_2}{1-\xi }-\delta \left(\frac{\sqrt{{\theta }_1}}{\xi }+\frac{\sqrt{{\theta }_2}}{1-\xi }\right)\frac{d\xi }{d\tau }+\frac{\pi }{8}{\delta }^2\left(\frac{1}{\xi }-\frac{1}{1-\xi }\right){\left(\frac{d\xi }{d\tau }\right)}^2\end{array}}$

Se resuelve el sistema de ecuaciones diferencias por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante τ=0, ξ=ξ₀, (dξ/dτ)₀=0,θ₁=θ₁₀, θ₂=1-θ₁₀

gamma=5.0/3;
delta=0.1;

%temperatura izquierda, temperatura derecha, posición émbolo, 
velocidad inicial
x0=[0.9,0.1,0.1,0];
fg=@(t,x) [-(gamma-1)*x(1)*x(4)/x(3)+delta*(gamma-1)*x(4)^2*sqrt(x(1))/x(3)-
(pi/8)*(gamma-1)*delta^2*x(4)^3/x(3); ...
    (gamma-1)*x(2)*x(4)/(1-x(3))+delta*(gamma-1)*x(4)^2*sqrt(x(2))/(1-x(3))+
(pi/8)*(gamma-1)*delta^2*x(4)^3/(1-x(3));...
    x(4);...
    x(1)/x(3)-x(2)/(1-x(3))-delta*x(4)*(sqrt(x(1))/x(3)+
sqrt(x(2))/(1-x(3)))+(pi/8)*delta^2*x(4)^2*(1/x(3)-1/(1-x(3)))];
tspan=[0 40];
[t,x]=ode45(fg,tspan,x0);
plot(t,x(:,3))
grid on
xlabel('t')
ylabel('x')
figure
subplot(2,1,1)
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('T_1')
subplot(2,1,2)
plot(t,x(:,2))
grid on
xlabel('t')
ylabel('T_2')

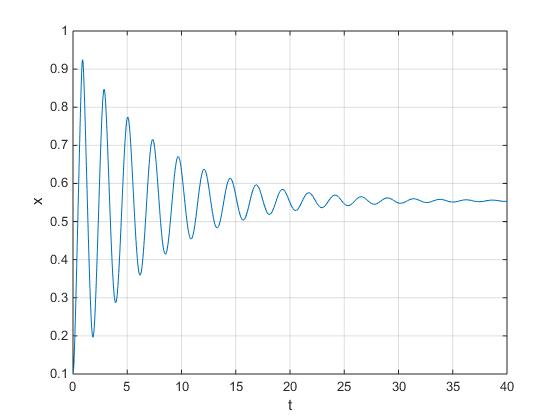
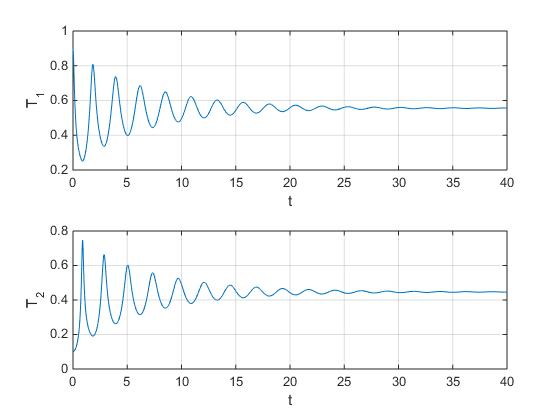
Posición del émbolo en función del tiempo

Temperaturas de los gases en función del tiempo

Se comprueba que se cumple la conservación de la energía expresada en términos de las variables adimensionales de la forma

${\displaystyle \frac{1}{2}(\gamma -1){\left(\frac{d\xi }{d\tau }\right)}^2+{\theta }_1+{\theta }_2=1}$

>> 0.5*(gamma-1)*x(:,4).^2+x(:,1)+x(:,2)
ans =
    1.0000
    1.0000
    1.0000
    1.0000
    1.0000
    .....

En el estado final, (dξ/dτ)=0 y (d²ξ/dτ²)=0 la relación entre las variables adimensionales serán:

• Conservación de la energía

θ_1f+θ_2f=1

• En la ecuación del movimiento del émbolo

${\displaystyle \frac{{\theta }_{1f}}{{\xi }_f}=\frac{{\theta }_{2f}}{1-{\xi }_f}}$

Equivalente a la igualdad de presiones a uno y otro lado del émbolo

Para un tiempo grande, cambiamos el valor de tspan=[0,100], la posición final del émbolo es ξ_f=0.5544, las temperaturas finales son θ_1f=0.5559 y θ_2f=0.4468, que como vemos cumple las relaciones anteriores.

El modelo cinético de gas ideal nos predice los valores finales de equilibrio de las temperaturas T_1f, T_2f y de los volúmenes V_1f=S·x_f,  V_2f=S·(L-x_f), mientras que la Termodinámica solamente nos dice que las presiones de los gases se deberán de igualar.

Caso particular

Cuando la masa M del émbolo es muy grande, el parámetro δ es casi cero. El sistema de tres ecuaciones diferenciales se simplifican notablemente. Las dos primeras se escriben

${\displaystyle \begin{array}{l}\frac{d{\theta }_1}{d\tau }=-(\gamma -1)\frac{{\theta }_1}{\xi }\frac{d\xi }{d\tau }\\ \frac{d{\theta }_2}{d\tau }=(\gamma -1)\frac{{\theta }_2}{1-\xi }\frac{d\xi }{d\tau }\end{array}}$

O bien,

${\displaystyle \begin{array}{l}\frac{d{\theta }_1}{{\theta }_1}=-(\gamma -1)\frac{d\xi }{\xi }\\ \frac{d{\theta }_2}{{\theta }_2}=(\gamma -1)\frac{d\xi }{1-\xi }\end{array}}$

Integramos ambas ecuaciones con las condiciones iniciales siguientes: en el instante inicial τ=0, las temperaturas iniciales de los recintos son θ₁₀, θ₂₀, la posición inicial del émbolo es ξ₀.

${\displaystyle \begin{array}{l}\frac{{\theta }_1}{{\theta }_{10}}={\left(\frac{{\xi }_0}{\xi }\right)}^{\gamma -1}\\ \frac{{\theta }_2}{{\theta }_{20}}={\left(\frac{1-{\xi }_0}{1-\xi }\right)}^{\gamma -1}\end{array}}$

Que corresponden a una transformación adiabática (TV^R/c_v) entre el estado inicial y final

${\displaystyle \begin{array}{l}{\theta }_{10}{\xi }_0^{\gamma -1}={\theta }_1{\xi }^{\gamma -1}\\ {\theta }_{20}{\left(1-{\xi }_0\right)}^{\gamma -1}={\theta }_2{\left(1-\xi \right)}^{\gamma -1}\end{array}}$

Donde γ-1=R/c_v.

La tercera ecuación diferencial nos describe el movimiento del émbolo

${\displaystyle \begin{array}{l}\frac{d^2\xi }{d{\tau }^2}=\frac{{\theta }_1}{\xi }-\frac{{\theta }_2}{1-\xi }\\ \frac{d^2\xi }{d{\tau }^2}=\frac{{\theta }_{10}{\xi }_0^{\gamma -1}}{{\xi }^{\gamma }}-\frac{{\theta }_{20}{\left(1-{\xi }_0\right)}^{\gamma -1}}{{\left(1-\xi \right)}^{\gamma }}\end{array}}$

gamma=5.0/3;
th10=0.9; %temperaturas
th20=0.1;
 
%posición émbolo, velocidad inicial
x0=[0.1,0];
fg=@(t,x) [x(2); th10*x0(1)^(gamma-1)/x(1)^gamma-
th20*(1-x0(1))^(gamma-1)/(1-x(1))^gamma];
tspan=[0 10];
[t,x]=ode45(fg,tspan,x0);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x')

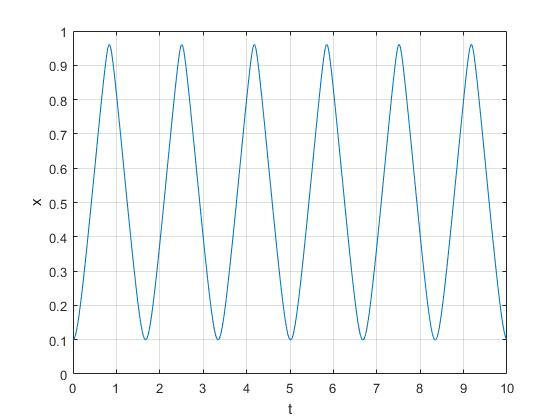
Experimenta oscilaciones sin rozamiento, la amplitud se mantiene constante. Por tanto, los términos de las tres ecuaciones diferenciales proporcionales a δ o a las potencias de δ son los responsables de llevar al émbolo a la la posición de equilibrio en reposo.

Actividades

Se introduce

• La posición inicial ξ₁₀ del gas situado en la parte izquierda del cilindro, en el control titulado Posición

• La temperatura adimensional inicial θ₁₀ del gas situado en la parte izquierda del cilindro, en el control titulado Temperatura 1

• La temperatura inicial del gas situado en la parte derecha del cilindro vale θ₂₀=1-θ₁₀

• El valor del parámetro δ, en el control titulado Parámetro

Se pulsa el botón titulado Nuevo

Observamos las oscilaciones del émbolo, hasta que al cabo de cierto tiempo alcanza la posición de equilibrio. Cuanto mayor sea el valor del parámetro δ, antes se alcanzará dicha posición.

Los termómetros marcan en cada instante las temperaturas adimensionales θ₁ y θ₂

En la parte superior, se representa la posición ξ del émbolo en función del tiempo adimensional τ.

En la parte superior derecha, se representa un diagrama en forma de tarta:

• en color azul, la energía interna del gas situado en la parte izquierda del cilindro, θ₁
• en color rojo, la energía interna del gas situado en la parte derecha, θ₂
• en color gris, la energía cinética del émbolo en términos de variables adimensionales

La suma de las tres clases de energía nos da la unidad. Si la suma difiere de la unidad quiere decir que el procedimiento numérico empleado en esta simulación no funciona adecuadamente.

Probar los siguientes ejemplos:

θ₁₀=0.9, ξ₀=0.1,δ=0.1
θ₁₀=0.7, ξ₀=0.4,δ=0.0
θ₁₀=0.9, ξ₀=0.1,δ=0.05

Referencias

Crosignani B., Di Porto P., Approach to thermal equilibrium in a system with adiabatic constraints. Am. J. Phys. 64 (5) May 1996, pp. 610-613