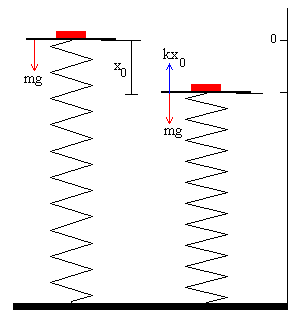
El bloque unido al muelle describirá un Movimiento Armónico Simple de frecuencia angular

${\displaystyle {\omega }^2=\frac{k}{m}}$

La posición de equilibrio se determina a partir de la condición de que la resultante de las fuerzas que actúan sobre el cuerpo sea nula.

La posiciónx₀ será tal que mg=kx₀

La ecuación del movimiento del sistema oscilante es

x=-x₀+A·sin(ω·t+φ)

Derivando con respecto del tiempo, obtenemos la expresión de la velocidad v.

v=dx/dt=Aω·cos(ω·t+φ)

En el instante t=0, el móvil se encuentra en la posición x=0 con velocidad nula v=0

Con estos datos determinamos la amplitud A y la fase inicial φ .

0=-x₀+A·sinφ
0=Aω·cosφ

la fase inicial es φ=π/2 y la amplitud A=x₀

La ecuación del movimiento es

x=-x₀+x₀·sin(ω·t+π/2) o bien,
x=x₀·(-1+cos(ωt))

Balance energético

El cuerpo está sometido a la acción de dos fuerzas conservativas, el peso cuya energía potencial es mgh y la fuerza que ejerce el muelle cuya energía potencial es kx²/2.

Ponemos el nivel cero de energía potencial gravitatoria en x=-x₀, en la posición de equilibrio.

En la situación de partida

• Energía cinética E_k=0
• Energía potencial elástica E_pe=0, el muelle se encuentra sin deformar
• Energía potencial gravitatoria E_p=mgx₀.

La energía total E=mgx₀, se va a distribuir entre las otras formas de energía sin que la suma total cambie.

Cuando el cuerpo pasa por la situación de equilibrio.

• Energía cinética E_k=mv²/2

• Energía potencial elástica E_pe=kx₀²/2, el muelle se ha deformado x₀

• Energía potencial gravitatoria E_p=0,

  ${\displaystyle E=\frac{1}{2}m{v}^2+\frac{1}{2}k{x}_0^2}$

Cuando el cuerpo pasa por la posición más baja x= -2x₀, la velocidad es cero,v=0

• Energía cinética E_k=0

• Energía potencial elástica E_pe=2kx₀², el muelle se ha deformado 2x₀

• Energía potencial gravitatoria E_p= -mgx₀, el cuerpo se encuentra x₀ por debajo del nivel cero de energía potencial

  ${\displaystyle E=-mg{x}_0+\frac{1}{2}k{(2x_0)}^2}$

Ejemplo:

Sea m=10 kg
Sea k=1000 N/m

El periodo de las oscilaciones es

${\displaystyle P=2\pi \sqrt{\frac{10}{1000}}=0.2\pi =0.63\text{s}}$

La posición de equilibrio es

1000·x₀=10·9.8, por lo que x₀=0.098 m=9.8 cm

La posición del cuerpo en función del tiempo es

x=9.8·(-1+cos(10t)) cm

A la derecha, vemos la representación de la posición x del cuerpo en función del tiempo t.

La energía total del cuerpo es E=-10·9.8·0.098=9.6 J

Actividades

Se introduce

• La constante elástica del muelle (N/m), en el control titulado Constante elástica
• La masa del cuerpo (kg), en el control titulado Masa del bloque

Se pulsa el botón titulado Nuevo, el programa verifica los datos introducidos y si son correctos, se pulsa ►.

Las tras clases de energías (cinética, potencial, potencial elástica) se representan mediante barras de colores. Observamos que la energía cinética y la energía potencial elástica son ambas positivas. Pero la energía potencial gravitatoria puede se positiva o negativa, ya que hemos puesto el nivel cero de energía potencial en la posición de equilibrio x₀. La suma de las tres clases de energías es constante.