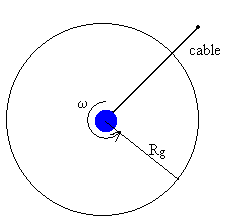
La Tierra tarda en dar una vuelta alrededor de su eje en 24 h, su velocidad angular de rotación es

${\displaystyle \omega =\frac{2\pi }{24·60·60}=7.272·{10}^{-5}\text{rad/s}}$

Un satélite artificial que describe una órbita circular con el mismo periodo que la rotación de la Tierra se denomina geoestacionario. Un observador situado en la línea que une el centro de la Tierra y el satélite lo vería inmóvil en la misma posición.

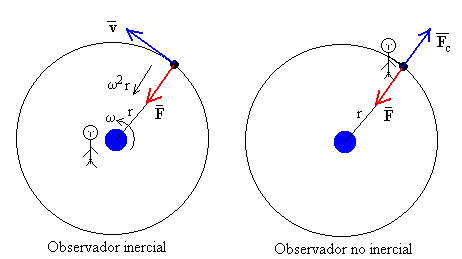
Si r es el radio de la órbita circular del satélite, aplicando la dinámica del movimiento circular uniforme, la masa del cuerpo m por la aceleración normal ω²r es igual a la fuerza F de atracción que ejerce la Tierra sobre el satélite.

${\displaystyle \begin{array}{l}m{\omega }^{2}r=G\frac{Mm}{r^2}{r}^3=\frac{GM}{{\omega }^2}\\ r^3=\frac{6.67·{10}^{-11}·5.98·{10}^{24}}{{\left(\frac{2\pi }{24·60·60}\right)}^2}r=42250\text{km}\end{array}}$

Desde el punto de vista del observador NO inercial, el astronauta que viaja en el satélite, éste se mantiene en equilibrio bajo la acción de la fuerza de atracción y la fuerza centrífuga.

Un cable que se eleva radialmente desde el ecuador.

Vamos a calcular las características que tiene que tener un cable (longitud y sección) hecho de un determinado material que se eleve radialmente desde un punto situado en el ecuador y que gira sincrónicamente con la Tierra, para que su peso se equilibre con la fuerza centrífuga.

La fuerza de atracción sobre cada elemento del cable decrece con el cuadrado de la distancia. Debido a la rotación del cable con velocidad angular ω, la fuerza centrífuga sobre un elemento del cable se incrementa linealmente con la distancia.

• Los elementos del cable situados por encima de la órbita geoestacionaria experimentan una fuerza de atracción menor que la fuerza centrífuga, la fuerza neta tiene dirección radial y es hacia afuera
• Los elementos del cable situados por debajo de la órbita geoestacionaria experimentan una fuerza de atracción mayor que la fuerza centrífuga, la fuerza neta tiene dirección radial y apunta hacia el centro de la Tierra.

Si el cable fuese suficientemente largo, cuyo extremo esté bien por encima de la órbita geoestacionaria, el peso del cable se podría equilibrar con la fuerza centrífuga.

Vamos a estudiar dos situaciones: un cable de sección constante y un cable de sección variable, veremos las ventajas de esta último.

Cable de sección constante

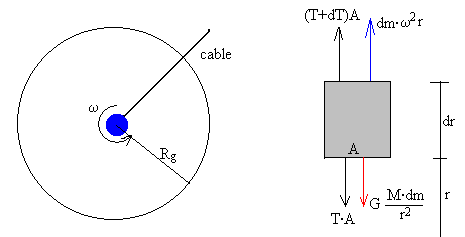
Las fuerzas sobre un elemento de cable de masa dm situado a una distancia r del centro de la Tierra son

• La fuerza de atracción de la Tierra, $G\frac{M·dm}{r^2}$

• La fuerza centrífuga, dm·ω²r

• La fuerza que ejerce la parte inferior del cable sobre el elemento, T·A, donde T es el esfuerzo (fuerza por unidad de área)

• La fuerza que ejerce la parte superior del cable sobre dicho elemento, (T+dT)A

La masa dm del elemento de cable de longitud dr es ρAdr. Siendo ρ la densidad del material del que está hecho el cable.

${\displaystyle \begin{array}{l}(T+dT)A+dm·{\omega }^{2}r=TA+G\frac{M·dm}{r^2}\\ dT=\rho \left(G\frac{M}{r^2}-{\omega }^{2}r\right)dr\\ {\displaystyle \underset{0}{\overset{T}{\int }}dT={\displaystyle \underset{R}{\overset{r}{\int }}\rho \left(G\frac{M}{r^2}-{\omega }^{2}r\right)dr}}\\ T=\rho \left(G\frac{M}{R}+{\omega }^2\frac{R^2}{2}-G\frac{M}{r}-{\omega }^2\frac{r^2}{2}\right)\\ T=\rho R^{2}g\left(\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{1}{r}-\frac{r^2}{2R_g^3}\right)\end{array}}$

g es la aceleración de la gravedad en la superficie de la Tierra g=GM/R² y R_g es el radio de la órbita geoestacionaria.

${\displaystyle R_g^3=\frac{GM}{{\omega }^2}=\frac{g{R}^2}{{\omega }^2}}$

G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
Rg=(G*M/(2*pi/(24*3600))^2)^(1/3); %radio de la órbita geoestacionaria
r=(1:0.2:25)*R;
T=(1/R+R^2/(2*Rg^3)-1./r-r.^2/(2*Rg^3))/(1/R+R^2/(2*Rg^3)-3/(2*Rg));
plot(r/1000,T)
xlabel('r(km)')
ylabel('T/T_g')
title('Tensión de un cable de sección uniforme')

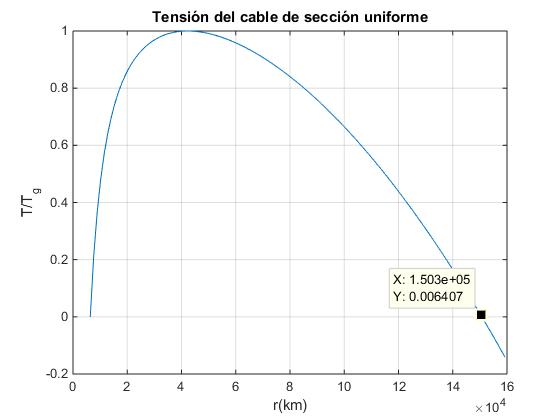
El esfuerzo T se hace máximo, para una distancia r al centro de la Tierra tal que dT/dr=0

${\displaystyle G\frac{M}{r^2}-{\omega }^{2}r=0}$

Es decir cuando r=R_g, el radio de la órbita geoestacionaria. El valor del esfuerzo en esta posición es

${\displaystyle T=\rho R^{2}g\left(\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{3}{2R_g}\right)}$

El esfuerzo T se hace cero para una distancia r al centro de la Tierra que es la raíz de una ecuación cúbica. Una de las raíces es r=R, calculamos la otra raíz

${\displaystyle \begin{array}{l}\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{1}{r}-\frac{r^2}{2R_g^3}=0\\ r^3-\left(2\frac{R_g^3}{R}+R^2\right)r+2R_g^3=0\\ (r-R)\left(r^2+rR-2\frac{R_g^3}{R}\right)=0\\ r=\frac{R}{2}\left(\sqrt{1+8\frac{R_g^3}{R^3}}-1\right)\end{array}}$

El radio de la Tierra es R=6370 km y el radio de la órbita geoestacionaria es R_g=42 250 km, obtenemos r=150 732 km, tal como vemos en la gráfica

La longitud del cable es H=r-R=144 362 km

Cable de sección variable

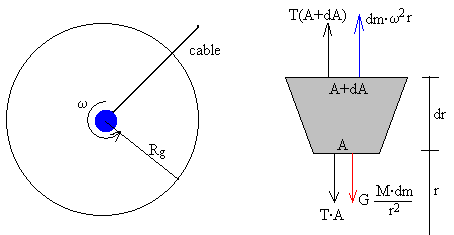
El cable experimentará un esfuerzo T (fuerza por unidad de área) constante en todos sus puntos.

Las fuerzas sobre un elemento de cable de masa dm situado a una distancia r del centro de la Tierra son:

• La fuerza de atracción de la Tierra, $G\frac{M·dm}{r^2}$

• La fuerza centrífuga, dm·ω²r

• La fuerza que ejerce la parte inferior del cable sobre el elemento, T·A

• La fuerza que ejerce la parte superior del cable sobre dicho elemento, T(A+dA)

La masa dm del elemento de cable de longitud dr es ρAdr. Siendo ρ la densidad del material del que está hecho el cable.

Si el elemento está en equilibrio, tendremos

${\displaystyle \begin{array}{l}T(A+dA)+dm·{\omega }^{2}r=TA+G\frac{M·dm}{r^2}\\ \frac{dA}{A}=\frac{\rho }{T}\left(G\frac{M}{r^2}-{\omega }^{2}r\right)dr\\ {\displaystyle \underset{A_s}{\overset{A}{\int }}\frac{dA}{A}={\displaystyle \underset{R}{\overset{r}{\int }}\frac{\rho }{T}\left(G\frac{M}{r^2}-{\omega }^{2}r\right)dr}}\\ A=A_s\exp \left(\frac{\rho }{T}\left(G\frac{M}{R}+{\omega }^2\frac{R^2}{2}-G\frac{M}{r}-{\omega }^2\frac{r^2}{2}\right)\right)\\ A=A_s\exp \left(\frac{\rho g{R}^2}{T}\left(\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{1}{r}-\frac{r^2}{2R_g^3}\right)\right)\end{array}}$

Donde A_s es la sección del cable en la superficie de la Tierra r=R, g es la aceleración de la gravedad en la superficie de la Tierra g=GM/R² y R_g es el radio de la órbita geoestacionaria.

La sección del cable A toma un valor máximo para una distancia al centro r tal que dA/dr=0. El máximo de la función exponencial equivale al máximo del argumento

${\displaystyle \frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{1}{r}-\frac{r^2}{2R_g^3}}$

derivando con respecto a r, e igualando a cero

${\displaystyle \frac{1}{r^2}-\frac{2r}{2R_g^3}=0r=R_g}$

La sección del cable en la órbita geoestacionaria r=R_g vale

${\displaystyle A_g=A_s\exp \left(\frac{\rho g{R}^2}{T}\left(\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{3}{2R_g}\right)\right)}$

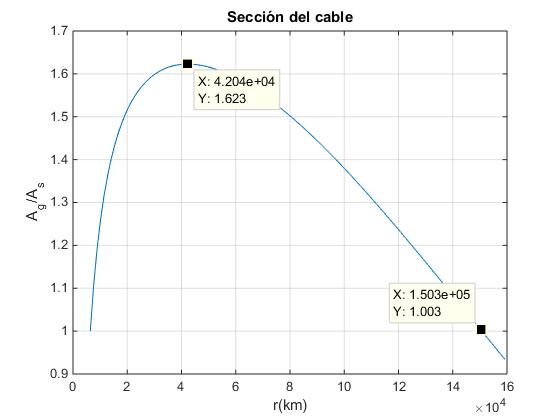
Calculamos el cociente A_g/A_s para distintos materiales

Solamente con un material de baja densidad ρ y con un alto valor de esfuerzo máximo T se pueden alcanzar cocientes A_g/A_s razonables para la construcción de dicho cable.

La sección del cable es máxima en la órbita geoestacionaria, después disminuye y se vuelve a hacer igual a A_s a la distancia r del centro

${\displaystyle \begin{array}{l}{A}_s=A_s\exp \left(\frac{\rho g{R}^2}{T}\left(\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{1}{r}-\frac{r^2}{2R_g^3}\right)\right)\\ \frac{\rho g{R}^2}{T}\left(\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{1}{r}-\frac{r^2}{2R_g^3}\right)=0\end{array}}$

Como en el apartado anterior, dicha distancia es la raíz de una ecuación cúbica. Una de las raíces es r=R, y al otra raíz es

${\displaystyle r=\frac{R}{2}\left(\sqrt{1+8\frac{R_g^3}{R^3}}-1\right)}$

El radio de la Tierra es R=6370 km y el radio de la órbita geoestacionaria es R_g=42 250 km, obtenemos r=150 732 km. La longitud del cable es H=r-R=144 362 km

Representamos el área de la sección del cable con la distancia r.

Vamos a cambiar el cociente densidad/esfuerzo máximo tomando como referencia el material Carbono nanotubos

${\displaystyle k\frac{1300}{130·{10}^9}}$

Si el factor k fuese uno, la situación más favorable, la sección del cable en la órbita geoestacionaria sería A_g/A_s=1.623, valor mínimo esperable si se pudiese producir en el futuro este material en grandes cantidades. Si por razones de seguridad el esfuerzo máximo se reduce a la mitad, T=65·10⁹ N/m², una situación algo más realista, el factor tomaría el valor k=2. El área de la sección del cable A_g en la órbita geoestacionaria sería mayor.

Por ejemplo, si la densidad del material fuese ρ=1500 kg/m³ y el máximo esfuerzo admisible fuese de T=50·10⁹ N/m² el factor k para este hipotético material valdría

${\displaystyle \frac{1500}{50·{10}^9}=k\frac{1300}{130·{10}^9}k=3}$

Este pequeño programa nos muestra que un pequeño incremento del cociente densidad/esfuerzo máximo ρ/T equivale a un aumento muy grande del cociente A_g/A_s, ya que dicho cociente entra como argumento de una exponencial.

G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
Rg=(G*M/(2*pi/(24*3600))^2)^(1/3); %radio de la órbita geoestacionaria
k=1; %factor
r=(1:0.2:25)*R;
y=exp(k*1300*9.8*R*R*(1/R+R^2/(2*Rg^3)-1./r-r.^2/(2*Rg^3))/130.0e9);
plot(r/1000,y)
grid on
xlabel('r(km)')
ylabel('A_g/A_s')
title('Sección del cable')

Contrapeso

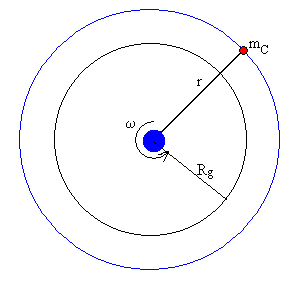
Se puede reducir la longitud del cable, poniendo un contrapeso en su extremo superior. La distancia al centro de la Tierra del contrapeso será  r>R_g. El contrapeso experimenta una fuerza centrífuga mayor que la fuerza de atracción.

El contrapeso describe una órbita circular de radio r, bajo la acción de la fuerza de atracción y la fuerza que ejerce el cable. O desde el punto de vista del observador no inercial que viaja con el contrapeso, la fuerza de atracción y la acción del cable se equilibran con la fuerza centrífuga

${\displaystyle \begin{array}{l}\frac{GM{m}_c}{r^2}+A(r)T=m_c{\omega }^{2}r\\ \frac{GM{m}_c}{r^2}+T·A_s\exp \left(\frac{\rho g{R}^2}{T}\left(\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{1}{r}-\frac{r^2}{2R_g^3}\right)\right)=m_c{\omega }^{2}r\\ m_c=\frac{T·A_s}{R^{2}g}\frac{\exp \left(\frac{\rho g{R}^2}{T}\left(\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{1}{r}-\frac{r^2}{2R_g^3}\right)\right)}{\frac{r}{R_g^3}-\frac{1}{r^2}}\end{array}}$

Cuando r→R_g la masa del contrapeso m_c→∞

La masa total del cable se calcula mediante la integral

${\displaystyle m_E=\rho {\displaystyle \underset{R}{\overset{r}{\int }}A(r)·dr}}$

La integral definida se calcula empleando procedimientos numéricos.

Ejemplo:

Sea la densidad del hipotético material del que está hecho el cable ρ=1500 kg/m³ y el máximo esfuerzo admisible T=50·10⁹ N/m². Supongamos que el área de la sección del cable en la superficie de la Tierra A_s=1.5·10^-7 m², que equivale a una cable de sección circular de 0.22 mm de radio y situamos el contrapeso en r=100 000 km

La masa del contrapeso sería m_C=37 368.5 kg, y la masa del cable m_E=74 882.6 kg

G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
Rg=(G*M/(2*pi/(24*3600))^2)^(1/3); %radio de la órbita geoestacionaria
rho=1500; %densidad
T=50e9; %tensión del cable
As=1.5e-7; %sección del cable en sperficie de la Tierra
rm=100e6; %posición del contrapeso
f= @(r) exp(rho*9.8*R*R*(1/R+R^2/(2*Rg^3)-1./r-r.^2/(2*Rg^3))/T);
masa=quad(f,R,rm)*rho*As;
mC=T*As*f(rm)/(R^2*9.8*(rm/Rg^3-1/rm^2))
fprintf('Masa del cable %5.1f, contrapeso %5.1f (kg)\n',masa, mC)

Masa del cable 74883.4, contrapeso 40416.8 (kg)

Aplicaciones

Subir o bajar cargas al espacio

El cable se puede utilizar para subir y bajar cargas a grandes distancias. Sería como un “puente hacia las estrellas”. Cuando deslizamos un cuerpo a lo largo del cable hemos de tener en cuenta que si su distancia r al centro de la Tierra es:

• r<R_g, la fuerza de atracción supera la fuerza centrífuga, el cuerpo desliza hacia la Tierra.
• r>R_g, la fuerza centrífuga supera la fuerza de atracción, el cuerpo se aleja radialmente de la Tierra.
• En la posición r=R_g, el cuerpo está en una posición de equilibrio inestable.

Solamente hemos de suministrar energía para elevar el cuerpo desde la superficie de la Tierra hasta la órbita geoestacionaria, después no es necesario suministrar ninguna energía al cuerpo que asciende por el cable.

Supongamos que un cuerpo de masa m desliza por el cable desde la superficie de la Tierra hasta una distancia r de su centro. El trabajo realizado por la fuerza centrífuga es

${\displaystyle W_1={\displaystyle \underset{R}{\overset{r}{\int }}m{\omega }^{2}r·dr=\frac{1}{2}}m{\omega }^2\left(r^2-R^2\right)}$

es un trabajo positivo, puesto que la fuerza y el desplazamiento tienen el mismo sentido

El trabajo realizado por la fuerza de atracción es

${\displaystyle W_2={\displaystyle \underset{R}{\overset{r}{\int }}-G\frac{Mm}{r^2}dr=G}\frac{Mm}{r}-G\frac{Mm}{R}}$

es un trabajo negativo, puesto que la fuerza y el desplazamiento tienen sentidos contrarios.

Para elevar una carga desde la superficie de la Tierra hasta una  distancia r de su centro es necesario suministrar la energía por unidad de masa

${\displaystyle \frac{E}{m}=-\frac{(W_1+W_2)}{m}=g{R}^2\left(\frac{1}{R}+\frac{R^2}{2R_g^3}-\frac{1}{r}-\frac{r^2}{2R_g^3}\right)}$

Esta expresión aparece en el exponente de la fórmula que nos proporciona el área de la sección del cable con la distancia radial r.

G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
Rg=(G*M/(2*pi/(24*3600))^2)^(1/3); %radio de la órbita geoestacionaria
r=(1:0.2:25)*R;
 %energía por unidad de masa
E=9.8*R^2*(1/R+R^2/(2*Rg^3)-1./r-r.^2/(2*Rg^3));
plot(r/1000,E)
grid on
xlabel('r(km)')
ylabel('E/m')
title('Energía')

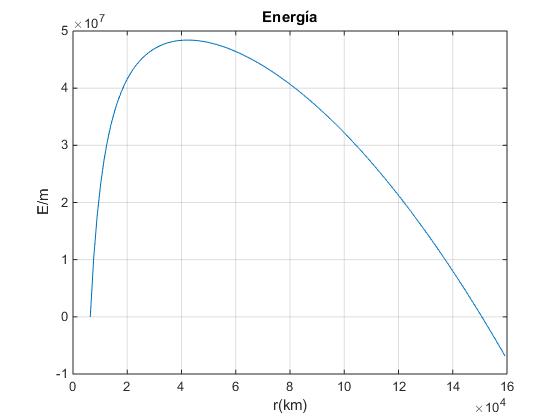
El máximo de E/m aparece en la órbita geoestacionaria. Es energéticamente más rentable elevar cargas a mayor distancia. La energía se hace cero para la distancia al centro de la Tierra r=150 732 km, que ya hemos calculado anteriormente, podemos por tanto, elevar una carga a esta posición sin consumo de energía, gracias al movimiento de rotación de la Tierra. Más allá de este punto podemos producir incluso energía.

Lanzamiento desde el extremo del cable

G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
M=5.98e24; %masa de la Tierra
w=2*pi/(24*3600); %velocidad angular de rotación de la Tierra
r=(1:0.2:25)*R;
Ek=w^2*r.^2/2; %energía cinética
Ep=-G*M./r;  %energía potencial
E=Ep+Ek;     %energía total
%representa la energía en megajulios 10^6 J
plot(r/1000,Ek/1e6,r/1000,Ep/1e6,r/1000,E/1e6)
legend('E_k','E_p','E', 'location','northwest')
grid on
xlabel('r(km)')
ylabel('E/m (MJ)')
title('Energía')

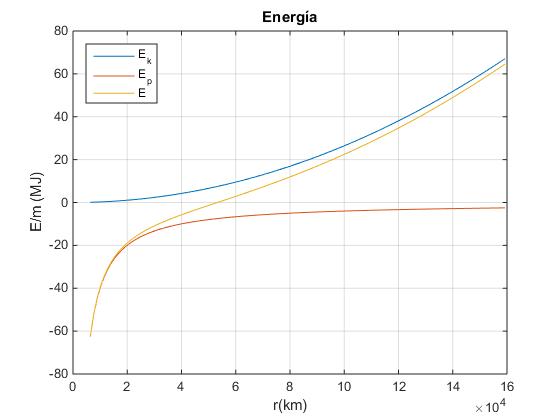
En la gráfica se ha representado la energía cinética, potencial y la energía total de un cuerpo de masa m situado sobre el cable a una distancia r del centro de la Tierra.

Para una cierta posición r_e la energía cinética del cuerpo que asciende a lo largo del cable se hace igual a la energía potencial, la energía total es cero, el cuerpo alcanza la velocidad de escape

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{\left(\omega r\right)}^2-G\frac{Mm}{r}=0\\ r^3=\frac{2GM}{{\omega }^2}=2R_g^3{r}_e=\sqrt[3]{2}{R}_g\end{array}}$

El cable tiene que tener una longitud mayor que H=r_e-R=46 862 km para que pueda ser utilizado con el propósito de lanzar naves espaciales a otros planetas.

Para que sirva de comparación mencionaremos, que la energía de un cuerpo situado sobre la superficie de la Tierra es

${\displaystyle E=\frac{1}{2}m{\omega }^2{R}^2-G\frac{Mm}{R}=0.11·{10}^{6}m-62.62·{10}^{6}m=-62.51·{10}^{6}m\text{J}}$

Por tanto, para lanzar un cuerpo al espacio exterior liberándose de la atracción de la Tierra necesitamos invertir un mínimo de 62.5 MJ/kg de energía.

Supongamos que lanzamos una nave espacial desde el extremo del cable a una distancia r₀>r_e del centro de la Tierra. Después de ser soltado, la nave espacial se aleja de la Tierra siguiendo una órbita elíptica en uno de cuyos focos se encuentra el Sol.

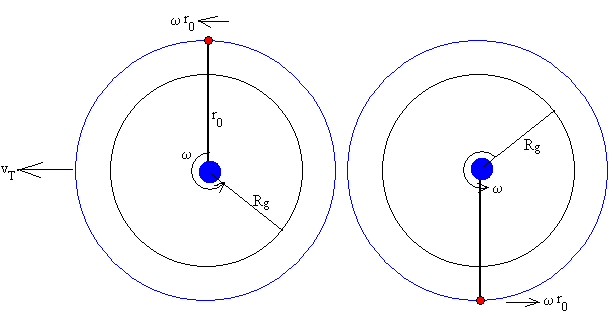
Sea  v_T la velocidad de traslación de la Tierra alrededor del Sol y ωr₀ la velocidad de la nave espacial que se suelta del extremo del cable. Supongamos que se suelta la nave cuando ambas velocidades tienen la misma dirección y sentido (figura de la izquierda), por lo que la velocidad de la nave espacial respecto del Sol sería v_T+ωr₀.

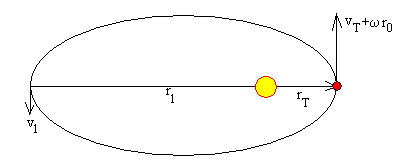
Sea r_T la distancia entre la Tierra y el Sol y M_s la masa del Sol. Aplicando la constancia del momento angular y de la energía total (la fuerza de atracción del Sol sobre la nave espacial es central y conservativa) tenemos un sistema de dos ecuaciones con dos incógnitas, de las cuales despejamos las incógnitas r₁ y v₁

${\displaystyle \begin{array}{l}m{r}_T(v_T+\omega r_0)=m{r}_1{v}_1\\ \frac{1}{2}m{\left(v_T+\omega r_0\right)}^2-G\frac{M_{s}m}{r_T}=\frac{1}{2}m{v}_1^2-G\frac{M_{s}m}{r_1}\\ r_1=\frac{r_T^2{\left(v_T+\omega r_0\right)}^2}{2G{M}_s-r_T{\left(v_T+\omega r_0\right)}^2}\end{array}}$

Ejemplo.

La Tierra describe una órbita aproximadamente circular alrededor del Sol de radio r_T=149.6·10⁶ km=1 UA. Aplicando la dinámica del movimiento circular uniforme, calculamos la velocidad v_T de traslación de la Tierra alrededor del Sol. La masa del Sol es M_s= 1.98·10³⁰ kg

${\displaystyle \begin{array}{l}m\frac{v_T^2}{r_T}=G\frac{M_{s}m}{r_T^2}\\ v_T=\sqrt{\frac{G{M}_s}{r_T}}=\sqrt{\frac{6.67·{10}^{-11}·1.98·{10}^{30}}{149.6·{10}^9}}=29712\text{m/s}\end{array}}$

Supongamos que la distancia del punto de lanzamiento situado en el extremo del cable al centro de la Tierra es r₀=107 000 km, y que la velocidad de traslación de la Tierra v_T  alrededor del Sol y la velocidad de la nave espacial ωr₀  en el momento del lanzamiento, tienen la misma dirección y sentido

La máxima distancia de alejamiento de la nave espacial (afelio) es r₁=5.84·10¹¹ m=3.906 UA, no llega a la órbita de Júpiter 5.203 UA

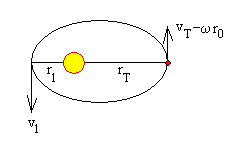
Supongamos ahora, que la velocidad de la Tierra v_T  y la velocidad de la nave espacial ωr₀  tienen la misma dirección y sentido contrario

Entonces, el punto del lanzamiento será el afelio, la distancia de mínimo alejamiento de la nave espacial al Sol (perihelio) será

${\displaystyle r_1=\frac{r_T^2{\left(v_T-\omega r_0\right)}^2}{2G{M}_s-r_T{\left(v_T-\omega r_0\right)}^2}}$

Con los datos anteriores r₁=0.56·10¹¹ m=0.374 UA, llega hasta la órbita de Mercurio 0.387 UA.

Actividades

El cable por el cual van a ascender las naves espaciales que se van a lanzar al espacio tiene 150 000 km.

El punto del lanzamiento se puede cambiar introduciendo una distancia mayor que 53233 km que es la posición que corresponde a una energía aproximadamente nula de la nave espacial.

Se pulsa el botón titulado Nuevo y a continuación, ►

Observamos la Tierra muy pequeña de color azul y un largo cable girando  sincrónicamente con la Tierra. La circunferencia de color azul corresponde a la órbita geoestacionaria.

• Una flecha de color rojo, nos muestra la velocidad de la nave espacial en el momento del lanzamiento.
• La flecha de color azul corresponde a la velocidad de traslación de la Tierra en su órbita circular alrededor del Sol.

Cuando los dos vectores tienen la misma dirección y sentido, la nave espacial se aleja más del Sol. Cuando tienen sentidos opuestos el alejamiento es mínimo.

Pulsamos el botón Lanzar

Observamos el movimiento de la Tierra alrededor del Sol y el movimiento de la nave espacial describiendo una órbita elíptica uno de cuyos focos es el Sol.

El eje horizontal está dividido en intervalos iguales de 1 UA=149.6·10⁹ m

Referencias

Aravind P. K. The physics of the space elevator. Am. J. Phys. 75 (2) February 2007, pp. 125-130

Artukovic R. The space elevator. www.zadar.net/space-elevator/