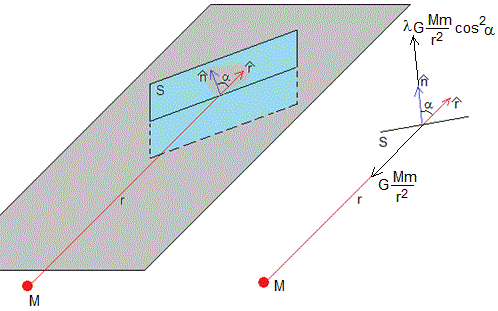
En la página titulada, el efecto de la radiación electromagnética sobre el movimiento de los cuerpos se explica que una vela solar está sometida a dos fuerzas:

• La fuerza repulsiva que ejerce la presión de la radiación solar sobre la superficie plana de la vela, cuya dirección es perpendicular a la vela.

${\displaystyle \overrightarrow{\frac{F_n}{m}}=\lambda \frac{GM}{r^2}{\cos }^2\alpha ·\widehat{n}}$

Donde λ es un parámetro (lightness number) que depende de la vela y la radiación solar

• La fuerza atractiva que ejerce el Sol sobre la vela, cuya dirección es radial

${\displaystyle \overrightarrow{\frac{F_r}{m}}=-\frac{GM}{r^2}\widehat{r}}$

La vela es perpendicular a la dirección radial

La situación más simple se produce cuando el ángulo α=0. El efecto neto de la radiación solar es el de disminuir la aceleración de la gravedad local GM/r²

${\displaystyle \overrightarrow{F}=-\frac{GMm}{r^2}(1-\lambda )\widehat{r}}$

Se trata de una fuerza central y conservativa, su energía potencial es

${\displaystyle E_p=-\frac{GMm}{r}(1-\lambda )}$

La nave espacial con la vela desplegada describe una trayectoria que es una cónica que en coordenadas polares, basta sustituir GMm por GMm(1-λ)

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }\epsilon =\sqrt{1+\frac{2L^{2}E}{m^3{\left((1-\lambda )GM\right)}^2}}d=\frac{L^2}{(1-\lambda )GM{m}^2}}$

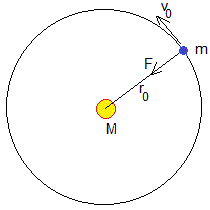
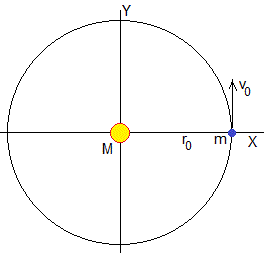
Consideremos una nave espacial de masa m que describe una órbita circular de radio r₀ alrededor del Sol (masa M)

Aplicamos la ecuación de la dinámica del movimiento circular uniforme.

${\displaystyle G\frac{Mm}{r_0^2}=m\frac{v_0^2}{r_0},v_0=\sqrt{\frac{GM}{r_0}}}$

La energía de la nave espacial es

${\displaystyle E_0=\frac{1}{2}m{v}_0^2-G\frac{Mm}{r_0}=\frac{1}{2}G\frac{Mm}{r_0}}$

En un momento dado la nave espacial despliega una vela plana perpendicular a la dirección radial de parámetro λ. La energía y el momento angular es

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}_0^2-G\frac{Mm}{r_0}(1-\lambda )=\frac{1}{2}G\frac{Mm}{r_0}-G\frac{Mm}{r_0}(1-\lambda )=G\frac{Mm}{r_0}\left(\lambda -\frac{1}{2}\right)\\ L=m{r}_0{v}_0=m\sqrt{GM{r}_0}\end{array}}$

Los parámetros d y ε (excentricidad) de su trayectoria valen

${\displaystyle \begin{array}{l}d=\frac{L^2}{(1-\lambda )GM{m}^2}=\frac{1}{1-\lambda }{r}_0\\ \epsilon =\sqrt{1+\frac{2L^{2}E}{m^3{\left((1-\lambda )GM\right)}^2}}=\sqrt{1+\frac{2m^{2}GM{r}_{0}G\frac{Mm}{r_0}\left(\lambda -\frac{1}{2}\right)}{m^3{\left((1-\lambda )GM\right)}^2}}=\sqrt{1+\frac{\left(2\lambda -1\right)}{{\left(1-\lambda \right)}^2}}=\frac{\lambda }{1-\lambda }\end{array}}$

La ecuación de la trayectoria es una cónica (elipse, parábola o hipérbola) dependiendo del valor del parámetro λ .

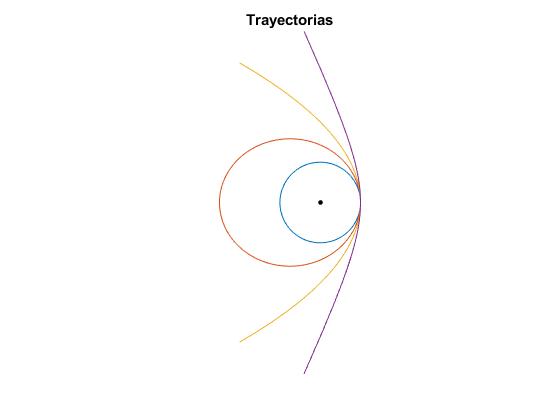
Sea una nave espacial que describe una órbita circular de r₀=1.496·10¹¹ m, alrededor del Sol, la misma que la Tierra. En un momento dado despliega la vela, vamos a representar la trayectoria que sigue para λ=0.3, 0.5 y 0.7

r0=1; %una UA=1.496e11 m
hold on
fplot(@(x) cos(x), @(x) sin(x),[0,2*pi]); %órbita circular
for lambda=[0.3,0.5,0.7]
    d=r0/(1-lambda);
    ex=lambda/(1-lambda);%excentricidad
    f=@(x) d./(1+ex*cos(x));
    ang=pi; %elipse
    if ex>1 %hipérbola
        ang=acos(-1/ex)-20*pi/180; 
    elseif ex==1 %parábola
        ang=2*pi/3;
    end
    fplot(@(x) f(x).*cos(x), @(x) f(x).*sin(x) ,[-ang,ang])
end
plot(0,0,'ko','markersize',3,'markeredgecolor','k','markerfacecolor','k')
hold off
axis equal
axis off
xlabel('x')
ylabel('y')
grid on
title('Trayectorias')

Solución numérica

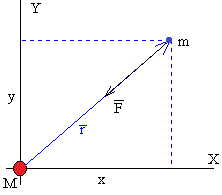
En la página titulada Solución numérica de las ecuaciones del movimiento, las componentes de la aceleración de la nave espacial con la vela desplegada son

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-G\frac{M}{r^2}(1-\lambda )\frac{x}{r}\hfill \\ \frac{d^{2}y}{d{t}^2}=-G\frac{M}{r^2}(1-\lambda )\frac{y}{r}\hfill \end{array}}$

Antes de resolver el sistema de ecuaciones diferenciales por procedimientos numéricos, es conveniente prepararlas para que el ordenador no maneje números excesivamente grandes o pequeños.

Establecemos un sistema de unidades en el que la longitud se mide en unidades r₀=1.496·10¹¹ m y el tiempo en unidades P=2πr₀/v₀, el tiempo que tarda en dar una vuelta completa

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-G\frac{M}{r^2}(1-\lambda )\frac{x}{r}\\ \frac{d^{2}X}{d{\tau }^2}\frac{r_0}{P^2}=-GM\frac{X}{{\left(X^2+Y^2\right)}^{3/2}}(1-\lambda )\frac{1}{r_0^2}\\ \frac{d^{2}X}{d{\tau }^2}=-4{\pi }^2(1-\lambda )\frac{X}{{\left(X^2+Y^2\right)}^{3/2}}\end{array}}$

Lo mismo para la ecuación diferencial en y. Resolvemos el sistema de ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^{2}X}{d{\tau }^2}=-4{\pi }^2(1-\lambda )\frac{X}{{\left(X^2+Y^2\right)}^{3/2}}\\ \frac{d^{2}Y}{d{\tau }^2}=-4{\pi }^2(1-\lambda )\frac{Y}{{\left(X^2+Y^2\right)}^{3/2}}\end{array}}$

Con las condiciones iniciales siguientes: en el instante τ=0, parte de la posición X=1, Y=0, con velocidad inicial, dX/dτ=0, dY/dτ=v₀(P/r₀)=2π

Definimos una función denominada stop_nave para detener el proceso de integración cuando complete un periodo, es decir, cuando la ordenada Y que en el código es x(3) sea cero (stopin=1) y sea una función creciente (direction=1).

function vela_solar_1
    lambda=0.4; %parámetro lambda
    fg=@(t,x)[x(2);-4*pi^2*(1-lambda)*x(1)/(sqrt(x(1)^2+x(3)^2))^3; x(4);
-4*pi^2*(1-lambda)*x(3)/(sqrt(x(1)^2+x(3)^2))^3];
    opts=odeset('events',@stop_nave);
    [~,x]=ode45(fg,[0,10],[1,0,0,2*pi], opts);
    hold on
    fplot(@(x) cos(x), @(x) sin(x),[0,2*pi]);
    plot(x(:,1),x(:,3),'r') %órbita elíptica
    plot(0,0,'ko','markersize',3,'markeredgecolor','k','markerfacecolor','k')
    hold off
    axis equal
    xlabel('x')
    ylabel('y')
    grid on
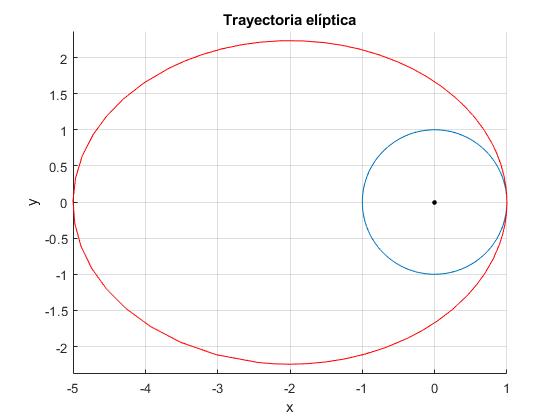
    title('Trayectoria elíptica')

    function [detect,stopin,direction]=stop_nave(~,x)
        detect=x(3); 
        stopin=1; 
        direction=1; 
    end
end

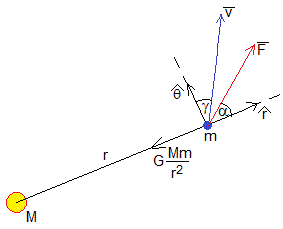
La normal a la vela plana forma un ángulo α con la dirección radial

En la página titulada Viaje de la Tierra a Marte siguiendo una trayectoria en forma de espiral logarítmica, estudiamos la trayectoria en forma de espiral logarítmica que sigue una nave espacial cuyos motores proporcionan una fuerza de empuje inversamente proporcional a la distancia al Sol, tangente a la trayectoria

En esta ocasión, la fuerza de empuje F (inversamente proporcional al cuadrado de la distancia) no es tangente a la trayectoria, sino que forma un ángulo α con la dirección radial. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=-G\frac{Mm}{r^2}+\lambda G\frac{Mm}{r^2}{\cos }^3\alpha \hfill \\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)=\lambda G\frac{Mm}{r^2}{\cos }^2\alpha \sin \alpha \hfill \end{array}}$

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r=r_0\exp (\tan \gamma ·\theta )}$

Velocidad de la nave espacial

Derivamos dos veces r respecto del tiempo t

${\displaystyle \begin{array}{l}\frac{dr}{dt}=\tan \gamma ·r\frac{d\theta }{dt}\\ \frac{d^{2}r}{d{t}^2}=\tan \gamma ·r\frac{d^2\theta }{d{t}^2}+{\tan }^2\gamma ·r{\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

Sustituimos en la primera ecuación diferencial

${\displaystyle \begin{array}{l}\tan \gamma ·r\frac{d^2\theta }{d{t}^2}+{\tan }^2\gamma ·r{\left(\frac{d\theta }{dt}\right)}^2-r{\left(\frac{d\theta }{dt}\right)}^2=-G\frac{M}{r^2}\left(1-\lambda {\cos }^3\alpha \right)\hfill \\ r\frac{d^2\theta }{d{t}^2}=-G\frac{M}{r^2}\frac{1-\lambda {\cos }^3\alpha }{\tan \gamma }+\frac{r}{\tan \gamma }{\left(\frac{d\theta }{dt}\right)}^2-\tan \gamma ·r{\left(\frac{d\theta }{dt}\right)}^2\hfill \end{array}}$

Sustituimos en la segunda ecuación diferencial, rd²θ/dt² y dr/dt llegando a

${\displaystyle \begin{array}{l}-G\frac{M}{r^2}\frac{1-\lambda {\cos }^3\alpha }{\tan \gamma }+\frac{r}{\tan \gamma }{\left(\frac{d\theta }{dt}\right)}^2-\tan \gamma ·r{\left(\frac{d\theta }{dt}\right)}^2+2\tan \gamma ·r{\left(\frac{d\theta }{dt}\right)}^2=\lambda G\frac{M}{r^2}{\cos }^2\alpha \sin \alpha \\ -G\frac{M}{r^2}\frac{1-\lambda {\cos }^3\alpha }{\tan \gamma }+\frac{r}{\cos \gamma ·\sin \gamma }{\left(\frac{d\theta }{dt}\right)}^2=\lambda G\frac{M}{r^2}{\cos }^2\alpha \sin \alpha \\ {\left(\frac{d\theta }{dt}\right)}^2=G\frac{M}{r^3}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right){\cos }^2\gamma \end{array}}$

El módulo de la velocidad de la nave espacial en coordenadas polares es

${\displaystyle \begin{array}{l}{v}^2={\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2={\tan }^2\gamma ·r^2{\left(\frac{d\theta }{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2=\frac{r^2}{{\cos }^2\gamma }{\left(\frac{d\theta }{dt}\right)}^2=\\ G\frac{M}{r}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)\end{array}}$

Ecuaciones paramétricas de la trayectoria

Obtenemos r en función del tiempo t

${\displaystyle \begin{array}{l}\frac{dr}{dt}=\tan \gamma ·r\frac{d\theta }{dt}=\tan \gamma ·r\sqrt{G\frac{M}{r^3}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right){\cos }^2\gamma }\\ {\displaystyle \underset{r_0}{\overset{r}{\int }}\sqrt{r}}dr=\sin \gamma \sqrt{GM\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)}·{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ r^{3/2}-r_0^{3/2}=\frac{3}{2}\sin \gamma \sqrt{GM\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)}·t\end{array}}$

Obtenemos θ en función del tiempo t

${\displaystyle \begin{array}{l}\frac{d\theta }{dt}=\frac{\cos \gamma }{r^{3/2}}\sqrt{GM\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\sin \alpha \right)\right)}\\ {\displaystyle \underset{0}{\overset{\theta }{\int }}d\theta =\cos \gamma \sqrt{GM\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\sin \alpha \right)\right)}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{dt}{r_0^{3/2}+\frac{3}{2}\sin \gamma \sqrt{GM\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)}·t}}}\end{array}}$

El resultado es

${\displaystyle \theta =\frac{2}{3\tan \gamma }\ln \left(1+\frac{3}{2}\sin \gamma \sqrt{\frac{GM}{r_0^3}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)}·t\right)}$

Tiempo de viaje desde r₀ a r₁

${\displaystyle T=\frac{2}{3}\frac{r_1^{3/2}-r_0^{3/2}}{\sin \gamma \sqrt{GM\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)}}}$

Las ecuaciones paramétricas (en función del tiempo t) de la trayectoria son

${\displaystyle \begin{array}{l}r=r_0{\left\{1+\left({\left(\frac{r_1}{r_0}\right)}^{3/2}-1\right)\frac{t}{T}\right\}}^{2/3}\hfill \\ \theta =\frac{2}{3\tan \gamma }\ln \left\{1+\left({\left(\frac{r_1}{r_0}\right)}^{3/2}-1\right)\frac{t}{T}\right\}\hfill \end{array}}$

Cuando llega a la posicíon final r=r₁

${\displaystyle {\theta }_1=\frac{1}{\tan \gamma }\ln \left(\frac{r}{r_0}\right)}$

Para una espiral hacia dentro r<r₀, el ángulo γ<0

Cálculo del ángulo γ

La segunda ecuación del movimiento, nos permite relacionar los ángulos γ y α

${\displaystyle r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}=\lambda G\frac{M}{r^2}{\cos }^2\alpha \sin \alpha }$

Teniendo en cuenta, la ecuación de la trayectoria. Partimos de

${\displaystyle \begin{array}{l}{\left(\frac{d\theta }{dt}\right)}^2=G\frac{M}{r^3}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right){\cos }^2\gamma \\ r_0^3\exp \left(3\theta ·\tan \gamma \right){\left(\frac{d\theta }{dt}\right)}^2=GM\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right){\cos }^2\gamma \end{array}}$

Derivamos con respecto del tiempo, el segundo miembro es constante

${\displaystyle \frac{d^2\theta }{d{t}^2}=-\frac{3}{2}\tan \gamma {\left(\frac{d\theta }{dt}\right)}^2}$

Introducimos ésta en la segunda ecuación del movimiento y teniendo en cuenta la expresión de dr/dt

${\displaystyle \begin{array}{l}\frac{1}{2}r\tan \gamma {\left(\frac{d\theta }{dt}\right)}^2=\lambda G\frac{M}{r^2}{\cos }^2\alpha \sin \alpha \\ \frac{1}{2}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)\sin \gamma \cos \gamma =\lambda {\cos }^2\alpha \sin \alpha \\ \left(1-\lambda {\cos }^3\alpha \right)\sin \gamma \cos \gamma -\lambda {\cos }^2\alpha \sin \alpha \left(1+{\cos }^2\gamma \right)=0\end{array}}$

Dado el ángulo α que forma la normal a la vela y la dirección radial, resolvemos la ecuación transcendente. Para que la espiral sea hacia dentro, el ángulo γ<0. Sea λ=0.3 y α=-10°

lambda=0.3;
alfa=-10*pi/180;
f=@(x) (1-lambda*cos(alfa)^3)*sin(x).*cos(x)-lambda*cos(alfa)^2*sin(alfa)*
(1+cos(x).^2);
fplot(f,[-pi/2,pi/2])
grid on
xlabel('\gamma')
ylabel('f(\gamma)')
title('Raices de la ecuación transcendente')

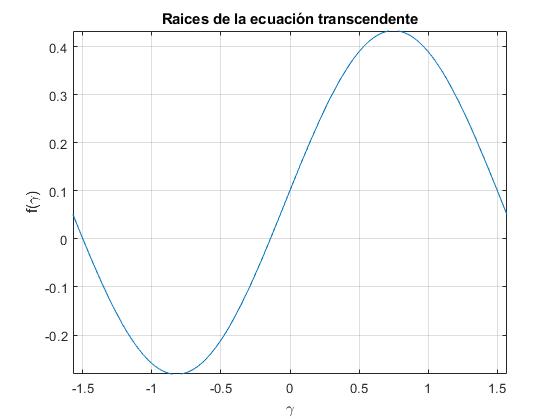
En la gráfica, vemos que hay dos posibles raíces, una cercana a 0 y otra a -π/2, tomamos la primera de ellas.

Calculamos γ mediante fzero de MATLAB y representamos la trayectoria espiral hacia dentro desde θ=0 hasta θ=8π

lambda=0.3;
alfa=-10*pi/180;
f=@(x) (1-lambda*cos(alfa)^3)*sin(x)*cos(x)-lambda*cos(alfa)^2*sin(alfa)*
(1+cos(x)^2);
gamma=fzero(f,[-pi/4,0]);
r0=1; %posición de partida, 1 UA
r=@(th) r0*exp(th*tan(gamma));
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x), [0,8*pi])
axis equal
grid on
xlabel('x (UA)')
ylabel('y (UA)')
title('Espiral logarítmica')

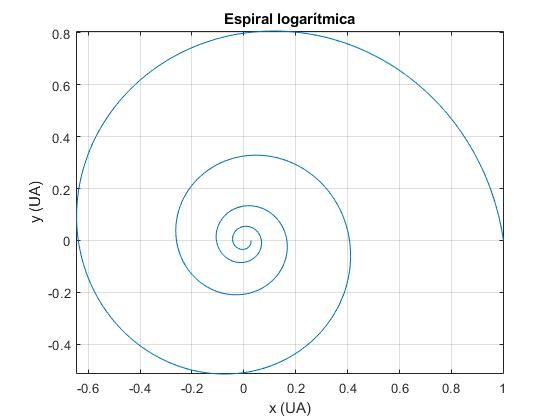
>> gamma*180/pi
-8.1425
>> r(8*pi) %posición de llegada
ans =    0.0274

>> M=1.98e30; %masa del Sol
>> G=6.67e-11; %constante
>> T=2*(r(8*pi)^(3/2)-r0^(3/2))*1.496e11^(3/2)/(3*sin(gamma)*
sqrt(G*M*(1+lambda*cos(alfa)^2*(sin(alfa)*tan(gamma)-cos(alfa)))));
>> T/(24*3600)
ans =  321.6399

El ángulo γ=-8.1425°. Cuando θ=8π, la distancia al Sol es r₁=0.0274 UA, empleando un tiempo T=321.6 días en viajar desde la posición r₀= 1 UA, θ=0

Trabajo-energía

El trabajo de las fuerzas que actúan sobre el cuerpo celeste es igual a la variación de energía cinética

La resultante de las fuerzas que actúan sobre la nave espacial de masa m es

${\displaystyle \frac{\overrightarrow{F}}{m}=\left(-G\frac{M}{r^2}+\lambda G\frac{M}{r^2}{\cos }^3\alpha \right)\widehat{r}+\left(\lambda G\frac{M}{r^2}{\cos }^2\alpha \sin \alpha \right)\widehat{\theta }=}$

El vector desplazamiento (en coordendas polares)

${\displaystyle \overrightarrow{dr}=dr·\widehat{r}+rd\theta ·\widehat{\theta }}$

Efectuamos el producto escalar e integramos para calcular el trabajo (por unidad de masa)

${\displaystyle \begin{array}{l}W={\displaystyle \underset{A}{\overset{B}{\int }}\frac{\overrightarrow{F}}{m}\overrightarrow{dr}}={\displaystyle \underset{A}{\overset{B}{\int }}\left\{\left(-G\frac{M}{r^2}+\lambda G\frac{M}{r^2}{\cos }^3\alpha \right)dr+\lambda G\frac{M}{r^2}{\cos }^2\alpha \sin \alpha ·r·d\theta \right\}}=\\ GM\left(1-\lambda {\cos }^3\alpha \right){\displaystyle \underset{r_0}{\overset{r}{\int }}-\frac{dr}{r^2}}+GM\lambda {\cos }^2\alpha \sin \alpha {\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\theta }{r_0\exp \left(\theta ·\tan \gamma \right)}}=\\ GM\left(1-\lambda {\cos }^3\alpha \right)\left(\frac{1}{r}-\frac{1}{r_0}\right)-GM\lambda {\cos }^2\alpha \sin \alpha \frac{1}{\tan \gamma }\left(\frac{1}{r}-\frac{1}{r_0}\right)=\\ GM\left(\frac{1}{r}-\frac{1}{r_0}\right)\left(1-\lambda {\cos }^3\alpha -\frac{\lambda {\cos }^2\alpha \sin \alpha }{\tan \gamma }\right)\end{array}}$

La variación de energía cinética es (véase la expresión de la velocidad v²)

${\displaystyle \begin{array}{l}\Delta E_k=\frac{1}{2}G\frac{M}{r}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)-\frac{1}{2}G\frac{M}{r_0}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)\\ =\frac{1}{2}GM\left(\frac{1}{r}-\frac{1}{r_0}\right)\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)\end{array}}$

Comprobamos que ambas expresiones son iguales por la relación existente entre los ángulos α y γ

${\displaystyle \left(1-\lambda {\cos }^3\alpha \right)\sin \gamma \cos \gamma -\lambda {\cos }^2\alpha \sin \alpha \left(1+{\cos }^2\gamma \right)=0}$

Efecto Oberth

El efecto Oberth ha sido estudiado en la página titulada El efecto Oberth. Una nave espacial inicialmente en órbita circular de radio r₀ alrededor del Sol, enciende sus motores durante un intervalo de tiempo muy pequeño para disminuir la velocidad. La nave espacial describe la mitad de una trayectoria elíptica. Cuando llega al perihelio enciende los motores para incrementar la velocidad y alcanzar el infinito con velocidad v_∞

En este apartado, la nave espacial inicialmente en órbita circular de radio r₀ alrededor del Sol con la vela desplegada perpendicular a la dirección radial α=0, gira la vela para formar un ángulo α (negativo) con el fin de describir una espiral logarítmica hacia dentro que le acerque al Sol. Cuando llegue a una distancia r₁, encenderá los motores durante un breve intervalo de tiempo, para incrementar la velocidad a la vez que gira la vela para que coincida la normal y la dirección radial, α=0

Esta maniobra sustituye la trayectoria elíptica por la espiral logarítmica, investigaremos si presenta alguna ventaja tanto en el consumo de combustible como en el tiempo de viaje durante la trayectoria intermedia

Orbita circular

La vela está orientada perpendicular a la dirección radial, α=0. La fuerza que actúa sobre la nave espacial con la vela desplegada es

${\displaystyle \overrightarrow{F}=-\frac{GMm}{r^2}(1-\lambda )\widehat{r}}$

Aplicamos la ecuación de la dinámica del movimiento circular uniforme.

${\displaystyle G\frac{Mm}{r_0^2}(1-\lambda )=m\frac{v_0^2}{r_0},v_0=\sqrt{\frac{GM}{r_0}(1-\lambda )}}$

Espiral logarítmica

En un momento dado se gira la vela, para que su normal forme un ángulo α (negativo) con el fin de describir una espiral logarítmica hacia dentro.

• Dado el ángulo α resolvemos la ecuación transcendente para calcular el ángulo γ

${\displaystyle \left(1-\lambda {\cos }^3\alpha \right)\sin \gamma \cos \gamma -\lambda {\cos }^2\alpha \sin \alpha \left(1+{\cos }^2\gamma \right)=0}$

• Calculamos la velocidad de la nave espacial V₀ en la posición inicial r₀

${\displaystyle V_0=\sqrt{\frac{GM}{r_0}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)}}$

La nave espacial enciende durante un intervalo muy pequeño de tiempo para cambiar su velocidad de v₀ a V₀

• Las ecuaciones paramétricas que describen la trayectoria son

${\displaystyle \begin{array}{l}r=r_0{\left\{1+\left({\left(\frac{r_f}{r_0}\right)}^{3/2}-1\right)\frac{t}{T}\right\}}^{2/3}\hfill \\ \theta =\frac{2}{3\tan \gamma }\ln \left\{1+\left({\left(\frac{r_f}{r_0}\right)}^{3/2}-1\right)\frac{t}{T}\right\}\hfill \end{array}}$

El ángulo final , para r=r₁ es

${\displaystyle {\theta }_1=\frac{1}{\tan \gamma }\ln \left(\frac{r_1}{r_0}\right)}$

• El tiempo T que emplea en describir esta trayectoria es

${\displaystyle T=\frac{2}{3}\frac{r_1^{3/2}-r_0^{3/2}}{\sin \gamma \sqrt{GM\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)}}}$

• La velocidad de la nave espacial v₁ en la posición final es

${\displaystyle v_1=\sqrt{\frac{GM}{r_1}\left(1+\lambda {\cos }^2\alpha \left(\sin \alpha \tan \gamma -\cos \alpha \right)\right)}}$

Impulso en el perihelio

La nave espacial enciende durante un intervalo muy pequeño de tiempo para cambiar su velocidad de v₁ a V₁=v₁+Δv a la vez que gira la vela en dirección perpendicular a la radial, α=0, con el fin de alcanzar la velocidad v_∞ en el infinito describiendo una trayectoria hiperbólica

El principio de conservación de la energía (por unidad de masa)

${\displaystyle \begin{array}{l}\frac{1}{2}{v}_{\infty }^2=\frac{1}{2}{\left(v_1+\Delta v\right)}^2-\frac{GM}{r_1}(1-\lambda )\\ \Delta v=\sqrt{v_{\infty }^2+2\frac{GM}{r_1}(1-\lambda )}-v_1\end{array}}$

Trayectoria final

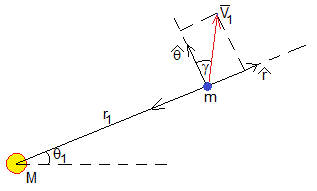
La nave espacial parte de la posición (r₁cosθ₁, r₁sinθ₁), con velocidad V₁=v₁+Δv, que forma un ángulo π/2-γ con la dirección radial

Para representar la trayectoria final, tenemos dos opciones: (véase la primera sección)

• Calcular los parámetros d y excentricidad ε y representar la hipérbola con el eje girado

• Resolver las ecuaciones diferenciales del movimiento

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-G\frac{M}{r^2}(1-\lambda )\frac{x}{r}\hfill \\ \frac{d^{2}y}{d{t}^2}=-G\frac{M}{r^2}(1-\lambda )\frac{y}{r}\hfill \end{array}}$

En el programa interactivo (más abajo) adoptamos la segunda solución

Ejemplo

La nave espacial provista de una vela de parámetro λ=0.3, describe una órbita circular de radio r₀=1.496·10¹¹ m (1 UA) alrededor del Sol cuya masa es M=1.98·10³⁰ kg. La constante G=6.67·10^-11 Nm²/kg²

La velocidad de la nave espacial con la vela desplegada perpendicular a la dirección radial α=0, es v₀=24.859 km/s, un poco menor que la velocidad de la misma nave espacial en órbita circular del mismo radio pero sin vela, 29.712 km/s

M=1.98e30; %masa del Sol
G=6.67e-11; %constante
r0=1.496e11; %posición de partida, 1 UA
lambda=0.3; %parámetro
v0=sqrt(G*M*(1-lambda)/r0);
...

Gira la vela para que la normal y la dirección radial formen un ángulo α=-10°, con el fin de que la nave espacial describa una espiral hacia dentro. Resolvemos la ecuación transcendente utilizando el procedimiento fzero de MATLAB para calcular el ángulo γ

...
alfa=-10*pi/180;
f=@(x) (1-lambda*cos(alfa)^3)*sin(x)*cos(x)-lambda*cos(alfa)^2*
sin(alfa)*(2-sin(x)^2);
gamma=fzero(f,[-pi/4,0]);
....

• Obtenemos γ=-0.1421 (-8.14°)

• Para pasar de la órbita circular a la espiral hemos de cambiar la velocidad de la nave de v₀=24.859 km/s a V₀=25.224 km/s

• La nave espacial va a viajar hacia el Sol hasta una distancia r₁=0.2 UA=2.9920·10¹⁰ m. El ángulo final es θ₁=11.2487 rad

• El tiempo que tarda en describir esta trayectoria T=2.5420·10⁷ s=294.2 días

• La velocidad de la nave espacial al final de esta trayectoria es v₁=56.6401 km/s

...
V0=sqrt(G*M*(1+lambda*cos(alfa)^2*(sin(alfa)*tan(gamma)-cos(alfa)))/r0);
r1=0.2*r0; %posición de llegada
th_1=log(r0/r1)/tan(gamma);
T=2*(r1^(3/2)-r0^(3/2))/(3*sin(gamma)*sqrt(G*M*(1+lambda*cos(alfa)^2*
(sin(alfa)*tan(gamma)-cos(alfa)))));
v1=sqrt(G*M*(1+lambda*cos(alfa)^2*(sin(alfa)*tan(gamma)-cos(alfa)))/r1);
...

Queremos que la nave espacial con la vela perpendicular a la dirección radial alcance el infinito con velocidad

${\displaystyle v_{\infty }=1.5\sqrt{\frac{GM}{r_0}}}$

La velocidad en la posición r₁ deberá ser V₁=v₁+Δv=90.365 km/s

A partir de este momento sigue una trayectoria hiperbólica que la lleva al infinito

El cambio de velocidad que experimenta la nave espacial al comienzo y al final de la trayectoria espiral es

Δv=(V₀-v₀)+(V₁-v₁)=(25.224-24.859)+(90.365-56.6401)=34.0899 km/s.

Casi todo el combustible se gasta en el segundo impulso.

M=1.98e30; %masa del Sol
G=6.67e-11; %constante
r0=1.496e11; %posición de partida, 1 UA
lambda=0.3;
v0=sqrt(G*M*(1-lambda)/r0);

alfa=-10*pi/180;
f=@(x) (1-lambda*cos(alfa)^3)*sin(x)*cos(x)-lambda*cos(alfa)^2*sin(alfa)*
(2-sin(x)^2);
gamma=fzero(f,[-pi/4,0]);
V0=sqrt(G*M*(1+lambda*cos(alfa)^2*(sin(alfa)*tan(gamma)-cos(alfa)))/r0);

r1=0.2*r0; %posición de llegada
th_1=log(r1/r0)/tan(gamma);
T=2*(r1^(3/2)-r0^(3/2))/(3*sin(gamma)*sqrt(G*M*(1+lambda*cos(alfa)^2*
(sin(alfa)*tan(gamma)-cos(alfa)))));
v1=sqrt(G*M*(1+lambda*cos(alfa)^2*(sin(alfa)*tan(gamma)-cos(alfa)))/r1);

v_inf=1.5*sqrt(G*M/r0);
V1=sqrt(v_inf^2+2*G*M*(1-lambda)/r1);
r=@(th) r0*exp(th*tan(gamma));
hold on
fplot(@(x) r0*cos(x), @(x) r0*sin(x), [0,2*pi], 'lineStyle','--')
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x), [0,th_1], 'color','r')

fg=@(t,x)[x(2);-G*M*(1-lambda)*x(1)/(sqrt(x(1)^2+x(3)^2))^3; x(4);
-G*M*(1-lambda)*x(3)/(sqrt(x(1)^2+x(3)^2))^3];
vx=V1*(sin(gamma)*cos(th_1)-cos(gamma)*sin(th_1));
vy=V1*(sin(gamma)*sin(th_1)+cos(gamma)*cos(th_1));
[~,x]=ode45(fg,[0,3e6],[r1*cos(th_1),vx,r1*sin(th_1),vy]);
plot(x(:,1),x(:,3),'b') %órbita elíptica
plot(0,0,'o','markersize',10,'markeredgecolor','r','markerfacecolor','y')
hold off
grid on
axis equal
xlabel('x (m)')
ylabel('y (m)')
title('Efecto Oberth')

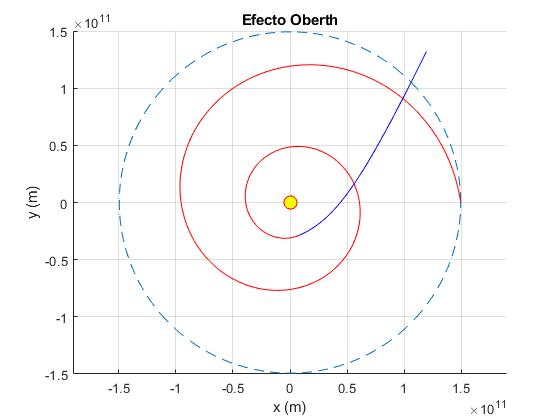
Comparación con la trayectoria elíptica intermedia

Vamos a comprobar si el cambio de la trayectoria intermedia de elíptica a espiral en el efecto Oberth presenta alguna ventaja

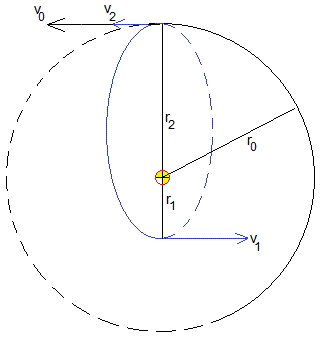
La nave espacial describe una órbita circular de radio r₀ con velocidad v₀

${\displaystyle v_0=\sqrt{\frac{GM}{r_0}}}$

La nave espacial disminuye su velocidad de v₀ a v₂ en el afelio de la trayectoria elíptica

${\displaystyle v_2=\sqrt{\frac{2GM{r}_1}{r_2(r_1+r_2)}}}$

En el perihelio, la nave espacial lleva un velocidad v₁=85.771 km/s,

${\displaystyle v_1=\sqrt{\frac{2GM{r}_2}{r_1(r_1+r_2)}}}$

mucho mayor que la que lleva la nave espacial en la trayectoria en espiral v₁=56.6401 km/s. El efecto Oberth debería ser más acusado con la trayectoria elíptica que con la trayectoria en espiral.

Se le proporciona una velocidad adicional para que alcance el infinito con velocidad v_∞. El cambio de velocidad en el perihelio es

${\displaystyle \frac{1}{2}{v}_{\infty }^2=\frac{1}{2}{v}_p^2-\frac{GM}{r_1},v_p=\sqrt{v_{\infty }^2+\frac{2GM}{r_1}}}$

Sabiendo que r₀=1.496·10¹¹ m (1 UA), r₁=0.2 UA y v_∞=1.5·v₀. Obtenemos, v₀=29.712 km/s, Δv_a=v₂-v₀=-12.558 km/s, Δv_p=v_p-v₁=18.221 km/s. Total, |Δv_a|+Δv_p=30.779 km/s

Se consume menos combustible en la trayectoria elíptica que en la espiral. El tiempo de viaje en la trayectoria elíptica es medio periodo, P_1/2=7.3515·10⁶ s (85 días) mucho menos que para la trayectoria espiral

${\displaystyle P_{1/2}=\frac{\pi }{\sqrt{GM}}{\left(\frac{r_0+r_1}{2}\right)}^{3/2}}$

M=1.98e30; %masa del Sol
G=6.67e-11; %constante
r0=1.496e11; %posición de partida, 1 UA
v0=sqrt(G*M/r0); %inicial en órbita circular
r2=r0; %afelio
r1=0.2*r0; %perihelio
%elípticar1=0.2*r2; %perihelio
v2=sqrt(2*G*M*r1/(r2*(r1+r2))); %afelio
v1=sqrt(2*G*M*r2/(r1*(r1+r2))); %perihelio
P_2=pi*((r1+r2)/2)^(3/2)/sqrt(G*M);
v_inf=1.5*v0; %velocidad en el infinito
vp=sqrt(v_inf^2+2*G*M/r1); %inicial hiperbólica
DVa=v2-v0; %cambios de velocidad
DVp=vp-v1;
disp([DVa,DVp])

Escalas

El script anterior es correcto, pero se puede hacer más eficiente, si se adoptan escalas de modo que las operaciones se efectúan entre números mucho más pequeños. Adoptamos las siguientes unidades (véase el primer apartado): la longitud se mide en UA (1.496·10¹¹ m), la unidad de tiempo P es el que tarda en dar una vuelta completa una nave espacial en órbita circular una UA de radio alrededor de Sol

${\displaystyle P=\frac{2\pi r_0}{v_0}=2\pi \sqrt{\frac{r_0^3}{GM}}}$

La velocidad se divide por

${\displaystyle \frac{1}{2\pi }\sqrt{\frac{GM}{r_0}}}$

r0=1; %posición de partida, 1 UA
lambda=0.3;
v0=2*pi*sqrt(1-lambda);

alfa=-10*pi/180;
f=@(x) (1-lambda*cos(alfa)^3)*sin(x)*cos(x)-lambda*cos(alfa)^2*sin(alfa)
*(2-sin(x)^2);
gamma=fzero(f,[-pi/4,0]);
V0=2*pi*sqrt((1+lambda*cos(alfa)^2*(sin(alfa)*tan(gamma)-cos(alfa))));

r1=0.2; %posición de llegada
th_1=log(r1/r0)/tan(gamma);
T=2*((r1/r0)^(3/2)-1)/(6*pi*sin(gamma)*sqrt(1+lambda*cos(alfa)^2*(sin(alfa)*
tan(gamma)-cos(alfa))));
v1=2*pi*sqrt((1+lambda*cos(alfa)^2*(sin(alfa)*tan(gamma)-cos(alfa)))*r0/r1);

v_inf=1.5;
V1=2*pi*sqrt(v_inf^2+2*(1-lambda)*r0/r1);
r=@(th) r0*exp(th*tan(gamma));
hold on
fplot(@(x) cos(x), @(x)sin(x), [0,2*pi], 'lineStyle','--')
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x), [0,th_1], 'color','r')

fg=@(t,x)[x(2);-4*pi^2*(1-lambda)*x(1)/(sqrt(x(1)^2+x(3)^2))^3; x(4);
-4*pi^2*(1-lambda)*x(3)/(sqrt(x(1)^2+x(3)^2))^3];
vx=V1*(sin(gamma)*cos(th_1)-cos(gamma)*sin(th_1));
vy=V1*(sin(gamma)*sin(th_1)+cos(gamma)*cos(th_1));
[~,x]=ode45(fg,[0,0.0948],[r1*cos(th_1),vx,r1*sin(th_1),vy]);
plot(x(:,1),x(:,3),'b') %órbita elíptica
plot(0,0,'o','markersize',10,'markeredgecolor','r','markerfacecolor','y')
hold off
grid on
axis equal
xlabel('x (UA)')
ylabel('y (UA)')
title('Efecto Oberth')

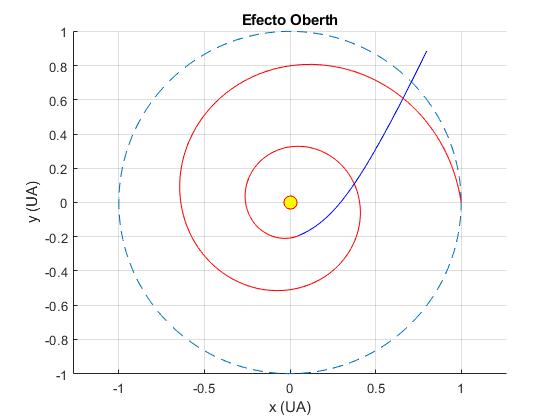
Actividades

Se introduce

• El parámetro λ, en el control titulado Parámetro
• El ángulo α (negativo) que forma la normal al plano de la vela con la dirección radial, en el control titulado Angulo vela
• La velocidad de la nave espacial muy lejos del Sol v_∞, en el control titulado Velocidad en el infinito
• La distancia más cercana (perihelio) al Sol r₁, en el control titulado Perihelio
• Se ha fijado el radio de la órbita circular inicial r₀=1 UA

Se pulsa el botón titulado Nuevo

Observamos la nave espacial (punto de color rojo) con la vela desplegada (un segmento de color blanco) en órbita circular alrededor del Sol.

Cuando describe media órbita enciende los motores durante un pequeño intervalo de tiempo a la ver que gira la vela un ángulo α (negativo) para incorporarla a una trayectoria espiral logarítmica que la acerque al Sol

Al final de la trayectoria espiral, la nave enciende de nuevo los motores para proporcionarle un impulso que le lleve al infinito con velocidad v_∞

Se representa las trayectorias y se proporcionan los datos de la distancia r de la nave al Sol y su velocidad v

En la parte izquierda, se representa el cambio de velocidad que experimenta la nave en los dos impulsos: en el afelio (órbita circular) y en el perihelio. Observamos que casi todo el combustible se gasta en el segundo impulso. En la parte derecha se proporcionan los datos de

• El tiempo parcial t desde el comienzo de cada una de las trayectorias
• La distancia r al centro del Sol en UA
• El módulo de la la velocidad, v

Referencias

Coryn A. L. Bailer-Jones. The sun diver: Combining solar sails with the Oberth effect. Am. J. Phys.89 (3), March 2021. pp. 235-243