Coordenadas polares

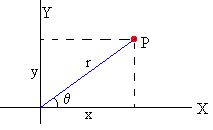
La posición de una partícula es (x, y) en coordenadas rectangulares y (r, θ) en coordenadas polares. La relación es

x=r·cosθ, y=r·sinθ

Expresamos la velocidad de la partícula en coordenadas polares

${\displaystyle \overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\widehat{r}\frac{dr}{dt}+r\frac{d\widehat{r}}{dt}}$

Calculamos las componentes rectangulares de los vectores unitarios $\widehat{r}$ y $\widehat{\theta }$

${\displaystyle \begin{array}{l}\widehat{r}=\widehat{i}\cos \theta +\widehat{j}\sin \theta \hfill \\ \widehat{\theta }=-\widehat{i}\sin \theta +\widehat{j}\cos \theta \hfill \end{array}}$

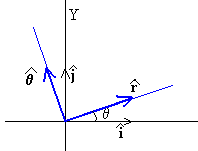
vemos que

${\displaystyle \begin{array}{l}\frac{d\widehat{r}}{dt}=(-\widehat{i}\sin \theta +\widehat{j}\cos \theta )\frac{d\theta }{dt}=\widehat{\theta }\frac{d\theta }{dt}\hfill \\ \frac{d\widehat{\theta }}{dt}=(-\widehat{i}\cos \theta -\widehat{j}\sin \theta )\frac{d\theta }{dt}=-\widehat{r}\frac{d\theta }{dt}\hfill \end{array}}$

Las expresión del vector velocidad en coordenadas polares es

${\displaystyle \overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }}$

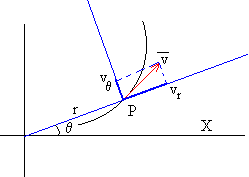
Las expresión del vector aceleración es:

${\displaystyle \begin{array}{l}\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\widehat{r}}{dt}+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }+r\frac{d\theta }{dt}\frac{d\widehat{\theta }}{dt}=\hfill \\ \frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }-r{\left(\frac{d\theta }{dt}\right)}^2\widehat{r}=\hfill \\ \left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\hfill \end{array}}$

Ecuaciones del movimiento de las partículas

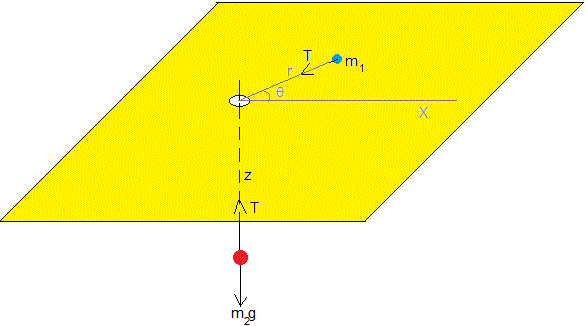
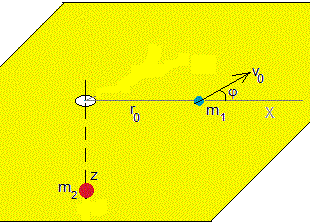
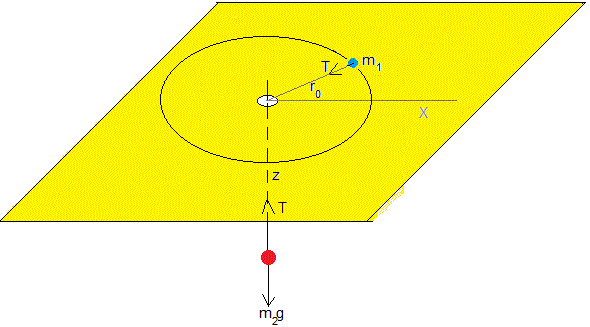
Supongamos dos cuerpos de masas m₁ y m₂ unidos por una cuerda inextensible y de masa despreciable que pasa a través de un pequeño agujero hecho en un tablero. El primer cuerpo se puede mover en el plano horizontal, mientras que el segundo se puede mover hacia arriba o hacia abajo a lo largo del eje vertical Z, tal como se muestra en la figura. Consideramos únicamente la situación ideal sin rozamiento alguno.

• Sobre el cuerpo de masa m₁ actúa la tensión T de la cuerda a lo largo de la dirección radial.
• Sobre el cuerpo de masa m₂ actúa la tensión de la cuerda y su peso m₂g

Establecemos un sistema de referencia, de modo que el origen está en el orificio hecho en la tabla, el eje Z apunta hacia abajo, la posición del cuerpo m₂ es z y la posición del cuerpo m₁ viene determinado por su distancia radial r al orificio y el ángulo θ que hace con el eje X, tal como se muestra en la figura. Si la longitud de la cuerda es l, se cumple que r+z=l.

La ecuación del movimiento de m₂ es

${\displaystyle m_2\frac{d^{2}z}{d{t}^2}=m_{2}g-T}$

o bien,

${\displaystyle -m_2\frac{d^{2}r}{d{t}^2}=m_{2}g-T}$

En el primer apartado, hemos obtenido las expresiones de las componentes del vector aceleración en coordenadas polares. Formulamos la segunda ley de Newton para cada una de las componentes, teniendo en cuenta que la única fuerza que actúa sobre la partícula (la tensión de la cuerda) tiene dirección radial y sentido hacia el origen.

${\displaystyle \begin{array}{l}{m}_1\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=-T\\ m_1\left(r\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dr}{dt}\right)=0\end{array}}$

La segunda ecuación nos indica que el momento angular L (expresado en coordenadas polares es constante)

${\displaystyle \frac{d}{dt}\left(r^2\frac{d\theta }{dt}\right)=0r^2\frac{d\theta }{dt}=\frac{L}{m_1}=\text{cte}}$

Teniendo en cuenta la constancia del momento angular L y eliminado la tensión T de la cuerda en las ecuaciones del movimiento de las dos partículas, llegamos a la ecuación diferencial que describe el movimiento de la partícula de masa m₁ en la dirección radial, r.

${\displaystyle \begin{array}{l}{m}_1\left(\frac{d^{2}r}{d{t}^2}-\frac{L^2}{m_1^2{r}^3}\right)=-m_{2}g-m_2\frac{d^{2}r}{d{t}^2}\\ (m_1+m_2)\frac{d^{2}r}{d{t}^2}-\frac{L^2}{m_1{r}^3}=-m_{2}g\end{array}}$

Las ecuaciones diferenciales que describen el movimiento de la partícula sobre el tablero en coordenadas polares (r, θ), son por tanto,

${\displaystyle \begin{array}{l}\frac{d^{2}r}{d{t}^2}-\frac{L^2}{m_1(m_1+m_2)r^3}=-\frac{m_2}{(m_1+m_2)}g\\ \frac{d\theta }{dt}=\frac{L}{m_1{r}^2}\end{array}}$

Con las condiciones iniciales siguientes: la partícula parte en el instante t=0 de la posición r₀, θ=0, con velocidad dr/dt=v₀cosφ, r₀(dθ/dt)₀=v₀sinφ.

El momento angular L=m₁r₀v₀sinφ

Energía del sistema de partículas

Establecemos el nivel cero de energía potencial en origen z=0. La energía E del sistema de dos partículas es constante

${\displaystyle E=\frac{1}{2}{m}_1{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}{m}_1{r}^2{\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}{m}_2{\left(\frac{dz}{dt}\right)}^2-m_{2}gz}$

Teniendo en cuenta la constancia del momento angular L y que z+r=l

${\displaystyle E=\frac{1}{2}(m_1+m_2){\left(\frac{dr}{dt}\right)}^2+\frac{L^2}{2m_1{r}^2}-m_{2}g\left(l-r\right)}$

La energía inicial del sistema en el instante t=0 es

${\displaystyle E=\frac{1}{2}{m}_1{v}_0^2+\frac{1}{2}{m}_2{v}_0^2{\cos }^2\phi -m_{2}g(l-r_0)}$

Derivando esta ecuación con respecto del tiempo y teniendo en cuenta, que la energía E es constante, dE/dt=0, obtenemos la ecuación del movimiento de m₁ en la dirección radial.

En los puntos de máximo acercamiento o alejamiento, al origen, dr/dt=0, la velocidad en la dirección radial se hace cero, obtenemos una ecuación cúbica a partir de la cual obtenemos r_min y r_max, véase el ejemplo más abajo

Casos particulares

Dos situaciones se analizan a nivel elemental

Movimiento en la dirección radial

La situación más sencilla, es aquella en la que m₁ en reposo, se libera y se mueve en dirección radial. Las ecuaciones del movimiento en la dirección radial para la partícula de masa m₁ y de la partícula de masa m₂ a lo largo del eje Z, son

${\displaystyle \begin{array}{l}{m}_1\frac{d^{2}r}{d{t}^2}=-T\\ m_2\frac{d^{2}z}{d{t}^2}=m_{2}g-T\end{array}}$

Teniendo en cuenta que z+r=l y eliminando la tensión T, vemos que la aceleración de las partículas es constante, m₂g/(m₁+m₂), para m₂ y de signo contrario para m₁. La distancia radial r de la partícula m₁ en función del tiempo t es

${\displaystyle r=r_0-\frac{1}{2}\frac{m_2}{m_1+m_2}g{t}^2}$

Movimiento circular uniforme

Para que la partícula de masa m₁ describa una trayectoria circular de radio r₀, bajo la acción de la tensión T=m₂g, tiene que llevar una velocidad angular ω₀, tal que se cumpla la ecuación de la dinámica del movimiento circular uniforme (fuerza =masa por aceleración normal)

${\displaystyle m_{2}g=m_1{\omega }_0^2{r}_0{\omega }_0=\sqrt{\frac{m_2}{m_1}\frac{g}{r_0}}}$

Por ejemplo, para r₀=3, m₁=1, m₂=0.365. La partícula describe un movimiento circular uniforme si se mueve con velocidad angular constante ω₀=1.1030. El periodo o tiempo que tarda en dar una vuelta completa es 2π/ω₀=5.6963

Trayectorias casi circulares

Para una trayectoria circular el momento angular L es

${\displaystyle L=m_1{r}_0^2{\omega }_0=\sqrt{m_1{m}_{2}g{r}_0^3}}$

Escribiendo r=r₀+x con x<<r₀, la ecuación del movimiento en la dirección radial es

${\displaystyle \frac{d^{2}x}{d{t}^2}-\frac{m_{2}g{r}_0^3}{(m_1+m_2){\left(r_0+x\right)}^3}=-\frac{m_2}{(m_1+m_2)}g}$

Utilizando la aproximación,

${\displaystyle \frac{1}{{\left(r_0+x\right)}^3}\approx \frac{1}{r_0^3}\left(1-\frac{3x}{r_0}\right)}$

Nos queda la ecuación

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{3m_{2}g}{(m_1+m_2)r_0}x=0}$

Que representa un Movimiento Armónico Simple de periodo

${\displaystyle P=2\pi \sqrt{\frac{(m_1+m_2)r_0}{3m_{2}g}}}$

Trayectorias

Resolvemos, el sistema de dos ecuaciones diferenciales por procedimientos numéricos, para obtener la posición de la partícula (r,θ) en cada instante t con las siguientes condiciones iniciales, en el instante t=0, r=r₀, dr/dt=0 y dθ/dt=ω₀

El momento angular y la energía valen

${\displaystyle \begin{array}{l}L=m_1{r}_0^2{\omega }_0\\ E=\frac{1}{2}{m}_1{\left(r_0{\omega }_0\right)}^2-m_{2}g(l-r_0)\end{array}}$

El principio de conservación de la energía se escribe

${\displaystyle \frac{1}{2}{m}_1{\left(r_0{\omega }_0\right)}^2+m_{2}g{r}_0=\frac{1}{2}(m_1+m_2){\left(\frac{dr}{dt}\right)}^2+\frac{m_1{r}_0^4{\omega }_0^2}{2r^2}+m_{2}gr}$

Poniendo dr/dt=0, calculamos la máxima y mínima distancia de alejamiento de la partícula de masa m₁ al origen, las raíces positivas de la ecuación cúbica

${\displaystyle 2m_{2}g{r}^3-\left(m_1{\left(r_0{\omega }_0\right)}^2+2m_{2}g{r}_0\right)r^2+m_1{r}_0^4{\omega }_0^2=0}$

Para calcular las raíces de una ecuación cúbica utilizamos el procedimiento descrito en la página titulada Raíces de una ecuación (I)

m1=1; %masa de la partícula sobre el plano horizontal
m2=0.365; %masa de la partícula que cuelga
w0=0.6;  %velocidad angular inicial en la 
r0=3;		%posición inicial r0, que se mantiene fija
tf=10;	%tiempo final, ajustar

L=m1*r0^2*w0;  %momento angular constante
x0=[r0,0,0];	%condiciones iniciales
%x(1) es r, x(2) es dr/dt, x(3) es theta
fg=@(t,x) [x(2); L^2/(m1*(m1+m2)*x(1)^3)-m2*9.8/(m1+m2);L/(m1*x(1)^2)];
[t,x]=ode45(fg,[0,tf],x0);
plot(x(:,1).*cos(x(:,3)), x(:,1).*sin(x(:,3)))
grid on
xlabel('r')
ylabel('\theta')
axis equal
figure
%raíces de la ecuación cúbica, máximo y mínimo acercamiento
subplot(2,1,1)
a=2*m2*9.8;
b=-(m1*r0^2*w0^2+2*m2*9.8*r0);
d=m1*r0^4*w0^2;
p=[1,b/a,0,d/a];
dist=raices_3(p);
hold on
for i=1:3
    if dist(i)>0
        line([0,10],[dist(i),dist(i)],'lineStyle','--','color','k')
    end
end
plot(t,x(:,1))
hold off
grid on
xlabel('t')
ylabel('r')
subplot(2,1,2)
plot(t,x(:,3))
grid on
xlabel('t')
ylabel('\theta')

Se representa la trayectoria de la partícula sobre el plano horizontal

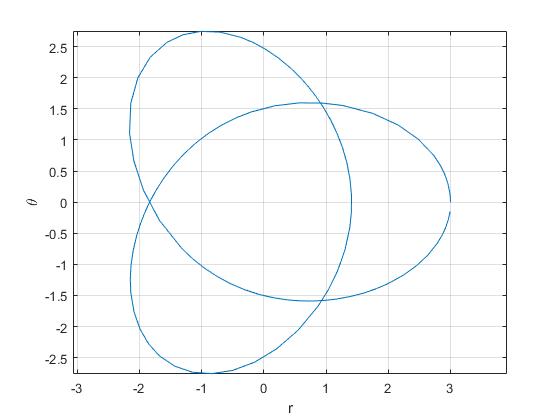
Se representa sus coordenadas (r, θ) en función del tiempo t

Las líneas a trazos señalan, las distancias de máximo y mínimo acercamiento de la partícula de masa m₁ al origen, las raíces positivas de la ecuación cúbica

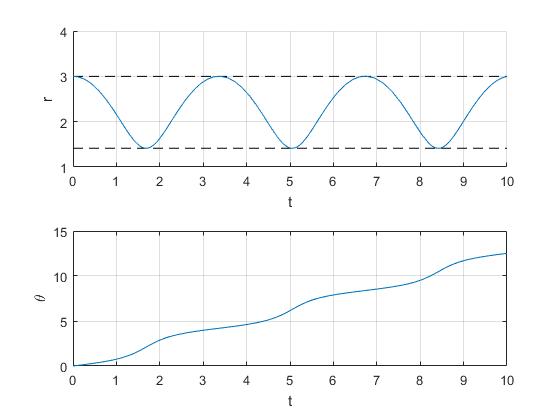
Comprobamos que la energía es aproximadamente constante en todos los puntos de la trayectoria

>> 0.5*(m1+m2)*x(:,2).^2+L^2./(2*m1*x(:,1).^2)+m2*9.8*x(:,1)
ans =
   12.3510
   12.3510
   12.3510
   ......

Trayectorias casi circulares

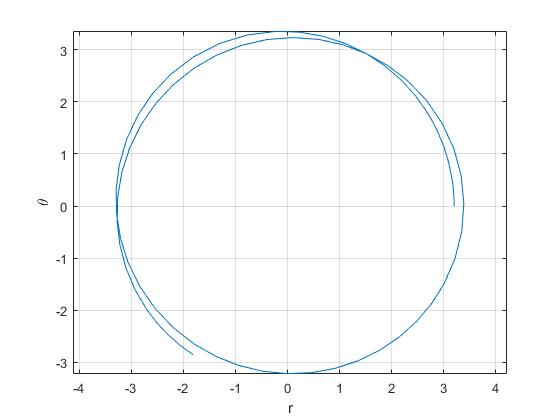
Para que se produzca una trayectoria circular de radio r₀=3, la velocidad angular ω₀=1.1030 rad/s. Cambiamos las condiciones iniciales de modo que r₀=3.2, vemos que se produce una oscilación en la dirección radial de periodo P=4.0 s

m1=1; %masa de la partícula sobre el plano horizontal
m2=0.365; %masa de la partícula que cuelga
w0=1.1030;  %velocidad angular inicial en la 
r0=3.2;		%posición inicial r0, que se mantiene fija
tf=10;	%tiempo final, ajustar
....

Se representa la trayectoria de la partícula sobre el plano horizontal

Se representa sus coordenadas (r, θ) en función del tiempo t

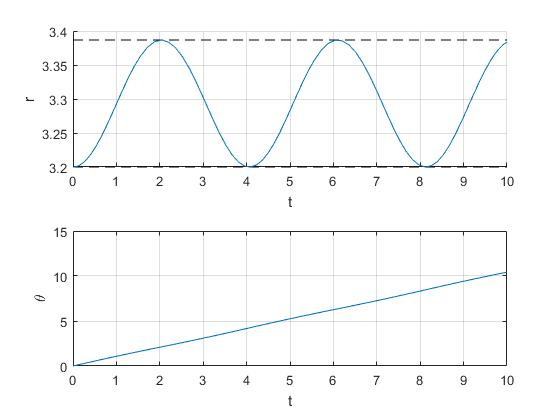
Como vemos en la gráfica, el tiempo entre dos máximos de la distancia radial r es aproximadamente 4 s. Calculamos el periodo de las oscilación radial

>> P=2*pi*sqrt((m1+m2)*r0/(3*m2*9.8))
P =   4.0087

Como la velocidad angular es casi constante e igual a ω₀, la posición angular θ≈ω₀t (gráfica inferior)

Estos ejemplos reproducen algunas de las figuras del artículo citado en las referencias

Actividades

Se introduce

• La masa m₁, de la partícula que se mueve en el plano horizontal, en el control titulado Masa m₁
• La masa m₂, de la partícula que cuelga, en el control titulado Masa m₂
• La velocidad angular inicial dθ/dt=ω₀, de la primera partícula, en el control titulado Velocidad angular ω₀
• La partícula se situa sobre el eje X, θ=0, a una distancia r₀=3 del origen, posición en coordenadas polares (3,0). Su velocidad radial inicial dr/dt=0

Se pulsa el botón titulado Nuevo, se dibuja la trayectoria de la partícula sobre el plano horizontal.

En la parte inferior izquierda, se muestra en color rojo el tanto por ciento de error, la cantidad

${\displaystyle \frac{\left|E-E_0\right|}{E_0}100}$

Donde E₀ es la energía inicial y E es la energía en el instante t.

Cuando este cociente es mayor que la unidad, 1% se considera que el programa interactivo no resuelve correctamente el sistema de ecuaciones diferenciales y se detiene.

Se pulsa el botón pausa ||, para parar el movimiento y el botón paso a paso >| para acercarnos al momento en el que el móvil completa una trayectoria y vuelve a repetir el movimiento. De este modo, medimos el periodo. En la parte superior izquierda, se muestra el tiempo y en los ejes, se marca las coordenadas del móvil.

Referencias

William Sacks, Alain Mauger. Two balls and a string: from ordered motion to chaos. Eur. J. Phys. 34 (2013) 1487-1506