Una solución analítica sencilla

Un astronauta que sale de la nave espacial adquiere su velocidad relativa mediante el impulso de pequeños cohetes situados en su mochila, o mediante la acción de los músculos de sus brazos o sus piernas apoyados en el exterior de la nave. En ambos casos, la velocidad relativa u del astronauta respecto de la nave espacial es muy pequeña comparada con la velocidad v₀ de la nave, y el tiempo que tarda en moverse de un lugar a otro es muy pequeño comparado con el periodo P₀ o tiempo que tarda la nave en completar una órbita.

En la siguiente tabla, se proporcionan algunos datos.

Sin embargo, como vamos a comprobar en este apartado, la desviación de la trayectoria seguida por el astronauta u otro cuerpo cualquiera respecto de la rectilínea es muy acusada incluso para pequeños desplazamientos.

De nuevo, consideramos que la nave espacial se mueve en una órbita circular de radio r₀.

En el Sistema de Referencia (S. R.) Inercial cuyo origen es el centro de la Tierra, la posición de la nave espacial viene dada por el vector $\overrightarrow{r_0}$ , de módulo r₀ constante y que gira con velocidad angular constante ω=v₀/r₀. La posición del cuerpo está indicada por el vector $\overrightarrow{r}$

Describimos el movimiento del astronauta en el S. R. no Inercial con origen en la nave y cuyos ejes son la dirección radial y tangencial, respectivamente. Estos ejes que denominaremos X’ e Y’ giran con velocidad angular ω, vistos desde el S. R. Inercial situado en la Tierra

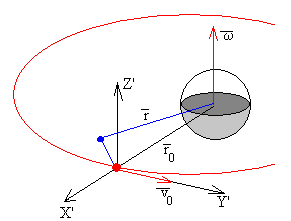
Las fórmulas que relacionan la velocidad $\overrightarrow{v}\text{'}$ y de la aceleración $\overrightarrow{a}\text{'}$ medidas en el S. R. no Inercial con la velocidad $\overrightarrow{v}$ y aceleración $\overrightarrow{a}$ medidas en el S. R. Inercial son las siguientes:

${\displaystyle \begin{array}{l}\overrightarrow{v}\text{'}=\overrightarrow{v}-\overrightarrow{\omega }\times \overrightarrow{r}\hfill \\ \overrightarrow{a}\text{'}=\overrightarrow{a}-2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r}\hfill \end{array}}$

$\overrightarrow{\omega }=\omega \widehat{k}$ es el vector velocidad angular de rotación cuya dirección (eje Z) es perpendicular al plano de la órbita y cuyo sentido apunta hacia el lector, si la nave espacial gira en sentido antihorario, $\overrightarrow{v}\text{'}$ es la velocidad del astronauta en el S. R. no Inercial. Restringiremos el movimiento del cuerpo al plano de la órbita de la nave.

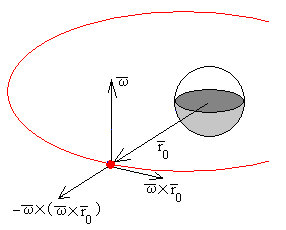
Para obtener una expresión analítica sencilla, supondremos que las fuerza de atracción gravitatoria y la fuerza centrífuga son iguales y opuestas en las proximidades de la órbita circular de radio r₀, en la que se va a mover el cuerpo. Esta es la razón de la sensación de carencia de peso que experimenta un astronauta en el interior de la nave y por la cual, observamos a éstos moverse libremente.

${\displaystyle \overrightarrow{a}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r}=-G\frac{M}{r^3}\overrightarrow{r}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r}=0}$

Supondremos por tanto, que la única aceleración que afecta al cuerpo en el S. R. ligado a la nave es la de Coriolis.

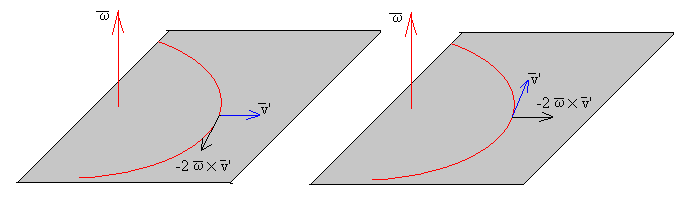
La aceleración $\overrightarrow{a}\text{'}$ del astronauta en el S. R. no Inercial es

${\displaystyle \overrightarrow{a}\text{'}\approx -2\omega \widehat{k}\times (v_{x\text{'}}\widehat{i}+v_{y\text{'}}\widehat{j})=2\omega v_{y\text{'}}\widehat{i}-2\omega v_{x\text{'}}\widehat{j}}$

En forma de ecuación diferencial, escribiremos

${\displaystyle \begin{array}{l}\frac{d^{2}x\text{'}}{d{t}^2}=2\omega \frac{dy\text{'}}{dt}\\ \frac{d^{2}y\text{'}}{d{t}^2}=-2\omega \frac{dx\text{'}}{dt}\end{array}}$

Derivando de nuevo con respecto del tiempo, se desacoplan las dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^{3}x\text{'}}{d{t}^3}=-4{\omega }^2\frac{dx\text{'}}{dt}\frac{d^2{v}_{x\text{'}}}{d{t}^2}+4{\omega }^2{v}_{x\text{'}}=\text{0 }\\ \frac{d^{3}y\text{'}}{d{t}^3}=-4{\omega }^2\frac{dy\text{'}}{dt}\frac{d^2{v}_{y\text{'}}}{d{t}^2}+4{\omega }^2{v}_{y\text{'}}=\text{0}\end{array}}$

Tenemos dos ecuaciones diferenciales cuya solución es similar a la de un Movimiento Armónico Simple (MAS) pero en la velocidad (no en la posición).

v_x’=Asin(2ωt)+Bcos(2ωt)
v_y’=Csin(2ωt)+Dcos(2ωt)

Los coeficientes A, B, C y D se determinan a partir de las condiciones iniciales: en el instante t=0, el cuerpo sale del origen x’=0, y’=0 con velocidad inicial v_0x’=u·cosα, v_0y’=u·sinα, y cuyas componentes de la aceleración (derivada de la velocidad) inicial son a_0x’=2ωv_0y’ y a_0y’= -2ωv_0x’

${\displaystyle \begin{array}{l}\frac{dx\text{'}}{dt}=v_{0y\text{'}}\text{sin}(2\omega t)+v_{0x\text{'}}\cos (2\omega t)\\ \frac{dy\text{'}}{dt}=-v_{0x\text{'}}\text{sin}(2\omega t)+v_{0y\text{'}}\cos (2\omega t)\end{array}}$

Integramos de nuevo, teniendo en cuenta que el cuerpo sale del origen x’=0, y’=0 en el instante t=0.

${\displaystyle \begin{array}{l}x\text{'}=\frac{1}{2\omega }\left(-v_{0y\text{'}}\text{cos}(2\omega t)+v_{0x\text{'}}\text{sin}(2\omega t)+v_{0y\text{'}}\right)\\ y\text{'}=\frac{1}{2\omega }\left(v_{0x\text{'}}\text{cos}(2\omega t)+v_{0y\text{'}}\text{sin}(2\omega t)-v_{0x\text{'}}\right)\end{array}}$

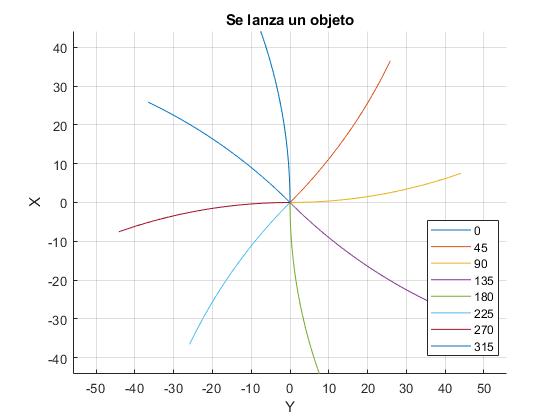
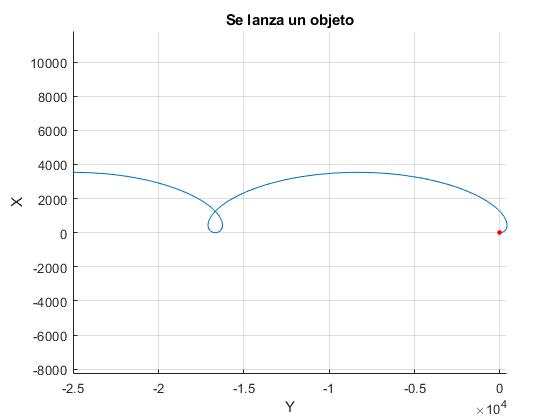
En la figura, se muestra las trayectorias seguidas por un cuerpo lanzado desde la nave espacial con una velocidad de u=0.3 m/s en varias direcciones. La nave espacial se encuentra describiendo una órbita circular de 400 km de altura. Cuanto menor es la velocidad del cuerpo, y cuanto mayor es la velocidad angular de la nave espacial más se desvía la trayectoria seguida por el cuerpo de la rectilínea.

w=0.00113; %velocidad angular de rotación
u=0.3; %velocidad inicial
hold on
for ang=0:pi/4:2*pi-pi/4 %ángulos (0 es la dirección radial)
    v0x=u*cos(ang);
    v0y=u*sin(ang);
    x=@(t) (-v0y*cos(2*w*t)+v0x*sin(2*w*t)+v0y)/(2*w);
    y=@(t) (v0x*cos(2*w*t)+v0y*sin(2*w*t)-v0x)/(2*w);
    fplot(y,x,[0,150],'displayName',num2str(ang*180/pi))
end
hold off
axis equal
grid on
axis equal
legend('-DynamicLegend','location','best')
xlabel('Y')
ylabel('X')
title('Se lanza un objeto')

Casos particulares

1. El cuerpo se lanza en la dirección radial (a lo largo del eje X’) v_0y’=0, ángulo α=0



${\displaystyle \begin{array}{l}x\text{'}=\frac{v_{0x\text{'}}}{2\omega }\text{sin}(2\omega t)\\ y\text{'}=\frac{v_{0x\text{'}}}{2\omega }\cos (2\omega t)-\frac{v_{0x}}{2\omega }\end{array}}$

La trayectoria es una circunferencia cuyo centro está en (0, -a)

${\displaystyle x{\text{'}}^2+{(y\text{'}+a)}^2=a^{2}a=\frac{v_{0x\text{'}}}{2\omega }}$

2. El cuerpo se lanza en la dirección tangencial (eje Y’), v_0x’=0, ángulo α=90°



${\displaystyle \begin{array}{l}x\text{'}=-\frac{v_{0y\text{'}}}{2\omega }\text{cos}(2\omega t)+\frac{v_{0y\text{'}}}{2\omega }\\ y\text{'}=\frac{v_{0y\text{'}}}{2\omega }\text{sin}(2\omega t)\end{array}}$

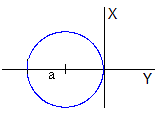
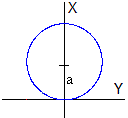
La trayectoria es una circunferencia cuyo centro está en (a, 0)

${\displaystyle {(x\text{'}-a)}^2+y{\text{'}}^2=a^{2}a=\frac{v_{0y\text{'}}}{2\omega }}$

Actividades

Se introduce

• La altura en km de la nave espacial respecto de la superficie de la Tierra, en el control titulado Altura

• La velocidad u del cuerpo que es lanzado desde la nave espacial, en el control titulado Velocidad

• La dirección α de dicha velocidad, en el control titulado Ángulo

• El ángulo α=0, corresponde a un lanzamiento hacia arriba (en la dirección radial o eje X’),

• α=90º, el lanzamiento es hacia delante, en la misma dirección (tangencial o eje Y’)  y sentido que la velocidad de la nave.

• α=180º, corresponde a un lanzamiento hacia abajo, en dirección hacia el centro de la Tierra

• α=270º, el lanzamiento hacia atrás, en la misma dirección (tangencial)  y en  sentido contrario a la velocidad de la nave.

Se pulsa el botón titulado Nuevo

Se representa una estación espacial de 100 m de longitud. Se lanza un cuerpo desde el centro de la nave en una determinada dirección.

La recta de color rojo, señala la trayectoria que seguiría el cuerpo en una nave espacial situada en una región libre de fuerzas. La curva en color azul señala la trayectoria del cuerpo cuya dirección de la velocidad es desviada por la aceleración de Coriolis.

Podemos medir la desviación que experimenta el astronauta y la influencia de la altura de la nave espacial o de su distancia al centro de la Tierra, r₀, la dirección α de la velocidad inicial y el módulo u de dicha velocidad.

Para obtener las trayectorias circulares de los caos particulares, se introduce en el control titulado Velocidad, u=0.03 m/s, y en el control titulado Angulo, α=0 y después, α=90°

Una solución analítica más completa

La solución dada en el apartado anterior es válida solamente:

• Cuando el cuerpo se mueve en las proximidades de la nave espacial

• Cuando el tiempo de viaje es una pequeña fracción del periodo orbital

En este apartado, presentamos una solución que no realiza unas aproximaciones tan drásticas y por tanto, hacen que su validez sea más general.

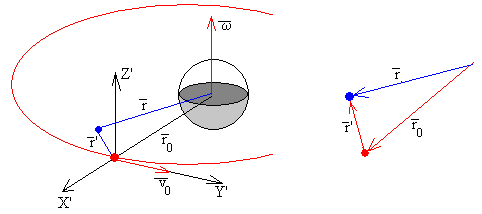
La fórmula que relaciona la aceleración $\overrightarrow{a}\text{'}$ medidas en el S. R. no inercial con la aceleración $\overrightarrow{a}$ medida en el S. R. inercial es la siguiente:

${\displaystyle \overrightarrow{a}\text{'}=\overrightarrow{a}-2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r}}$

• La aceleración $\overrightarrow{a}$ es la fuerza de atracción por unidad de masa (o intensidad del campo gravitatorio $\overrightarrow{g}$ ) que tiene dirección radial y sentido hacia el centro de la Tierra

${\displaystyle \overrightarrow{a}=-G\frac{M}{r^3}\overrightarrow{r}}$

• El término $-2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}$ es la aceleración de Coriolis

• El término $-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r}$ es la aceleración centrífuga

• $\overrightarrow{\omega }=\omega \widehat{k}$ es el vector velocidad angular de rotación cuya dirección (eje Z) es perpendicular al plano de la órbita y cuyo sentido apunta hacia el lector, si la nave espacial gira en sentido antihorario, ω=v₀/r₀.

• $\overrightarrow{v}\text{'}$ es la velocidad del cuerpo en el S. R. no Inercial

• $\overrightarrow{r_0}$ es el vector que señala la posición de la nave espacial en el S.R. inercial

• $\overrightarrow{r}$ es la posición del cuerpo en el S. R. Inercial

• $\overrightarrow{r}\text{'}$ es la posición del cuerpo en el S. R. no Inercial

La relación entre los tres vectores es $\overrightarrow{r}=\overrightarrow{r_0}+\overrightarrow{r\text{'}}$

La aceleración $\overrightarrow{a}\text{'}$ se escribe

${\displaystyle \overrightarrow{a}\text{'}=-\frac{GM}{r^3}\left(\overrightarrow{r_0}+\overrightarrow{r}\text{'}\right)-2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \left(\overrightarrow{r_0}+\overrightarrow{r}\text{'}\right)}$

Si la distancia entre el cuerpo y la nave espacial se mantiene pequeña comparada el radio r₀ de la órbita de la nave espacial, desarrollamos en serie, la aceleración de la gravedad y despreciamos los términos en (r’/r₀)².

El módulo del vector $\overrightarrow{r}=\overrightarrow{r_0}+\overrightarrow{r\text{'}}$, es

${\displaystyle r^2=r_0^2+r{\text{'}}^2+2\overrightarrow{r\text{'}}·\overrightarrow{r_0}}$

El módulo de la aceleración de la gravedad se aproxima a

${\displaystyle \begin{array}{l}\frac{GM}{r^3}=\frac{GM}{r_0^3}{\left(1+\frac{r{\text{'}}^2}{r_0^2}+2\frac{\overrightarrow{r\text{'}}·\overrightarrow{r_0}}{r_0^2}\right)}^{-3/2}\approx \frac{GM}{r_0^3}{\left(1+2\frac{\overrightarrow{r\text{'}}·\overrightarrow{r_0}}{r_0^2}\right)}^{-3/2}\\ \approx \frac{GM}{r_0^3}\left(1-3\frac{\overrightarrow{r\text{'}}·\overrightarrow{r_0}}{r_0^2}\right)\end{array}}$

La aceleración $\overrightarrow{a}\text{'}$ del cuerpo en el S. R. no Inercial es

${\displaystyle \begin{array}{l}\overrightarrow{a}\text{'}=-\frac{GM}{r^3}\left(\overrightarrow{r_0}+\overrightarrow{r\text{'}}\right)-2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \left(\overrightarrow{r_0}+\overrightarrow{r}\text{'}\right)\hfill \\ \begin{array}{l}\overrightarrow{a}\text{'}\approx -\frac{GM}{r_0^3}\overrightarrow{r_0}-\frac{GM}{r_0^3}\overrightarrow{r\text{'}}+\frac{GM}{r_0^3}3\frac{\overrightarrow{r\text{'}}·\overrightarrow{r_0}}{r_0^2}\overrightarrow{r_0}+\frac{GM}{r_0^3}3\frac{\overrightarrow{r\text{'}}·\overrightarrow{r_0}}{r_0^2}\overrightarrow{r\text{'}}\\ -2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r_0}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r}\text{'}\end{array}\hfill \end{array}}$

En una órbita circular de radio r₀, la fuerza centrífuga y la fuerza de atracción se anulan, de modo que se cancelan el primer y sexto término de la larga expresión de la aceleración $\overrightarrow{a}\text{'}$ y además, se desprecia el cuarto término proporcional a r'²/r₀

La compensación de la fuerza de atracción gravitatoria y la fuerza centrífuga

${\displaystyle -G\frac{M}{r_0^3}\overrightarrow{r_0}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r_0}=0}$

producen el sentido de ingravidez que experimentan los astronautas en una nave espacial

La aceleración $\overrightarrow{a}\text{'}$ del cuerpo en el S.R. no Inercial se puede aproximar a

${\displaystyle \overrightarrow{a}\text{'}\approx -{\omega }^2\overrightarrow{r\text{'}}+3{\omega }^2\frac{\overrightarrow{r\text{'}}·\overrightarrow{r_0}}{r_0^2}\overrightarrow{r_0}-2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}-\overrightarrow{\omega }\times \overrightarrow{\omega }\times \overrightarrow{r}\text{'}}$

Restringiendo el movimiento del cuerpo al plano de la órbita, se calculan los productos vectoriales de los vectores:

${\displaystyle \{\begin{array}{l}\overrightarrow{r\text{'}}=x\text{'}\widehat{i}+y\text{'}\widehat{j}\\ \overrightarrow{\omega }=\omega \widehat{k}\\ \overrightarrow{v}\text{'}=v_{x\text{'}}\widehat{i}+v_{y\text{'}}\widehat{j}\\ \overrightarrow{r_0}=r_0\widehat{i}\end{array}}$

Resultando el sistema de ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^{2}x\text{'}}{d{t}^2}=3{\omega }^{2}x\text{'}+2\omega \frac{dy\text{'}}{dt}\\ \frac{d^{2}y\text{'}}{d{t}^2}=-2\omega \frac{dx\text{'}}{dt}\end{array}}$

Derivando la primera ecuación diferencial, y sustituyendo la segunda en la primera, desacoplamos el sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{d^{2}x\text{'}}{d{t}^2}\right)+{\omega }^2\frac{dx\text{'}}{dt}=0\\ \frac{d^2{v}_{x\text{'}}}{d{t}^2}+{\omega }^2{v}_{x\text{'}}=0\end{array}}$

Tenemos una ecuación diferencial cuya solución es similar a la de un Movimiento Armónico Simple (MAS) pero en la velocidad (no en la posición)

v_x’=Asin(ωt)+Bcos(ωt)

Los coeficientes A, B, se determinan a partir de las condiciones iniciales:

${\displaystyle t=0\{\begin{array}{l}x\text{'}=x_0^{\text{'}}\\ y\text{'}=y_0^{\text{'}}\end{array}\{\begin{array}{l}{v}_{0x\text{'}}=u\cos \alpha \\ v_{0y\text{'}}=u\cos \alpha \end{array}\{\begin{array}{l}{\left(\frac{d{v}_{x\text{'}}}{dt}\right)}_0=3{\omega }^2{x}_0^{\text{'}}+2\omega v_{0y\text{'}}\\ {\left(\frac{d{v}_{y\text{'}}}{dt}\right)}_0=-2\omega v_{0x\text{'}}\end{array}}$

El resultado es

${\displaystyle v_{x\text{'}}=\left(3\omega x_0^{\text{'}}+2v_{0y\text{'}}\right)\sin (\omega t)+v_{0x\text{'}}\cos (\omega t)}$

Como v_x'=dx'/dt, integramos de nuevo, para determinar x' en función de t

${\displaystyle x\text{'}=4x_0^{\text{'}}+2\frac{v_{0y\text{'}}}{\omega }-\left(3x_0^{\text{'}}+2\frac{v_{0y\text{'}}}{\omega }\right)\cos (\omega t)+\frac{v_{0x\text{'}}}{\omega }\sin (\omega t)}$

Integramos la segunda ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d{v}_{y\text{'}}}{dt}=-2\omega v_{x\text{'}}\hfill \\ \frac{d{v}_{y\text{'}}}{dt}=-2\omega \left\{\left(3\omega x_0^{\text{'}}+2v_{0y\text{'}}\right)\sin (\omega t)+v_{0x\text{'}}\cos (\omega t)\right\}\hfill \\ v_{y\text{'}}=v_{0y\text{'}}-2\left\{\left(3\omega x_0^{\text{'}}+2v_{0y\text{'}}\right)\left(1-\cos (\omega t)\right)+v_{0x\text{'}}\sin (\omega t)\right\}\hfill \end{array}}$

Se integra de nuevo, con la condición inicial de que y’=y’₀, en el instante t=0.

${\displaystyle y\text{'}=y_0^{\text{'}}-2\frac{v_{0x\text{'}}}{\omega }-\left(6\omega x_0^{\text{'}}+3v_{0y\text{'}}\right)t+2\left(3x_0^{\text{'}}+2\frac{v_{0y\text{'}}}{\omega }\right)\sin (\omega t)+2\frac{v_{0x\text{'}}}{\omega }\cos (\omega t)}$

Las expresiones de x'(t), y'(t), son las ecuaciones paramétricas de la trayectoria de un cuerpo que se mueve en las proximidades de una nave espacial situada en el origen de un S. R. no inercial. Nos permitirá describir el movimiento relativo de un cuerpo que es lanzado x'₀=0, y'₀=0, desde la nave espacial, la de un módulo que se va a acoplar a la nave espacial o de un astronuata que durante su paseo espacial pretende regresar a la nave y que por tanto, parten de una posición inicial x'₀≠0, y'₀≠0 en el instante t=0.

Las expresiones de x' e y' en función del tiempo t se escriben

${\displaystyle \begin{array}{l}x\text{'}-x_c^{\text{'}}=-A\cos (\omega t)+B\sin (\omega t)\\ y\text{'}-y_c^{\text{'}}=2B\cos (\omega t)+2A\sin (\omega t)\end{array}\}\{\begin{array}{l}B=\frac{v_{0x\text{'}}}{\omega }\\ A=3x_0^{\text{'}}+2\frac{v_{0y\text{'}}}{\omega }\\ x_c^{\text{'}}=4x_0^{\text{'}}+2\frac{v_{0y\text{'}}}{\omega }\\ y_c^{\text{'}}=y_0^{\text{'}}-2\frac{v_{0x\text{'}}}{\omega }-\left(6\omega x_0^{\text{'}}+3v_{0y\text{'}}\right)t\end{array}}$

Eliminando el tiempo t obtenemos la ecuación de la trayectoria

${\displaystyle \begin{array}{l}{\left(x\text{'}-x_c^{\text{'}}\right)}^2+\frac{1}{4}{\left(y\text{'}-y_c^{\text{'}}\right)}^2=A^2+B^2\\ \frac{{\left(x\text{'}-x_c^{\text{'}}\right)}^2}{A^2+B^2}+\frac{1}{4}\frac{{\left(y\text{'}-y_c^{\text{'}}\right)}^2}{A^2+B^2}=1\end{array}}$

La trayectoria es una elipse, centrada en x'_c e y'_c , de semieje mayor $a=2\sqrt{A^2+B^2}$ y semieje menor b=a/2. El centro de la elipse se mueve a lo largo del eje Y' (dirección tangencial) con velocidad

${\displaystyle v_c=-\left(6\omega x_0^{\text{'}}+3v_{0y\text{'}}\right)=-\frac{3}{2}\omega x_c^{\text{'}}}$

Durante un periodo, tiempo que tarda la nave espacial en dar una vuelta completa, 2π/ω el centro de la elipse se desplaza, -3πx'_c

Ejemplos

Se lanza un cuerpo desde el origen O'

La posición inicial del objeto es x'₀=y'₀=0

1. El cuerpo se lanza en la dirección radial (a lo largo del eje X’), v_0y’=0

${\displaystyle \begin{array}{l}x\text{'}=\frac{v_{0x}}{\omega }\text{sin}(\omega t)\\ y\text{'}=\frac{2v_{0x}}{\omega }\cos (\omega t)-\frac{2v_{0x}}{\omega }\end{array}}$

La trayectoria es una elipse centrada en y'_c=-2a

${\displaystyle \frac{x{\text{'}}^2}{a^2}+\frac{{(y+2a)}^2}{{(2a)}^2}=1a=\frac{v_{0x}}{\omega }}$

La nave espacial describe una órbita circular alrededor de la Tierra de 400 km de altura, la velocidad angular de rotación ω es

${\displaystyle m{\omega }^2{r}_0=G\frac{Mm}{r_0^2},\omega =\sqrt{\frac{GM}{r_0^3}}}$

>> sqrt(6.67e-11*5.98e24/((6370+400)*1000)^3)
ans =    0.0011

Se lanza un cuerpo desde la nave espacial con velocidad v_0x'=1 m/s inicial en la dirección radial (eje X'). Representamos su trayectoria durante un periodo o tiempo que tarda la nave espacial en dar una vuelta 2π/ω

w=0.00113; %velocidad angular de rotación
v0x=1; %velocidad inicial a lo largo de la dirección radial
hold on
x=@(t) v0x*sin(w*t)/w; %trayectoria
y=@(t) 2*v0x*(cos(w*t)-1)/w;
fplot(y,x,[0,2*pi/w])
plot(0,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
axis equal
grid on
axis equal
xlabel('Y')
ylabel('X')
title('Se lanza un objeto')



2. El cuerpo se lanza en la dirección tangencial (eje Y’),v_0x'=0

${\displaystyle \begin{array}{l}x\text{'}=\frac{2v_{0y\text{'}}}{\omega }\left(1-\cos (\omega t)\right)\hfill \\ y\text{'}=\frac{4v_{0y\text{'}}}{\omega }\sin (\omega t)-3v_{0y\text{'}}t\hfill \end{array}}$

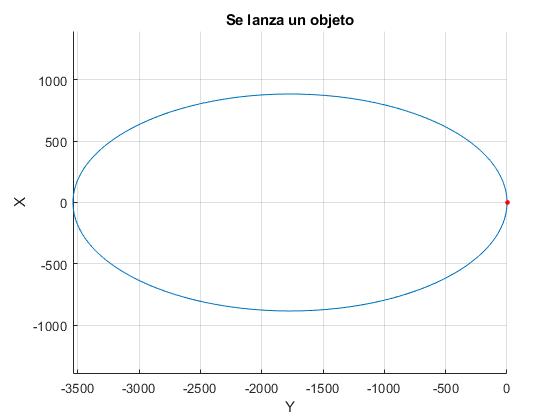
Se lanza un cuerpo desde la nave espacial con velocidad v_0y'=1 m/s inicial en la dirección tangencial (eje Y'). Representamos su trayectoria durante un periodo y medio o tiempo que tarda la nave espacial en dar una vuelta y media (2π/ω)·3/2

w=0.00113; %velocidad angular de rotación
v0y=1; %velocidad inicial a lo largo de la dirección radial
hold on
x=@(t) 2*v0y*(1-cos(w*t))/w; %trayectoria
y=@(t) 4*v0y*sin(w*t)/w-3*v0y*t;
fplot(y,x,[0,(2*pi/w)*3/2])
plot(0,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
axis equal
grid on
axis equal
xlabel('Y')
ylabel('X')
title('Se lanza un objeto')

Encuentros espaciales

La posición inicial del objeto es (x'₀≠0, y'₀≠0) en el instante t=0 y la posición final para que se produzca el encuentro en el instante t_f es (x'₀=0, y'₀=0) el origen donde está situada la nave espacial.

Un astronuata se encuentra en la posición inicial (x'₀, y'₀) durante un paseo espacial y quiere regresar a la nave espacial.

• El astronauta está inicialmente en reposo relativo a la nave espacial v_0x'=0, v_0y'=0

${\displaystyle \begin{array}{l}x\text{'}=x_0^{\text{'}}+3x_0^{\text{'}}\left(1-\cos (\omega t)\right)\hfill \\ y\text{'}=y_0^{\text{'}}-6x_0^{\text{'}}\left(\omega t-\sin (\omega t)\right)\hfill \end{array}}$

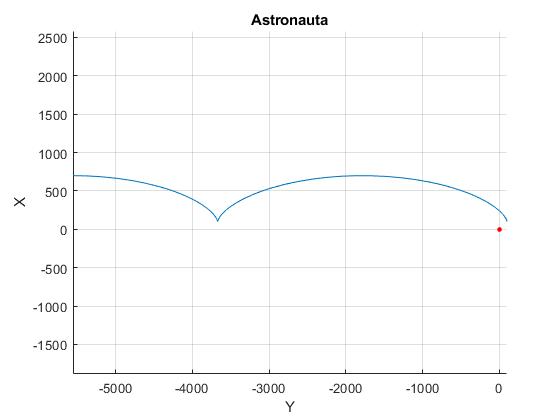
Una nave espacial describe una órbita circular de 400 km de altura, la velocidad angular de rotación es ω=0.00113 rad/s. El astronauta está inicialmente en reposo relativo a la nave espacial en la posición inicial x'₀=y'₀=100 m

Representamos la trayectoria durante un periodo y medio (la nave espacial da vuelta y media a la Tierra)

x0=100; %posición inicial
y0=100; 
w=0.00113; %velocidad angular de rotación
x=@(t) x0+3*x0*(1-cos(w*t)); %trayectoria
y=@(t) y0-6*x0*(w*t-sin(w*t));
hold on
fplot(y,x,[0,(2*pi/w)*3/2])
plot(0,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
axis equal
grid on
axis equal
xlabel('Y')
ylabel('X')
title('Astronauta')





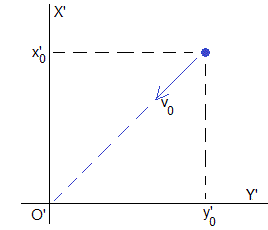
• El astronauta en la posición inicial (x'₀, y'₀) se impulsa con velocidad v₀ en la dirección de la recta que une la posición inicial con el origen donde está situada la nave espacial.

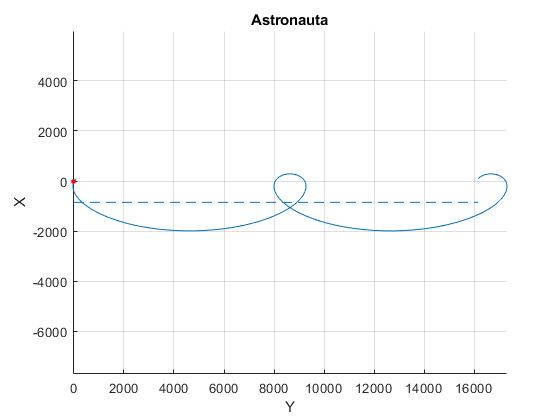
Por ejemplo, la posición inicial es x'₀=y'₀=100 m, la velocidad inicial v₀= 1 m/s, sus componentes son v_0x'=v_0y'=-$\sqrt{2}/2$ m/s. Representamos la trayectoria durante dos periodos o en el tiempo que tarda la nave espacial en dar dos vueltas a la Tierra.

Sobre la trayectoria marcamos la línea x'_c=4x'₀+2v_0y'/ω en la que se mueve el centro de la elipse que se desplaza con velocidad v_c=3x'_c/2=-1.44 m/s. Durante un periodo se desplaza Δx_c=-3πx'_c=8.02 km

x0=100; %posición inicial
y0=100; 
w=0.00113; %velocidad angular de rotación
v0x=-sqrt(2)/2; %velocidad inicial
v0y=-sqrt(2)/2;
%trayectoria
x=@(t) 4*x0+2*v0y/w-(3*x0+2*v0y/w)*cos(w*t)+v0x*sin(w*t)/w;
y=@(t) y0-2*v0x/w-(6*w*x0+3*v0y)*t+2*(3*x0+2*v0y/w)*sin(w*t)+2*v0x*cos(w*t)/w;
hold on
fplot(y, x,[0,2*(2*pi/w)])
plot(0,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
xc=4*x0+2*v0y/w;
line([0,y(2*(2*pi/w))],[xc,xc], 'lineStyle','--')
hold off
grid on
axis equal
xlabel('Y')
ylabel('X')
title('Astronauta')



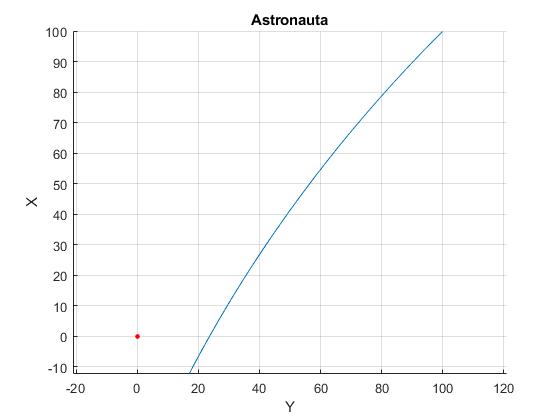
Vamos a examinar con más detalle el movimiento del astronuata en las proximidades de la nave espacial. Comprobaremos que la trayectoria del astronauta no pasa por el origen O', pasa a una distancia d mínima de la nave espacial. Representamos la trayectoria durante un tiempo $100\sqrt{2}$≈142 s

x0=100; %posición inicial
y0=100; 
w=0.00113; %velocidad angular de rotación
v0x=-sqrt(2)/2; %velocidad inicial
v0y=-sqrt(2)/2;
%trayectoria
x=@(t) 4*x0+2*v0y/w-(3*x0+2*v0y/w)*cos(w*t)+v0x*sin(w*t)/w;
y=@(t) y0-2*v0x/w-(6*w*x0+3*v0y)*t+2*(3*x0+2*v0y/w)*sin(w*t)+
2*v0x*cos(w*t)/w;
hold on
fplot(y, x,[0,142])
plot(0,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
grid on
axis equal
xlabel('Y')
ylabel('X')
title('Astronauta')



Calcularemos la distancia mínima de aproximación, utilizando Math Symbolic de MATLAB, dado que las expresiones son muy largas

• Expresamos la distancia del astronauta al origen $d(t)=\sqrt{x\text{'}{(t)}^2+y\text{'}{(t)}^2}$ en función del tiempo t
• Calculamos su derivada mediante la función diff de MATLAB
• Igualamos la derivada a cero y calculamos una de las posibles raíces de la ecuación transcendente mediante la función vpasolve, que nos devueve un valor numérico en vez de simbólico, que posiblemente no exista

syms x0 y0 v0x v0y w t;
x=4*x0+2*v0y/w-(3*x0+2*v0y/w)*cos(w*t)+v0x*sin(w*t)/w;
y=y0-2*v0x/w-(6*w*x0+3*v0y)*t+2*(3*x0+2*v0y/w)*sin(w*t)+2*v0x*cos(w*t)/w;
dist=sqrt(x^2+y^2);
dist_min=diff(dist,t);
dmin=subs(dist_min,{x0,y0,v0x,v0y,w},{100, 100, -1/sqrt(2),
-1/sqrt(2),0.00113});
td=vpasolve(dmin==0,t,[0,242]);
disp([double(td),double(subs(dist,{x0,y0,v0x,v0y,w,t},
{100, 100, -1/sqrt(2),-1/sqrt(2),0.00113, td}))])

En el instante t=139.1 s el astronauta se encuentra a una distancia de 20.7 m de la nave espacial

  139.1104   20.7045

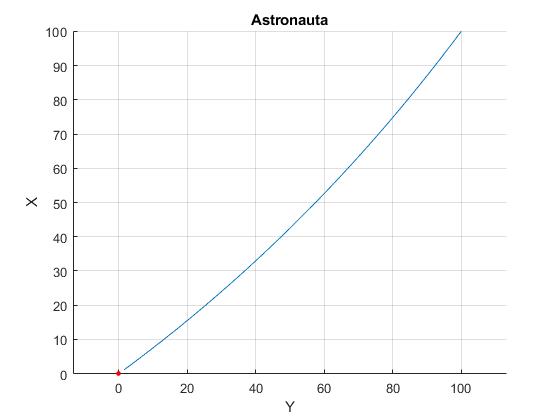
Para que el astronauta llegue a la nave espacial situada en el origen (x'=0, y'=0) en el tiempo t_f=142 s, desde la posición inicial (x'₀, y'₀), despejamos las componentes de la velocidad inicial v_0x' y v_0y' de las ecuaciones paramétricas de la trayectoria, x'(t), y'(t)

${\displaystyle \begin{array}{l}\begin{array}{l}{A}_1{v}_{0x\text{'}}+B_1{v}_{0y\text{'}}=C_1\\ A_2{v}_{0x\text{'}}+B_2{v}_{0y\text{'}}=C_2\end{array}\}\{\begin{array}{l}{A}_1=\frac{\sin (\omega t_f)}{\omega }\\ A_2=-\left(1-\cos (\omega t_f)\right)\frac{2}{\omega }\\ B_1=\left(1-\cos (\omega t_f)\right)\frac{2}{\omega }\\ B_2=-3t_f+\frac{4}{\omega }\sin (\omega t_f)\\ C_1=x_0^{\text{'}}\left(3\cos (\omega t_f)-4\right)\\ C_2=6x_0^{\text{'}}\left(\omega t_f-\sin (\omega t_f)\right)-y_0^{\text{'}}\end{array}\\ \{\begin{array}{l}{v}_{0x\text{'}}=\frac{C_1{B}_2-C_2{B}_1}{A_1{B}_2-A_2{B}_1}\\ v_{0y\text{'}}=\frac{C_2{A}_1-C_1{A}_2}{A_1{B}_2-A_2{B}_1}\end{array}\end{array}}$

x0=100; %posición inicial
y0=100; 
w=0.00113; %velocidad angular de rotación
tf=142; %tiempo

A1=sin(w*tf)/w;
A2=-(1-cos(w*tf))*2/w;
B1=(1-cos(w*tf))*2/w;
B2=-3*tf+4*sin(w*tf)/w
C1=x0*(3*cos(w*tf)-4);
C2=6*x0*(w*tf-sin(w*tf))-y0;
v0x=(C1*B2-C2*B1)/(A1*B2-A2*B1); %velocidad inicial
v0y=(C2*A1-C1*A2)/(A1*B2-A2*B1);

%trayectoria
x=@(t) 4*x0+2*v0y/w-(3*x0+2*v0y/w)*cos(w*t)+v0x*sin(w*t)/w;
y=@(t) y0-2*v0x/w-(6*w*x0+3*v0y)*t+2*(3*x0+2*v0y/w)*sin(w*t)
+2*v0x*cos(w*t)/w;
hold on
fplot(x, y,[0,140])
plot(0,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
hold off
grid on
axis equal
xlabel('Y')
ylabel('X')
title('Astronauta')



>> v0x,v0y
v0x =   -0.6039
v0y =   -0.8119

Para que el encuentro espacial se lleve a cabo con éxito desde una posición inicial dada, no vale que la dirección de la velocidad inicial sea la línea recta que une la posición inicial con el origen

Apolo 11: Encuentro del módulo lunar con el módulo de servicio en la órbita de la Luna

El módulo de servicio (CSM) de la misión Apolo 11 describía una órbita circular 111.12 km por encima de la Luna. Aplicamos la ecuación de la dinámica del movimiento circular para calcular la velocidad angular ω

${\displaystyle m{\omega }^2{r}_0=G\frac{Mm}{r_0^2},\omega =\sqrt{\frac{GM}{r_0^3}}}$

La masa de la Luna es M=7.349·10²² kg y su radio R=1737.4 km. La velocidad angular es ω=8.81·10^-4 rad/s

>> sqrt(6.67e-11*7.349e22/((1737.4+111.12)*1000)^3)
ans =   8.8093e-04

El módulo lunar ascendía desde la superficie de la Luna para acoplarse con el módulo de servicio. Cuando se encontraba en la posición x₀=-27.78 km por debajo e y₀=-55.72 km, se dispone a encontrarse con el módulo de servico en un tiempo de t_f=42 min. Calculamos las componentes de la velocidad inicial (v_0x', v_0y') y dibujamos la trayectoria hasta el módulo de servicio situado en el origen del S.R. no inercial

y0=-55720; %posición inicial
x0=-27780; 
w=8.81e-4; %velocidad angular d erotación
tf=42*60; %tiempo

A1=sin(w*tf)/w;
A2=-(1-cos(w*tf))*2/w;
B1=(1-cos(w*tf))*2/w;
B2=-3*tf+4*sin(w*tf)/w
C1=x0*(3*cos(w*tf)-4);
C2=6*x0*(w*tf-sin(w*tf))-y0;
v0x=(C1*B2-C2*B1)/(A1*B2-A2*B1); %velocidad inicial
v0y=(C2*A1-C1*A2)/(A1*B2-A2*B1);

%trayectoria
x=@(t) 4*x0+2*v0y/w-(3*x0+2*v0y/w)*cos(w*t)+v0x*sin(w*t)/w;
y=@(t) y0-2*v0x/w-(6*w*x0+3*v0y)*t+2*(3*x0+2*v0y/w)*sin(w*t)+
2*v0x*cos(w*t)/w;
hold on
fplot(y, x,[0,42*60])
plot(0,0,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
tt=0:120:42*60;
plot(y(tt),x(tt),'o','markersize',3,'markeredgecolor','k','markerfacecolor','k')
hold off
grid on
axis equal
xlabel('Y')
ylabel('X')
title('Encuentro en la Luna')

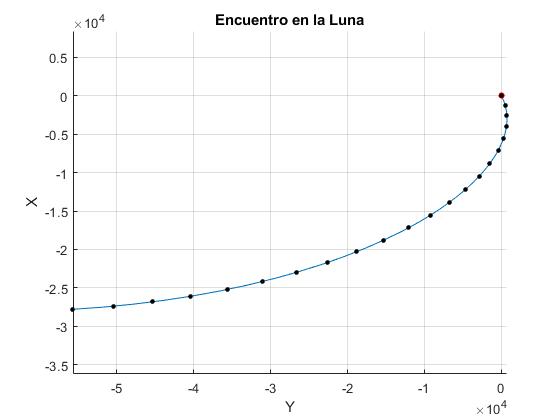
Las componentes de la velocidad inicial del módulo lunar son: v_0x'=2.52 m/s y v_0y'=43.7 m/s relativas al módulo de servicio (CSM). Los puntos de color negro marcan la posición del módulo lunar cada 2 minutos

>> v0x,v0y
v0x =    2.5216
v0y =   43.7115

Referencias

Butikov E. I. Relative motion of orbiting bodies. Am. J. Phys. 69 (1) January 2001, pp. 63-67

Bradley W. Carroll. The delicate dance of orbital rendezvous. Am. J. Phys. 87 (8) August 2019, pp. 627-637

Freedman R. A., Helmy I., Zimmerman P. D. Simplified navigation for self-propelled astronauts. Am. J. Phys. 43 (5) May 1975, pp. 438-440