Datos de la Tierra, Júpiter, Urano y el Sol

Para resolver este problema se precisan los siguientes datos:

• la constante de la Gravitación Universal, G=6.673·10^-11 N²m²/kg²
• la masa del Sol, M_S=1.98·10³⁰ kg,
• la distancia media entre la Tierra y el Sol, r₁=1.496·10¹¹ m
• una Unidad Astronómica, UA=1.496·10¹¹ m
• la masa de la Júpiter, M_J=1.90·10²⁷ kg
• la distancia media entre Júpiter y el Sol, r_J=5.2 UA
• el radio de Júpiter, R_J=6.98·10⁷ m
• radio de influencia del planeta Júpiter, R_e=4.83·10¹⁰ m
• la distancia media entre Urano y el Sol, r₂=19.2 UA

Movimiento de la Tierra, Júpiter y Urano alrededor del Sol

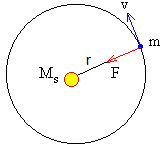
Supondremos que los tres planetas describen órbitas circulares cuyo centro es el Sol. Aplicamos la dinámica de movimiento circular uniforme para obtener la velocidad del planeta v en su movimiento de traslación alrededor del Sol

${\displaystyle G\frac{m{M}_S}{r^2}=m\frac{v^2}{r}}$

Despejando la velocidad v del planeta

${\displaystyle v=\sqrt{\frac{G{M}_s}{r}}}$

Trayectoria elíptica desde la Tierra hasta Urano

En la figura, se muestra el Sol (punto de color rojo), se dibujan a escala las órbitas circulares de la Tierra, de Júpiter y de Urano, la trayectoria elíptica que debería seguir una nave espacial lanzada en las proximidades de la Tierra para que llegase al planeta Urano

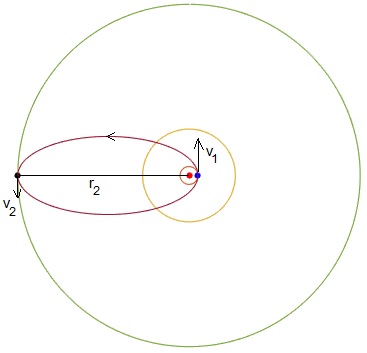
Los datos del problema son:

• r₁=1 UA, radio de la órbita de la Tierra
• r₂=19.2 UA, radio de la órbita de Urano
• a=(r₁+r₂)/2, es el semieje mayor de la elipse
• c=a-r₁=(r₂-r₁)/2, es la semidistancia focal de la elipse
• La excentricidad es ε=c/a=(r₂-r₁)/(r₂+r₁)

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }}$

• En el perihelio θ=0, r₁=d/(1+ε)
• En el afelio θ=π, r₂=d/(1-ε)

${\displaystyle d=\left(\frac{r_1+r_2}{2}\right)\left(1-{\epsilon }^2\right)}$

Se trata de una trayectoria elíptica de excentricidad ε=0.901 y parámetro d=1.901 UA

El código para dibujar parte de la figura es

r2=19.2; %radio de Urano, Unidades Astronómicas 1.496·10^8 m
r1=1; %radio de la órbita de la Tierra
rJ=5.2; %radio de la órbita de Júpiter
hold on
plot (0,0,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
fplot(@(x) r1*cos(x),@(x) r1*sin(x),[0,2*pi])
fplot(@(x) rJ*cos(x),@(x) rJ*sin(x),[0,2*pi])
plot (rT,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
fplot(@(x) r2*cos(x),@(x) r2*sin(x),[0,2*pi])
plot (-r2,0,'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
ex=(r2-r1)/(r2+r1); %excentricidad
d=(r2+r1)*(1-ex^2)/2; %parámetro d
r=@(x) d./(1+ex*cos(x)); %trayectoria
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi])
hold off
axis equal
axis off

Aplicando la constancia del momento angular y de la energía (la fuerza de atracción es central y conservativa), calculamos la velocidad v₁ de la nave espacial en el perihelio (proximidades de la Tierra) r₁ para que llegue a Urano

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_1^2-G\frac{M_{S}m}{r_1}=\frac{1}{2}m{v}_2^2-G\frac{M_{S}m}{r_2}\hfill \\ m{r}_1{v}_1=m{r}_2{v}_2\hfill \end{array}}$

Despejamos v₁

${\displaystyle v_1=\sqrt{2G{M}_s\frac{r_2}{r_1(r_1+r_2)}}}$

Con los datos de r₁=1 UA y r₂=19.2 UA, obtenemos v₁=40 966 m/s

Como la velocidad de la Tierra en su órbita alrededor del Sol es 29 712 m/s, tendremos que dar a la nave espacial un impulso que la proporcione una velocidad adicional de 40 966-29 712=11 254 m/s.

El tiempo que tardaría en llegar a Urano es medio periodo

${\displaystyle P^2=\frac{4{\pi }^2{a}^3}{G{M}_s}}$

P=32.2 años. El tiempo de viaje sería 16.1 años

Vamos a ver como se puede reducir sustancialmente el tiempo de viaje utilizando el campo gravitatorio del planeta Júpiter

Calculamos la intersección de la órbita elíptica de la nave espacial con la órbita circular de Júpiter.

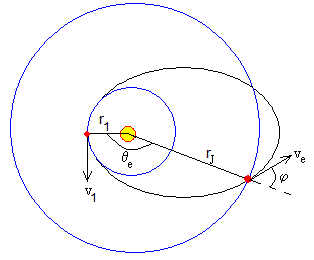
En la ecuación de la trayectoria en coordenadas polares ponemos r=r_J y despejamos el ángulo θ.

${\displaystyle {\theta }_e=\arccos \left(\frac{1}{\epsilon }\left(\frac{d}{r_J}-1\right)\right)}$

θ_e=2.352 (135°)

Como la energía E es constante en todos los puntos de la trayectoria, obtenemos la velocidad v_e de la nave espacial en dicha posición de encuentro

${\displaystyle \frac{1}{2}m{v}_1^2-G\frac{M_{S}m}{r_1}=\frac{1}{2}m{v}_e^2-G\frac{M_{S}m}{r_J}}$

v₁ es la velocidad la nave espacial en las proximidades de la Tierra. De la constancia del momento angular L obtenemos el ángulo φ entre le vector velocidad y la dirección radial (la que une el Sol con el planeta Júpiter)

mr₁v₁=mv_er_J·sinφ

La velocidad y el ángulo son: v_e=15 879 m/s y φ=0.52 (30º)

Tiempo de viaje hasta Júpiter

Utilizamos la ecuación de Kepler

Dada la posición angular θ, determinamos el ángulo E mediante las relaciones

${\displaystyle \sin E=\frac{\sqrt{1-{\epsilon }^2}\sin \theta }{1+\epsilon \cos \theta }\cos E=\frac{\epsilon +\cos \theta }{1+\epsilon \cos \theta }}$

Dependiendo del signo del seno y del coseno, se determina el cuadrante y se calcula el ángulo E. Sustituyendo en la ecuación de Kepler, obtenemos M_e

${\displaystyle M_e=E-\epsilon \sin E}$

Conocido M_e, obtenemos el tiempo

${\displaystyle t=\frac{M_e}{2\pi }P{P}^2=\frac{4{\pi }^2}{G{M}_s}{a}^3}$

Donde M_S es la masa del Sol. La duración del viaje desde las proximidades de la Tierra hasta Júpiter es de 1.245 años

Elaboramos un script para realizar los cálculos de v₁, v_e y el ángulo φ, véase la figura más arriba

MS=1.98e30; %masa del Sol
UA=1.496e11; %unidad astronómica
G=6.67e-11; %constante G
r2=19.2; %radio de Urano, 
r1=1; %radio de la órbita de la Tierra
rJ=5.2; %radio de la órbita de Júpiter

v1=sqrt(2*G*MS*r2/((r1+r2)*r1*UA)); %velocidad de la nave en la Tierra
ve=sqrt(v1^2-2*G*MS/(r1*UA)+2*G*MS/(rJ*UA)); %velocidad cuando llega a Júpiter
phi=asin(r1*v1/(ve*rJ)); %ángulo de la velocidad
ex=(r2-r1)/(r2+r1); %excentricidad
d=(r2+r1)*(1-ex^2)/2;
th=acos((d/rJ-1)/ex); %intersección de la trayectoria con la órbita de Júpiter
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
    E=2*pi+E;
end
t=(E-ex*s_E)*((r1+r2)*UA/2)^(3/2)/sqrt(G*MS);
disp(t/(365*24*3600)) %tiempo en años

   1.2452
>> v1
v1 =   4.0966e+04
>> ve
ve =   1.5879e+04
>> phi
phi =    0.5191

Completamos el script para dibujar la trayectoria elíptica de la nave espacial desde la Tierra hasta las proximidades de Júpiter

...
hold on
plot (0,0,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
fplot(@(x) r1*cos(x),@(x) r1*sin(x),[0,2*pi])
fplot(@(x) rJ*cos(x),@(x) rJ*sin(x),[0,2*pi])
plot (r1,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
fplot(@(x) r2*cos(x),@(x) r2*sin(x),[0,2*pi])
plot (-r2,0,'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
th_j=acos((d/rJ-1)/ex); %corte con la órbita de Urano
r=@(x) d./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi],'lineStyle','--')
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,th_j])
 
hold off
axis equal
axis off

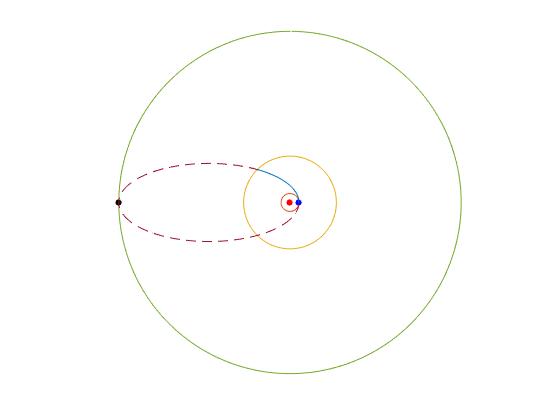
Movimiento de la nave espacial en la esfera de influencia del planeta Júpiter

La nave espacial entra en la esfera de influencia del planeta Júpiter de radio R_e=4.83·10¹⁰ m. Supondremos que la energía potencial debida a la fuerza de atracción del Sol es prácticamente constante en todos los puntos de dicha esfera, por lo que la trayectoria ulterior de la nave espacial viene determinada exclusivamente por la fuerza de atracción del planeta Júpiter, la velocidad inicial y su dirección en el momento en el que entra en dicha esfera de influencia.

Nos situaremos por tanto, en un Sistema de Referencia ligado al planeta Júpiter, calculamos la velocidad inicial y su dirección en este Sistema de Referencia.

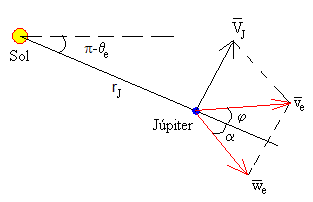
Sea $\overrightarrow{v_e}$ es la velocidad de la nave espacial medida en el S.R. ligado al Sol que forma un ángulo φ con la dirección radial, $\overrightarrow{V_J}$ es la velocidad del planeta Júpiter alrededor del Sol. La velocidad $\overrightarrow{w_e}$ de la nave espacial respecto de un S.R. ligado a Júpiter es

${\displaystyle \overrightarrow{w_e}=\overrightarrow{v_e}-\overrightarrow{V_J}}$

Descomponemos las velocidades, en la dirección radial (Sol-Júpiter) y en la dirección perpendicular a la radial.

w_e·sinα=v_e·sinφ-V_J
w_e·cosα=v_e·cosφ

Continuando con los datos del apartado anterior, calculamos la velocidad de la nave espacial w_e=14 718 m/s  y su dirección α=-0.36 (-20.5°) respecto de la recta que une el Sol con Júpiter, medidos en el S.R. ligado a este planeta.

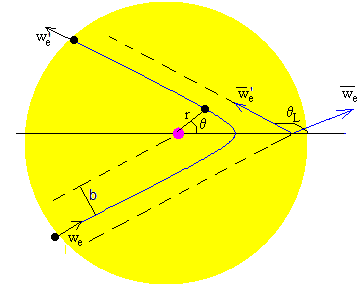
Conocida la energía $E=\frac{1}{2}m{w}_e^2$ y el momento angular L=mbw_e, la ecuación de la trayectoria hiperbólica de la nave espacial en la esfera de influencia de Júpiter es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta } \epsilon =\sqrt{1+\frac{b^2{w}_e^4}{G^2{M}_J^2}}d=\frac{b^2{w}_e^2}{G{M}_J}}$

Como observamos en una trayectoria hiperbólica, solamente hay un cambio en la dirección de la velocidad de $\overrightarrow{w_e}$ a $\overrightarrow{w_e^{\text{'}}}$, pero no en su módulo

El ángulo que forma la dirección final de la velocidad se calcula poniendo r→∞, en la ecuación de la trayectoria,

${\displaystyle {\theta }_L=\arccos \frac{-1}{\epsilon }}$

El ángulo que forma la dirección inicial y la dirección final de la velocidad es 2θ_L-π tal como se aprecia en la figura.

Una vez que la nave espacial ha salido de la esfera de influencia del planeta Júpiter, nos situamos en el Sistema de Referencia ligado al Sol.

El eje de la hipérbola hay que girarlo un cierto ángulo para que la velocidad inicial $\overrightarrow{w_e}$ forme un ángulo α con la recta que une el Sol con el planeta Júpiter, tal como se muestra en la figura. La velocidad final $\overrightarrow{w_e^{\text{'}}}$ formará un ángulo α'=2θ_L-π+α con dicha dirección.

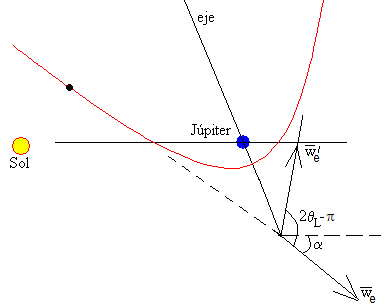
La velocidad final $\overrightarrow{v_e^{\text{'}}}$ de la nave espacial será la suma vectorial

${\displaystyle \overrightarrow{v_e^{\text{'}}}=\overrightarrow{w_e^{\text{'}}}+\overrightarrow{V_J}}$

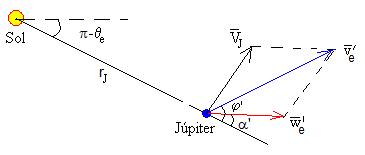
Descomponemos las velocidades, en la dirección radial (Sol-Júpiter) y en la dirección perpendicular a la radial.

${\displaystyle \{\begin{array}{l}{v}_e^{\text{'}}\sin \phi \text{'}=w_e^{\text{'}}\sin \alpha \text{'}+V_J\\ v_e^{\text{'}}\cos \phi \text{'}=w_e^{\text{'}}\cos \alpha \text{'}\end{array}}$

Vamos a determinar el valor del parámetro de impacto b para que la transferencia de velocidad sea máxima, es decir, para que los vectores $\overrightarrow{w_e^{\text{'}}}$ y $\overrightarrow{V_J}$, sean paralelos de modo que, la velocidad final de la nave espacial al salir de la esfera de influencia de Júpiter sea v'_e=w'_e+V_J

Para que sean paralelos, el ángulo α'=π/2 (90°). Pero α'=2θ_L-π+α, por lo que, θ_L=3π/4+α/2

${\displaystyle \begin{array}{l}\cos {\theta }_L=\left(-\frac{\sqrt{2}}{2}\cos \left(\frac{\alpha }{2}\right)+\frac{\sqrt{2}}{2}\sin \left(\frac{\alpha }{2}\right)\right)\\ \frac{1}{\epsilon }=\frac{\sqrt{2}}{2}\left(\cos \left(\frac{\alpha }{2}\right)-\sin \left(\frac{\alpha }{2}\right)\right)\\ \epsilon =\sqrt{1+\frac{b^2{w}_e^4}{G^2{M}_J^2}}\end{array}}$

Con los datos α=-0.36 (-20.5°), w'_e=w_e=14 718 m/s, y V_J=13 029 m/s, obtenemos

• Velocidad final, v’_e=14 718+13 029=27 747 m/s
• Excentricidad, ε=1.22
• Parámetro de impacto, b=5.82·R_J
• Parámetro, d=4.04·R_J

Completamos el script anterior añadiéndole el movimiento de la nave espacial alrededor de Júpiter, se ha tomado como unidad el radio de Júpiter

...
%movimiento alrededor de Júpiter
MJ=1.90e27; %masa de Júpiter
RJ=6.98e7; %radio de Júpiter

VJ=sqrt(G*MS/(5.2*UA)); %velocidad de Júpiter
we=sqrt((ve*sin(phi)-VJ)^2+(ve*cos(phi))^2);
alfa=atan((ve*sin(phi)-VJ)/(ve*cos(phi)));
ex=1/((cos(alfa/2)-sin(alfa/2))*sin(pi/4));
b=sqrt(ex^2-1)*G*MJ/(we^2*RJ);
 
%trayectoria
beta=acos(-1/ex); %asíntota
d=RJ*b^2*we^2/(G*MJ); %en unidades del radio de Júpiter
r=@(x) d./(1+ex*cos(x));
figure
hold on
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[-beta+pi/20,beta-pi/20])
xb=b*ex/sqrt(ex^2-1);
line([xb,-20],[0,(xb+20)*tan(beta)],'lineStyle','--', 'color','k')
line([xb,-20],[0,-(xb+20)*tan(beta)],'lineStyle','--', 'color','k')
line([0,-20],[0,-20*tan(beta)],'lineStyle','--', 'color','k')
%origen, centro de fuerzas
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %Júpiter
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Movimiento alrededor de Júpiter')

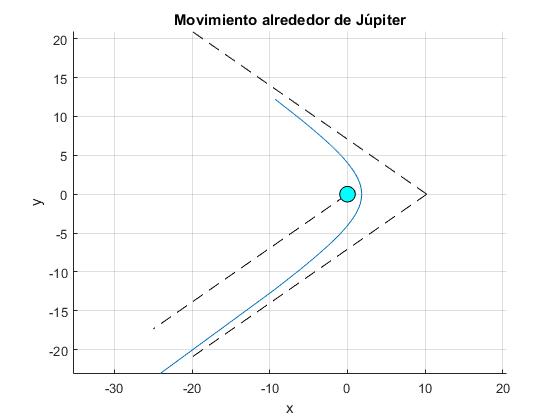
El parámetro de impacto b es la distancia entre las dos rectas paralelas

La distancia mínima de acercamiento a Júpiter es r_m=d/(1+ε)=1.82R_J. La nave espacial no choca con el planeta, r_m>R_J

Empleando la ecuación de Kepler calculamos el tiempo que tarda la nave espacial en atravesar la esfera de infuenecia de Júpiter, que será el doble del empleado en llegar a la distancia más próxima θ=0

Conocida la posición angular θ_e de la nave espacial cuando entra en la esfera de influencia R_e=692·R_J de Júpiter

${\displaystyle {\theta }_e=\arccos \left(\frac{d/R_e-1}{\epsilon }\right)}$

Calculamos el ángulo F

${\displaystyle \tanh \left(\frac{F}{2}\right)=\sqrt{\frac{\epsilon -1}{\epsilon +1}}\tan \left(\frac{\theta }{2}\right)}$

La ecuación de Kepler para trayectorias hiperbólicas nos proporciona el instante t en el que el satélite alcanza la posición θ. Donde M_J es la masa del planeta Júpiter

${\displaystyle \epsilon \sinh F-F={({\epsilon }^2-1)}^{3/2}\frac{G^2{M}_J^2{m}^3}{L^3}t}$

Añadimos las siguientes líneas de código

...
Re=691.8; %radio de influencia en radios de Júpiter
th=acos((d/Re-1)/ex);
F=2*atanh(sqrt((ex-1)/(ex+1))*tan(th/2));
t=(ex*sinh(F)-F)*(we*b*RJ)^3/((ex^2-1)^(3/2)*(G*MJ)^2);
disp(2*t/(24*3600)) %tiempo en días

El tiempo empleado en recorrer la esfera de influencia de Jupiter, en días es

   72.3311

Movimiento hacia Urano

La nave espacial sale de la esfera de influencia de Júpiter con velocidad v’_e=27 747 m/s, su distancia al Sol es aproximadamente igual a r_J=7.78·10¹¹ m, radio de la órbita de Júpiter. La nave espacial se mueve bajo acción de fuerza de atracción solar. La energía y el momento angular son

${\displaystyle E=\frac{1}{2}mv{\text{'}}^2-G\frac{M_{S}m}{r_J}}$

L=mv’_er_J·sinφ’

Con φ’=π/2 (90°) cuando los vectores $\overrightarrow{w_e^{\text{'}}}$ y $\overrightarrow{V_J}$, están alineados

La trayectoria es una hipérbola E>0. La nave espacial se aleja de Júpiter bajo la acción del campo gravitatorio del Sol, camino hacia Urano.

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }\epsilon =\sqrt{1+\frac{2L^{2}E}{m^3{G}^2{M}^2}}d=\frac{L^2}{GM{m}^2}}$

La excentricidad es ε=3.53 y el parámetro d=23.58 Unidades Astronómicas

Se trata de una trayectoria hiperbólica cuya distancia mínima de acercamiento al Sol es el radio de la órbita de Júpiter r_J, en la posición angular θ=0, y llega a Urano cuando su posición angular es θ_U

${\displaystyle {\theta }_u=\arccos \left(\frac{d/r_2-1}{\epsilon }\right)}$

Para determinar el tiempo de viaje entre Júpiter y Urano, conocido θ, calculamos el ángulo F

${\displaystyle \tanh \left(\frac{F}{2}\right)=\sqrt{\frac{\epsilon -1}{\epsilon +1}}\tan \left(\frac{\theta }{2}\right)}$

La ecuación de Kepler para trayectorias hiperbólicas nos proporciona el instante t en el que el satélite alcanza la posición θ. Donde M_S es la masa del Sol

${\displaystyle \epsilon \sinh F-F={({\epsilon }^2-1)}^{3/2}\frac{G^2{M}_S^2{m}^3}{L^3}t}$

Añadimos las siguientes líneas al script para calcular el tiempo t y trazar la trayectoria hiperbólica hasta que corta la órbita de Urano

...
%Trayectoria de Júpiter hacia Urano
v_p=we+VJ; %velocidad final
E_p=v_p^2/2-G*MS/(rJ*UA);
L_p=v_p*(rJ*UA);
ex=sqrt(1+2*L_p^2*E_p/(G*MS)^2);
d=L_p^2/(G*MS*UA); %en unidades astronómicas
%tiempo de viaje
th=acos((d/r2-1)/ex); %corte de la órbita hiperbólica con la circular de Urano
F=2*atanh(sqrt((ex-1)/(ex+1))*tan(th/2));
t=(ex*sinh(F)-F)*L_p^3/((ex^2-1)^(3/2)*(G*MS)^2);
disp(t/(365*24*3600)) %tiempo en años

hold on
plot (0,0,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
fplot(@(x) r1*cos(x),@(x) r1*sin(x),[0,2*pi])
fplot(@(x) rJ*cos(x),@(x) rJ*sin(x),[0,2*pi])
plot (r1,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
fplot(@(x) r2*cos(x),@(x) r2*sin(x),[0,2*pi])
plot (r2*cos(th+th_j),r2*sin(th+th_j),'o','markersize',4,'markeredgecolor'
,'k','markerfacecolor','k')
r=@(x) d./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,th+0.05]) %hiperbólica
hold off
axis equal
axis off

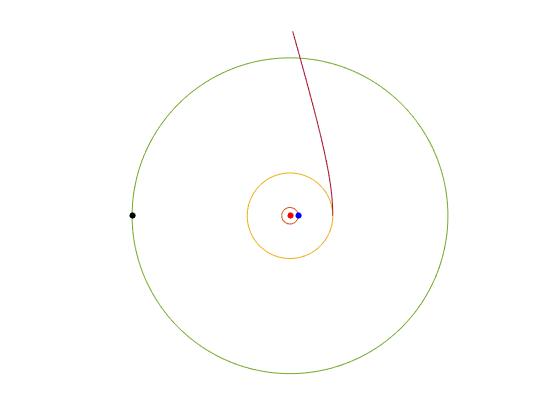
El tiempo de viaje en años entre Júpiter y Urano es

    3.7527

El tiempo de viaje entre la Tierra y Júpiter es 1.245 años, el tiempo de viaje entre Júpiter y Urano, 3.753 años, el tiempo total es de cinco años aproximadamente

Unimos las porciones de código en un solo script para trazar la trayectoria completa de la nave espacial, girando la trayectoria hiperbólica un ángulo igual a la posición angular final de la trayectoria elíptica

MS=1.98e30; %masa del Sol
UA=1.496e11; %unidad astronómica
G=6.67e-11; %constante G
r2=19.2; %radio de Urano, 
r1=1; %radio de la órbita de la Tierra
rJ=5.2; %radio de la órbita de Júpiter

v1=sqrt(2*G*MS*r2/((r1+r2)*r1*UA)); %velocidad de la nave en la Tierra
ve=sqrt(v1^2-2*G*MS/(r1*UA)+2*G*MS/(rJ*UA)); %velocidad cuando llega a Júpiter
phi=asin(r1*v1/(ve*rJ)); %ángulo de la velocidad
ex=(r2-r1)/(r2+r1); %excentricidad
d=(r2+r1)*(1-ex^2)/2;
th=acos((d/rJ-1)/ex); %intersección de la trayectoria con la órbita de Júpiter
c_E=(ex+cos(th))/(1+ex*cos(th));
s_E=sqrt(1-ex^2)*sin(th)/(1+ex*cos(th));
E=atan2(s_E,c_E);
if E<0
    E=2*pi+E;
end
t=(E-ex*s_E)*((r1+r2)*UA/2)^(3/2)/sqrt(G*MS);
disp(t/(365*24*3600)) %tiempo en años

hold on
plot (0,0,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
fplot(@(x) r1*cos(x),@(x) r1*sin(x),[0,2*pi])
fplot(@(x) rJ*cos(x),@(x) rJ*sin(x),[0,2*pi])
plot (r1,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
fplot(@(x) r2*cos(x),@(x) r2*sin(x),[0,2*pi])
plot (-r2,0,'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
r=@(x) d./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,2*pi],'lineStyle','--')
th_j=acos((d/rJ-1)/ex); %intersección de la trayectoria con la órbita de Júpiter
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,th_j])
 
hold off
axis equal
axis off


%movimiento alrededor de Júpiter
MJ=1.90e27; %masa de Júpiter
RJ=6.98e7; %radio de Júpiter

VJ=sqrt(G*MS/(5.2*UA)); %velocidad de Júpiter
we=sqrt((ve*sin(phi)-VJ)^2+(ve*cos(phi))^2);
alfa=atan((ve*sin(phi)-VJ)/(ve*cos(phi)));
ex=1/((cos(alfa/2)-sin(alfa/2))*sin(pi/4));
b=sqrt(ex^2-1)*G*MJ/(we^2*RJ);
 
%trayectoria
beta=acos(-1/ex); %asíntota
d=RJ*b^2*we^2/(G*MJ); %en unidades del radio de Júpiter
r=@(x) d./(1+ex*cos(x));
figure
hold on
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[-beta+pi/20,beta-pi/20])
xb=b*ex/sqrt(ex^2-1);
line([xb,-20],[0,(xb+20)*tan(beta)],'lineStyle','--', 'color','k')
line([xb,-20],[0,-(xb+20)*tan(beta)],'lineStyle','--', 'color','k')
%origen, centro de fuerzas
ang=(1:360)*pi/180;
fill(cos(ang),sin(ang),'c') %Júpiter
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Movimiento alrededor de Júpiter')

%tiempo de viaje
Re=691.8; %radio de influencia en radios de Júpiter
th=acos((d/Re-1)/ex);
F=2*atanh(sqrt((ex-1)/(ex+1))*tan(th/2));
t=(ex*sinh(F)-F)*(we*b*RJ)^3/((ex^2-1)^(3/2)*(G*MJ)^2);
disp(2*t/(24*3600)) %tiempo en días

%Trayectoria de Júpiter hacia Urano
v_p=we+VJ; %velocidad final
E_p=v_p^2/2-G*MS/(rJ*UA);
L_p=v_p*(rJ*UA);
ex=sqrt(1+2*L_p^2*E_p/(G*MS)^2);
d=L_p^2/(G*MS*UA); %en unidades astronómicas
%tiempo de viaje
th=acos((d/r2-1)/ex); %corte con la órbita hiperbólica con la circular de Urano
F=2*atanh(sqrt((ex-1)/(ex+1))*tan(th/2));
t=(ex*sinh(F)-F)*L_p^3/((ex^2-1)^(3/2)*(G*MS)^2);
disp(t/(365*24*3600)) %tiempo en años

%trayectoria completa
figure
hold on
plot (0,0,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
fplot(@(x) r1*cos(x),@(x) r1*sin(x),[0,2*pi])
fplot(@(x) rJ*cos(x),@(x) rJ*sin(x),[0,2*pi])
plot (r1,0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
fplot(@(x) r2*cos(x),@(x) r2*sin(x),[0,2*pi])
plot (-r2,0,'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
%th_j %corte con la órbita elíptica con la circular de Júpiter
r=@(x) d./(1+ex*cos(x-th_j));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[th_j,th+th_j]) %hiperbólica
%órbita elíptica de la Tierra a Júpiter
ex=(r2-r1)/(r2+r1); %excentricidad
d=(r2+r1)*(1-ex^2)/2;
r=@(x) d./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[0,th_j]) %elíptica
hold off
axis equal
axis off

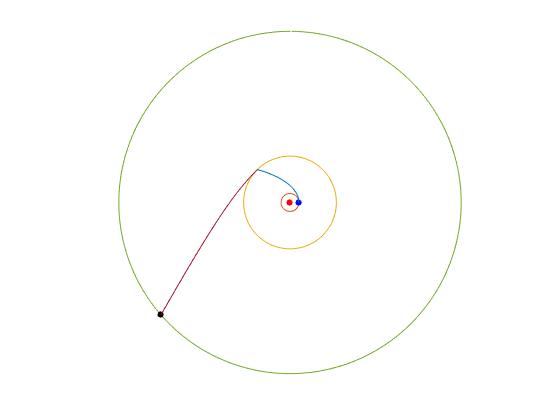
Referencias

Walter Greiner. Cassical Mechanics. Point Particles and Relativity. Springer (2004) pp. 345-355