Movimiento en las proximidades del punto L4
En la página titulada El problema de Euler de los tres cuerpos, estudiamos una situación en la que dos de ellos están fijos en el espacio y una tercera partícula de pequeña masa se mueve en el espacio circundante. Se supone el movimiento de la partícula se confina a un plano que contiene a los cuerpos fijos.
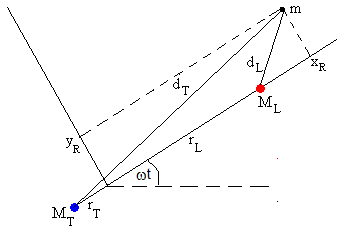
En esta página, resolvemos el problema del movimiento de una cuerpo bajo la acción de dos cuerpos celestes que describen movimientos circulares alrededor del su centro de masas en reposo. Obtuvimos el siguiente sistema de dos ecuaciones diferenciales
Los dos términos en el primer miembro representan las componentes de las fuerzas de Coriolis y centrífuga por unidad de masa.
Ecuaciones del movimiento adimensionales
Establecemos un sistema de unidades tal que la distancia se mide en unidades de la distancia entre la Tierra y la Luna d=rT+rL y el tiempo se mide en unidades tal que un periodo P (tiempo que tarda en dar una vuelta completa la Tierra y la Luna alrededor del c.m.)
Llamando
Simplificando, teniendo en cuenta que α=ML/(ML+MT) y 1-α=MT/(ML+MT)
Constante del movimiento
Empecemos por el caso más simple, el movimiento de una partícula de masa m bajo la fuerza de atracción de un cuerpo fijo en el espacio de masa M, las ecuaciones del movimiento eran
Multiplicamos la primera ecuación por dx/dt y la segunda ecuación por dy/dt y teniendo en cuenta que
Donde el símbolo punto encima de la letra indica derivada respecto del tiempo. Llegamos a
Integramos cada uno de los dos miembros
Donde C es una constante de integración, que es la energía por unidad de masa que se mantiene constante en todos los puntos de la trayectoria
La constante J de Jacobi
Volviendo de nuevo, a las dos ecuaciones diferenciales que describen el movimiento de la partícula en el Sistema de Referencia en rotación. Multiplicamos la primera ecuación por dxR/dt y la segunda ecuación por dyR/dt y sumamos ambas ecuaciones, llegamos a
Integrando de forma similar a caso de una sola fuerza de atracción
J se denomina constante de Jacobi
La constante de Jacobi se expresa en el nuevo sistema de unidades de la siguiente forma
Los tres últimos términos son proporcionales al potencial V(XR, YR) que hemos estudiado en la página titulada Puntos de Lagrange
Resolveremos el sistema de dos ecuaciones diferenciales por el procedimiento numérico
Movimiento en las proximidades del punto L4 del sistema Sol-Júpiter
Consideremos el movimiento de los asteroides troyanos en el sistema formado por el Sol y el planeta Júpiter. Los datos de las masas de los dos cuerpos celestes son:
- Masa de Júpiter, ML=1.898·1027 kg
- Masa del Sol, MT=1.989·1030 kg
- Distancia media entre el Sol y Júpiter, d=5.203 UA=7.7837·1011 m
El parámetro α=ML/(ML+MT)=9.5334·10-4. El periodo P=2π/ω o tiempo que tarda en dar una vuelta completa el sistema formado por el Sol y Júpiter es de P=3.7443·108 s=11.8731 años. Por ejemplo, un tiempo τ=118, equivale a 118/(2π)=18.78 vueltas (ya que en dar una vuelta completa, el sistema Sol-Júpiter emplea un tiempo de 2π en unidades adimensionales). El tiempo real es de 18.78·11.8731=223 años
Las coordenadas del punto L4 de Lagrange son
Tomamos los primeros términos del desarrollo en serie del gradiente de potencial en las proximidades del punto L4. Téngase en cuenta que el gradiente de potencial V es nulo en la posición de equilibrio L4
Hemos calculado las derivadas segundas en la sección Estabilidad la página titulada Puntos de Lagrange. Utilizaremos Math Symbolic de MATLAB para calcular el valor de las derivadas segundas en la posición (a, b) de L4 es decir, los coeficientes c1, c2 y c3
En el código, el parámetro α se representa por la variable simbólica
syms x y k; % k es alfa
V=-(1-k)/sqrt((x+k)^2+y^2)-k/sqrt((x-1+k)^2+y^2)-(x^2+y^2)/2;
Vxx=diff(V,x,2);
c1=subs(Vxx,{x,y},{1/2-k,sqrt(3)/2});
Vyy=diff(V,y,2);
c2=subs(Vyy,{x,y},{1/2-k,sqrt(3)/2});
Vxy=diff(diff(V,x),y);
c3=subs(Vxy,{x,y},{1/2-k,sqrt(3)/2});
>> c1,c2 c1 =-3/4 c2 =-9/4 >> simplify(c3) ans =(3*3^(1/2)*(2*k - 1))/4
El sistema de ecuaciones diferenciales del movimiento se escribe de forma aproximada
Para describir el movimiento aproximado en las cercanías del punto L4(a,b), ensayamos una solución de la forma,
Obtenemos un sistema homogéneo de dos ecuaciones con dos incógnitas A y B
El determinante de los coeficientes deberá ser nulo
Para que el movimiento sea oscilatorio λ2 tiene que ser negativo, es decir, λ un número imaginario. Para que esto ocurra, el discrimiante Δ=1-27α(1-α)≥0
Representamos la función y=1-27x(1-x)
>> fplot(@(x) 1-27*x.*(1-x),[0,1]) >> grid on
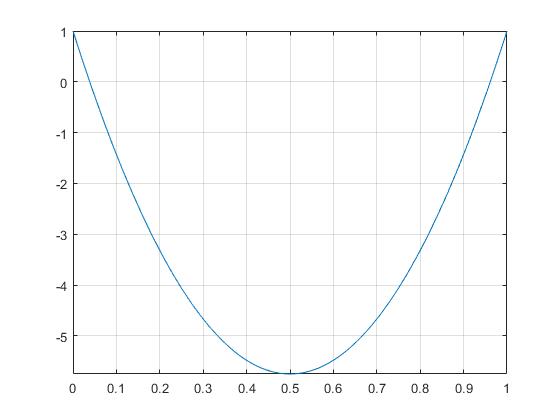
Para α<αc el discriminante Δ es positivo
Cuando se cumple esta condición, las dos raíces imaginarias de la ecuación de cuarto grado son
donde
Como α es pequeño, hacemos la aproximación,
>> syms x; >> taylor(sqrt(1-x),x) ans =- (7*x^5)/256 - (5*x^4)/128 - x^3/16 - x^2/8 - x/2 + 1
Las frecuencias angulares son
Resolvemos el sistema de dos ecuaciones diferenciales por el procedimiento numérico
MT=1.989e30; %masa del Sol
ML=1.898e27; %masa de Júpiter
alfa=ML/(ML+MT);
hold on
x0=[1/2-alfa+0.001,0,sqrt(3)/2+0.002, 0]; %condiciones iniciales
J0=(x0(2)^2+x0(4)^2)/2-(x0(1)^2+x0(3)^2)/2-(1-alfa)/sqrt((x0(1)+alfa)^2+x0(3)^2)-
alfa/sqrt((x0(1)-1+alfa)^2+x0(3)^2);
f=@(t,x) [x(2); 2*x(4)+x(1)-(1-alfa)*(x(1)+alfa)/((x(1)+alfa)^2+x(3)^2)^(3/2)-
alfa*(x(1)-1+alfa)/((x(1)-1+alfa)^2+x(3)^2)^(3/2); x(4); -2*x(2)+x(3)-
(1-alfa)*x(3)/((x(1)+alfa)^2+x(3)^2)^(3/2)-
alfa*x(3)/((x(1)-1+alfa)^2+x(3)^2)^(3/2)];
[t,x]=ode45(f,[0,80*pi],x0);
plot(x(:,1),x(:,3))
J=(x(:,2).^2+x(:,4).^2)/2-(x(:,1).^2+x(:,3).^2)/2-(1-alfa).
/sqrt((x(:,1)+alfa).^2+x(:,3).^2)-alfa./sqrt((x(:,1)-1+alfa).^2+x(:,3).^2);
plot(1/2-alfa,sqrt(3)/2,'ro','markersize',3,'markeredgecolor','r',
'markerfacecolor','r') %L4
hold off
axis square
grid on
xlabel('x')
ylabel('y')
title('Asteriodes troyanos')
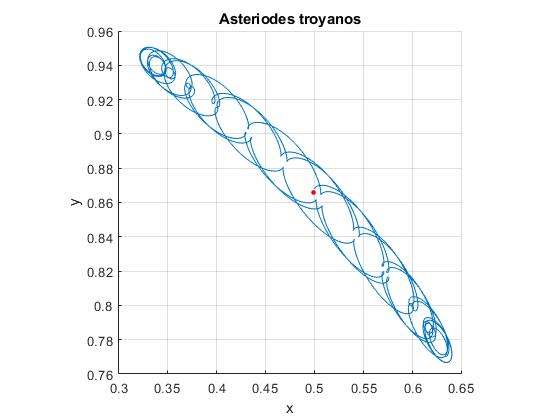
El punto de color rojo señala la posición de L4
Comprobamos que la constante de jacobi, J en unidades adimensionales, se mantiene aproximadamente constante
>> J0 J0 = -1.4995 >> J J = -1.4995 -1.4995 ... -1.4995 -1.4995
Ajuste a la suma de dos funciones armónicas
Utilizamos el script para representar la coordenda XR en función del tiempo τ. Vamos a comprobar que se ajusta a la función
Los datos (τ, XR) proporcionados por el procemiento numérico
MT=1.989e30; %masa del Sol
ML=1.898e27; %masa de Júpiter
alfa=ML/(ML+MT);
hold on
x0=[1/2-alfa+0.001,0,sqrt(3)/2+0.002, 0];
f=@(t,x) [x(2); 2*x(4)+x(1)-(1-alfa)*(x(1)+alfa)/((x(1)+alfa)^2+x(3)^2)^(3/2)-
alfa*(x(1)-1+alfa)/((x(1)-1+alfa)^2+x(3)^2)^(3/2); x(4); -2*x(2)+x(3)-
(1-alfa)*x(3)/((x(1)+alfa)^2+x(3)^2)^(3/2)-alfa*x(3)
/((x(1)-1+alfa)^2+x(3)^2)^(3/2)];
[t,x]=ode45(f,[0,80*pi],x0);
plot(t,x(:,1))
%ajuste
w1=sqrt(27*alfa/4);
w2=1-27*alfa/8;
f=@(a,t) a(1)+a(2)*cos(w1*t+a(3))+a(4)*cos(w2*t+a(4));
error=@(a) sum((x(:,1)-f(a,t)).^2);
a0=[0.5, -0.1, 1.6, 0.01, 1.8]; %valor inicial
af=fminsearch(error,a0);
g=@(t) f(af,t);
fplot(g,[0,80*pi])
legend('e. d.','ajuste','location','southeast')
hold off
grid on
xlabel('x')
ylabel('y')
title('Asteriodes troyanos')
En color azul, la trayectoria, solución del sistema de dos ecuaciones diferenciales. En rosa, el ajuste a la función suma de dos armónicos de frecuencias angulares Ω1 y Ω2 y un término constante
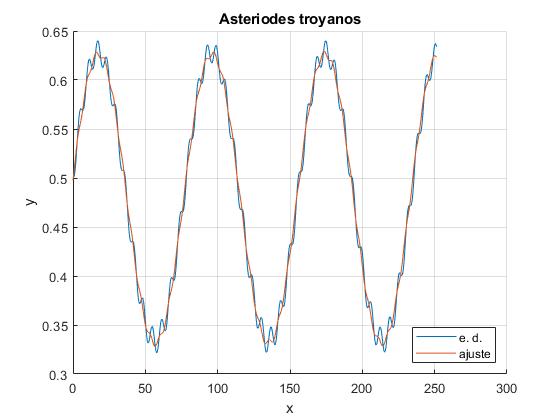
>> af af = 0.4790 -0.1474 1.7213 -0.0034 2.9514
Los valores de los parámetrros de ajuste son: A0=0.4790, A1=-0.1474, φ1=1.7213, A2=-0.0034 y φ2= 2.9514
Trayectoria en el Sistema de Referencia en Rotación y en el Sistema de Referencia Inercial
Resolvemos el sistema de dos ecuaciones diferenciales por el procedimiento numérico
MT=1.989e30; %masa del Sol
ML=1.898e27; %masa de Júpiter
alfa=ML/(ML+MT);
hold on
x0=[1/2-alfa+0.024,0.0778,sqrt(3)/2+0.055, -0.0429];
J0=(x0(2)^2+x0(4)^2)/2-(x0(1)^2+x0(3)^2)/2-(1-alfa)/sqrt((x0(1)+alfa)^2+x0(3)^2)-
alfa/sqrt((x0(1)-1+alfa)^2+x0(3)^2);
f=@(t,x) [x(2); 2*x(4)+x(1)-(1-alfa)*(x(1)+alfa)/((x(1)+alfa)^2+x(3)^2)^(3/2)-
alfa*(x(1)-1+alfa)/((x(1)-1+alfa)^2+x(3)^2)^(3/2); x(4); -2*x(2)+x(3)-
(1-alfa)*x(3)/((x(1)+alfa)^2+x(3)^2)^(3/2)-alfa*x(3)/((x(1)-1+
alfa)^2+x(3)^2)^(3/2)];
[t,x]=ode45(f,[0,80*pi],x0);
plot(x(:,1),x(:,3))
J=(x(:,2).^2+x(:,4).^2)/2-(x(:,1).^2+x(:,3).^2)/2-(1-alfa).
/sqrt((x(:,1)+alfa).^2+x(:,3).^2)-alfa./sqrt((x(:,1)-1+alfa).^2+x(:,3).^2);
plot(1/2-alfa,sqrt(3)/2,'ro','markersize',3,'markeredgecolor','r',
'markerfacecolor','r') %L4
plot(1/2-alfa,-sqrt(3)/2,'ro','markersize',3,'markeredgecolor','r',
'markerfacecolor','r') %L5
hold off
axis square
grid on
xlabel('x')
ylabel('y')
title('Asteriodes troyanos')
Los puntos de color rojo señalan las posiciones de L4 (arriba) y L5 (abajo)
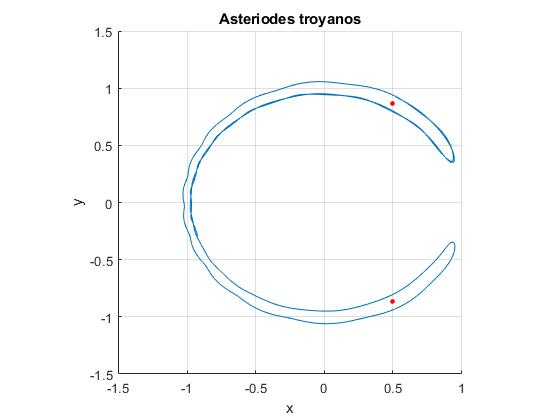
Comprobamos que la constante de Jacobi J en unidades adimensionales, se mantiene aproximadamente constante
J0 = -1.5007 >> J = -1.5007 -1.5007 .... -1.5007 -1.5007
Representamos esta trayectoria en el Sistema de Referencia Inercial. Como hemos demostrado al principio de esta página, la relación entre la posición de la partícula (X,Y) en el sistema inercial y la posición de dicha partícula (XR,YR) en el sistema en rotación, en unidades adimensionales, es
MT=1.989e30; %masa del Sol
ML=1.898e27; %masa de Júpiter
alfa=ML/(ML+MT);
x0=[1/2-alfa+0.024,0.0778,sqrt(3)/2+0.055, -0.0429];
f=@(t,x) [x(2); 2*x(4)+x(1)-(1-alfa)*(x(1)+alfa)/((x(1)+alfa)^2+x(3)^2)^(3/2)
-alfa*(x(1)-1+alfa)/((x(1)-1+alfa)^2+x(3)^2)^(3/2); x(4); -2*x(2)+x(3)-
(1-alfa)*x(3)/((x(1)+alfa)^2+x(3)^2)^(3/2)-alfa*x(3)/((x(1)-1+
alfa)^2+x(3)^2)^(3/2)];
[t,x]=ode45(f,[0,80*pi],x0);
X=x(:,1).*cos(t)-x(:,3).*sin(t);
Y=x(:,1).*sin(t)+x(:,3).*cos(t);
plot(X,Y)
axis square
grid on
xlabel('x')
ylabel('y')
title('Asteriodes troyanos')
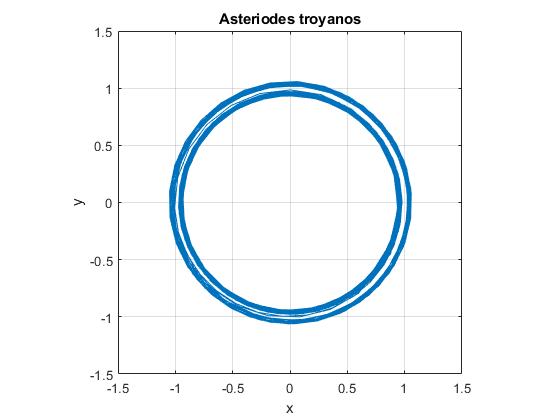
La trayectoria que sigue el asteroide es circular, pasando del exterior al interior en ciertos intervalos de tiempo. El lector pueda apreciar el comportamiento del asteroide en la siguiente animación
Actividades
Se elige
- Representar la trayectoria del asteroide en el Sistema de Referencia en Rotación, activando el botón de radio S. R. Rotación
- Representar la trayectoria del asteroide en el Sistema de Referencia Inercial, activando el botón de radio S. R. Inercial
En la parte inferior, se proporciona el tanto por ciento de error, de la constante J del movimiento. Cuando es mayor que la unidad, el programa se detiene.
Cuando se elige S.R. Inercial, observamos que hacia τ=10, el asteroide se mueve desde la circunferencia exterior hacia la interior, en la que permenece hasta aproximadamente hasta τ=102, que vuelve a la circunferencia exterior
Viaje de la Tierra a la Luna
Supongamos que el sistema formado por la Tierra y la Luna (o por el Sol y Júpiter) se mueven en órbitas circulares alrededor de su centro de masas común.
Datos del sistema Tierra-Luna:
- Masa de la Tierra, MT=5.98·1024 kg
- Radio de la Tierra, RT=6370 km=6.37·106 m
- Masa de la Luna, ML=7.34·1022 kg
- Radio de la Luna, RL=1740 km=1.74·106 m
- Distancia entre la Tierra y la Luna, d=384400 km=384.4·106 m
- Velocidad angular de rotación del sistema Tierra-Luna, ω=2.76·10-6 rad/s
La Tierra y la Luna fijos en el espacio
Primero resolvemos un problema más sencillo. Supongamos que la Tierra y la Luna están fijos en el espacio. Vamos a calcular la velocidad mínima con la que se debe disparar una bala, desde la superficie de la Tierra, a lo largo en la dirección que une los centros de los dos cuerpos celestes, para que llegue a la Luna.
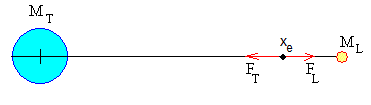
Entre la Tierra y la Luna hay un punto de equilibrio situado a una distancia x del centro de la Tierra. Un objeto de masa m situado en dicho punto experimenta dos fuerzas de atracción iguales y de sentido contrario. Como la masa de la Tierra es mayor que la masa de la Luna, dicho punto xe estará cerca de la Luna.
La posición de equilibrio en la línea que une el centro de la Tierra con el centro de la Luna, se encuentra a xe=345.7 ·106 m del centro de la Tierra.
G=6.67e-11; %constante G
MT=5.98e24; %Masa de la Tierra
ML=7.34e22; %masa de la Luna
RT=6.37e6; %radio de la Tierra
RL=7.34e6; %radio de la Luna
d=384.4e6; %distancia entre sus centros
x=(1:0.5:59)*RT;
F=-G*MT./x.^2+G*ML./(d-x).^2;
plot(x/RT,F/9.8)
grid on
ylim([-0.1,0.05])
xlabel('r/R_T')
ylabel('F/(mg)')
title('Fuerza que ejerce la Tierra y la Luna')
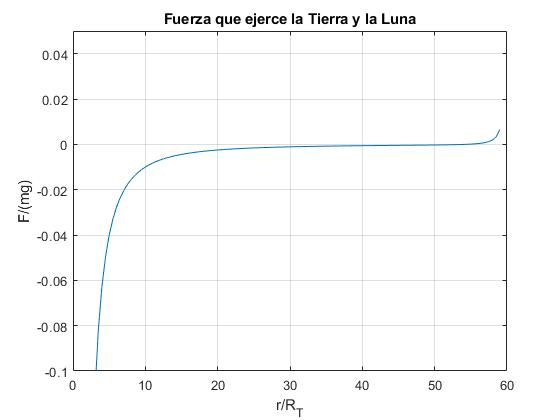
La energía potencial de la partícula bajo la acción de la fuerza de atracción de la Tierra y de la Luna es

Vamos a calcular la velocidad v con la que tenemos que disparar la bala desde la superficie de la Tierra para que llegue al punto de equilibrio xe con una velocidad nula, tal como se aprecia en la figura
La energía de la bala en la superficie de la Tierra x=RT es
La energía de la bala en la posición de equilibrio, es
Poniendo ve=0, y aplicando el principio de conservación de la energía, obtenemos la velocidad mínima de disparo vT=11076.8 m/s
Comparamos esta velocidad, con la velocidad de escape de la superficie de la Tierra únicamente
v=11190.7 m/s
La Tierra y la Luna en movimiento de rotación
En el sistema Tierra-Luna, el eje X pasa por el centro de los dos cuerpos, y el origen se sitúa en el centro de masa del sistema, el centro de la Tierra a la izquierda a una distancia rT=αd, y el centro de la Luna a una distancia rL=(1-α)d
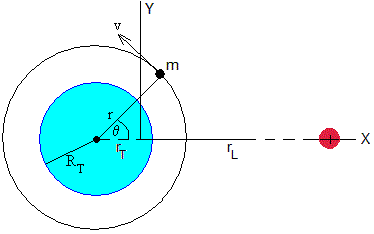
Una nave espacial describe una órbita circular alrededor de la Tierra a una altura h de su superficie a una distancia r de su centro. Aplicando la dinámica del movimiento circular uniforme obtenemos la velocidad v del satélite.
Por ejemplo, un satélite artificial que circunda la Tierra a una altura de h=1000 km o bien r=7.37·106 m lleva una velocidad de v=7356.6 m/s y tarda 1.75 horas en dar una vuelta completa. Un satélite geostacionario que tarda un día en dar una vuelta completa, se encuentra a una altura h=42250.5-3670=38580 km de altura y su velocidad es v=3072.5 m/s
Cuando la nave espacial se encuentra en la posición tal que hace un ángulo θ, con la dirección que une el centro de la Tierra y el centro de la Luna se encienden los cohetes por un breve intervalo de tiempo, dándole una velocidad adicional Δv en dirección tangente a la trayectoria
En el instante t=0, la nave espacial parte de la posición
x0=-rT+r·cosθ
y0= r·sinθ
Con velocidad inicial
v0x=-(v+Δv)·sinθ
v0y=(v+Δv)·cosθ
Donde Δv es el incremento de velocidad proporcionado por los cohetes de la nave de forma casi instantánea.
La posición inicial de la nave se convierte en unidades adimensionales dividiéndola entre d (distancia Tierra-Luna). La velocidad inicial de la nave se convierte en unidades adimensionales dividiéndola entre ωd
Representamos la trayectoria de la nave espacial. La posición del centro de la Tierra en color azul y de la Luna en color rojo
MT=5.98e24; %masa de la Tierra
ML=7.34e22; %masa de la Luna
alfa=ML/(ML+MT);
d=384.4e6; %distancia Tierra-Luna
RT=6.37e6; %radio de la Tierra
w=sqrt(6.67e-11*(ML+MT)/d^3); %velocidad angular de rotación
ang=250*pi/180; %angulo de disparo
h=25480*1000; %altura en metros
inc=1190; %incremento de velocidad
x0=zeros(1,4); %condiciones iniciales
x0(1)=(-alfa*d+(h+RT)*cos(ang))/d;
x0(3)=(h+RT)*sin(ang)/d;
v=sqrt(6.67e-11*MT/(RT+h)); %velocidad de la nave
x0(2)=-(v+inc)*sin(ang)/(w*d);
x0(4)=(v+inc)*cos(ang)/(w*d);
tspan=w*10*24*3600;
f=@(t,x) [x(2); 2*x(4)+x(1)-(1-alfa)*(x(1)+alfa)/((x(1)+alfa)^2+x(3)^2)^(3/2)-
alfa*(x(1)-1+alfa)/((x(1)-1+alfa)^2+x(3)^2)^(3/2); x(4); -2*x(2)+x(3)-
(1-alfa)*x(3)/((x(1)+alfa)^2+x(3)^2)^(3/2)-alfa*x(3)/((x(1)-1+alfa)^2+
x(3)^2)^(3/2)];
J0=(x0(2)^2+x0(4)^2)/2-(x0(1)^2+x0(3)^2)/2-(1-alfa)/sqrt((x0(1)+alfa)^2+x0(3)^2)
-alfa/sqrt((x0(1)-1+alfa)^2+x0(3)^2);
[~,x]=ode45(f,[0,tspan],x0);
hold on
plot(x(:,1),x(:,3))
J=(x(:,2).^2+x(:,4).^2)/2-(x(:,1).^2+x(:,3).^2)/2-(1-alfa)./sqrt((x(:,1)+alfa).^2+
x(:,3).^2)-alfa./sqrt((x(:,1)-1+alfa).^2+x(:,3).^2);
plot(-alfa,0,'bo','markersize',4,'markeredgecolor','b','markerfacecolor','b')
plot(1-alfa,0,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('y')
title('Viaje de la Tierra a la Luna')
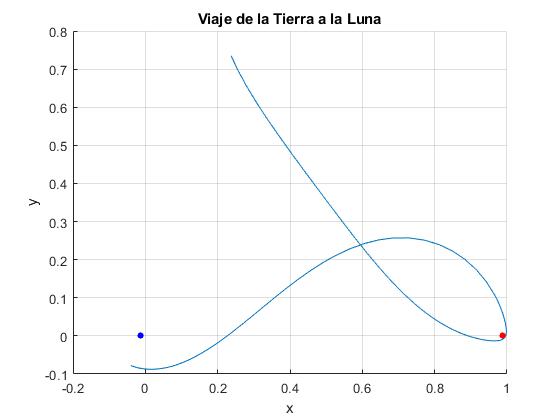
Comprobamos que el valor J se mantiene aproximadamente constante
>> J0 J0 = -1.2936 >> J J = -1.2936 -1.2936 ... -1.2930 -1.2930
Actividades
Se introduce
-
La altura h en km de la órbita circular de la nave espacial sobre la superficie de la Tierra, en el control titulado Altura nave.
Se pulsa el botón titulado Nuevo y a continuación, ►
Se observa el movimiento del sistema Tierra-Luna respecto del Sistema de Referencia Inercial con origen en el centro de masa de ambos cuerpos.
Se observa el movimiento de la nave espacial alrededor de la Tierra y a la vez, la Tierra girando alrededor del c.m. del sistema.
-
La posición angular θ, en grados, de la nave espacial respecto de la recta que une el centro de la Tierra y de la Luna, en el control titulado Angulo.
-
La velocidad adicional Δv, en m/s que en dirección tangente a la trayectoria circular proporcionan los cohetes, en el control titulado Incremento velocidad.
Se pulsa el botón titulado Lanzar
En la parte superior derecha, se proporcionan los datos del tiempo en días desde el momento del lanzamiento, la posición xR e yR de la nave espacial en fracciones del radio de la Tierra, respecto del Sistema de Referencia en rotación
En la parte inferior, se proporciona el tanto por ciento de error, de la constante J del movimiento. Cuando es mayor que la unidad, el programa se detiene.
Nota: Se ha de advertir al lector, que como el paso de integración de las ecuaciones diferenciales del movimiento es variable, la velocidad del punto que representa la partícula, no se corresponde con la velocidad real de la partícula.
Referencias
O. L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Question 11.9, pp. 348-352
Harmon N. J. Leidel C., Lindner J. F. Optimal exit: Solar escape as a restricted three-body problem. Am. J. Phys. 71(9) September 2003, pp. 871-877

