Datos del sistema Tierra-Luna:

• Masa de la Tierra, M_T=5.98·10²⁴ kg
• Radio de la Tierra, R_T=6370 km= 6.37·10⁶ m
• Masa de la Luna, M_L=7.34·10²² kg
• Radio de la Luna, R_L=1740 km= 1.74·10⁶ m
• Distancia entre la Tierra y la Luna, d=384400 km=384.4·10⁶ m

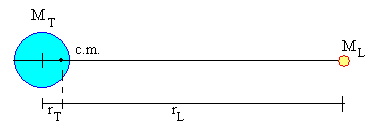
La posición del centro de masas del sistema Tierra–Luna se encuentra entre el centro de la Tierra y el centro de la Luna a una distancia r_T de la Tierra y r_L de la Luna, tal como se muestra en la figura. Como la masa de la Tierra es mayor que la masa de la Luna M_T>M_L luego, r_T<r_L. Situando el origen en el centro de masas.

${\displaystyle 0=\frac{-M_T{r}_T+M_L{r}_L}{M_T+M_L}d=r_T+r_L}$

Despejamos r_T y r_L

${\displaystyle r_T=\frac{d·M_L}{M_L+M_T}=\text{4}{\text{.656·10}}^{\text{6}}\text{m}{r}_L=\frac{d·M_T}{M_L+M_T}=379.344{\text{·10}}^{\text{6}}\text{m }}$

La posición del centro de masas del sistema Tierra-Luna está en el interior de la Tierra, más cerca de la superficie que del centro.

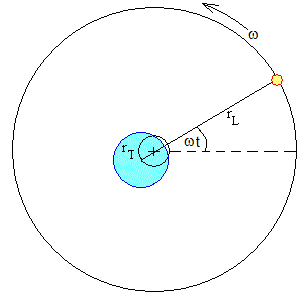
Supondremos que el centro de la Tierra y el centro de la Luna se mueven en órbitas circulares de radios r_T y r_L, respectivamente, alrededor de su centro de masas común.

El centro de la Luna describe una trayectoria circular de radio r_L bajo la acción de la fuerza de atracción de la Tierra, que dista d de su centro. Si ω es la velocidad angular constante. Aplicando la dinámica del movimiento circular uniforme a la Luna

${\displaystyle M_L{\omega }^2{r}_L=G\frac{M_T{M}_L}{d^2}}$

El centro de la Tierra describe una trayectoria circular de radio r_T bajo la acción de la fuerza de atracción de la Luna, que dista d de su centro. Si ω es la velocidad angular constante. Aplicando la dinámica del movimiento circular uniforme a la Tierra

${\displaystyle M_T{\omega }^2{r}_T=G\frac{M_T{M}_L}{d^2}}$

Despejamos la velocidad angular ω de una u otra ecuación

${\displaystyle {\omega }^2=G\frac{M_L+M_T}{d^3}\omega =2.67·{10}^{-6}\text{rad/s}}$

El periodo P=2π/ω=27.2 días

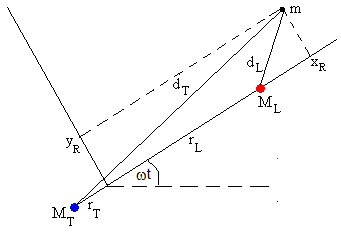
Las distancias de la partícula al centro de la Tierra y al centro de la Luna son, respectivamente

${\displaystyle \begin{array}{l}{d}_L=\sqrt{{(x_R-r_L)}^2+y_R^2}\\ d_T=\sqrt{{(x_R+r_T)}^2+y_R^2}\end{array}}$

Movimiento de una partícula bajo la influencia de la Tierra y la Luna

Sea d=r_T+r_L la distancia entre los centros de la Tierra y la Luna. Situamos un Sistema de Referencia Inercial con origen en el centro de masas del sistema Tierra-Luna. En el instante t, el ángulo que forma la recta que une el centro de la Tierra con el centro de la Luna forma un ángulo ωt, con el eje X.

La posición de la partícula en el instante t es (x, y). La posición de la Luna es (r_L·cos(ωt), r_L·sin(ωt)). La posición de la Tierra es (-r_T·cos(ωt), -r_T·sin(ωt))

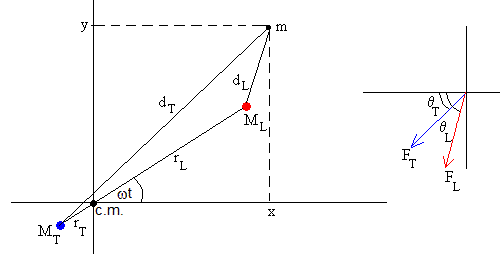
La distancia entre la Luna y la partícula y entre la Tierra y la partícula son, respectivamente

${\displaystyle \begin{array}{l}{d}_L=\sqrt{{(x-r_L\cos (\omega t))}^2+{(y-r_L\text{sin}(\omega t))}^2}\\ d_T=\sqrt{{(x+r_T\cos (\omega t))}^2+{(y+r_T\text{sin}(\omega t))}^2}\end{array}}$

Las componentes de la fuerza de atracción que ejerce la Luna y la Tierra sobre la partícula son

${\displaystyle \begin{array}{l}{F}_x=-G\frac{M_{T}m}{d_T^2}\cos {\theta }_T-G\frac{M_{L}m}{d_L^2}\cos {\theta }_L=-G\frac{M_{T}m}{d_T^2}\frac{x+r_T\cos (\omega t)}{d_T}-G\frac{M_{L}m}{d_L^2}\frac{x-r_L\cos (\omega t)}{d_T}\\ F_y=-G\frac{M_{T}m}{d_T^2}\text{sin}{\theta }_T-G\frac{M_{L}m}{d_L^2}\text{sin}{\theta }_L=-G\frac{M_{T}m}{d_T^2}\frac{y+r_T\text{sin}(\omega t)}{d_T}-G\frac{M_{L}m}{d_L^2}\frac{y-r_L\text{sin}(\omega t)}{d_T}\end{array}}$

Aplicamos la segunda ley de Newton md²x/dt²=F_x, y md²y/dt²=F_y

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-G\frac{M_T}{d_T^3}\left(x+r_T\cos (\omega t)\right)-G\frac{M_L}{d_L^3}\left(x-r_L\cos (\omega t)\right)\\ \frac{d^{2}y}{d{t}^2}=-G\frac{M_T}{d_T^3}\left(y+r_T\text{sin}(\omega t)\right)-G\frac{M_L}{d_L^3}\left(y-r_L\text{sin}(\omega t)\right)\end{array}}$

Las fuerzas se pueden derivar, alternativamente, de la energía potencial

${\displaystyle \begin{array}{l}V(x,y)=-G\frac{M_{T}m}{d_T}-G\frac{M_{L}m}{d_L}\\ \begin{array}{l}{F}_x=-\frac{\partial V}{\partial x}=-G\frac{M_{T}m}{d_T^3}\left(x+r_T\cos (\omega t)\right)-G\frac{M_{L}m}{d_L^3}\left(x-r_L\cos (\omega t)\right)\hfill \\ F_y=-\frac{\partial V}{\partial y}=-G\frac{M_{T}m}{d_T^3}\left(y+r_T\sin (\omega t)\right)-G\frac{M_{L}m}{d_L^3}\left(y-r_L\sin (\omega t)\right)\hfill \end{array}\end{array}}$

Sistema de Referencia en rotación

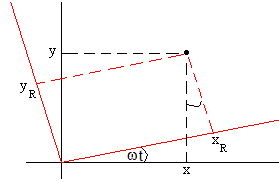
Establecemos un nuevo Sistema de Referencia No Inercial con el mismo origen que se mueve con velocidad angular ω, con respecto del Sistema de Referencia Inercial. El eje X_R del nuevo Sistema de Referencia es la recta que pasa por el centro de la Tierra y el Centro de la Luna.

En la figura, se muestra la relación entre las posición de la partícula (x, y) en el Sistema de Referencia Inercial y la posición (x_R, y_R) en el Sistema de Referencia en rotación.

x=x_R·cos(ωt)-y_R·sin(ωt)
y=x_R·sin(ωt)+y_R·cos(ωt)

Las distancias de la partícula al centro de la Tierra y al centro de la Luna son, respectivamente

${\displaystyle \begin{array}{l}{d}_L=\sqrt{{(x_R-r_L)}^2+y_R^2}\\ d_T=\sqrt{{(x_R+r_T)}^2+y_R^2}\end{array}}$

Calculamos las derivadas segundas de x e y

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\omega \left(-x_R\text{sin}(\omega t)-y_R\cos (\omega t)\right)+\frac{d{x}_R}{dt}\cos (\omega t)-\frac{d{y}_R}{dt}\text{sin}(\omega t)\\ \frac{dy}{dt}=\omega \left(x_R\cos (\omega t)-y_R\text{sin}(\omega t)\right)+\frac{d{x}_R}{dt}\text{sin}(\omega t)+\frac{d{y}_R}{dt}\cos (\omega t)\end{array}}$

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\{\begin{array}{l}-{\omega }^2\left(x_R\cos (\omega t)-y_R\text{sin}(\omega t)\right)-2\omega \left(\frac{d{x}_R}{dt}\text{sin}(\omega t)+\frac{d{y}_R}{dt}\cos (\omega t)\right)\\ +\frac{d^2{x}_R}{d{t}^2}\cos (\omega t)-\frac{d^2{y}_R}{d{t}^2}\text{sin}(\omega t)\end{array}\\ \frac{d^{2}y}{d{t}^2}=\{\begin{array}{l}-{\omega }^2\left(x_R\text{sin}(\omega t)+y_R\cos (\omega t)\right)+2\omega \left(\frac{d{x}_R}{dt}\cos (\omega t)-\frac{d{y}_R}{dt}\text{sin}(\omega t)\right)\\ +\frac{d^2{x}_R}{d{t}^2}\text{sin}(\omega t)+\frac{d^2{y}_R}{d{t}^2}\cos (\omega t)\end{array}\end{array}}$

Introduciendo estas expresiones en las dos ecuaciones diferenciales de segundo orden, e igualando los coeficientes de cos(ωt) y de sin(ωt), obtenemos el siguiente sistema de dos educaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^2{x}_R}{d{t}^2}-2\omega \frac{d{y}_R}{dt}-{\omega }^2{x}_R=-G\frac{M_T}{d_T^3}\left(x_R+r_T\right)-G\frac{M_L}{d_L^3}\left(x_R-r_L\right)\\ \frac{d^2{y}_R}{d{t}^2}+2\omega \frac{d{x}_R}{dt}-{\omega }^2{y}_R=-G\frac{M_T}{d_T^3}{y}_R-G\frac{M_L}{d_L^3}{y}_R\end{array}}$

Los dos términos en el primer miembro representan las componentes de las fuerzas de Coriolis y centrífuga por unidad de masa.

Ecuaciones del movimiento adimensionales

Establecemos un sistema de unidades tal que la distancia se mide en unidades de la distancia entre la Tierra y la Luna d=r_T+r_L y el tiempo se mide en unidades tal que un periodo P (tiempo que tarda en dar una vuelta completa la Tierra y la Luna alrededor del c.m.)

${\displaystyle \omega =\sqrt{G\frac{M_L+M_T}{d^3}},P=\frac{2\pi }{\omega }}$

Llamando

${\displaystyle X_R=\frac{x_R}{d},Y_R=\frac{y_R}{d},\tau =\omega t,\alpha =\frac{r_T}{d},1-\alpha =\frac{r_L}{d}}$

Las dos ecuaciones diferenciales se convierten en

${\displaystyle \begin{array}{l}{\omega }^{2}d\frac{d^2{X}_R}{d{\tau }^2}-2{\omega }^{2}d\frac{d{Y}_R}{d\tau }-{\omega }^{2}d·X_R=-G\frac{M_T}{d^3{\left({\left(X_R+\frac{r_T}{d}\right)}^2+Y_R^2\right)}^{3/2}}d\left(X_R+\frac{r_T}{d}\right)-G\frac{M_L}{d^3{\left({\left(X_R-\frac{r_L}{d}\right)}^2+Y_R^2\right)}^{3/2}}d\left(X_R-\frac{r_L}{d}\right)\hfill \\ {\omega }^{2}d\frac{d^2{Y}_R}{d{\tau }^2}+2{\omega }^{2}d\frac{d{X}_R}{dt}-{\omega }^{2}d·Y_R=-G\frac{M_T}{d^3{\left({\left(X_R+\frac{r_T}{d}\right)}^2+Y_R^2\right)}^{3/2}}d·Y_R-G\frac{M_L}{d^3{\left({\left(X_R-\frac{r_L}{d}\right)}^2+Y_R^2\right)}^{3/2}}d·Y_R\hfill \end{array}}$

Simplificando, teniendo en cuenta que α=M_L/(M_L+M_T) y 1-α=M_T/(M_L+M_T)

${\displaystyle \{\begin{array}{l}\frac{d^2{X}_R}{d{\tau }^2}-2\frac{d{Y}_R}{d\tau }=X_R-(1-\alpha )\frac{(X_R+\alpha )}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-\alpha \frac{(X_R-1+\alpha )}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{3/2}}\\ \frac{d^2{Y}_R}{d{\tau }^2}+2\frac{d{X}_R}{dt}=Y_R-(1-\alpha )\frac{Y_R}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-\alpha \frac{Y_R}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{3/2}}\end{array}}$

Energía potencial

El segundo miembro del sistema de dos ecuaciones diferenciales, se obtiene derivando el potencial V(X_R, Y_R) respecto de X_R y respecto de Y_R

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{d^2{X}_R}{d{\tau }^2}-2\frac{d{Y}_R}{d\tau }=-\frac{\partial V}{\partial X_R}\\ \frac{d^2{Y}_R}{d{\tau }^2}+2\frac{d{X}_R}{dt}=-\frac{\partial V}{\partial Y_R}\end{array}\\ V\left(X_R,Y_R\right)=-\frac{1}{2}(X_R^2+Y_R^2)-\frac{(1-\alpha )}{\sqrt{{\left(X_R+\alpha \right)}^2+Y_R^2}}-\frac{\alpha }{\sqrt{{\left(X_R-1+\alpha \right)}^2+Y_R^2}}\end{array}}$

• V(X_R, Y_R)→-∞ en las posiciones de los centros de la Tierra (-α, 0) y de la Luna (1-α, 0)
• V(X_R, Y_R)→-∞ cuando X_R e Y_R son grandes como consecuencia del último término, debido a la rotación.

Para el sistema Tierra-Luna el parámetro α=M_L/(M_T+M_L)=0.0121. Representamos la función V(X_R, Y_R)

${\displaystyle -\frac{(1-\alpha )}{\sqrt{{\left(X_R+\alpha \right)}^2+Y_R^2}}-\frac{\alpha }{\sqrt{{\left(X_R-1+\alpha \right)}^2+Y_R^2}}-\frac{1}{2}(X_R^2+Y_R^2)}$

MT=5.98e24; %masa de la Tierra
ML=7.349e22; %masa de la Luna
alfa=ML/(ML+MT);

[x,y] = meshgrid(-1.5:0.05:1.5);
V=-(1-alfa)./sqrt((x+alfa).^2+y.^2)-alfa./sqrt((x-1+alfa).^2+y.^2)-(x.^2+y.^2)/2;
surf(x,y,V)
zlim([-2.5,-1])
xlabel('x'); 
ylabel('y'); 
zlabel('V(x,y)')
title('Energía potencial')
view(30,45)

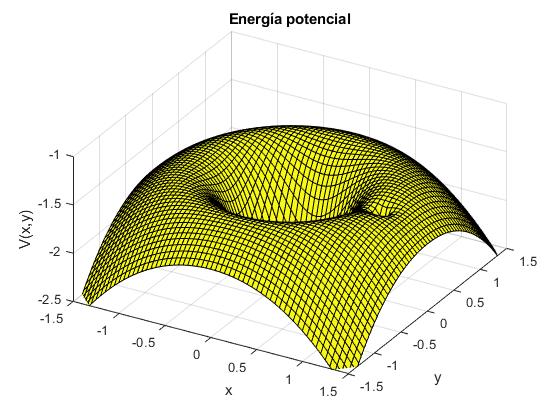
Posiciones de equilibrio

Hay cinco posiciones de equilibrio o la fuerza es nula, son los denominados puntos de Lagrange

${\displaystyle \overrightarrow{F}=-\frac{\partial V}{\partial X_R}\widehat{i}-\frac{\partial V}{\partial Y_R}\widehat{j}}$

Las dos derivadas parciales deben de ser nulas simultáneamente

${\displaystyle \begin{array}{l}\frac{\partial V}{\partial X_R}=(1-\alpha )\frac{\left(X_R+\alpha \right)}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{3/2}}+\alpha \frac{\left(X_R-1+\alpha \right)}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-X_R=0\\ \frac{\partial V}{\partial Y_R}=(1-\alpha )\frac{Y_R}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{3/2}}+\alpha \frac{Y_R}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-Y_R=0\end{array}}$

Puntos L₄ y L₅

Las dos posiciones más sencillas de encontrar son las denominadas L₄ y L₅, son simétricas respecto del eje X (dirección que une la Tierra y la Luna). Cuando Y_R≠0, dividimos la segunda ecuación por Y_R y tenemos el sistema de ecuaciones

${\displaystyle \begin{array}{l}(1-\alpha )\frac{\left(X_R+\alpha \right)}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{3/2}}+\alpha \frac{\left(X_R-1+\alpha \right)}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-X_R=0\\ (1-\alpha )\frac{1}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{3/2}}+\alpha \frac{1}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-1=0\end{array}}$

• Multiplicamos la segunda por -(X_R+α) y la sumamos a la primera

${\displaystyle \begin{array}{l}-\alpha \frac{1}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{3/2}}+\alpha =0\\ {\left(X_R-1+\alpha \right)}^2+Y_R^2=1\end{array}}$

• Multiplicamos la segunda por -(X_R-1+α) y la sumamos a la primera

${\displaystyle \begin{array}{l}\frac{1-\alpha }{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-(1-\alpha )=0\\ {\left(X_R+\alpha \right)}^2+Y_R^2=1\end{array}}$

Los dos puntos de Lagrange L₄ y L₅ son las intersecciones de las circunferencias de centros: la Tierra (0,-α) y la Luna (0, 1-α) y radio unidad. Resolviendo el sistema de dos ecuaciones con dos incógnitas obtenemos,

${\displaystyle X_R=\frac{1}{2}-\alpha ,Y_R=\pm \frac{\sqrt{3}}{2}}$

Representamos la energía potencial en las proximidades de unos de los dos puntos

MT=5.98e24; %masa de la Tierra
ML=7.349e22; %masa de la Luna
alfa=ML/(ML+MT);

%punto de Lagrange (0.8517,0)
X=0.3:0.01:0.7;
Y=0.7:0.01:1.1;
[x,y] = meshgrid(X,Y);
V=@(x,y) -(1-alfa)./sqrt((x+alfa).^2+y.^2)-alfa./sqrt((x-1+alfa).^2+y.^2)
-(x.^2+y.^2)/2;
hold on
mesh(x,y,V(x,y))
x1=1/2-alfa; y1=sqrt(3)/2; %punto de Lagrange
yy=ones(1,length(X))*y1;
plot3(X, yy,V(X,y1), 'color','r')
xx=ones(1,length(Y))*x1;
plot3(xx, Y,V(x1,Y), 'color','r')
plot3(x1,y1,V(x1,y1),'ko','markersize',4,'markeredgecolor','k',
'markerfacecolor','k')
hold off
xlabel('x'); 
ylabel('y'); 
zlabel('V(x,y)')
title('Potencial V(x,y)')
view(25,15)

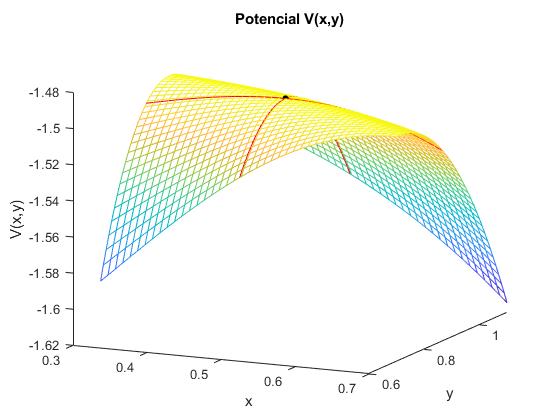
Puntos L₁, L₂ y L₃

Los otros tres puntos de Lagrange L₁, L₂ y L₃, se encuentran en el eje X, (línea que une el centro de la Tierra y de la Luna)

Representamos la energía potencial V(X_R, 0)

MT=5.98e24; %masa de la Tierra
ML=7.349e22; %masa de la Luna
alfa=ML/(ML+MT);

V=@(x,y) -(1-alfa)./sqrt((x+alfa).^2+y.^2)-alfa./
sqrt((x-1+alfa).^2+y.^2)-(x.^2+y.^2)/2;
f=@(x) V(x,0);
fplot(f,[-1.5,1.5])
grid on
ylim([-2.5,-1])
xlabel('x'); 
ylabel('V(x,0)')
title('Energía potencial, Y=0')

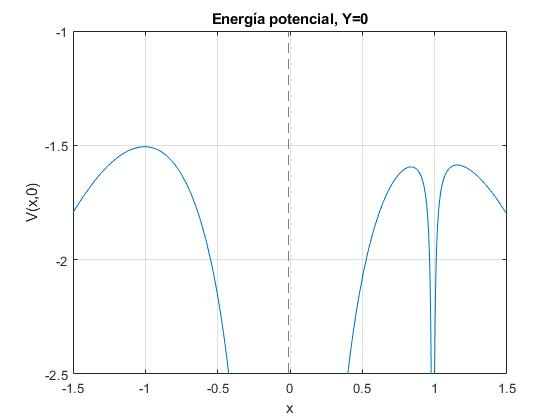
Observamos que hay tres posiciones X_R en la que V(X_R, 0) presenta un máximo

Cuando Y_R=0, se cumple que $\frac{\partial V}{\partial Y_R}=0$ y buscamos las raíces con la primera ecuación

${\displaystyle (1-\alpha )\frac{\left(X_R+\alpha \right)}{{\left|X_R+\alpha \right|}^3}+\alpha \frac{\left(X_R-1+\alpha \right)}{{\left|X_R-1+\alpha \right|}^3}-X_R=0}$

• Para X_R<-α, los dos numeradores son negativos, simplificamos

${\displaystyle -\frac{(1-\alpha )}{{\left(X_R+\alpha \right)}^2}-\frac{\alpha }{{\left(X_R-1+\alpha \right)}^2}-X_R=0}$

>> syms x k;
>> z=(1-k)*(x-1-k)^2+k*(x+k)^2+x*(x-1-k)^2*(x+k)^2;
>> zz=collect(z)
zz =x^5 - 2*x^4 + ((k + 1)^2 + k^2 - 2*k*(2*k + 2))*x^3 + (2*k*(k + 1)^2 - 
k^2*(2*k + 2) + 1)*x^2 + ((2*k + 2)*(k - 1) + k^2*(k + 1)^2 + 2*k^2)*x +
 k^3 - (k - 1)*(k + 1)^2
>> z=subs(zz,k,alfa);
>> p=sym2poly(z);
>> roots(p)
ans =
  -1.0050 + 0.0000i
   0.4917 + 0.8589i
   0.4917 - 0.8589i
   1.0108 + 0.0791i
   1.0108 - 0.0791i

Vemos que se obtiene un polinomio zz de quinto grado, cuyos coefcientes dependen del valor de k=α. Se obtienen cinco raíces mediante roots una de las cuales es real, la primera

• Para -α<X_R<1-α, (ente los centros de la Tierra y la Luna), el numerador de la izquierda es positivo y el de la derecha es negativo, simplificamos

${\displaystyle \frac{1-\alpha }{{\left(X_R+\alpha \right)}^2}-\frac{\alpha }{{\left(X_R-1+\alpha \right)}^2}-X_R=0}$

>>  z=-(1-k)*(x-1-k)^2+k*(x+k)^2+x*(x-1-k)^2*(x+k)^2;
>> zz=subs(z,k,alfa);
>> p=sym2poly(zz)
>> roots(p)
ans =
  -0.5068 + 0.8614i
  -0.5068 - 0.8614i
   1.0809 + 0.1460i
   1.0809 - 0.1460i
   0.8517 + 0.0000i

Se obtienen cinco raíces, una es real, la última

• Para X_R>1-α, el numerador de la izquierda y de la derecha son positivos, simplificamos

${\displaystyle \frac{1-\alpha }{{\left(X_R+\alpha \right)}^2}+\frac{\alpha }{{\left(X_R-1+\alpha \right)}^2}-X_R=0}$

>> z=-(1-k)*(x-1-k)^2-k*(x+k)^2+x*(x-1-k)^2*(x+k)^2;
>> zz=subs(z,k,alfa);
>> p=sym2poly(zz);
>> roots(p)
ans =
  -0.5054 + 0.8636i
  -0.5054 - 0.8636i
   1.1729 + 0.0000i
   0.9189 + 0.1315i
   0.9189 - 0.1315i

Se obtienen cinco raíces, una es real, la tercera

Juntamos todas las porciones de código en un único script

MT=5.98e24; %masa de la Tierra
ML=7.349e22; %masa de la Luna
alfa=ML/(ML+MT);

syms k x;
z=(1-k)*(x-1-k)^2+k*(x+k)^2+x*(x-1-k)^2*(x+k)^2;
zz=subs(z,k,alfa);
p=sym2poly(zz);
raices=roots(p);
for i=1:length(raices)
    if isreal(raices(i))
        disp(raices(i))
    end
end

z=-(1-k)*(x-1-k)^2+k*(x+k)^2+x*(x-1-k)^2*(x+k)^2;
zz=subs(z,k,alfa);
p=sym2poly(zz);
raices=roots(p);
for i=1:length(raices)
    if isreal(raices(i))
        disp(raices(i))
    end
end

z=-(1-k)*(x-1-k)^2-k*(x+k)^2+x*(x-1-k)^2*(x+k)^2;
zz=subs(z,k,alfa);
p=sym2poly(zz);
raices=roots(p);
for i=1:length(raices)
    if isreal(raices(i))
        disp(raices(i))
    end
end

Las tres posiciones (X_R, 0) de los puntos de Lagrange L₃, L₁ y L₂ son las siguientes

   -1.0050
    0.8517
    1.1729

Observamos más de cerca la energía potencial V(X_R, Y_R) en las proximidades de L₁

MT=5.98e24; %masa de la Tierra
ML=7.349e22; %masa de la Luna
alfa=1/(1+MT/ML);

%punto de Lagrange (0.8517,0)
X=0.8:0.005:0.9;
Y=-0.1:0.005:0.1;
[x,y] = meshgrid(X,Y);
V=@(x,y) -(1-alfa)./sqrt((x+alfa).^2+y.^2)-alfa./sqrt((x-1+alfa).^2+y.^2)
-(x.^2+y.^2)/2;
hold on
mesh(x,y,V(x,y))
x1=0.8517;
plot3(x1,0,V(x1,0),'ko','markersize',4,'markeredgecolor','k',
'markerfacecolor','k')
yy=zeros(1,length(X));
plot3(X, yy,V(X,0), 'color','r')
xx=ones(1,length(Y))*x1;
plot3(xx, Y,V(x1,Y), 'color','r')
hold off
%zlim([-2.5,-1])
xlabel('x'); 
ylabel('y'); 
zlabel('V(x,y)')
view(30,45)

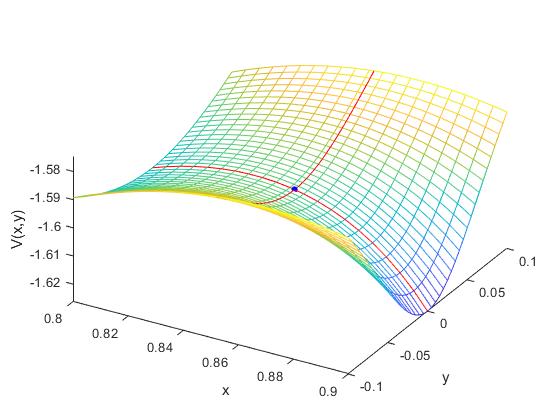
Se trata de un punto de ensilladura, es máximo a lo largo del eje X (línea que une el centro de la Tierra y de la Luna) y mínimo a lo largo de la dirección perpendicular que pasa por el punto

Estabilidad

Calculamos las derivadas segundas de V(X_R, Y_R)

${\displaystyle \begin{array}{l}\frac{{\partial }^{2}V}{\partial X_R^2}=-3\frac{(1-\alpha ){\left(X_R+\alpha \right)}^2}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{5/2}}+\frac{(1-\alpha )}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-3\frac{\alpha {\left(X_R-1+\alpha \right)}^2}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{5/2}}+\frac{\alpha }{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-1\\ \frac{{\partial }^{2}V}{\partial Y_R^2}=-3\frac{(1-\alpha )Y_R^2}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{5/2}}+\frac{(1-\alpha )}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-3\frac{\alpha Y_R^2}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{5/2}}+\frac{\alpha }{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{3/2}}-1\\ \frac{\partial }{\partial Y_R}\left(\frac{\partial V}{\partial X_R}\right)=\frac{\partial }{\partial X_R}\left(\frac{\partial V}{\partial Y_R}\right)=-3\frac{(1-\alpha )\left(X_R+\alpha \right)Y_R}{{\left({\left(X_R+\alpha \right)}^2+Y_R^2\right)}^{5/2}}-3\frac{\alpha \left(X_R-1+\alpha \right)Y_R}{{\left({\left(X_R-1+\alpha \right)}^2+Y_R^2\right)}^{5/2}}\end{array}}$

En este script, Math Symbolic de MATLAB realiza el cálculo de las derivadas segundas

MT=5.98e24; %masa de la Tierra
ML=7.349e22; %masa de la Luna
alfa=ML/(ML+MT);

%puntos de Lagrange
xL=[-1.0050, 0.8517, 1.1729, 1/2-alfa, 1/2-alfa];
yL=[0,0,0,sqrt(3)/2,-sqrt(3)/2];

syms x y k; %k es alfa
V=-(1-k)/sqrt((x+k)^2+y^2)-k/sqrt((x-1+k)^2+y^2)-(x^2+y^2)/2;
Vxx=diff(V,x,2);
Vyy=diff(V,y,2);
Vxy=diff(diff(V,x),y);
for i=1:length(xL)
    disp([double(subs(Vxx,{k,x,y},{alfa, xL(i),yL(i)})), 
double(subs(Vyy,{k,x,y},{alfa, xL(i),yL(i)})),
double(subs(Vxy,{k,x,y},{alfa, xL(i),yL(i)}))])
end

   -3.0217    0.0109         0
  -13.6834    5.3417         0
   -6.0195    1.5097         0
   -0.7500   -2.2500   -1.2675
   -0.7500   -2.2500    1.2675

Los tres primeros puntos de Lagrange L₁, L₂ y L₃ cumplen

${\displaystyle \frac{{\partial }^{2}V}{\partial X_R^2}<\mathrm{0,}\frac{{\partial }^{2}V}{\partial Y_R^2}>\mathrm{0,}\frac{{\partial }^{2}V}{\partial X_R·\partial Y_R}=0}$

Los dos restantes puntos de Lagrange L₄ y L₅ cumplen la condicción de máximo y por tanto, son inestables

${\displaystyle \frac{{\partial }^{2}V}{\partial X_R^2}<\mathrm{0,}\frac{{\partial }^{2}V}{\partial Y_R^2}<\mathrm{0,}\frac{{\partial }^{2}V}{\partial X_R·\partial Y_R}\ne 0}$

Si estuvieramos en un sistema de referencia fijo, concluiríamos que los cinco puntos de equilibrio son inestables, la fuerza $\overrightarrow{F}=-\frac{\partial V}{\partial X_R}\widehat{i}-\frac{\partial V}{\partial Y_R}\widehat{j}$, sobre una partícula de masa m estaría dirigida hacia afuera desde cada uno de dichos puntos cuando la partícula está cerca de los mismos. Sin embargo, el sistema de referencia está en rotación y en particular, para los puntos L₄ y L₅ hay que tener en cuenta la fuerza de Coriolis que como es perpendicular al vector velocidad no realiza trabajo alguno. Es posible, por tanto, que partículas describan trayectorias alrededor de estos dos puntos, siguiendo curvas de nivel (potencial constante). La energía cinética y potencial de dichas partículas se mantendría aproximadamente constantes

Puntos de Lagrange

Representamos la energía potencial V(X_R, Y_R) mediante curvas de nivel utilizando fcontour, la Tierra (punto de color azul), la Luna (de color rojo) y los cinco puntos de Lagrange (en color negro). Se muestra como los dos últimos puntos son el resultado de la intersección de dos circunferencias de radio unidad, centradas en la Tierra y la Luna, respectivamente

MT=5.98e24; %masa de la Tierra
ML=7.349e22; %masa de la Luna
alfa=ML/(ML+MT);

V=@(x,y) -(1-alfa)./sqrt((x+alfa).^2+y.^2)-alfa./sqrt((x-1+alfa).^2+y.^2)
-(x.^2+y.^2)/2;
hold on
fcontour(V,'LevelList',-1.60:0.01:-1.50)
colorbar

%Tierra y Luna
plot(-alfa,0,'bo','markersize',4,'markeredgecolor','b','markerfacecolor','b')
plot(1-alfa,0,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
%puntos de Lagrange
fplot(@(t) cos(t)-alfa,@(t) sin(t), [0,2*pi],'lineStyle','--')
fplot(@(t) cos(t)+1-alfa, @(t) sin(t), [0,2*pi],'lineStyle','--')
xL=[-1.0050, 0.8517, 1.1729, 1/2-alfa, 1/2-alfa];
yL=[0,0,0,sqrt(3)/2,-sqrt(3)/2];
for i=1:length(xL)
    plot(xL(i),yL(i),'ko','markersize',4,'markeredgecolor','k',
'markerfacecolor','k')
end

hold off
xlim([-1.5,1.5])
ylim([-1.5,1.5])
axis square
grid on
xlabel('x')
ylabel('y')
title('Puntos de Lagrange')

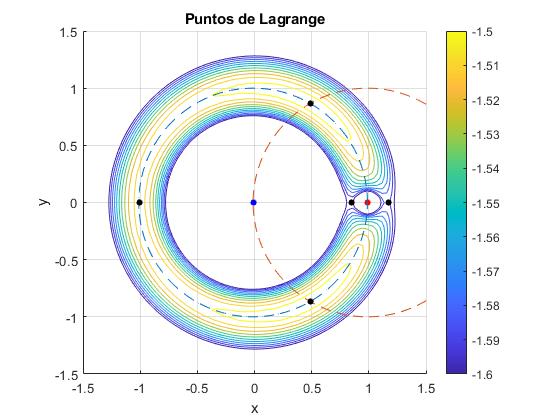
Referencias

Keith R. Symon. Mechanics. Addison-Wesley Publishing Company, Second edition, pp. 285-290

Grant R. Fowles, George L. Cassiday. Analytical Mechanics. Edt. Thomson Brooks/Cole (2005), pp. 291-295