Movimiento relativo de dos cuerpos en órbitas alrededor de la Tierra (I)
Movimiento circular de la nave espacial alrededor de la Tierra
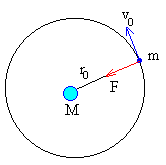
Aplicamos la ecuación de la dinámica del movimiento circular, para calcular la velocidad de la nave espacial de masa m que describe un movimiento circular de radio r0.
donde G=6.67·10-11 Nm2/kg2, y M=5.98·1024 kg es la masa de la Tierra y R=6.37·106 m es su radio.
Ejemplo
Supongamos que la nave espacial describe una órbita circular a una altura de 4000 km por encima de la superficie de la Tierra r0=6.37·106+4.0·106 =10.37·106 m
El tiempo que tarda en dar una vuelta es
P0=2πr0/v0=10506 s
Posición relativa del cuerpo respecto de la nave espacial
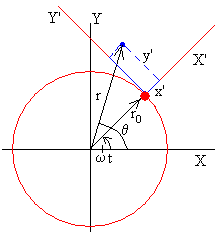
La posición del cuerpo respecto del Sistema de Referencia Inercial situado en el centro de la Tierra es
x=r·cos(θ)
y=r·sin(θ)
donde r y θ son funciones del tiempo t
La posición del cuerpo visto por un astronauta que viaja en la nave espacial o bien, respecto del Sistema de Referencia no Inercial OX’Y’ es
x’=r·cos(θ-ωt)-r0
y’=r·sin(θ-ωt)
siendo ω=v0/r0 la velocidad angular de rotación constante de la nave espacial y r0 el radio de su órbita.
En el Sistema de Referencia no Inercial el eje X' señala la dirección radial, y el eje Y' la dirección tangente a la circunferencia de radio r0. Si x'>0 el cuerpo está por encima de la nave espacial, y si x'<0 el cuerpo está por debajo. Si y'>0 el cuerpo se mueve por delante y si y'<0 el cuerpo se mueve detrás de la nave espacial.
Ecuaciones del movimiento relativo
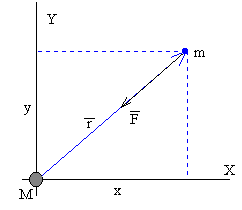
El cuerpo de masa m está sometido a una fuerza atractiva cuya dirección es radial y apuntando hacia el centro de la Tierra. El módulo de la fuerza viene dado por la ley de la Gravitación Universal
Siendo r la distancia entre el centro del cuerpo y el centro de la Tierra, y x e y su posición respecto del Sistema de Referencia Inercial cuyo origen está situado en el centro de la Tierra.
Las componentes de la fuerza son
Aplicando la segunda ley de Newton, y expresando la aceleración como derivada segunda de la posición, tenemos un sistema de dos ecuaciones diferenciales de segundo orden.
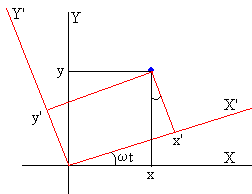
Vamos a describir el movimiento desde el punto de vista de un Sistema de Referencia no Inercial que gira respecto del Sistema de Referencia Inercial con velocidad angular ω=v0/r0 (la velocidad angular constante de la nave espacial).
Las relaciones entre las coordenadas del cuerpo medidas en el Sistema de Referencia Inercial (x, y) y las medidas en el Sistema de Referencia no Inercial (x’, y’) son
x=x’cos(ωt)-y’sin(ωt)
y=x’sin(ωt)+y’cos(ωt)
Calculamos las derivadas segundas de x y de y respecto del tiempo t, d2x/dt2 y d2y/dt2.
Multiplicamos la primera ecuación por cos(ωt) y la segunda por sin(ωt) y las sumamos. Obtenemos la ecuación diferencial
Multiplicamos la primera ecuación por -sin(ωt) y la segunda por cos(ωt) y las sumamos. Obtenemos la ecuación diferencial
Los dos términos que aparecen en la parte derecha de las dos ecuaciones diferenciales representan las pseudofuerzas por unidad de masa, denominadas de Coriolis y centrífuga.
Hemos obtenido un sistema de dos ecuaciones diferenciales en términos de x’ e y’ y de sus derivadas.
Dadas las condiciones iniciales (posición y velocidad inicial), el sistema de dos ecuaciones diferenciales se puede integrar aplicando procedimientos numéricos.
-
Movimiento del cuerpo que está a una cierta altura por encima o por debajo de la nave espacial
-
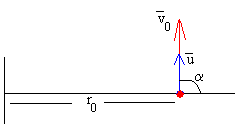
Movimiento de un cuerpo que se lanza desde la nave espacial con velocidad relativa u, haciendo un ángulo α con la dirección radial
Las condiciones iniciales son x’0=r0±h, y’0=0, (dx’/dt)0=0, (dy’/dt)0=0.
Siendo r0, el radio de la órbita de la nave espacial, h es la altura por encima o por debajo de un cuerpo inicialmente sujeto a la nave. El objeto está inicialmente en reposo en el S. R. no inercial, respecto de la nave espacial
Las condiciones iniciales son x’0=r0, y’0=0, (dx’/dt)0=u·cosα, (dy’/dt)0= u·sinα
Como la nave espacial dista r0 del centro de la Tierra, la posición del cuerpo vista por un astronauta que viaja en la nave espacial tiene por abscisa x’-r0 y por ordenada y’, véase la figura al principio de este apartado
Movimiento del cuerpo que está a una cierta altura sobre la nave espacial
Consideremos primero, el caso más simple, el movimiento de un cuerpo que está a una distancia h de la nave espacial medida a lo largo de la dirección radial y que en el instante inicial, tiene su misma velocidad. Se suelta el cuerpo y comprobamos que ambos se mueven en órbitas distintas.
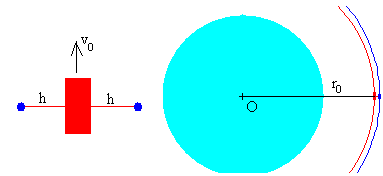
Vamos a considerar dos casos: que h sea positiva, la altura del cuerpo sea mayor que el de la nave espacial, y que h sea negativa, la altura del cuerpo sea menor que la de la nave espacial.
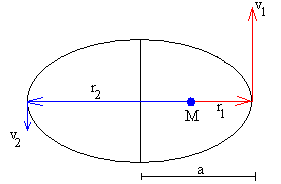
La constancia del momento angular y de la energía del cuerpo nos permiten calcular la distancia máxima o mínima r2 y su velocidad v2, conocidas la distancia mínima o máxima r1=r0+h y su velocidad v1=v0.
Despejamos v2 y r2
El semieje mayor de la elipse es a=(r1+r2)/2 y el periodo P, o tiempo que tarda el cuerpo en dar una vuelta completa es
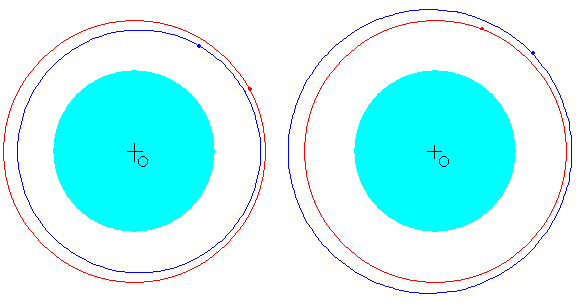
En la figura, vemos la trayectoria seguida por un cuerpo sujeto a la nave espacial y que se suelta en el instante inicial con la misma velocidad v0 que lleva la nave. En la figura de la izquierda, la altura del objeto es menor que el de la nave espacial, h<0, el cuerpo va por delante de la nave. En la figura de la derecha, la altura del objeto es mayor que el de la nave espacial, h>0, el cuerpo va por detrás de la nave.
Ejemplo
-
El cuerpo está por encima de la nave espacial
La nave espacial describe una órbita circular de 4000 km de altura, r0=6.37·106+4.0·106=10.37·106 m, del centro de la Tierra y sea h=80·103 (el cuerpo está 80 km por encima de la nave espacial)
La velocidad de la nave espacial como hemos calculado en el apartado anterior es de v0=6202 m/s y el tiempo que tarda en dar una vuelta es P0=2πr0/v0=10506 s
Dado r1=r0+h=10.37·106+80·103=10.45·106 m, y v1=6202 m/s calculamos v2 y r2
El semieje mayor de la elipse vale a=(10.45·106 +10.61·106)/2=10.53·106 m, y el periodo
Como el semieje es mayor que el radio de la órbita circular a>r0, el periodo P del movimiento del cuerpo es mayor que el de la nave espacial P0. El cuerpo va por detrás de la nave espacial
Representamos la trayectoria del cuerpo relativa a la nave espacial durante tres periodos o tres vueltas completas de la nave espacial
r=6.37e6+4000e3; %nave espacial
GM=6.67e-11*5.98e24;
w=sqrt(GM/r^3);
fg=@(t,x)[x(2);-GM*x(1)/(x(1)*x(1)+x(3)*x(3))^(3/2)+2*w*x(4)+w^2*x(1);
x(4);-GM*x(3)/(x(1)*x(1)+x(3)*x(3))^(3/2)-2*w*x(2)+w^2*x(3)];
h=80*1000; %altura
x0=[r+h, 0, 0, 0];
[t,x]=ode45(fg,[0,6*pi/w],x0);
plot(x(:,3),x(:,1)-r) %trayectoria
axis equal
grid on
xlabel('Y')
ylabel('X')
title('Abajo')
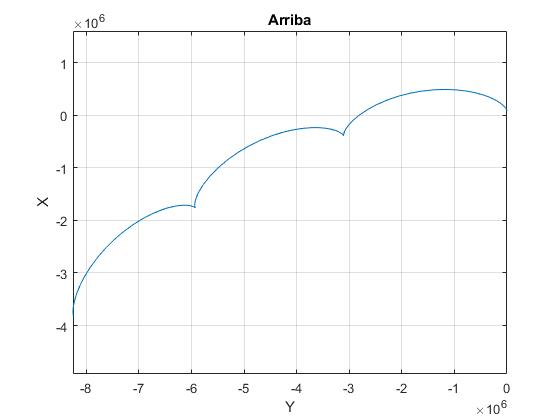
El cuerpo está por debajo de la nave espacial
Dado r1=r0-h=r1=r0+h=10.37·106-80·103=10.29·106 m, y v1=6202 m/s calculamos v2 y r2
El semieje mayor de la elipse vale a=(10.29·106 +10.13·106)/2=10.21·106 m, y el periodo P=10266 s que es menor que el periodo P0 de la nave espacial. El cuerpo va por delante de la nave espacial.
Cambiamos el signo de la altura h, el objeto está ahora por debajo de la nave espacial. Representamos la trayectoria del cuerpo relativa a la nave espacial durante tres periodos o tres vueltas completas de la nave espacial
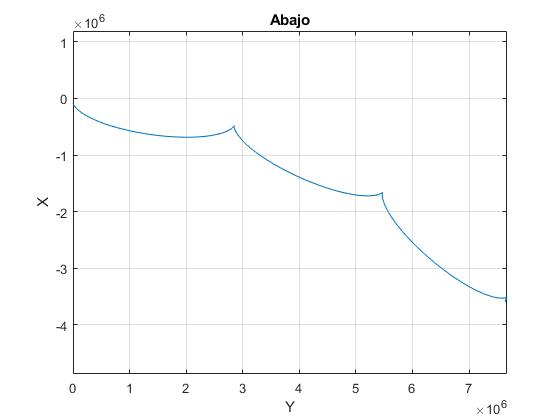
Actividades
Se introduce
-
La altura en km de la nave espacial sobre la superficie de la Tierra, en el control titulado Altura
-
La distancia h en km, medida a lo largo de la dirección radial entre la nave espacial y el cuerpo en el instante inicial, en el control titulado Distancia.
Se pulsa el botón titulado Nuevo
En la parte izquierda, se representa el movimiento de los dos cuerpos alrededor de la Tierra:
-
La nave espacial, es un punto de color rojo en órbita circular alrededor de la Tierra
-
El cuerpo, es un punto de color azul que describe una trayectoria elíptica
A la derecha, se representa la trayectoria seguida por el cuerpo vista por un astronauta que viaja en la nave espacial.
-
El eje vertical X' es la dirección radial y nos indica si el cuerpo está por encima o por debajo de la nave espacial.
-
El eje horizontal Y' es la dirección tangencial a la órbita de la nave espacial y nos indica si el cuerpo está por delante o por detrás de la nave espacial.
Las distancias tanto en el eje horizontal Y' como en el vertical X' están expresadas en km.
Para ver adecuadamente la trayectoria, se puede elegir la escala en el control titulado Escala y a continuación, se pulsa el botón titulado Nuevo.
Movimiento de un cuerpo que se lanza desde la nave espacial
Supongamos que un cuerpo de pequeña masa se lanza desde una nave espacial con velocidad relativa u y haciendo un ángulo α respecto del eje X' (dirección radial).
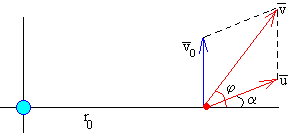
La velocidad v del cuerpo y su dirección φ respecto al Sistema Inercial de Referencia situado en el centro de la Tierra, se calculan sumando los vectores de la figura. Sus componentes son:
vx=u·cosα
vy=v0+u·sinα
El módulo de la velocidad resultante v y su dirección φ son:
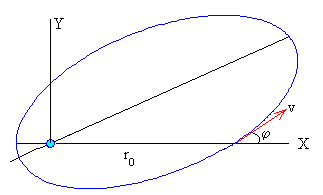
La ecuación de la trayectoria del cuerpo de masa m está determinada por la energía y el momento angular
La trayectoria es independiente de la masa m del cuerpo y es una elipse si E<0, cuyo semieje mayor está girado un cierto ángulo que se calcula poniendo r=r0 en la ecuación de la trayectoria y despejando el ángulo θ.
Ejemplo:
Sea r0=6.37·106+4.0·106, (4000 km de altura sobre la superficie de la Tierra)
-
Se lanza el cuerpo en dirección radial
La velocidad de la nave espacial como hemos calculado en el primer apartado es de v0=6202 m/s y el tiempo que tarda en dar una vuelta es P0=2πr0/v0=10506 s
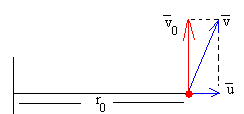
Si lanzamos el cuerpo con una velocidad u=100 m/s con α=0º.
La velocidad v del cuerpo respecto de la Tierra es
vx= 100
vy=6202
La energía
El semieje mayor de la elipse se puede calcular también mediante la fórmula
El periodo P es
El periodo es un poco mayor que el de la nave espacial
Representamos la trayectoria del objeto que es lanzado desde una nave espacial, que describe una órbita circular de 4000 km de radio, con velocidad relativa u=100 m/s en la dirección radial, α=0
r=6.37e6+4000e3; %nave espacial
GM=6.67e-11*5.98e24;
w=sqrt(GM/r^3);
fg=@(t,x)[x(2);-GM*x(1)/(x(1)*x(1)+x(3)*x(3))^(3/2)+2*w*x(4)+w^2*x(1);
x(4);-GM*x(3)/(x(1)*x(1)+x(3)*x(3))^(3/2)-2*w*x(2)+w^2*x(3)];
u=100; %velocidad de lanzamiento
alfa=0; %dirección radial
x0=[r, u*cos(alfa), 0, u*sin(alfa)];
[t,x]=ode45(fg,[0,2*pi/w],x0);
plot(x(:,3),x(:,1)-r) %trayectoria
axis equal
grid on
xlabel('Y')
ylabel('X')
title('Dirección radial')
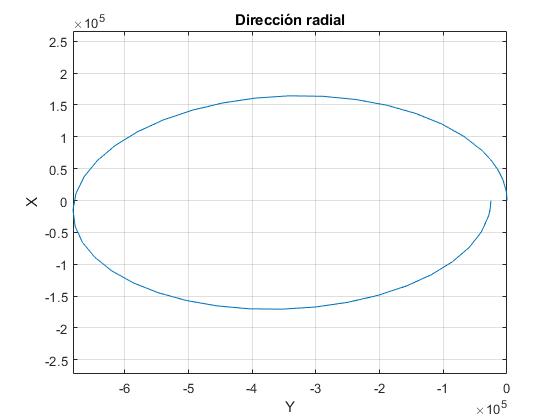
El objeto describe una trayectoria casi elíptica desde el punto de vista del astronauta. Se aleja por detrás de la nave y asciende, luego, desciende y se acerca hasta casi el lugar de partida, al cabo de un periodo de revolución de la nave espacial.
Si lanzamos el cuerpo con una velocidad u=100 m/s haciendo un ángulo de α=90º con el eje X' (dirección radial), en la dirección del movimiento de la nave espacial Y', la velocidad v del cuerpo respecto de la Tierra es
vx=0
vy=6302
La energía E=-18.61·106·m J. El semieje mayor de la elipse a=10.72·106 m y el periodo P=11040 s un poco mayor que el de la nave espacial
Representamos la trayectoria del objeto que es lanzado desde una nave espacial, que describe una órbita circular de 4000 km de radio, con velocidad relativa u=100 m/s en la dirección tangencial, α=90°
En el script anterior cambiamos el ángulo alfa de 0 a π/2 (90°). Representamos la trayectoria del objeto visto desde la nave durante dos periodos o el tiempo que tarda la nave espacial en dar dos vueltas completas
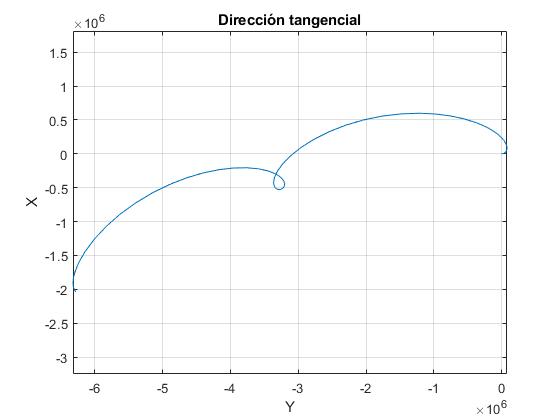
El objeto visto por un astronauta que viaja en la nave espacial, avanza al principio en la dirección del movimiento de la nave espacial, gira hacia arriba y comienza a alejarse por detrás de la nave a lo largo de la dirección tangencial Y', describiendo una trayectoria compleja. En el programa interactivo, observaremos los primeros instantes del movimiento del cuerpo vistos por el astronauta y en la imagen anterior, durante dos periodos.
Actividades
Se introduce
-
La altura en km de la nave espacial respecto de la superficie de la Tierra, en el control titulado Altura
-
La velocidad u del cuerpo que es lanzado desde la nave espacial, en el control titulado Velocidad
-
La dirección α de dicha velocidad, en el control titulado Ángulo
-
El ángulo α=0, corresponde a un lanzamiento hacia arriba (en la dirección radial),
-
α=90º, el lanzamiento es hacia delante, en la misma dirección (tangencial) y sentido que la velocidad de la nave.
-
α=180º, corresponde a un lanzamiento hacia abajo, en dirección hacia el centro de la Tierra
-
α=270º, el lanzamiento hacia atrás, en la misma dirección (tangencial) y en sentido contrario a la velocidad de la nave
Se pulsa el botón titulado Nuevo
En la parte izquierda, se representa el movimiento de los dos cuerpos alrededor de la Tierra:
-
La nave espacial es un punto de color rojo en órbita circular alrededor de la Tierra
-
El cuerpo es un punto de color azul que describe una trayectoria elíptica
A la derecha, se representa la trayectoria seguida por el cuerpo vista por un astronauta que viaja en la nave espacial.
-
El eje vertical X' es la dirección radial y nos indica si el cuerpo está por encima o por debajo de la nave espacial.
-
El eje horizontal es la dirección tangencial a la órbita de la nave espacial y nos indica si el cuerpo está por delante o por detrás de la nave espacial.
Las distancias tanto en el eje horizontal Y' como en el vertical X' están expresadas en km.
Para ver adecuadamente la trayectoria, se puede elegir la escala en el control de selección titulado Escala, y a continuación se pulsa el botón titulado Nuevo.

