Movimiento de caída de un satélite artificial debido al rozamiento con la atmósfera.

La atmósfera está formada por varias capas, definidas de acuerdo con la variación vertical de la temperatura:

la troposfera, la temperatura desciende con la altura a razón de 0.6ºC cada 100 m.
la estratosfera, la temperatura permanece prácticamente constante
la mesosfera, la temperatura aumenta y luego disminuye
la termosfera, la temperatura crece regularmente con la altura.

También se suele subdividir la atmósfera en capas de acuerdo a la composición química:

la homosfera (hasta 100 km), los constituyentes principales del aire (oxígeno y nitrógeno) permanecen en proporción constante.
la heterosfera (de 100 km a 1000 km), predominan los gases ligeros, hidrógeno, nitrógeno, helio.
la exosfera, (a partir de 1000 km) las moléculas más ligeras escapan hacia el espacio exterior venciendo la fuerza de atracción de la Tierra.

La fuerza de rozamiento sobre el satélite dependerá en general, de su forma, de la densidad del aire y de la velocidad del satélite, por lo que la ecuación del movimiento resultará bastante complicada. En esta página, haremos algunas aproximaciones que nos permitirán describir de forma sencilla el movimiento del satélite.

Órbita circular

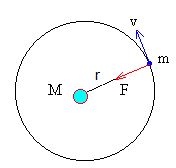
Consideremos un satélite artificial que describe una órbita circular alrededor de la Tierra de radio r. Aplicando la ecuación de la dinámica del movimiento circular uniforme tenemos que:

$G \frac{M m}{r^{2}} = m \frac{v^{2}}{r}, v = \sqrt{\frac{G M}{r}}$

donde G=6.67·10^-11 Nm²/kg², y M=5.98·10²⁴ kg es la masa de la Tierra y su radio es de 6370 km.

Como vemos en la figura, cuando el satélite describe una órbita circular, la velocidad es perpendicular a la dirección radial o a la dirección de la fuerza de atracción.

Por ser la fuerza de atracción conservativa, la energía del satélite artificial es constante en todos los puntos de la circunferencia que describe.

$E = \frac{1}{2} m v^{2} + (- G \frac{M m}{r}) = - \frac{1}{2} \frac{G M m}{r}$

La energía total E es la mitad de la energía potencial y es negativa.

Fuerza de rozamiento constante

Cuando el satélite artificial cae hacia la Tierra describe una espiral. El ángulo que forma la velocidad con la dirección radial ya no es 90º sino un ángulo 90º-φ un poco más pequeño. En otras palabras, la dirección de la velocidad está ligeramente por debajo de la dirección horizontal local. La dirección normal (perpendicular a la dirección de la velocidad) ya no coincide con la dirección radial sino que forman un ángulo φ.

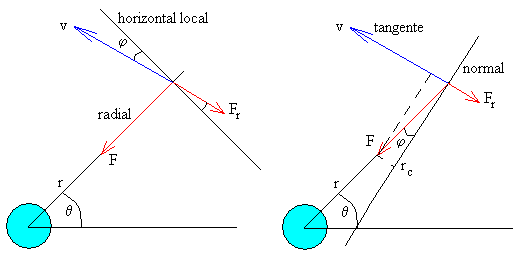
En la figura, se muestran las fuerzas sobre el satélite cuando está a una distancia r del centro de la Tierra.

La fuerza de atracción F
La fuerza de rozamiento F_r que supondremos constante y de sentido opuesto a la velocidad.

Descomponemos la fuerza F en la dirección de la velocidad (tangencial), y en la dirección perpendicular a la velocidad (normal).

Las ecuaciones del movimiento en la dirección tangencial y en la dirección normal son:

ma_t=F·sinφ-F_rma_n=F·cosφ

la primera nos da cuenta como cambia el módulo de la velocidad v del satélite con el tiempo.
la segunda, cómo cambia la dirección de la velocidad

$\begin{array}{l} m \frac{d v}{d t} = F \cdot sin φ - F_{r} \\ m \frac{v^{2}}{r_{c}} = F \cos φ \end{array}$

Donde r_c es el radio de curvatura de la trayectoria, un valor distinto al radio r de la trayectoria circular con centro en la Tierra.

Solución numérica

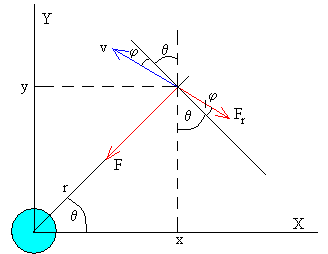
Planteamos las ecuaciones del movimiento en coordenadas rectangulares:

ma_x=-F·cosθ+F_r·sin(θ+φ)
ma_y=-F·sinθ-F_r·cos(θ+φ)

con

x=r·cosθ y=r·sinθ
v_x=-v·sin(θ+φ) v_y=v·cos(θ+φ)

Las dos ecuaciones del movimiento se transforman en un sistema de dos ecuaciones diferenciales de segundo orden, que se resuelven por procedimientos numéricos, con las condiciones iniciales t=0, x=R, y=0, v_x=0, v_y=v₀. Donde v₀ es la velocidad del satélite artificial cuando describe una órbita circular inicial de radio R.

Aproximaciones

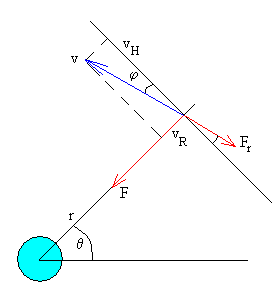
Haciendo algunas aproximaciones, la ecuación del movimiento del satélite artificial se hace más simple.

Si suponemos que el ángulo φ es pequeño y que por tanto, la componente de la velocidad v a lo largo de horizontal local es v_H=v·cosφ≈v, y que la componente radial v_R es pequeña, por lo que

sinφ≈tanφ=-v_R/v_H

La ecuación

$m \frac{v_{H}^{2}}{r} = F = G \frac{M m}{r^{2}}$

sería la de un satélite que estuviese describiendo una órbita circular de radio r con velocidad v_H=v·cosφ

Simplificando m y r y a continuación, derivando con respecto a r tenemos que

$2 v_{H} \frac{d v_{H}}{d r} = - G \frac{M}{r^{2}} = - \frac{F}{m}$

La aceleración tangencial vale

$a_{t} = \frac{d v}{d t} = \frac{d r}{d t} \frac{d v}{d r} = v_{R} \frac{d v}{d r} \approx v_{R} \frac{d v_{H}}{d r}$

De estas dos últimas ecuaciones llegamos a

$a_{t} \approx - \frac{1}{2} \frac{F}{m} \frac{v_{R}}{v_{H}} \approx \frac{1}{2} \frac{F}{m} sin φ$

Con esta aproximación, la ecuación del movimiento en la dirección tangencial

ma_t=F·sinφ-F_r

se escribe

$\frac{1}{2} F sin φ = F sin φ - F_{r}$

El ángulo que forma el vector velocidad con la horizontal local es

$sin φ = \frac{2 F_{r}}{F} = \frac{2 r^{2}}{G M} \frac{F_{r}}{m}$

Llegamos a la siguiente conclusión paradójica

ma_t=F_r

La fuerza de rozamiento incrementa el módulo v de la velocidad del satélite. En realidad, es la resultante de las dos fuerzas (atracción y rozamiento) la que tiene una componente en la dirección de la velocidad del satélite, como puede fácilmente comprobarse a partir de los esquemas de esta página.

Las ecuaciones que nos permiten obtener la posición del móvil en coordenadas polares (r, θ) en función del tiempo t son:

$\begin{array}{l} m \frac{d v}{d t} = F_{r}, v = v_{0} + \frac{F_{r}}{m} t \\ m \frac{v^{2}}{r} = G \frac{M m}{r}, r = \frac{G M}{v^{2}} \\ r \frac{d θ}{d t} = v, θ = \frac{v}{r} t \end{array}$

Donde v₀ es la velocidad del satélite artificial en la órbita circular inicial de radio R, que describe en el instante inicial t=0.

La energía inicial del satélite artificial la hemos calculado en el apartado anterior. La energía final, suponiendo de nuevo que el satélite artificial describe una órbita casi circular de radio r con velocidad v, será

$E_{f} = \frac{1}{2} m v^{2} + (- \frac{G M m}{r}) = - \frac{1}{2} \frac{G M m}{r}$

La energía perdida a causa del rozamiento del satélite artificial con la atmósfera es la diferencia

$Δ E = E_{f} - E_{i} = \frac{G M m}{2} (\frac{1}{R} - \frac{1}{r}) < 0$

Actividades

El objetivo del programa interactivo no es el de realizar un cálculo de la posición y de la velocidad del satélite artificial, sino la de mostrar su trayectoria en forma de espiral, como aumenta su velocidad a medida que desciende.

Se introduce

La altura del satélite en km, por encima de la superficie de la Tierra en el control titulado Altura.
El cociente F_r/m de la fuerza de rozamiento F_r a la masa m del satélite en el control titulado Rozamiento.

Se pulsa el botón titulado Nuevo.

Se observa el movimiento del satélite alrededor de la Tierra, hasta que choca con su superficie, una circunferencia de color azul representa la órbita circular inicial.

Se proporcionan los datos del tiempo en horas, la velocidad en m/s y la altura en km sobre la superficie de la Tierra.

A la izquierda, se representa mediante barras de colores los cambios energéticos:

en color azul, la energía cinética que es positiva
en color rojo, la energía potencial que es negativa
una raya de color claro, indica la energía total E, por unidad de masa m, cuyo valor se muestra en millones de J/kg.
Una barra de color negro señala diferencia entre la energía inicial y la final, o la pérdida de energía debido al rozamiento a medida que cae el satélite hacia la superficie de la Tierra.

Ejemplo:

Introducimos los datos

Altura h=5000 km
Rozamiento F_r/m=0.025

Calculamos el ángulo que forma la dirección de la velocidad con la horizontal local

$sin φ = \frac{2 {(6370 + 5000)}^{2} 10^{6}}{6.67 \cdot 10^{- 11} \cdot 5.98 \cdot 10^{24}} \cdot 0.025 = 0.016$

El ángulo φ es muy pequeño y va disminuyendo a medida que el satélite artificial se acerca a la Tierra.

Altura
Rozamiento

Fuerza de rozamiento proporcional al cuadrado de la velocidad

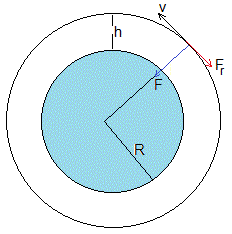
Sobre el satélite actúan dos fuerzas:

La fuerza F de atracción de la Tierra, en la dirección radial, que hace que el satélite describa una órbita circular a una altura h

$v = \sqrt{\frac{G M}{R + h}}$

A una altitud de 280 km, la velocidad es de 7.74 km/s y su periodo es de 90.08 minutos, completando 16 órbitas en un día.

La fuerza de rozamiento F_r, proporcional al cuadrado de la velocidad, en la dirección tangencial, opuesta a la velocidad

$F_{r} = C_{D} \frac{1}{2} ρ (r) A v^{2}$

Donde C_D se denomina coeficiente de arrastre, ρ es la densidad del fluido, A es el área de la sección transversal a la dirección del movimiento y v es la velocidad relativa del objeto respecto del fluido.

Un modelo simple de atmósfera es la isoterma, en la que la densidad disminuye exponencialmente con la altura

$ρ (h) = ρ_{0} \exp (- \frac{h - h_{0}}{H})$

donde ρ₀ es la densidad a la altura h₀

En este modelo válido hasta una altura de 500 km, la densidad de la atmósfera es ρ₀=6·10^-10 kg/m³ a la altura h₀=175 km, la constante H=29.5 km

A medida que el satélite cae, la densidad del aire se incrementa, aumentando la fuerza de rozamiento y por tanto, disminuyendo aún más la altura del satélite

Variación de la altura con el tiempo

Transcurren muchas horas para que la altura del satélite disminuya significativamente. El tiempo que tarda en describir una órbita es de alrededor de 90 min. Podemos suponer que el satélite describe órbitas aproximadamente circulares de radio cada vez más pequeño

La energía del satélite de masa m en una órbita de radio r es

$E = \frac{1}{2} m v^{2} + (- G \frac{M m}{r}) = - \frac{1}{2} \frac{G M m}{r}$

La disminución de la energía del satélite en el intervalo t a t+dt se debe al trabajo de la fuerza de rozamiento F_r

$\begin{array}{l} d E = {\vec{F}}_{r} \cdot \vec{v} = - (C_{D} \frac{1}{2} ρ (r) A v^{2}) v \\ \frac{1}{2} \frac{G M m}{r^{2}} \frac{d r}{d t} = - \frac{1}{2} C_{D} A ρ (r) A {(\sqrt{\frac{G M}{r}})}^{3} \\ \frac{d r}{d t} = - \frac{C_{D} A}{m} ρ (r) \sqrt{r} \end{array}$

Para un satélite situado a una altura h, r=R+h, siendo R=6378 km el radio de la Tierra

$\begin{array}{l} \frac{d h}{d t} = - \frac{C_{D} A}{m} ρ_{0} \exp (- \frac{h - h_{0}}{H}) \sqrt{R + h} \\ \frac{d h}{d t} = - k \exp (- \frac{h - 175}{29.5}) \sqrt{R + h} \end{array}$

Para un satélite artificial de masa m=8506 kg y área efectiva C_DA=41.8 m², la constante de proporcionalidad, k

$k = \frac{41.8}{8506} 6 \cdot 10^{- 10}$

Estableceremos un sistema de unidades en el que las alturas h se miden en km y el tiempo en horas.

$k = \frac{3600}{\sqrt{1000}} \frac{41.8}{8506} 6 \cdot 10^{- 10} = 0.0067 \frac{{km}^{1/2}}{h}$

Se resuelve la ecuación diferencial por procedimientos numéricos, con la siguiente condición inicial, en el instante t=0, la altura del satélite es h=280 km

k=(360/sqrt(10))*6e-10*sqrt(6.67e-11*5.98e24)*41.8/8506;
f=@(t,x) -k*sqrt(6378+x)*exp(-(x-175)/29.5); 
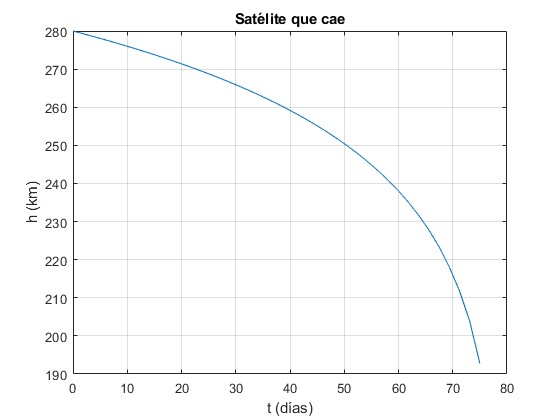
[t,x]=ode45(f,[0,75*24],280); %75 días
plot(t/24,x)
grid on
xlabel('t (días)')
ylabel('h (km)');
title('Satélite que cae')

Referencias

Mills B. D.. Satellite paradox. Am. J. Phys. 27 (1959) pp. 115-117

Arons. A. A F=ma analysis of the spinning skater and decaying satellite orbit. The Physics Teacher 37, March 1999, pp. 154-160

Miguel Fiolhais, Luis Gonzalez-Urbina, Tomasz Milewski, Carlos Chaparro, Andrea Ferroglia. Orbital Decay in the Classroom. The Physics Teacher, Vol. 61, March 2023, pp. 182-185