La fuerza que describe el movimiento de una vela solar plana, perpendicular a la dirección radial es

${\displaystyle \overrightarrow{F}=-(1-\lambda )\frac{GM}{r^2}\widehat{r}}$

Donde λ es un parámetro (lightness number) que depende de la vela y de la radiación solar

Supongamos que manejamos la vela solar de modo que el parámetro λ no es constante sino que depende del ángulo θ, de modo que λ varía entre dos límites

En la página titulada Ecuación de la trayectoria, obtuvimos la ecuación de la trayectoria a partir dela segunda ley de Newton, expresando la aceleración en coordenadas polares, llegando a la siguiente ecuación diferencial

${\displaystyle \frac{d^{2}u}{d{\theta }^2}+u=\frac{GM{m}^2}{L^2},u=\frac{1}{r}}$

Sustituimos GM por la expresión (1-λ(θ))GM

${\displaystyle \frac{d^{2}u}{d{\theta }^2}+u=\left(1-\lambda (\theta )\right)\frac{GM{m}^2}{L^2}}$

La solución de la ecuación homogénea es conocida u=Asinθ+Bcosθ

Calculamos la solución particular mediante el procedimiento de Variación de parámetros.

Buscamos una solución particular de la forma

${\displaystyle u_p(\theta )=c_1{u}_1+c_2{u}_2\{\begin{array}{l}{u}_1=\sin \theta \\ u_2=\cos \theta \end{array}}$

Donde c₁ y c₂ son funciones de θ

Derivamos con respecto de θ

${\displaystyle \frac{d{u}_p}{d\theta }=\frac{d{c}_1}{d\theta }{u}_1+c_1\frac{d{u}_1}{d\theta }+\frac{d{c}_2}{d\theta }{u}_2+c_2\frac{d{u}_2}{d\theta }}$

Tenemos cuatro términos que reducimos a dos, imponiendo la condición de que

${\displaystyle \frac{d{c}_1}{d\theta }{u}_1+\frac{d{c}_2}{d\theta }{u}_2=0}$

Calculamos la derivada segunda con respecto de θ

${\displaystyle \begin{array}{l}\frac{d{u}_p}{d\theta }=c_1\frac{d{u}_1}{d\theta }+c_2\frac{d{u}_2}{d\theta }\hfill \\ \frac{d^2{u}_p}{d{\theta }^2}=c_1\frac{d^2{u}_1}{d{\theta }^2}+c_2\frac{d^2{u}_2}{d{\theta }^2}+\frac{d{c}_1}{d\theta }\frac{d{u}_1}{d\theta }+\frac{d{c}_2}{d\theta }\frac{d{u}_2}{d\theta }\hfill \end{array}}$

Introducimos la solución particular u_p(θ) y sus derivadas en la ecuación diferencial

${\displaystyle c_1\frac{d^2{u}_1}{d{\theta }^2}+c_2\frac{d^2{u}_2}{d{\theta }^2}+\frac{d{c}_1}{d\theta }\frac{d{u}_1}{d\theta }+\frac{d{c}_2}{d\theta }\frac{d{u}_2}{d\theta }+c_1{u}_1+c_2{u}_2=\left(1-\lambda (\theta )\right)\frac{GM{m}^2}{L^2}}$

Como u₁(θ) y u₂(θ) son soluciones de la ecuación diferencial homogénea, esta expresión se reduce a

${\displaystyle c\frac{d{c}_1}{d\theta }\frac{d{u}_1}{d\theta }+\frac{d{c}_2}{d\theta }\frac{d{u}_2}{d\theta }=\left(1-\lambda (\theta )\right)\frac{GM{m}^2}{L^2}}$

Que junto a la condición impuesta al principio, forman un sistema de dos ecuaciones diferenciales de primer orden

${\displaystyle \{\begin{array}{l}\frac{d{c}_1}{d\theta }\sin \theta +\frac{d{c}_2}{d\theta }\cos \theta =0\\ \frac{d{c}_1}{d\theta }\cos \theta -\frac{d{c}_2}{d\theta }\sin \theta =\left(1-\lambda (\theta )\right)\frac{GM{m}^2}{L^2}\end{array}}$

Multiplicamos la primera por sinθ y la segunda por cosθ y sumamos

${\displaystyle \begin{array}{l}\frac{d{c}_1}{d\theta }=\left(1-\lambda (\theta )\right)\frac{GM{m}^2}{L^2}\cos \theta \\ c_1=\frac{GM{m}^2}{L^2}{\displaystyle \int \left(1-\lambda (\theta )\right)\cos \theta ·d\theta }\end{array}}$

Ya que buscamos la solución particular, aquí no precisamos de la constante de integración

Utilizamos la primera ecuación para calcular c₂(θ)

${\displaystyle \begin{array}{l}\frac{d{c}_2}{d\theta }=-\left(1-\lambda (\theta )\right)\frac{GM{m}^2}{L^2}\sin \theta \\ c_2=-\frac{GM{m}^2}{L^2}{\displaystyle \int \left(1-\lambda (\theta )\right)\sin \theta ·d\theta }\end{array}}$

La solución completa de la ecuación diferencial es

${\displaystyle u=\frac{GM{m}^2}{L^2}\left\{\sin \theta {\displaystyle \int \left(1-\lambda (\theta )\right)\cos \theta ·d\theta }-\cos \theta {\displaystyle \int \left(1-\lambda (\theta )\right)\sin \theta ·d\theta }\right\}+A\sin \theta +B\cos \theta }$

Donde A y B se determinan a partir de las condiciones iniciales.

Ejemplo

Supongamos que λ(θ)=cos²θ, de modo que 0≤λ≤1. La solución es

${\displaystyle \begin{array}{l}u=\frac{GM{m}^2}{L^2}\left\{\frac{{\sin }^4\theta }{3}+{\cos }^2\theta -\frac{{\cos }^4\theta }{3}\right\}+A\sin \theta +B\cos \theta \\ u=\frac{GM{m}^2}{L^2}\frac{1}{3}\left\{{\left(1-{\cos }^2\theta \right)}^2+3{\cos }^2\theta -{\cos }^4\theta \right\}+A\sin \theta +B\cos \theta \\ u=\frac{GM{m}^2}{L^2}\frac{1}{3}\left\{1+{\cos }^2\theta \right\}+A\sin \theta +B\cos \theta \end{array}}$

Condiciones iniciales

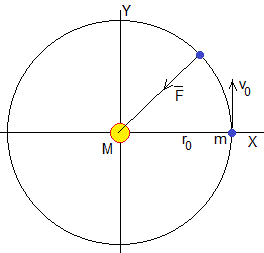
Supongamos que el cuerpo celeste de masa m describe una órbita circular de radio r₀ alrededor del centro de fuerzas fijo de masa M. Por la dinámica del movimiento circular uniforme

${\displaystyle \begin{array}{l}{v}_0=\sqrt{\frac{GM}{r_0}}\\ L=m{r}_0{v}_0\end{array}}$

• Como r=r₀ es constante, du/dθ=0, en el instante inicial. Calculamos la derivada de u

${\displaystyle \frac{du}{d\theta }=-\frac{1}{3}\frac{GM{m}^2}{L^2}\cos \theta \sin \theta +A\cos \theta -B\sin \theta }$

Para que du/dθ=0, se deberá cumplir que A=0

La ecuación de la trayectoria es

${\displaystyle u=\frac{1}{3}\frac{GM{m}^2}{L^2}\left\{1+{\cos }^2\theta \right\}+B\cos \theta }$

• La segunda condición inicial es que u=1/r₀ para θ=0

${\displaystyle \begin{array}{l}\frac{1}{r_0}=\frac{2}{3}\frac{GM{m}^2}{L^2}+B\\ \frac{1}{r_0}=\frac{2}{3}\frac{GM{m}^2}{m^2{v}_0^2{r}_0^2}+B\\ B=\frac{1}{3}\frac{1}{r_0}\end{array}}$

La ecuación de la trayectoria es

${\displaystyle \begin{array}{l}\frac{1}{r}=\frac{1}{3}\frac{1}{r_0}\left\{1+{\cos }^2\theta +\cos \theta \right\}\\ r=\frac{3r_0}{1+{\cos }^2\theta +\cos \theta }\end{array}}$

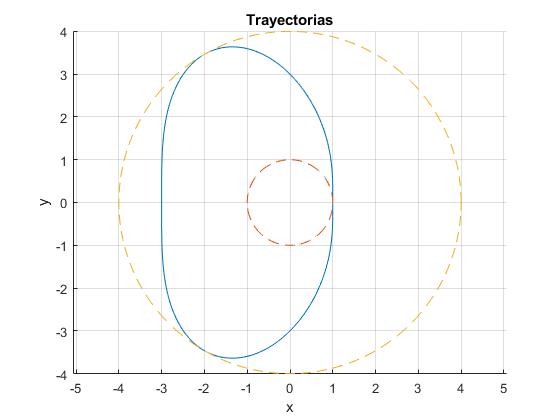
Representamos la trayectoria

r0=1;
r=@(x) 3./(1+cos(x).^2+cos(x));
hold on
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0,2*pi])
fplot(@(x) r0*cos(x), @(x) r0*sin(x),[0,2*pi], 'lineStyle','--')
fplot(@(x) 4*r0*cos(x), @(x) 4*r0*sin(x),[0,2*pi], 'lineStyle','--')
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title('Trayectorias')

Periodo

Dado que la fuerza es central, el momento angular permenece constante. Obtenemos el periodo a partir de la expresión del momento angular en coordenadas polares.

${\displaystyle \begin{array}{l}L=m{r}^2\frac{d\theta }{dt}\\ r^{2}d\theta =r_0{v}_0·dt\end{array}}$

Integramos

$\begin{array}{l}9r_0^2{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{d\theta }{{\left(1+{\cos }^2\theta +\cos \theta \right)}^2}}=r_0\sqrt{\frac{GM}{r_0}}{\displaystyle \underset{0}{\overset{P}{\int }}dt}\\ P=9\frac{r_0^{3/2}}{\sqrt{GM}}\frac{\pi \sqrt{2}·3^{1/4}\left(\sqrt{3}+1\right)}{3}=\frac{r_0^{3/2}}{\sqrt{GM}}\pi \sqrt{2}·3^{5/4}\left(\sqrt{3}+1\right)\end{array}$

Se ha utilizado Math Symbolic de MATLAB para obtener el resultado de la integral definida

>> syms x;
>> int(1/(1+cos(x)^2+cos(x))^2,x,0,2*pi)
 ans =(pi*2^(1/2)*3^(1/4)*(3^(1/2) + 1))/3

Referencias

Colin R. McInnes. Orbits in a Generalized Two-Body Problem. Journal of Guidance, Control and Dynamics, 26 (5) 2003. pp. 743-749. 'https://pure.strath.ac.uk/ws/portalfiles/portal/203650/strathprints006246.pdf'