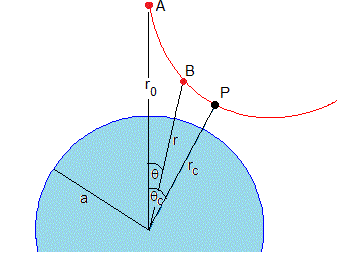
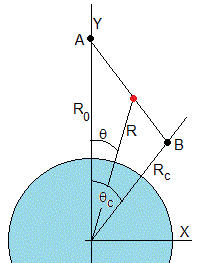
La Tierra tiene una masa M y un radio a. Supondremos que una partícula de masa m parte del reposo desde una distancia r₀>a al centro de la Tierra, tal como se muestra en la figura

Calcularemos la trayectoria que deberá seguir la partícula para que emplee un tiempo mínimo en llegar al punto P más cercano al superficie terrestre

Cuando la partícula se encuentra en B a una distancia r del centro de la Tierra, su velocidad v es

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+\left(-G\frac{Mm}{r}\right)=-G\frac{Mm}{r_0}\\ v=\sqrt{2GM\left(\frac{1}{r}-\frac{1}{r_0}\right)}\end{array}}$

El tiempo que tarda en desplazarse entre desde A(r₀,0) a B (r,θ) es

${\displaystyle t={\displaystyle \underset{A}{\overset{B}{\int }}\frac{ds}{v}}}$

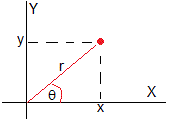
Expresamos $ds=\sqrt{d{x}^2+d{y}^2}$, en coordenadas polares

x=rcosθ, y=rsinθ

dx=dr·cosθ-rsinθ·dθ, dy=dr·sinθ+rcosθ·dθ

${\displaystyle ds=\sqrt{d{r}^2+r^{2}d{\theta }^2}=\sqrt{{\left(\frac{dr}{d\theta }\right)}^2+r^2}d\theta =\sqrt{{\dot{r}}^2+r^2}d\theta }$

El tiempo que tarda en desplazarse el móvil entre A y B expresado en coordendas polares es

${\displaystyle t(r)={\displaystyle \underset{A}{\overset{B}{\int }}\frac{\sqrt{{\dot{r}}^2+r^2}}{\sqrt{2GM\left(\frac{1}{r}-\frac{1}{r_0}\right)}}}d\theta =\frac{1}{\sqrt{2GM}}{\displaystyle \underset{A}{\overset{B}{\int }}\sqrt{\frac{r{r}_0\left({\dot{r}}^2+r^2\right)}{r_0-r}}}d\theta }$

Establecemos magnitudes adimensionales, de modo que R=r/a, g=GM/a² y $T=t\sqrt{\frac{2g}{a}}$

${\displaystyle T(r)={\displaystyle \underset{A}{\overset{B}{\int }}\sqrt{\frac{R{R}_0\left({\dot{R}}^2+R^2\right)}{R_0-R}}}d\theta }$

Tenemos que buscar la función R=R(θ) que haga la funcional T(r) extremo. Dado que el integrando, la función

${\displaystyle f(\theta ,R,\dot{R})=\sqrt{\frac{R{R}_0\left({\dot{R}}^2+R^2\right)}{R_0-R}}}$

no depende de θ, la ecuación de Euler-Lagrange se escribe

${\displaystyle \begin{array}{l}f-\dot{R}\frac{\partial f}{\partial \dot{R}}=\frac{1}{\sqrt{c}}\\ \sqrt{\frac{R{R}_0\left({\dot{R}}^2+R^2\right)}{R_0-R}}-\sqrt{\frac{R{R}_0}{R_0-R}}\frac{{\dot{R}}^2}{\sqrt{{\dot{R}}^2+R^2}}\frac{1}{\sqrt{c}}\\ \frac{dR}{d\theta }=\pm R\sqrt{\frac{c{R}_0{R}^3+R-R_0}{R_0-R}}\end{array}}$

Siendo c una constante a determinar por las condiciones de contorno. El signo adecuado es (-) ya que R disminuye con el ángulo θ

Trayectoria

El punto P, la distancia más cercana a la Tierra R_c (en unidades adimensionales) se obtiene derivando dR/dθ=0. La raíz real de la ecuación cúbica, cR₀R³+R-R₀=0

Las raíces de un polinomio se calculan mediante el comando roots de MATLAB, para una ecuación cúbica las raíces se puede calcular de forma exacta. Se ha creado una función raices_3, que calcula las raíces de la ecuación x³+ax²+bx+c=0. Si la ecuación, como es este el caso, tiene una raíz real y dos complejas conjugadas, la primera es la real

function x = raices_3(p)
    Q=(p(2)*p(2)-3*p(3))/9;
    R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
    x=zeros(3,1); %reserva memoria para un vector de tres elementos
    if (R*R)<(Q^3)
        tetha=acos(R/sqrt(Q^3));
        x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
        x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
        x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
    else
        A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
        if A==0
            B=0;
        else
            B=Q/A;
        end
        x(1)=(A+B)-p(2)/3;
        x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); %mejor que i
        x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
    end
end

Llamamos a la función raices_3 para calcular la raíz real de la ecuación

${\displaystyle R^3+\frac{1}{c{R}_0}R-\frac{1}{c}=0}$

R0=2;
c=0.5;
raiz=raices_3([1,0,1/(c*R0),-1/c]);
Rc=raiz(1);
display(Rc)

Rc =     1

Obtenemos la ecuación implícita de la trayectoria R=R(θ) en magnitudes adimensionales, integrando la ecuación diferencial de primer orden

${\displaystyle \theta ={\displaystyle \underset{R}{\overset{R_0}{\int }}\frac{1}{R}\sqrt{\frac{R_0-R}{c{R}^3{R}_0+R-R_0}}dR}}$

Para R=R_c obtenemos la otra coordenada θ_c del punto P más cercano a la superficie de la Tierra

R0=2;
c=0.5;
raiz=raices_3([1,0,1/(c*R0),-1/c]);
Rc=raiz(1);
f=@(x) sqrt((R0-x)./(c*R0*x.^3+x-R0))./x;
phi_c=integral(f,Rc,R0);
display(phi_c)

phi_c =    0.6054

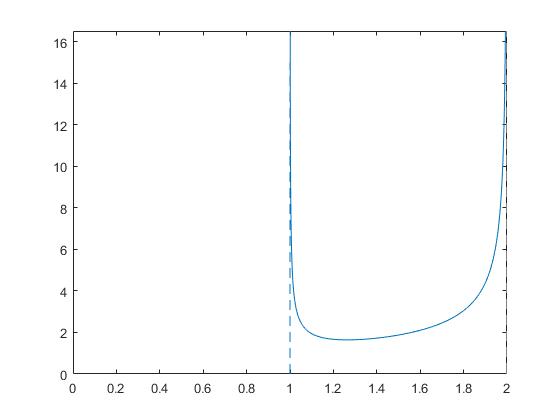
El integrando se hace infinito para el límite inferior R=R_c, sin embargo, MATLAB maneja adecuadamente este tipo de integral. Representamos el integrando en función de R

>> fplot(f,[Rc,R0])
>> line([Rc,Rc],[0,15],'linestyle','--')
>> xlim([0,R0])

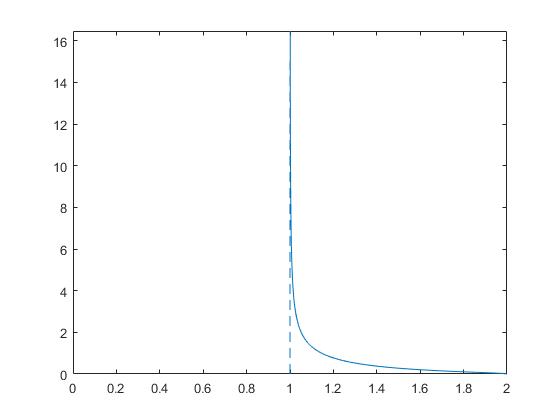
Dado el valor de la constante c obtenemos las coordendas de los puntos B(R,θ) por los que pasa la trayectoria en la que la partícula tarda un tiempo mínimo en desplazarse. En principio, es posible el problema inverso, dadas las coordenadas de un punto B calcular la constante c, resolviendo la ecuación trascendente, f(c)=0.

${\displaystyle \theta -{\displaystyle \underset{R}{\overset{R_0}{\int }}\frac{1}{R}\sqrt{\frac{R_0-R}{c{R}^3{R}_0+R-R_0}}dR}=0}$

Sin embargo, la función fzero de MATLAB, o el procedimiento de Newton dan errores provocados por valores complejos de la integral cuando el parámetro c desconocido está fuera de cierto rango

Una vez alcanzada la posición de retorno P, la partícula se mueve siguiendo una trayectoria simétrica hasta que alcanza la distancia R₀ en reposo haciendo un ángulo 2θ_c, tal como vemos en la figura al principio de esta página. Debido a la simetría, solamente es necesario calcular media trayectoria.

R0=2;
c=0.5;
raiz=raices_3([1,0,1/(c*R0),-1/c]);
Rc=raiz(1);
%trayectoria
f=@(x) sqrt((R0-x)./(c*R0*x.^3+x-R0))./x;
r=linspace(R0,Rc,100);
phi=zeros(0,length(r));
i=1;
for R=r
    phi(i)=integral(f,R,R0);
    i=i+1;
end
ang=[phi,2*phi(end)-fliplr(phi)];
rr=[r,fliplr(r)];
x=rr.*sin(ang);
y=rr.*cos(ang);
hold on
plot(x,y);

%punto P más cercano
x=Rc*sin(phi(end));
y=Rc*cos(phi(end));
plot(x,y,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
line([0,x],[0,y], 'linestyle','--')

%superficie de la Tierra
fplot(@(t) cos(t),@(t) sin(t),[0,2*pi])
hold off
grid on
axis equal
xlim([0,R0])
ylim([0,R0])
xlabel('x')
ylabel('y')
title('trayectoria de tiempo mínimo')

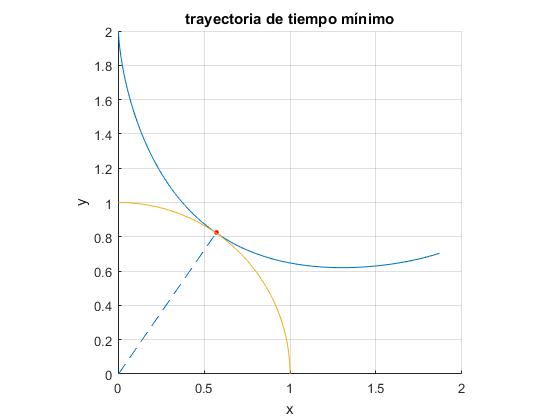
Tiempo de viaje

El tiempo (en unidades adimensionales) que tarda la partícula en viajar desde A(R₀,0) a B(R_c,θ_c)

${\displaystyle T={\displaystyle \underset{R_0}{\overset{R_c}{\int }}\sqrt{\frac{R{R}_0\left({\dot{R}}^2+R^2\right)}{R_0-R}}}d\theta }$

con

${\displaystyle \begin{array}{l}\dot{R}=\frac{dR}{d\theta }=-R\sqrt{\frac{c{R}_0{R}^3+R-R_0}{R_0-R}}\\ d\theta =-\frac{1}{R}\sqrt{\frac{R_0-R}{c{R}^3{R}_0+R-R_0}}dR\end{array}}$

Tenemos que integrar

${\displaystyle T={\displaystyle \underset{R_c}{\overset{R_0}{\int }}\frac{R^2}{\sqrt{\left(R_0-R\right)\left(c{R}^3{R}_0+R-R_0\right)}}dR}}$

La siguiente porción de código, nos proporciona las coordendas del punto B(R_c,θ_c) de llegada y el tiempo T que tarda en desplazarse desde A(R₀, 0) a B siguiendo la trayectoria que emplea un tiempo mínimo

R0=2;
c=0.5;
raiz=raices_3([1,0,1/(c*R0),-1/c]);
Rc=raiz(1);
f=@(x) sqrt((R0-x)./(c*R0*x.^3+x-R0))./x;
phi_c=integral(f,Rc,R0);
g=@(x) (x.^2)./sqrt((R0-x).*(c*R0*x.^3+x-R0));
T=integral(g,Rc,R0)*sqrt(c)*R0;
disp([Rc; phi_c;T])

    1.0000
    0.6054
    4.2099

El integrando se hace infinito en los dos límites de integración, pero el procedimiento integral de MATLAB consigue hallar su valor numérico, sin avisos ni errores

>> fplot(g,[Rc,R0])
>> xlim([0,R0])
>> line([Rc,Rc],[0,15],'linestyle','--')

Otras posibles trayectorias

Trayectoria rectilínea

Para que sirva de comparación, examinamos el tiempo que tarda la partícula en moverse desde el punto A(R₀, 0) a B(R_c,θ_c) siguiendo una trayectoria rectilínea bajo la única acción de la fuerza de atracción

La ecuación de la recta que une dos puntos A y B es

${\displaystyle \begin{array}{l}y=-\frac{R_0-R_c\cos {\theta }_c}{R_c\sin {\theta }_c}x+R_0\\ R\cos \theta =-\frac{R_0-R_c\cos {\theta }_c}{R_c\sin {\theta }_c}R\sin \theta +R_0\end{array}}$

Despejamos R y calculamos dR/dθ

${\displaystyle \begin{array}{l}R=\frac{R_0{R}_c\sin {\theta }_c}{R_c\sin \left({\theta }_c-\theta \right)+R_0\sin \theta }\\ \dot{R}=\frac{dR}{d\theta }=\frac{R_0{R}_c\sin {\theta }_c\left(R_c\cos \left({\theta }_c-\theta \right)-R_0\cos \theta \right)}{{\left(R_c\sin \left({\theta }_c-\theta \right)+R_0\sin \theta \right)}^2}\end{array}}$

Calculamos el tiempo T integrando por procedimientos numéricos

${\displaystyle \begin{array}{l}T={\displaystyle \underset{A}{\overset{B}{\int }}\sqrt{\frac{R{R}_0\left({\dot{R}}^2+R^2\right)}{R_0-R}}}d\theta \\ T=\sqrt{\left(R_c^2+R_0^2-2R_0{R}_c\cos {\theta }_c\right)R_0^3{R}_c^3{\sin }^3{\theta }_c}\\ {\displaystyle \underset{0}{\overset{{\theta }_c}{\int }}\frac{d\theta }{{\left(R_c\sin \left({\theta }_c-\theta \right)+R_0\sin \theta \right)}^2\sqrt{R_c\sin \left({\theta }_c-\theta \right)+R_0\sin \theta -R_c\sin {\theta }_c}}}\end{array}}$

R0=2;
c=0.5;
raiz=raices_3([1,0,1/(c*R0),-1/c]);
Rc=raiz(1);
f=@(x) sqrt((R0-x)./(c*R0*x.^3+x-R0))./x;
phi_c=integral(f,Rc,R0);
g=@(x) 1./(((Rc*sin(phi_c-x)+R0*sin(x)).^2).*
sqrt(Rc*sin(phi_c-x)+R0*sin(x)-Rc*sin(phi_c)));
T=integral(g,0,phi_c)*sqrt((Rc^2+R0^2-2*R0*Rc*cos(phi_c))*
R0^3*Rc^3*sin(phi_c)^3);
disp([Rc; phi_c;T])

    1.0000
    0.6054
    4.4124

Tarda un tiempo de 4.41 en recorrer la trayectoria rectilínea, mayor que tiempo mínimo 4.21 calculado en el apartado precedente

Caída del cuerpo

Finalizamos, comparando con el tiempo que tarda la partícula en caer radialmente desde la distancia R₀ a la distancia R_c partiendo del reposo. En la página titulada, Movimiento de dos cuerpos bajo la fuerza de atracción mutua, estudiamos esta situación, llegando a la expresión

${\displaystyle t=r_0\sqrt{\frac{r_0}{2GM}}\left\{\arccos \left(\sqrt{\frac{r_c}{r_0}}\right)+\sqrt{\frac{r_c}{r_0}}\sqrt{1-\frac{r_c}{r_0}}\right\}}$

Establecemos las mismas magnitudes adimensionales, de modo que R=r/a, g=GM/a² y $T=t\sqrt{\frac{2g}{a}}$, siendo a el radio de la Tierra

${\displaystyle T=R_0^{3/2}\left(\arccos \left(\sqrt{\frac{R_c}{R_0}}\right)+\sqrt{\frac{R_c}{R_0}}\sqrt{1-\frac{R_c}{R_0}}\right)}$

R0=2;
c=0.5;
raiz=raices_3([1,0,1/(c*R0),-1/c]);
Rc=raiz(1);
T=R0^(3/2)*(acos(sqrt(Rc/R0))+sqrt(Rc/R0)*sqrt(1-Rc/R0));
disp(T)

    3.6357

Referencias

Bani Singh, Raive Kumar. Brachistochrone problem in nonuniform gravity. Indian J. pure appl. Math. 19 (6): 575-585, June 1988