En la página titulada, La aceleración de la gravedad en el interior y en el exterior de una distribución esférica y uniforme de masa, calculamos la aceleración de la gravedad g en un punto P situado a una distancia r del centro de una distribución esférica y uniforme de masa de radio R.

A continuación, calculamos la energía potencial E_p(r) correspondiente a la fuerza conservativa mg(r) para r<R

${\displaystyle E_p(r)=-\frac{3}{2}\frac{GMm}{R}+\frac{GMm}{R^3}\frac{r^2}{2}}$

Ecuación de la trayectoria

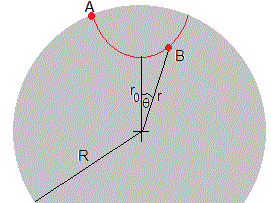
Una partícula de masa m parte en reposo de un punto A situado en la superficie de la Tierra y llega a B situado a una distancia r del centro de la Tierra, con velocidad v. Aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2-\frac{3}{2}\frac{GMm}{R}+\frac{GMm}{R^3}\frac{r^2}{2}=-\frac{GMm}{R}\hfill \\ v=\sqrt{\frac{GM}{R}\left(1-\frac{r^2}{R^2}\right)}\hfill \end{array}}$

El tiempo t que tarda en desplazarse una partícula entre A y B es

${\displaystyle t={\displaystyle \underset{A}{\overset{B}{\int }}\frac{ds}{v}}}$

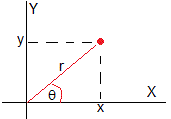
Expresamos $ds=\sqrt{d{x}^2+d{y}^2}$, en coordenadas polares

x=rcosθ, y=rsinθ

dx=dr·cosθ-rsinθ·dθ, dy=dr·sinθ+rcosθ·dθ

${\displaystyle ds=\sqrt{d{r}^2+r^{2}d{\theta }^2}=\sqrt{{\left(\frac{dr}{d\theta }\right)}^2+r^2}·d\theta =\sqrt{{\dot{r}}^2+r^2}·d\theta }$

El tiempo que tarda en desplazarse el móvil por el interior de la Tierra entre A y B expresado en coordenadas polares es

${\displaystyle t(r)={\displaystyle \underset{A}{\overset{B}{\int }}\frac{\sqrt{{\dot{r}}^2+r^2}}{\sqrt{\frac{GM}{R}\left(1-\frac{r^2}{R^2}\right)}}}d\theta =\sqrt{\frac{R^3}{GM}}{\displaystyle \underset{A}{\overset{B}{\int }}\frac{\sqrt{{\dot{r}}^2+r^2}}{\sqrt{R^2-r^2}}}d\theta }$

Tenemos que buscar la función r=r(θ) que haga la funcional t(r) extremo. Dado que el integrando, la función

${\displaystyle f(\theta ,r,\dot{r})=\frac{\sqrt{{\dot{r}}^2+r^2}}{\sqrt{R^2-r^2}}}$

no depende de θ, la ecuación de Euler-Lagrange se escribe

${\displaystyle \begin{array}{l}f-\dot{r}\frac{\partial f}{\partial \dot{r}}=C_1\\ \frac{r^2}{\sqrt{R^2-r^2}\sqrt{{\dot{r}}^2+r^2}}=C_1\end{array}}$

C₁ es una constante que se evalúa para el mínimo r₀ de la trayectoria r=r(θ), es decir, cuando dr/dθ=0

${\displaystyle r_0=\frac{C_1}{\sqrt{1+C_1^2}}R}$

En términos del nuevo parámetro r₀, la ecuación diferencial de la trayectoria se escribe

${\displaystyle \begin{array}{l}\frac{r^2}{\sqrt{R^2-r^2}\sqrt{{\dot{r}}^2+r^2}}=\frac{r_0}{\sqrt{R^2-r_0^2}}\\ \frac{dr}{d\theta }=r\frac{R}{r_0}\sqrt{\frac{r^2-r_0^2}{R^2-r^2}}\\ \frac{R}{r_0}\theta ={\displaystyle \int \sqrt{\frac{R^2-r^2}{r^2-r_0^2}}}\frac{dr}{r}+C_2\end{array}}$

Para calcular la integral hacemos el cambio de variable

${\displaystyle \begin{array}{l}u=\sqrt{\frac{r^2-r_0^2}{R^2-r^2}}r=\sqrt{\frac{r_0^2+R^2{u}^2}{1+u^2}}\\ dr=\frac{u}{r}\frac{R^2-r_0^2}{{(1+u^2)}^2}du\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{\displaystyle \int \sqrt{\frac{R^2-r^2}{r^2-r_0^2}}}\frac{dr}{r}={\displaystyle \int \frac{1}{r^2}\frac{R^2-r_0^2}{{(1+u^2)}^2}du}={\displaystyle \int \frac{\left(R^2-r_0^2\right)du}{\left(r_0^2+R^2{u}^2\right)\left(1+u^2\right)}}=\\ {\displaystyle \int \frac{\left(R^2+R^2{u}^2-R^2{u}^2-r_0^2\right)du}{\left(r_0^2+R^2{u}^2\right)\left(1+u^2\right)}}=R^2{\displaystyle \int \frac{du}{r_0^2+R^2{u}^2}}-{\displaystyle \int \frac{du}{1+u^2}}=\\ \frac{R}{r_0}{\tan }^{-1}\left(\frac{R}{r_0}u\right)-{\tan }^{-1}u=\frac{R}{r_0}{\tan }^{-1}\left(\frac{R}{r_0}\sqrt{\frac{r^2-r_0^2}{R^2-r^2}}\right)-{\tan }^{-1}\left(\sqrt{\frac{r^2-r_0^2}{R^2-r^2}}\right)\end{array}}$

La ecuación implícita de la trayectoria, r=r(θ), es

${\displaystyle \theta ={\tan }^{-1}\left(\frac{R}{r_0}\sqrt{\frac{r^2-r_0^2}{R^2-r^2}}\right)-\frac{r_0}{R}{\tan }^{-1}\left(\sqrt{\frac{r^2-r_0^2}{R^2-r^2}}\right)+C_2}$

Donde θ se mide desde el eje de simetría. Véase la figura al principio de la página

Para r=r₀, cuando r es mínimo, θ=0, por lo que C₂=0. Para r=R, cuando retorna a la superficie de la Tierra

${\displaystyle \theta =\frac{\pi }{2}-\frac{r_0}{R}\frac{\pi }{2}=\frac{\pi }{2}\left(1-\frac{r_0}{R}\right)}$

El ángulo subtendido por la trayectoria, entre las localidades de partida y destino en la superficie de la Tierra, por simetría, es el doble

${\displaystyle \Delta \theta =\pi \left(1-\frac{r_0}{R}\right)}$

Tiempo que tarda en recorrer el camino

Teniendo en cuenta que

${\displaystyle \dot{r}=\frac{dr}{d\theta }=r\frac{R}{r_0}\sqrt{\frac{r^2-r_0^2}{R^2-r^2}}}$

Calculamos la expresión del tiempo t

${\displaystyle \begin{array}{l}t=\sqrt{\frac{R^3}{GM}}{\displaystyle \int \frac{\sqrt{{\dot{r}}^2+r^2}}{\sqrt{R^2-r^2}}d\theta }=\sqrt{\frac{R}{GM}}\sqrt{R^2-r_0^2}{\displaystyle \int \frac{r·dr}{\sqrt{R^2-r^2}\sqrt{r^2-r_0^2}}}=\\ \sqrt{\frac{R}{GM}}\sqrt{R^2-r_0^2}{\displaystyle \int \frac{r·dr}{\sqrt{{\left(\frac{R^2-r_0^2}{2}\right)}^2-{\left(\frac{R^2+r_0^2}{2}-r^2\right)}^2}}}\end{array}}$

Llamando

${\displaystyle u=\frac{\left(\frac{R^2+r_0^2}{2}-r^2\right)}{\left(\frac{R^2-r_0^2}{2}\right)}du=-\frac{2r·dr}{\left(\frac{R^2-r_0^2}{2}\right)}}$

El resultado de la integral es

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{r·dr}{\sqrt{{\left(\frac{R^2-r_0^2}{2}\right)}^2-{\left(\frac{R^2+r_0^2}{2}-r^2\right)}^2}}}=-\frac{1}{2}{\displaystyle \int \frac{du}{\sqrt{1-u^2}}}=\frac{1}{2}{\cos }^{-1}u\\ \frac{1}{2}{\cos }^{-1}\left(\frac{R^2+r_0^2-2r^2}{R^2-r_0^2}\right)\end{array}}$

Tomando tiempo t=0, cuando la trayectoria pasa por el mínimo r=r₀

${\displaystyle \begin{array}{l}t=\frac{1}{2}\sqrt{\frac{R}{GM}}\sqrt{R^2-r_0^2}{{\cos }^{-1}\left(\frac{R^2+r_0^2-2r^2}{R^2-r_0^2}\right)|}_{r_0}^r=\\ \frac{1}{2}\frac{1}{\sqrt{Rg}}\sqrt{R^2-r_0^2}{\cos }^{-1}\left(\frac{R^2+r_0^2-2r^2}{R^2-r_0^2}\right)\end{array}}$

Finalmente, por simetría, el tiempo de viaje T es el doble del tiempo que tarda en ir del mínimo r₀ a R

${\displaystyle \begin{array}{l}T=2\frac{1}{2}\frac{1}{\sqrt{Rg}}\sqrt{R^2-r_0^2}{{\cos }^{-1}\left(\frac{R^2+r_0^2-2r^2}{R^2-r_0^2}\right)|}_{r_0}^R\\ T=\frac{1}{\sqrt{Rg}}\sqrt{R^2-r_0^2}\left(\pi -0\right)=\pi \sqrt{\frac{R}{g}}\sqrt{1-{\left(\frac{r_0}{R}\right)}^2}\end{array}}$

Ecuaciones paraméricas de la trayectoria

Llamando Ω=π/T, en la ecuación que nos da el tiempo t, despejamos r²

${\displaystyle \begin{array}{l}t=\frac{1}{2}\frac{1}{\sqrt{Rg}}\sqrt{R^2-r_0^2}{\cos }^{-1}\left(\frac{R^2+r_0^2-2r^2}{R^2-r_0^2}\right)\\ \frac{R^2+r_0^2-2r^2}{R^2-r_0^2}=\cos \left(2\Omega t\right)\\ r^2=\frac{1}{2}\left(R^2+r_0^2\right)-\frac{1}{2}\left(R^2-r_0^2\right)\cos \left(2\Omega t\right)\end{array}}$

Expresamos la posición angular θ en función del tiempo t.

${\displaystyle \begin{array}{l}\theta ={\tan }^{-1}\left(\frac{R}{r_0}\sqrt{\frac{r^2-r_0^2}{R^2-r^2}}\right)-\frac{r_0}{R}{\tan }^{-1}\left(\sqrt{\frac{r^2-r_0^2}{R^2-r^2}}\right)\\ \frac{r^2-r_0^2}{R^2-r^2}=\frac{1-\cos \left(2\Omega t\right)}{1+\cos \left(2\Omega t\right)}=\frac{2{\sin }^2\left(\Omega t\right)}{2{\cos }^2\left(\Omega t\right)}={\tan }^2\left(\Omega t\right)\\ \theta ={\tan }^{-1}\left(\frac{R}{r_0}\tan \left(\Omega t\right)\right)-\frac{r_0}{R}\Omega t\end{array}}$

Conocidos r y θ en función del tiempo t dibujamos la trayectoria. Hacemos que todos los viajes partan de la misma localidad situada en la superficie de la Tierra. Los puntos de destino, son localidades situadas en la superficie de la Tierra distantes, 30, 60, 90, 120°

hold on
delta=0;
for ang=(30:30:120)*pi/180
    r0=1-ang/pi;
    T=pi*sqrt(6371*1000/9.8)*sqrt(1-r0^2);
    r2=@(t) (1+r0^2)/2-(1-r0^2)*cos(2*pi*t/T)/2;
    th=@(t) atan(tan(pi*t/T)/r0)-r0*pi*t/T;
    x=@(t) sqrt(r2(t)).*cos(th(t)+delta);
    y=@(t) sqrt(r2(t)).*sin(th(t)+delta);
    fplot(x,y,[-T/2,T/2], 'displayName',num2str(ang*180/pi))
    delta=ang/2;
end
legend('-DynamicLegend','location','northwest')
fplot(@(t) cos(t),@(t) sin(t),[0,2*pi])
hold off
axis equal
grid on
xlabel('x');
ylabel('y')
title('el túnel más rápido')

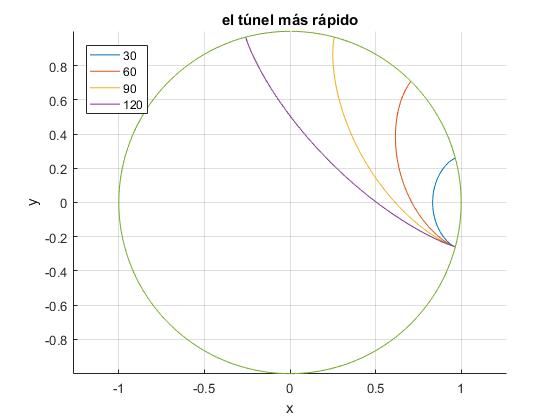
>>  T/60
ans =   39.8028

El viaje entre las dos localidades más alejadas, separadas un ángulo de 120° ha durado 39.8 minutos

Curvas cicloidales

El camino hallado es un arco de una curva denominada hipocicloide

${\displaystyle \{\begin{array}{l}x=\frac{a}{n}\left\{\left(n-1\right)\cos \phi -\cos \left((n-1)\phi \right)\right\}\\ y=\frac{a}{n}\left\{\left(n-1\right)\sin \phi +\sin \left((n-1)\phi \right)\right\}\end{array}}$

a=1;
n=5;
x=@(t) a*((n-1)*cos(t)-cos((n-1)*t))/n;
y=@(t) a*((n-1)*sin(t)+sin((n-1)*t))/n;
hold on
fplot(x,y,[0,2*pi])
fplot(@(t) a*cos(t),@(t) a*sin(t),[0,2*pi])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Hipotrocoide')

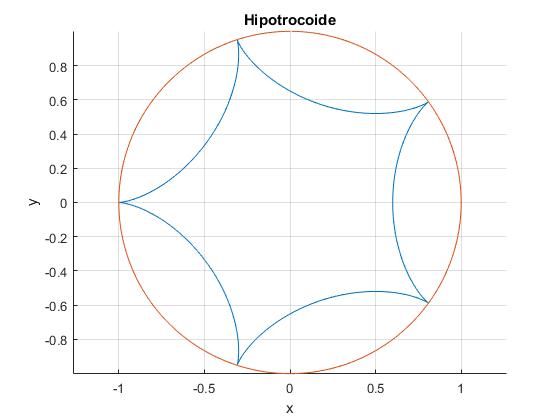
Se sugiere al lector cambiar el valor de n por ejemplo 2,3,4 (número entero), 5/3, 7/3, 8/3, 9/4 (número racional), π, $\sqrt{2}$, véase la página Hypocycloid

En el programa interactivo de la página titulada Curvas cicloidales se generan curvas denominadas epicicloidales. Se trata de curvas engendradas por un punto ligado a una círculo móvil que rueda sin deslizar sobre una circunferencia fija. Cuando el círculo móvil es interior a la circunferencia fija la curva engendrada recibe el nombre de hipocicloide.

Referencias

Giulio Venezian. Terrestrial Brachistochrone. Am. J. Phys. 34 (8) August 1966, 701

Priyanka Priyadarshini Mishra. Deriving And Deducing The Equation Of The Curve Of Quickest Descent. International Journal of Mathematics and its Applications. Volume 4, Issue 3-A (2016), 99-121