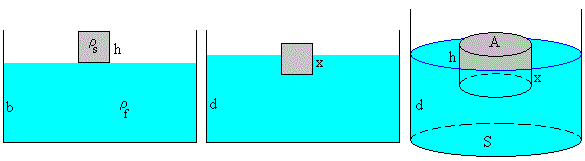
Supongamos un cuerpo en forma de paralepípedo de altura h, sección A y de densidad ρ_s. El fluido está contenido en un recipiente de sección S hasta una altura b. La densidad del fluido es ρ_f> ρ_s.

Se libera el cuerpo, oscila hacia arriba y hacia abajo, hasta que alcanza el equilibrio flotando sobre el líquido sumergido una longitud x.  El líquido del recipiente asciende hasta una altura d. Como la cantidad de líquido no ha variado S·b=S·d-A·x

${\displaystyle d=b+\frac{A}{S}x}$

Hay que calcular x, de modo que la energía potencial del sistema formado por el cuerpo y el fluido sea mínima.

Tomamos el fondo del recipiente como nivel de referencia de la energía potencial.

El centro de masa del cuerpo se encuentra a una altura d-x+h/2. Su energía potencial es E_s=(ρ_s·A·h)g(d-x+h/2)

${\displaystyle E_s={\rho }_{s}Ahg\left(b+\frac{A}{S}x-x+\frac{h}{2}\right)}$

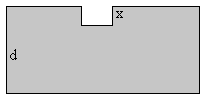
Para calcular el centro de masas del fluido, consideramos el fluido como una figura sólida de sección S y altura d a la que le falta una porción de sección A y altura x.

• El centro de masas de la figura completa, de volumen S·d es d/2

• El centro de masas del hueco, de volumen A·x, está a una altura (d-x/2)

${\displaystyle y_f=\frac{(Sd)(d/2)-(A·x)(d-x/2)}{Sd-Ax}=\frac{1}{Sb}\left\{\frac{1}{2}S{\left(b+\frac{A}{S}x\right)}^2+A\frac{x^2}{2}-Ax\left(b+\frac{A}{S}x\right)\right\}}$

La energía potencial del fluido es E_f=ρ_f(Sb)g·y_f

La energía potencial total es E_p=E_s+E_f

${\displaystyle \begin{array}{l}{E}_P=\frac{1}{2}{\rho }_{f}gA\left(1-\frac{A}{S}\right)x^2-{\rho }_{s}ghA\left(1-\frac{A}{S}\right)x+\frac{1}{2}{\rho }_{f}S{b}^{2}g+{\rho }_{s}hA\left(b+\frac{h}{2}\right)g=\\ \frac{1}{2}{\rho }_{f}gA\left(1-\frac{A}{S}\right)\left\{x^2-2\frac{{\rho }_s}{{\rho }_f}hx\right\}+\text{cte}\end{array}}$

El valor de la constante aditiva cte, depende de la elección del nivel de referencia de la energía potencial.

En la figura, se representa la energía potencial E_p(x) para un cuerpo de altura h=1.0, densidad ρ_s=0.4, parcialmente sumergido en un líquido de densidad ρ_f=1.0.

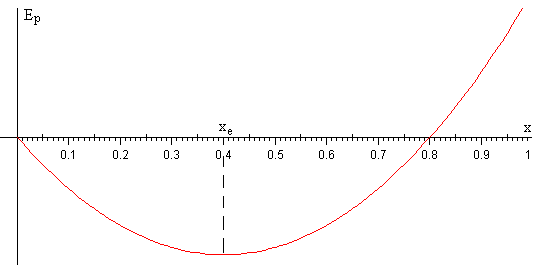
La función presenta un mínimo, que se calcula derivando la energía potencial con respecto de x e igualando a cero

${\displaystyle \frac{d{E}_p}{dx}=\frac{1}{2}{\rho }_{f}gA\left(1-\frac{A}{S}\right)\left\{2x-2\frac{{\rho }_s}{{\rho }_f}h\right\}=0}$

En la posición de equilibrio, el cuerpo se encuentra sumergido

${\displaystyle x_e=\frac{{\rho }_s}{{\rho }_f}h}$

Energía potencial de un cuerpo que se mueve en el seno de un fluido

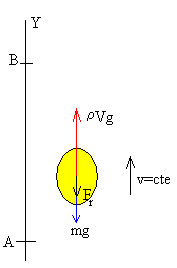
Cuando un globo de helio asciende en el aire actúan sobre el globo las siguientes fuerzas:

• El peso del globo $\overrightarrow{F_g}=-mg\widehat{j}$ .
• El empuje $\overrightarrow{F_e}={\rho }_{f}Vg\widehat{j}$ , siendo ρ_f  la densidad del fluido (aire).
• La fuerza de rozamiento F_r debida a la resistencia del aire

Dada la fuerza conservativa, la expresión de la energía potencial asociada, se obtiene integrando

${\displaystyle \underset{A}{\overset{B}{{\displaystyle \int }}}\overrightarrow{F}\cdot \overrightarrow{dr}=E_{pA}-E_{pB}{E}_p=E_p(y)}$

• La fuerza conservativa peso $\overrightarrow{F_g}=-mg\widehat{j}$ está asociada con la energía potencial E_g=mg·y.
• Por la misma razón, la fuerza conservativa empuje $\overrightarrow{F_e}={\rho }_{f}Vg\widehat{j}$ está asociada a la energía potencial E_e=-ρ_fVg·y.

Dada la energía potencial, obtenemos la expresión de la fuerza conservativa, derivando

${\displaystyle F_y=-\frac{d{E}_p\left(y\right)}{dy}}$

La energía potencial asociada con las dos fuerzas conservativas es

E_p=(mg- ρ_fVg)y

A medida que el globo asciende en el aire con velocidad constante experimenta una fuerza de rozamiento F_r debida a la resistencia del aire. La resultante de las fuerzas que actúan sobre el globo debe ser cero.

ρ_f Vg- mg-F_r=0

Como ρ_fVg> mg a medida que el globo asciende su energía potencial E_p disminuye.

Empleando el balance de energía obtenemos la misma conclusión

${\displaystyle \underset{A}{\overset{B}{{\displaystyle \int }}}\overrightarrow{F_{nc}}\cdot \overrightarrow{dr}={\left(E_k+E_p\right)}_B-{\left(E_k+E_p\right)}_A}$

El trabajo de las fuerzas no conservativas modifica la energía total (cinética más potencial) de la partícula. Como el trabajo de la fuerza de rozamiento es negativo y la energía cinética E_k no cambia (velocidad constante), concluimos que la energía potencial final E_pB es menor que la energía potencia inicial E_pA.

Energía potencial de un cuerpo parcialmente sumergido

En el apartado anterior, estudiamos la energía potencial de un cuerpo totalmente sumergido en un fluido (un globo de helio en la atmósfera). Ahora vamos a suponer un bloque cilíndrico que se sitúa sobre la superficie de un fluido (por ejemplo agua).

Pueden ocurrir dos casos:

• Que el bloque se sumerja parcialmente si la densidad del cuerpo sólido es menor que la densidad del fluido, ρ_s< ρ_f.
• Que el cuerpo se sumerja totalmente si ρ_s≥ ρ_f.

Cuando el cuerpo está parcialmente sumergido, sobre el cuerpo actúan dos fuerzas el peso mg=ρ_sSh·g que es constante y el empuje ρ_fSx·g que no es constante. Su resultante es

${\displaystyle \overrightarrow{F}=\left(-{\rho }_{s}Shg+{\rho }_{f}Sxg\right)\widehat{j}}$

Donde S el área de la base del bloque, h la altura del bloque y x la parte del bloque que está sumergida en el fluido.

Tenemos una situación análoga a la de un cuerpo que se coloca sobre un muelle elástico en posición vertical. La energía potencial gravitatoria mgy del cuerpo disminuye, la energía potencial elástica del muelle kx²/2 aumenta, la suma de ambas alcanza un mínimo en la posición de equilibrio, cuando se cumple –mg+kx=0, cuando el peso se iguala a la fuerza que ejerce el muelle.

${\displaystyle \begin{array}{l}{E}_p=mgy+\frac{1}{2}k{x}^2=mgy+\frac{1}{2}k{\left(y_0-y\right)}^2\\ F_y=-\frac{d{E}_p}{dy}=-mg+k\left(y_0-y\right)=-mg+kx\end{array}}$

El mínimo de E_p se obtiene cuando la derivada de E_p respecto de y es cero, es decir en la posición de equilibrio.

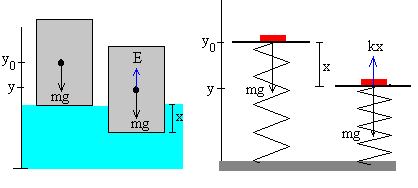
La energía potencial del cuerpo parcialmente sumergido será, de forma análoga

${\displaystyle \begin{array}{l}{E}_p={\rho }_{s}Shgy+\frac{1}{2}{\rho }_{f}Sg{x}^2={\rho }_{s}Shgy+\frac{1}{2}{\rho }_{f}Sg{\left(y_0-y\right)}^2\\ F_y=-\frac{d{E}_p}{dy}=-{\rho }_{s}Shg+{\rho }_{f}Sg\left(y_0-y\right)=-{\rho }_{s}Shg+{\rho }_{f}Sgx\end{array}}$

El mínimo de E_p se obtiene cuando la derivada de E_p respecto de y es cero, es decir, en la posición de equilibrio, cuando el peso se iguale al empuje. -ρ_sShg+ρ_fSxg=0

${\displaystyle x=\frac{{\rho }_{s}h}{{\rho }_f}=\rho h}$

El bloque permanece sumergido una longitud x. En esta fórmula, se ha designado ρ como la densidad relativa del sólido (respecto del fluido) es decir, la densidad del sólido tomando la densidad del fluido como la unidad.

Fuerzas sobre el bloque

1. Cuando ρ<1 o bien ρ_s<ρ_f, el cuerpo permanece parcialmente sumergido en la situación de equilibrio.
2. Cuando ρ>1 o bien ρ_s>ρ_f, el peso es siempre mayor que el empuje, la fuerza neta que actúa sobre el bloque es

F_y=-ρ_sShg+ρ_fShg<0.

No existe por tanto, posición de equilibrio, el bloque cae hasta que llega al fondo del recipiente que supondremos muy grande.

3. Cuando ρ=1 o bien ρ_s=ρ_f, el peso es mayor que el empuje mientras el bloque está parcialmente sumergido (x<h).

F_y=-ρ Shg+ρ Sxg<0.

La fuerza neta que actúa sobre el bloque cuando está completamente sumergido (x≥ h) es cero, y cualquier posición del bloque, completamente sumergido en el seno del fluido, es de equilibrio.

Curvas de energía potencial

1. La energía potencial correspondiente a la fuerza conservativa peso es

E_g=ρ_sShgy

2. La energía potencial correspondiente a la fuerza de empuje tiene dos partes



• Mientras el cuerpo está parcialmente sumergido (x<h)

${\displaystyle E_f=\frac{1}{2}{\rho }_{f}Sg{x}^2=\frac{1}{2}{\rho }_{f}Sg{\left(y_0-y\right)}^2}$

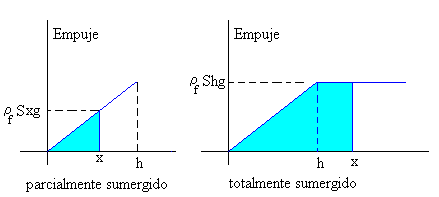
Que corresponde al área del triángulo de la figura de la izquierda.

• Cuando el cuerpo está totalmente sumergido (x≥h)

${\displaystyle E_f=\frac{1}{2}{\rho }_{f}Sg{h}^2+{\rho }_{f}Sgh\left(x-h\right)=-\frac{1}{2}{\rho }_{f}Sg{h}^2+{\rho }_{f}Sgh\left(y_0-y\right)}$

Que corresponde a la suma del área de un triángulo de base h, y la de un rectángulo de base x-h.

3. La energía potencial total es la suma de las dos contribuciones

E_p=E_g+E_f

Cuando la densidad del sólido es igual a la del fluido ρ_s=ρ_f, la energía potencial total E_p es constante e independiente de x (o de y) para x≥ h como puede comprobarse fácilmente.

Actividades

Se introduce

• La densidad del sólido ρ relativa al fluido en el control titulado Densidad relativa.

Se pulsa el botón titulado Nuevo.

El bloque tiene una altura h=1 y una sección S. Se coloca el bloque justamente encima de la superficie del fluido. La altura de su centro de masas es y₀=1.5 unidades.

Se suelta el bloque, llega hasta la posición final de equilibrio y_e=ρh, si la densidad ρ<1, o hasta el fondo del recipiente si la densidad ρ>1.

El programa interactivo no hace ninguna suposición acerca del modo en el que el bloque parte de la posición inicial y llega a la posición final (no calcula la posición y velocidad del cuerpo en cada instante), ya que el objetivo del programa es el de mostrar los cambios en la energía potencial E_p del cuerpo con la posición y del c.m. del mismo.

En la parte derecha, se traza:

• la energía potencial debida a la fuerza conservativa peso E_g (en color negro),
• la energía potencial debida al empuje E_f (en color azul)
• la suma de ambas contribuciones E_p (en color rojo) en función de la posición y del c.m. del bloque

La representación de la energía potencial gravitatoria E_g (en color negro) es una recta cuyo valor máximo está en la posición inicial y=1.5 y es cero cuando el bloque llega al fondo y=0.

La curva de la energía potencial correspondiente al empuje E_f (en color azul) es algo más complicada y consta de dos partes: Una parábola mientras el cuerpo está parcialmente sumergido (x<h) ó (y>0.5), unida a una línea recta cuando el cuerpo está completamente sumergido (x≥ h) ó (y≤ 0.5). La energía potencial inicial es cero y se va incrementando a medida que el cuerpo se sumerge en el fluido.

La curva de la energía potencial total E_p (en color rojo) es la suma de las dos contribuciones, E_p=E_g+E_f

Para trazar estas gráficas se ha tomado como unidad de energía, la energía potencial inicial del bloque ρ_sShg·y₀ con y₀=1.5, h=1 y ρ_s=ρ, densidad del sólido relativa al fluido ρ_f=1. De este modo, la energía potencial inicial del bloque es una unidad.

Se presentan tres casos:

1. Cuando ρ<1, la energía potencial presenta un mínimo en x=ρh. En este caso con x=y₀-y, h=1 e y₀=1.5, tendremos que la posición del c.m. en el equilibrio será y_e=1.5-ρ.

2. Cuando ρ>1, la curva de la energía potencial no tiene mínimo y por tanto, no hay posición de equilibrio estable.

3. En el caso límite en el que ρ=1 la energía potencial para y≤0.5 es una línea recta horizontal y la posición de equilibrio del c.m. del bloque puede ser cualquier y≤0.5.

Trabajo mínimo para extraer un cuerpo del seno de un fluido

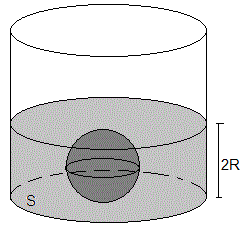
Una esfera de masa m, radio R y densidad ρ está completamente sumergida en un líquido de densidad ρ_l. Vamos a calcular el trabajo necesario para extraer la esfera completamente del líquido.

Cuando

Sección S del recipiente es muy grande

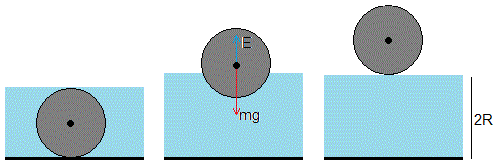
Supondemos inicialmente que la sección S del recipiente es muy grande, de modo que el líquido apenas cambia de nivel cuando se extrae completamente la esfera

Sobre la esfera actúan dos fuerzas: el peso mg y el empuje E. Como el centro la esfera se eleva 2R el trabajo realizado por el peso es

${\displaystyle W_P=-\rho \frac{4}{3}\pi R^{3}g\left(2R\right)=-\rho g\frac{8}{3}\pi R^4}$

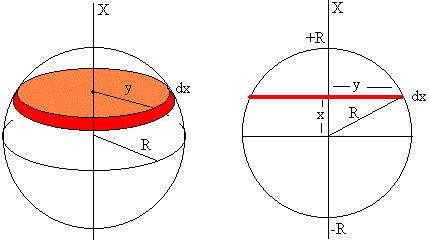
El empuje es el peso en líquido del volumen de la parte sumergida. Calculamos el volumen de la parte de la esfera sumergida en el líquido. Este volumen V es la suma (integral) de los elementos diferenciales de volumen de radio y y de altura dx, uno de los cuales se muestra en la figura.

${\displaystyle V={\displaystyle \underset{x}{\overset{R}{\int }}\pi y^{2}dx}={\displaystyle \underset{x}{\overset{R}{\int }}\pi (R^2-x^2)dx}=\frac{\pi R^3}{3}\left(2-3\frac{x}{R}+\frac{x^3}{R^3}\right)}$

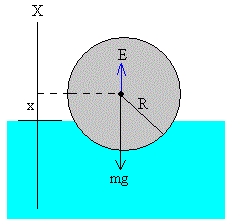
El empuje es E=ρ_lgV, el trabajo del empuje desde x=-R a x=R es

${\displaystyle \begin{array}{l}{W}_E={\displaystyle \underset{-R}{\overset{R}{\int }}\left({\rho }_{l}gV\right)dx=}{\rho }_{l}g\frac{\pi R^3}{3}{\displaystyle \underset{-R}{\overset{R}{\int }}\left(2-3\frac{x}{R}+\frac{x^3}{R^3}\right)dx}\\ W_E={\rho }_{l}g\frac{\pi R^3}{3}{\left(2x-\frac{3}{2}{x}^2+\frac{1}{4}\frac{x^4}{R^3}\right)|}_{-R}^R={\rho }_l\frac{4}{3}\pi R^{4}g\end{array}}$

El trabajo total es

${\displaystyle W=W_E+W_P=\frac{4}{3}\pi R^{4}g\left({\rho }_l-2\rho \right)=mg\left(\frac{{\rho }_l}{\rho }-2\right)R}$

El trabajo que tenemos que realizar para extraer la esfera es igual a W pero de signo contrario

La sección S del recipiente es pequeña

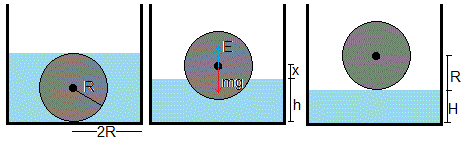
La sección del recipiente es S=π(2R)², circular de radio 2R

Al ascender la esfera, el nivel de líquido disminuye

El volumen de líquido es

${\displaystyle V_l=\pi {\left(2R\right)}^2·2R-\frac{4}{3}\pi R^3=\frac{20}{3}\pi R^3}$

Cuando el centro de la esfera se eleva x por encima de la superficie de líquido, la altura h de la superficie del líquido es

${\displaystyle \begin{array}{l}\pi {\left(2R\right)}^{2}h-\frac{\pi R^3}{3}\left(2-3\frac{x}{R}+\frac{x^3}{R^3}\right)=\frac{20}{3}\pi R^3\\ h=\frac{11}{6}R-\frac{1}{4}x+\frac{1}{12}\frac{x^3}{R^2}\end{array}}$

• Cuando x=-R, h=2R, situación inicial
• Cuando x=R, H=5R/3, situación final

La posición del centro de la esfera es

${\displaystyle \begin{array}{l}z=x+h=\frac{11}{6}R+\frac{3}{4}x+\frac{1}{12}\frac{x^3}{R^2}\\ dz=\left(\frac{3}{4}+\frac{1}{4}\frac{x^2}{R^2}\right)dx\end{array}}$

• Trabajo de la fuerza de empuje

El trabajo de la fuerza de empuje se calcula entre z=R y z=R+H, o bien, entre x=-R y x=R

${\displaystyle \begin{array}{l}{W}_E={\displaystyle \underset{R}{\overset{R+H}{\int }}\left({\rho }_{l}gV\right)dz=}{\rho }_{l}g\frac{\pi R^3}{3}{\displaystyle \underset{-R}{\overset{R}{\int }}\left(2-3\frac{x}{R}+\frac{x^3}{R^3}\right)\left(\frac{3}{4}+\frac{1}{4}\frac{x^2}{R^2}\right)dx=}\\ {\rho }_{l}g\frac{\pi R^3}{3}{\displaystyle \underset{-R}{\overset{R}{\int }}\left(\frac{3}{2}-\frac{9}{4}\frac{x}{R}+\frac{1}{2}\frac{x^2}{R^2}+\frac{1}{4}\frac{x^5}{R^5}\right)dx=}{\rho }_l\frac{\pi R^3}{3}g{\left(\frac{3}{2}x-\frac{9}{8}\frac{x^2}{R}+\frac{1}{6}\frac{x^3}{R^2}+\frac{1}{24}\frac{x^6}{R^5}\right)|}_{-R}^R=\frac{10}{9}{\rho }_l\pi R^{4}g\end{array}}$

• Trabajo del peso, es

${\displaystyle W_P=-\rho \frac{4}{3}\pi R^{3}g\left(R+H-R\right)=-\frac{20}{9}\rho g\pi R^4}$

El trabajo total es

${\displaystyle \begin{array}{l}W=W_E+W_P=\frac{10}{9}{\rho }_l\pi R^4-\frac{20}{9}\rho g\pi R^4=\frac{4}{3}\pi R^4\left(\frac{5}{3}R\right)\rho g\left(\frac{1}{2}\frac{{\rho }_l}{\rho }-1\right)\\ W=mgH\left(\frac{1}{2}\frac{{\rho }_l}{\rho }-1\right)\end{array}}$

El trabajo que tenemos que realizar para extraer la esfera es igual a W pero de signo contrario

Variación de energía potencial

En la situación inicial, el centro de masas de la esfera y del líquido se encuentra a una altura R. La energía potencial de la esfera y del líquido en la situación es

${\displaystyle E_1=\rho \left(\frac{4}{3}\pi R^3\right)gR+{\rho }_l\left(\frac{20}{3}\pi R^3\right)gR=\pi R^{4}g\left(\frac{4}{3}\rho +\frac{20}{3}{\rho }_l\right)}$

En la situación final, el centro de la esfera se encuentra a un altura (R+H)=(R+5R/3)=8R/3 y el centro de masas del líquido a una altura H/2=5R/6

${\displaystyle E_2=\rho \left(\frac{4}{3}\pi R^3\right)g\left(\frac{8}{3}R\right)+{\rho }_l\left(\frac{20}{3}\pi R^3\right)g\left(\frac{5}{6}R\right)=\pi R^{4}g\left(\frac{32}{9}\rho +\frac{50}{9}{\rho }_l\right)}$

La diferencia es

${\displaystyle \begin{array}{l}\Delta E_p=E_2-E_1=\pi R^{4}g\left(\frac{32}{9}\rho +\frac{50}{9}{\rho }_l\right)-\pi R^{4}g\left(\frac{4}{3}\rho +\frac{20}{3}{\rho }_l\right)=\pi R^{4}g\left(\frac{20}{9}\rho -\frac{10}{9}{\rho }_l\right)=\\ \rho \frac{4}{3}\pi R^{3}g\left(\frac{5}{3}R\right)\left(1-\frac{1}{2}\frac{{\rho }_l}{\rho }\right)=mgH\left(1-\frac{1}{2}\frac{{\rho }_l}{\rho }\right)\end{array}}$

El trabajo realizado por el peso y el empuje es igual a la variación de energía potencial cambiada de signo

Referencias

Reed B. C. Archimedes' law sets a good energy-minimization example. Physics Education, 39 (4) July 2004, pp. 322-323.

Keeports D. How does the potencial energy of a rising helium-filled balloon change?. The Physics Teacher, Vol 40, March 2002, pp. 164-165.

Silva A., Archimedes' law and the potential energy: modelling and simulation with a sreadsheet. Phys. Educ. 33 (2) March 1998. pp. 87-92.

REN Bao-wen. The minimum work for picking out an object from water in a container. College Physics. Volume 29, Issue 5, 20 May 2010