El punto de sujeción está por encima de la superficie del agua

Supongamos que el extremo P de la varilla está a una altura y>0 sobre la superficie del agua y en esa posición la varilla hace un ángulo θ con el eje vertical.

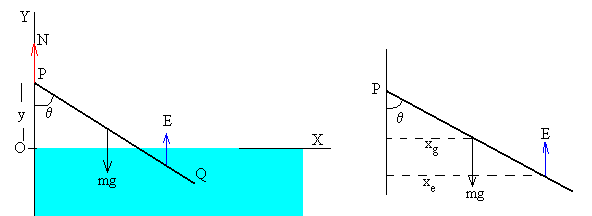
Las fuerzas que actúan sobre la varilla son:

• El peso mg=ρALg, actúa en el centro de masa de la varilla, en la posición cuya abscisa es

x_g=L/2·sinθ.

• La fuerza de empuje, E=gA·(L-y/cosθ) actúa en el centro de la porción de varilla sumergida, en la posición cuya abscisa es

${\displaystyle x_e=\left(\frac{y}{\cos \theta }+\frac{1}{2}\left(L-\frac{y}{\cos \theta }\right)\right)\sin \theta =\frac{1}{2}\left(L+\frac{y}{\cos \theta }\right)\sin \theta }$

• La reacción N se aplica en el punto P.

La barra estará en equilibrio:

• Si la resultante de todas las fuerzas es cero,

N+E=mg

• Si el momento de las fuerzas respecto del punto P es cero.

E·x_e-mgx_g+N·0=0

${\displaystyle gA\left(L-\frac{y}{\cos \theta }\right)\left(L+\frac{y}{\cos \theta }\right)\frac{\sin \theta }{2}-\rho gAL\frac{L}{2}\sin \theta =0}$

Simplificando, nos queda la ecuación

${\displaystyle \left(1-\rho -\frac{y^2}{L^2}\frac{1}{{\cos }^2\theta }\right)\sin \theta =0}$

Si y>L el primer factor entre paréntesis es distinto de cero. La posición de equilibrio se obtiene cuando sinθ=0, es decir, θ=0. La barra cuelga verticalmente del punto P, sin estar sumergida

Cuando y<L el primer término puede hacerse cero cuando

${\displaystyle \cos \theta =\frac{y}{L}\frac{1}{\sqrt{1-\rho }}\le 1}$

y como el coseno tiene que ser menor o igual que la unidad se tiene que cumplir a la vez que $y\le L\sqrt{1-\rho }$ Cuando no se cumple esta condición el primer factor no es nulo y la posición de equilibrio es θ=0.

El punto de sujeción está por debajo de la superficie del agua

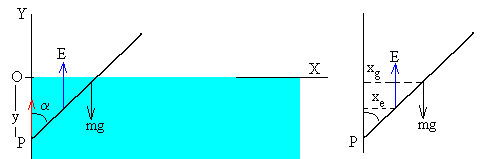
Sea y la distancia (positiva) del punto P de sujeción de la varilla al origen O

• El peso mg=ρALg, actúa en el centro de masa de la varilla, en la posición cuya abscisa es

x_g=L/2·sinα.

La fuerza de empuje, E=gA(y/cosα) actúa en el centro de la porción de varilla sumergida,  en la posición de abscisa

${\displaystyle x_e=\frac{1}{2}\frac{y}{\cos \alpha }\sin \alpha }$

Para que la varilla esté en equilibrio, el momento de estas fuerzas respecto del punto P es cero.

E·x_e-mgx_g=0

${\displaystyle gA\frac{y}{\cos \alpha }\frac{y}{\cos \alpha }\frac{\text{sin}\alpha }{2}-\rho gAL\frac{L}{2}\text{sin}\alpha =0}$

Simplificando

${\displaystyle \left(\frac{y^2}{L^2}\frac{1}{{\cos }^2\alpha }-\rho \right)\text{sin}\alpha =0}$

Si y>L el primer factor entre paréntesis no puede ser cero. La posición de equilibrio se obtiene cuando senα=0, es decir, α=0.

Cuando y<L el primer factor puede ser cero cuando

${\displaystyle \cos \alpha =\frac{y}{L}\frac{1}{\sqrt{\rho }}\le 1}$

y como el coseno tiene que ser menor o igual que la unidad se tiene que cumplir a la vez que $y\le L\sqrt{\rho }$ Cuando no se cumple esta condición el primer factor no es nulo y la posición de equilibrio es α=0.

Equilibrio de la varilla

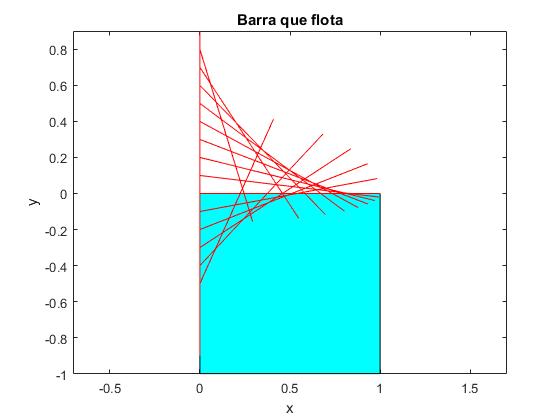
Vamos a representar la varilla a medida que se cambia la posición y del punto de sujeción P.

Los ángulos de equilibrio θ que forma la varilla con la dirección vertical, son

%L=1, longitud de la varilla
rho=0.3; %densidad
x_area=[0,1,1,0];  %agua
y_area=[0,0,-1,-1];
fill(x_area,y_area,'c')
%calcula el ángulo, que hace la varilla con la vertical
a=sqrt(1-rho);
b=sqrt(rho);
for y=-0.9:0.1:0.9
    if (y>0)
        if (y<a)
            angulo=acos(y/a);
        else
            angulo=0;
        end
    else
        if abs(y)<b
            angulo=acos(y/b);
        else
            angulo=pi;
        end
    end
   line([0,sin(angulo)],[y,y-cos(angulo)], 'color','r');
end
axis equal
xlabel('x')
ylabel('y')
title('Barra que flota')

Actividades

Se introduce

• La densidad ρ de la varilla, en el control titulado Densidad barra

• La posición y del punto P de sujeción de la varilla, en el control titulado Posición

• La longitud de la varilla se ha fijado en el programa interactivo en el valor L=1.0

Se pulsa el botón titulado Nuevo

Observamos, la varilla en su posición de equilibrio. Se muestran las fuerzas, peso de la varilla y fuerza de empuje sobre la parte sumergida.

En la parte derecha, se representa el ángulo θ, (en grados) en función de la posición y del punto de sujeción. Se representa mediante un punto el estado de equilibrio, el par de valores (y, θ).

Fijamos la densidad de la varilla, y vamos cambiando la posición y del punto P de sujeción de la varilla.

Ejemplo:

Introducimos los siguientes datos

• Densidad ρ=0.3
• Posición y=-0.4 del punto P de sujeción de la varilla.

Se pulsa el botón titulado Nuevo

Como y<0, comprobamos que se cumple la condición

${\displaystyle \left|y\right|\le L\sqrt{\rho }\text{0}\text{.4}<\text{1}\text{.0}\sqrt{\text{0}\text{.3}}}$

El ángulo θ que forma la varilla con el eje vertical se obtiene de la expresión

${\displaystyle \cos \theta =\frac{y}{L}\frac{1}{\sqrt{\rho }}\cos \theta =\frac{-0.4}{1.0}\frac{1}{\sqrt{0.3}}\theta =137º}$

Referencias

Duffy B. A bifurcation problem in hydrostatics. Am. J. Phys. 61 (3) March 1993, pp. 264-269