El ludión o diablillo de Descartes

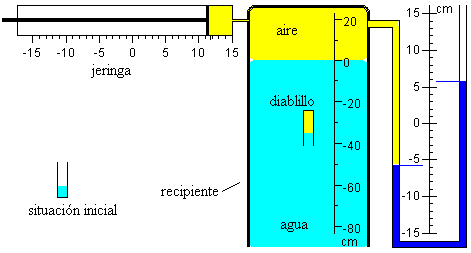
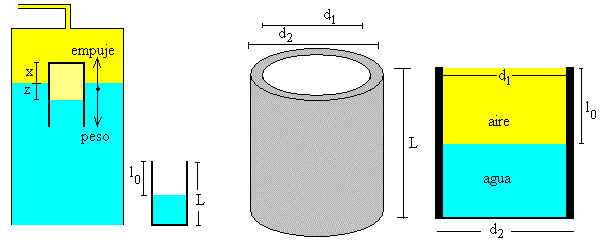
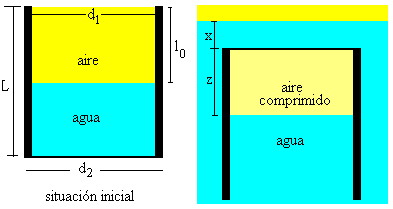
El diablillo o ludión es un tubo de ensayo de longitud L, de diámetro interior d₁ y de diámetro exterior d₂ que se llena parcialmente de agua hasta una altura L-l₀. Luego, se invierte en un recipiente grande que contiene agua, que está cerrado y conectado por una parte, a un manómetro para medir la presión del aire encerrado en su interior y por otra, a una jeringa que nos permite variar la presión P del aire del recipiente.

Estática del diablillo

En este apartado, estudiaremos el equilibrio del tubo de ensayo (diablillo) con la burbuja de aire dentro

Control de la presión

Para variar la presión del aire contenido en el recipiente se emplea una jeringa. Si el volumen total de aire del recipiente y de la jeringa es V₀. Al disminuir en x el volumen de la jeringa la presión aumenta de P₀ a P. Si suponemos una transformación isotérmica, tendremos que:

P(V₀-x)=P₀·V₀

Si x<<V₀ hacemos la siguiente aproximación

$P = \frac{P_{0}}{1 - x / V_{0}} = P_{0} {(1 - \frac{x}{V_{0}})}^{- 1} \approx P_{0} (1 + \frac{x}{V_{0}})$

El incremento de presión ΔP=P-P₀ es proporcional a la variación del volumen x de la jeringa o bien, al desplazamiento de su émbolo.

El tubo de ensayo

Después de haber invertido el tubo de ensayo dentro del agua del recipiente, la longitud de la burbuja de aire que se ha formado en el interior del tubo invertido es l=x+z

La base del tubo se encuentra a una altura x por encima de la superficie del agua del recipiente y el agua en el tubo se encuentra a una altura z por debajo de dicha superficie tal como se indica en la primera figura.

Sobre el tubo actúan dos fuerzas: el peso y el empuje

El peso

El peso del tubo es igual a la densidad del vidrio multiplicado por el volumen del tubo, un recipiente en forma de capa cilíndrica de diámetro interior d₁ y exterior d₂.

$V = \frac{π}{4} (d_{2}^{2} - d_{1}^{2}) L$

despreciamos el volumen de la base del tubo.

El área interior A del tubo de vidrio es

$A = \frac{π}{4} d_{1}^{2}$

El peso del tubo de vidrio es el producto de la densidad del vidrio ρ_v, por el volumen V de la capa cilíndrica de vidrio y por la aceleración de la gravedad g,

ρ_v·V·g

El empuje

El empuje no admite una expresión única y es distinta

Cuando el tubo está parcialmente sumergido x>0
Cuando el tubo está completamente sumergido x≤0

Analizaremos cada uno de los casos por separado

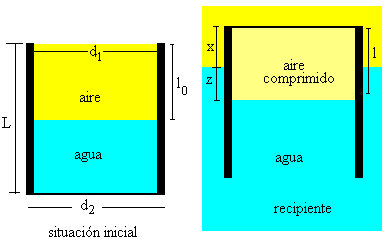
Cuando el tubo está parcialmente sumergido x>0

Empuje

En el primer caso, el empuje se compone de la suma de dos términos:

El empuje del tubo de vidrio que está parcialmente sumergido una longitud L-x.

ρ·g·V(1-x/L)

El empuje de la burbuja de aire que ha desalojado el agua contenida en el volumen cilíndrico de área A (el área de la sección trasversal del tubo) y de altura z.

ρ·g·A·z

La resultante es la diferencia entre el empuje y el peso

$F = ρ g A z + ρ g V (1 - \frac{x}{L}) - ρ_{v} g V$ (1)

Siendo ρ=1000 kg/m³ la densidad del agua, g=9.8 m/s² la aceleración de la gravedad, y ρ_v la densidad del vidrio, aproximadamente 2300 kg/m³.

Transformación isoterma

La ecuación fundamental de la estática de fluidos nos permite calcular la presión del aire en la burbuja, que es la presión existente a una profundidad z por debajo de la superficie del agua contenida en el recipiente

P+ρgz

Siendo P la presión del aire en el recipiente.

Si suponemos que en todo momento la temperatura permanece constante, aplicamos la ecuación de los gases ideales a la burbuja de aire:

En la situación inicial, con el tubo en la posición derecha, tenemos un volumen de aire A·l₀ a la presión atmosférica P₀
En la situación final, con el tubo en la posición invertida dentro del recipiente, tenemos una burbuja de aire cuyo volumen es A·(x+z) a la presión P+ρgz.

Se cumplirá que

P₀·l₀=(P+ρgz)·(x+z) (2)

Situación de equilibrio

El tubo permanece en equilibrio cuando el peso se igual al empuje o bien, cuando F=0.

Conocida la presión P determinamos x y z resolviendo un sistema de dos ecuaciones (1) y (2) con dos incógnitas.

De la segunda ecuación despejamos x

$x = \frac{P_{0} l_{0}}{P + ρ g z} - z$ (3)

y la sustituimos en la primera, para despejar z, quedando una ecuación de segundo grado, az²+bz+c=0, con

$\begin{array}{l} a = ρ^{2} g (\frac{V}{L} + A) \\ b = ρ P (\frac{V}{L} + A) - (ρ_{v} - ρ) V ρ g \\ c = - \frac{V}{L} ρ P_{0} l_{0} - (ρ_{v} - ρ) V P \end{array}$

Se calcula la raíz positiva de la ecuación de segundo grado

$z = \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a}$

Una vez que se ha calculado z, se determina mediante la ecuación (3), la posición de equilibrio x de la parte superior del tubo de ensayo.

Presión crítica.

Si se incrementa la presión hasta un valor límite P, el tubo de ensayo se va sumergiendo en el agua hasta que la posición de la parte superior del tubo está en el origen x_e=0. Si incrementamos un poco más la presión el tubo se hunde completamente.

La presión crítica P se determina poniendo x=0, en la ecuación (1) con F=0 (situación de equilibrio) y despejando P en la ecuación (2).

$z = \frac{V}{A} (\frac{ρ_{v}}{ρ} - 1) P = P_{0} \frac{l_{0}}{z} - ρ g z$

El tamaño z de la burbuja es independiente de su tamaño l₀ inicial, solamente depende de la geometría del tubo de ensayo, de la densidad del vidrio ρ_v y del agua ρ

Ejemplo

En el programa interactivo más abajo, se introduce

El tipo de tubo que se va a usar en la experiencia, en el control titulado Tubos

Se pulsa en el botón titulado Nuevo

Se modifica la altura l₀ inicial de la burbuja de aire en el tubo, moviendo con el puntero del ratón el círculo de color rojo, situada al lado de la imagen amplificada del tubo.
Se modifica la presión ΔP=P-P₀ en mm de mercurio, del aire contenido en el recipiente, en el control titulado Presión.
Se pone 0 en el control titulado Velocidad

Observaremos el tubo en la posición de equilibrio estable F=0, si es que existe. En caso contrario, un mensaje nos lo indica.

Al lado del tubo, se muestran dos vectores que representan el peso y al empuje, y en la parte superior del recipiente, se muestra el valor de la fuerza F.

Datos de los tubos utilizados, tomados del artículo citado en las referencias

Tubo	Altura L (cm)	Diámetro interior d₁(cm)	Diámetro exterior d₂ (cm)	Densidad ρ_v (g/cm³)
1	9.8	1.38	1.6	2.35
2	16.0	1.43	1.64	2.29
3	17.1	4.44	4.97	2.16
4	20.1	1.74	2.00	2.17

La presión atmosférica es P₀=101300 Pa. La densidad del mercurio (Hg) es 13.55 g/cm³

Ejemplo de presión crítica con el Tubo 2.

Calculamos la presión crítica para los estados iniciales siguientes:

Altura inicial l₀ de la burbuja de aire en cm	Presión crítica P (Pa)	Diferencia de presión ΔP=P-P₀ en mm de Hg
4	61632	-299
6	92766	-64
8	123901	170

Los datos de la última columna son los que se introducen en el control titulado Presión cuando se establece con el ratón la altura inicial l₀ de la primera columna, en el programa interactivo al final de la página. La velocidad inicial deberá ser cero, en el control titulado Velocidad

L=16/100; %longitud
d_int=1.43/100; %diámetro interior
d_ext=1.64/100; %diámetro exterior
V=pi*L*(d_ext^2-d_int^2)/4;
A=pi*d_int^2/4;
rho=1000; %densidad agua
rho_g=2.29*1000; %densidad vidrio
P0=1.013e5; %presión atmosférica
for l0=(4:2:8)/100
    z=V*(rho_g/rho-1)/A;
    P=P0*l0/z-rho*9.8*z;
    disp([P,(P-P0)*1000/(13550*9.8)])
end

   1.0e+04 *    6.1632   -0.0299
   1.0e+04 *    9.2766   -0.0064
   1.0e+05 *    1.2390    0.0017

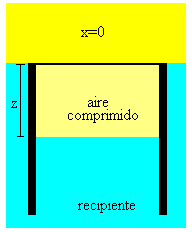
Cuando el tubo está completamente sumergido x≤0

Empuje

El empuje se compone de la suma de dos términos:

El empuje del tubo de vidrio que ahora está completamente sumergido

ρ·g·V

El empuje de la burbuja de aire que ha desalojado el agua contenida en el volumen cilíndrico de área A (el área de la sección trasversal del tubo) y de altura z.

ρ·g·A·z

La resultante de las fuerzas que actúan sobre el tubo es la diferencia entre el empuje y el peso

F=ρgAz+ρgV- ρ_vgV

Transformación isoterma

La presión del aire contenido en la burbuja es, para x<0

P+ρg(z+|x|)=P+ρg(z-x)

Suponiendo que el aire experimenta una transformación isotérmica entre el estado inicial y el final, tendremos

P₀·l₀= (P+ρg(z-x))z

Dinámica del diablillo

Escribimos, de nuevo, la fuerza que actúa sobre el tubo de ensayo

$F = {\begin{cases} ρ g A z + ρ g V (1 - x / L) - ρ_{v} g V x > 0 \\ ρ g A z + ρ g V - ρ_{v} g V x \leq 0 \end{cases}$

Relacionamos z y x mediante la ley de Boyle

$P_{0} l_{0} = {\begin{cases} (P + ρ g z) (z + x) x > 0 \\ (P + ρ g (z - x)) z x \leq 0 \end{cases}$

Tenemos que despejar z de las ecuaciones de segundo grado

$\begin{array}{l} ρ g z^{2} + (P + ρ g x) z + P x - P_{0} l_{0} = 0 x > 0 \\ ρ g z^{2} + (P - ρ g x) z - P_{0} l_{0} = 0 x \leq 0 \\ z = \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a} \\ a = ρ g b = {\begin{cases} P + ρ g x \\ P - ρ g x \end{cases} c = {\begin{cases} P x - P_{0} l_{0} x > 0 \\ - P_{0} l_{0} x \leq 0 \end{cases} \end{array}$

La fuerza F es ahora, una función de la posición x de la base del tubo de ensayo invertido

Para x>0

$F = ρ g V (1 - \frac{x}{L}) - ρ_{v} g V + \frac{A}{2} (- P + ρ g x + \sqrt{{(ρ g x - P)}^{2} + 4 ρ g P_{0} l_{0}})$

La fuerza F depende de la posición x, se trata de una fuerza conservativa cuya energía potencial se calcula del siguiente modo

$\int_{x_{e}}^{x} F d x = E_{p} (x_{e}) - E_{p} (x)$

Donde x_e es la posición de equilibrio al cual le vamos a asignar una energía potencial cero. Establecemos por tanto, en esta posición el nivel cero de energía potencial E_p(x_e)=0.

Para x>0 tenemos que hacer la integral

$\begin{array}{l} E_{1} (x) = - \int F (x) d x + C_{1} \\ E_{1} (x) = \frac{ρ g}{2} (\frac{A}{2} + \frac{V}{L}) x^{2} + (\frac{A P}{2} + V (ρ_{v} - ρ)) x - \frac{A}{2} f (x) + C_{1} \end{array}$

donde C₁ es una constante de integración que se determina a partir de la condición de que E₁(x_e)=0, f(x) es una función que se define más abajo.

Para x≤0

La fuerza es

$F = - (ρ_{v} - ρ) g V + \frac{A}{2} (- P - ρ g x + \sqrt{{(ρ g x - P)}^{2} + 4 ρ g P_{0} l_{0}})$

Para calcular la energía potencial, tenemos que hacer la integral

$\begin{array}{l} E_{2} (x) = - \int F (x) d x + C_{2} \\ E_{2} (x) = - \frac{A ρ g}{4} x^{2} + (\frac{A P}{2} + V (ρ_{v} - ρ)) x - \frac{A}{2} f (x) + C_{2} \end{array}$

La fuerza F es una función discontinua en x=0, pero la energía potencial E_p(x) es una función continua de modo que, en x=0 se tiene que cumplir que E₁(0)=E₂(0), esta condición determina el valor de la constante C₂ de integración.

La función f(x) es una integral que no es inmediata

$f (x) = \int \sqrt{{(ρ g x - P)}^{2} + 4 ρ g P_{0} l_{0}} \cdot d x$

Esta integral se puede escribir de la forma

$4 P_{0} l_{0} \int \sqrt{t^{2} + 1} \cdot d t t = (\frac{ρ g x - P}{\sqrt{4 ρ g P_{0} l_{0}}})$

Se descompone en la suma de dos integrales

$\int \sqrt{t^{2} + 1} d t = \int \frac{t^{2} + 1}{\sqrt{t^{2} + 1}} d t = \int \frac{t \cdot t}{\sqrt{t^{2} + 1}} d t + \int \frac{d t}{\sqrt{t^{2} + 1}} = \frac{t \sqrt{t^{2} + 1} + \ln (t + \sqrt{t^{2} + 1})}{2}$

El primer término se integra por partes, y el segundo es una integral inmediata. El resultado final es

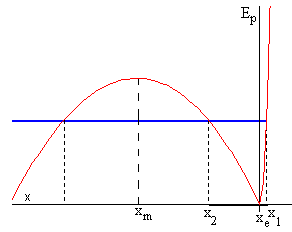
$\begin{array}{l} f (x) = (\frac{x}{2} - \frac{P}{2 ρ g}) \sqrt{{(ρ g x - P)}^{2} + 4 ρ g P_{0} l_{0}} + \\ 2 P_{0} l_{0} \ln (ρ g x - P + \sqrt{{(ρ g x - P)}^{2} + 4 ρ g P_{0} l_{0}}) \end{array}$

Una de las posibles representaciones gráficas de E_p(x) se muestra en la figura.

Para presiones bajas del aire contenido en el recipiente, la función potencial tiene un mínimo local en x_e>0, que es una posición de equilibrio estable, y un máximo local en una posición x_m<0 (equilibrio inestable)
Cuando la presión P se hace igual a la crítica, el máximo y el mínimo coinciden en x=0. Para esta presión y valores superiores de la misma el tubo de ensayo se hunde en el recipiente.

Si en la posición de equilibrio, x_e le damos al tubo una velocidad inicial v₀, la energía total del móvil es la energía cinética ya que la energía potencial es nula.

$E = \frac{1}{2} m v_{0}^{2} = \frac{1}{2} (ρ_{v} V) v_{0}^{2}$

La energía E total es constante en todos los puntos de la trayectoria. Si E es menor que el máximo local de la energía potencial, el tubo que sale de la posición de equilibrio x_e oscila entre dos posiciones, x₁ y x₂ determinadas por las raíces de la ecuación trascendente E_p(x)-E=0, abscisas de los puntos de intersección de la curva de la energía potencial y la recta horizontal E_p(x)=E, tal como se indica en al figura.

Cuando la función energía potencial E_p(x) no tiene mínimo local o posición de equilibrio estable, el tubo sale de la posición x=0 con velocidad v₀ y se hunde en el recipiente hasta que llega al fondo.

Se simula el movimiento del diablillo de Descartes resolviendo numéricamente, la ecuación diferencial del movimiento, con las condiciones iniciales especificadas.

Cálculo con MATLAB

Elegimos el tubo número 2. La representación gráfica de la energía potencial E_p(x) para varios valores de la presión P es

L=16/100; %longitud
l0=7/100; %longitud vacía
d_int=1.43/100; %diámetro interior
d_ext=1.64/100; %diámetro exterior
V=pi*L*(d_ext^2-d_int^2)/4;
A=pi*d_int^2/4;
rho=1000; %densidad agua
rho_g=2.29*1000; %densidad vidrio
P0=1.013e5; %presión atmosférica
hold on
for P=(1:0.02:1.08)*P0
    a=rho^2*9.8*(V/L+A);
    b=rho*P*(V/L+A)-(rho_g-rho)*V*rho*9.8;
    c=-V*rho*P0*l0/L-(rho_g-rho)*V*P;
    z=(-b+sqrt(b^2-4*a*c))/(2*a);
    xe=P0*l0/(P+z*rho*9.8)-z; %equilibrio
    f=@(x) -(P/(2*rho*9.8)-x/2).*sqrt((P-rho*9.8*x).^2+4*rho*9.8*P0*l0)
+2*P0*l0*log(sqrt((P-rho*9.8*x).^2+4*rho*9.8*P0*l0)-(P-rho*9.8*x));
    U1=@(x) rho*9.8*(A/2+V/L)*x.^2/2+(A*P/2+V*(rho_g-rho)*9.8)*x-A*f(x)/2;
    U2=@(x) -A*rho*9.8*x.^2/4+(A*P/2+V*(rho_g-rho)*9.8)*x-A*f(x)/2;
    C1=-U1(xe);
    C2=-U2(xe);
    U=@(x) (U1(x)+C1).*(x>0)+(U2(x)+C2).*(x<=0);
    fplot(U,[-1.2,0.1], 'displayName',num2str(P/P0))
end
hold off
grid on
xlabel('x')
ylim([-0.002,0.004])
legend('-DynamicLegend','location','best')
ylabel('E_p(x)')
title('Energía potencial')

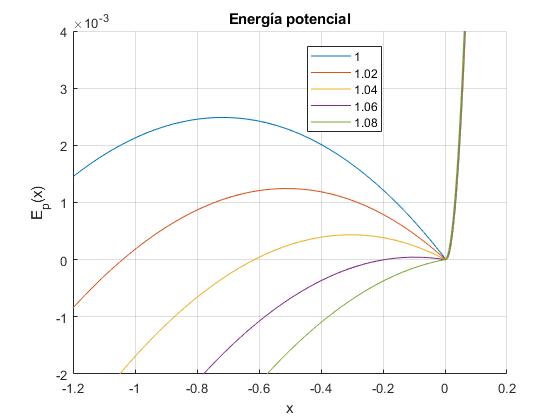
Movimiento del diablillo de energía E entre dos posiciones para una presión P=P₀

L=16/100; %longitud
l0=7/100; %longitud vacía
d_int=1.43/100; %diámetro interior
d_ext=1.64/100; %diámetro exterior
V=pi*L*(d_ext^2-d_int^2)/4;
A=pi*d_int^2/4;
rho=1000; %densidad agua
rho_g=2.29*1000; %densidad vidrio
P0=1.013e5; %presión atmosférica
P=P0; %presión
a=rho^2*9.8*(V/L+A);
b=rho*P*(V/L+A)-(rho_g-rho)*V*rho*9.8;
c=-V*rho*P0*l0/L-(rho_g-rho)*V*P;
z=(-b+sqrt(b^2-4*a*c))/(2*a);
xe=P0*l0/(P+z*rho*9.8)-z; %equilibrio
f=@(x) -(P/(2*rho*9.8)-x/2).*sqrt((P-rho*9.8*x).^2+4*rho*9.8*P0*l0)+
2*P0*l0*log(sqrt((P-rho*9.8*x).^2+4*rho*9.8*P0*l0)-(P-rho*9.8*x));
U1=@(x) rho*9.8*(A/2+V/L)*x.^2/2+(A*P/2+V*(rho_g-rho)*9.8)*x-A*f(x)/2;
U2=@(x) -A*rho*9.8*x.^2/4+(A*P/2+V*(rho_g-rho)*9.8)*x-A*f(x)/2;
C1=-U1(xe);
C2=-U2(xe);
U=@(x) (U1(x)+C1).*(x>0)+(U2(x)+C2).*(x<=0);
fplot(U,[-1.2,0.1])

E=0.002; %energía
ff=@(x) U(x)-E;
line([-1.2,0.1],[E,E],'color','k')
x1=fzero(ff,[xe,0.1]); %posiciones de retorno
x2=fzero(ff,[-0.7,xe]);
line([x1,x1],[0,U(x1)],'color','k','lineStyle','--')
line([x2,x2],[0,U(x2)],'color','k','lineStyle','--')
line([x1,x2],[0,0],'color','r')
ylim([0,0.003])
grid on
xlabel('x')
ylabel('E_p(x)')
title('Energía potencial')

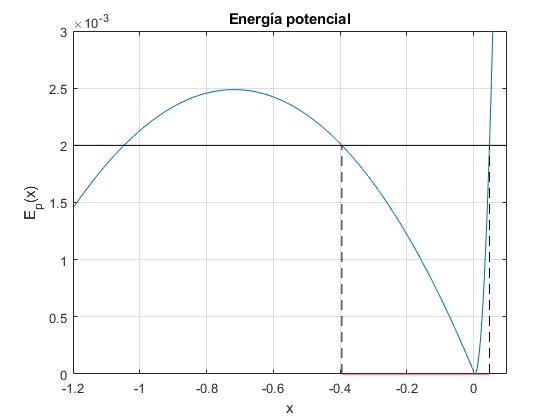
El diablillo de energía E=0.002 se puede mover entre las dos posiciones x₁ y x₂ en los extremos del segmento de color rojo. Estas dos posiciones son las raíces de la ecuación transcendente E_p(x)-E=0 y se obtienen mediante la función fzero de MATLAB

El diablillo de la situación anterior, de masa m, parte de la posición de equilibrio x_e con velocidad $v_{0} = \sqrt{2 E / m}$ . La energía potencial en la posición de equilibrio E_p(x_e)=0 es nula

function ludion_1
    L=16/100; %longitud
    l0=7/100; %longitud vacía
    d_int=1.43/100; %diámetro interior
    d_ext=1.64/100; %diámetro exterior
    V=pi*L*(d_ext^2-d_int^2)/4;
    A=pi*d_int^2/4;
    rho=1000; %densidad agua
    rho_g=2.29*1000; %densidad vidrio
    P0=1.013e5; %presión atmosférica
    P=P0;
    m=18.6/1000; %masa
 
    a=rho^2*9.8*(V/L+A);
    b=rho*P*(V/L+A)-(rho_g-rho)*V*rho*9.8;
    c=-V*rho*P0*l0/L-(rho_g-rho)*V*P;
    z=(-b+sqrt(b^2-4*a*c))/(2*a);
    xe=P0*l0/(P+z*rho*9.8)-z; %equilibrio
    E=0.002; %energía
    v=sqrt(2*E/m); %velocidad
    [t,x]=ode45(@ludion_ode45,[0,10],[xe,-v]);
    plot(t,x(:,1))
    grid on
    xlabel('t')
    ylabel('x')
    title('Movimiento')
   
    function dr=ludion_ode45(~, x)
        a=rho*9.8;
        b=P+abs(x(1))*rho*9.8;
        c=P*x(1)-P0*l0;
        if x(1)<=0
            c=-P0*l0;
        end
        xi=(-b+sqrt(b^2-4*a*c))/(2*a);
        temp=A*xi*rho*9.8+V*(1-x(1)/L)*rho*9.8-V*rho_g*9.8;%-0.01*x(2);
        if x(1)<=0
            temp=A*xi*rho*9.8+V*(rho-rho_g)*9.8;%-0.01*x(2);
        end
        dr=[x(2); temp/m];
    end
end

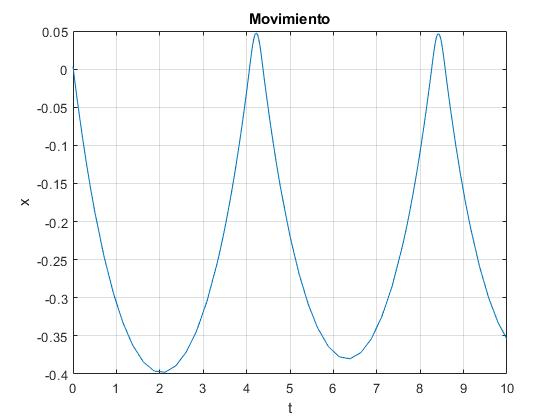
Observamos que el procedimiento ode45 no resuelve bien la ecuación diferencial, debido a los cambios bruscos de velocidad cerca del origen x=0. Sin embargo, el procedimiento de Runge-Kutta empleado en la simulación, más abajo, resuelve bastante bien este sistema conservativo

Añadimos un rozamiento proporcional a la velocidad, λv, debido a las bajas velocidades con las que se mueve el diablillo en el seno del fluido. En la simulación, más abajo, supondremos que no hay rozamiento

function ludion_2
    L=16/100; %longitud
    l0=7/100; %longitud vacía
    d_int=1.43/100; %diámetro interior
    d_ext=1.64/100; %diámetro exterior
    V=pi*L*(d_ext^2-d_int^2)/4;
    A=pi*d_int^2/4;
    rho=1000; %densidad agua
    rho_g=2.29*1000; %densidad vidrio
    P0=1.013e5; %presión atmosférica
    P=P0;
    m=18.6/1000; %masa
 
    a=rho^2*9.8*(V/L+A);
    b=rho*P*(V/L+A)-(rho_g-rho)*V*rho*9.8;
    c=-V*rho*P0*l0/L-(rho_g-rho)*V*P;
    z=(-b+sqrt(b^2-4*a*c))/(2*a);
    xe=P0*l0/(P+z*rho*9.8)-z; %equilibrio
    E=0.002;
    v=sqrt(2*E/m); %velocidad
    [t,x]=ode45(@ludion_ode45,[0,10],[xe,-v]);
    plot(t,x(:,1))

    grid on
    xlabel('t')
    ylabel('x')
    title('Movimiento')
   
    function dr=ludion_ode45(~, x)
        a=rho*9.8;
        b=P+abs(x(1))*rho*9.8;
        c=P*x(1)-P0*l0;
        if x(1)<=0
            c=-P0*l0;
        end
        xi=(-b+sqrt(b^2-4*a*c))/(2*a);
        temp=A*xi*rho*9.8+V*(1-x(1)/L)*rho*9.8-V*rho_g*9.8-0.01*x(2);
        if x(1)<=0
            temp=A*xi*rho*9.8+V*(rho-rho_g)*9.8-0.01*x(2);
        end
        dr=[x(2); temp/m];
    end
end

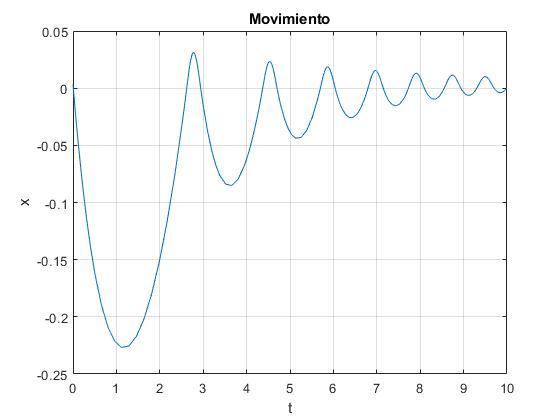
Actividades

Se introduce

El tipo de tubo de ensayo que se va a usar en la experiencia, seleccionándolo en el control de selección titulado Tubos

Se pulsa en el botón titulado Nuevo

Se modifica la altura l₀ inicial de la burbuja de aire en el tubo, moviendo con el puntero del ratón el círculo de color rojo, situada al lado de la imagen amplificada del tubo.
Se modifica la presión ΔP=P-P₀ en mm de mercurio, del aire contenido en el recipiente, actuando en la barra de desplazamiento, o introduciendo su valor en el control titulado Presión.
Se introduce el valor de la velocidad inicial v₀ del tubo en el control titulado Velocidad en la posición inicial x_e de equilibrio estable, si existe. En caso contrario, la posición inicial es x=0,

Se pulsa en el botón titulado ►

Observamos el movimiento del tubo, oscilatorio, si la energía total E del tubo es menor que la del máximo local de la energía potencial. Se representa a la izquierda, la curva E_p(x), la energía total E, y los puntos x₁ y x₂ de retorno.

En el caso de que E sea mayor que el máximo local, el tubo se hunde en el recipiente y llega hasta el fondo. Lo mismo ocurre si la curva de energía potencial no tiene mínimo ni máximo local, es decir, la presión del aire contenido en el recipiente es superior a la crítica.

Si no hay posición de equilibrio estable, modificamos la presión o bien, modificamos el tamaño inicial l₀ de la burbuja de aire actuando con el puntero del ratón en el círculo de color rojo.

Para comenzar una nueva “experiencia” se pulsa en el botón titulado Nuevo. Se utiliza los botones pausa || y paso a paso >| para medir la amplitud de la oscilación y el periodo

Presión (mm Hg)
Velocidad (m/s)
Tubos:

Referencias

Güémez J, Fiolhais C, Fiolhais M. The Cartesian diver and the fold catastrophe. Am. J. Phys. 70 (7) July 2002, pp. 710-714.