Oscilaciones de una boya que flota en el agua
Situación de equilibrio
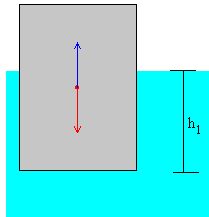
En el equilibrio, la boya estará sumergida una altura h1 dada por el principio de Arquímedes:
peso=empuje
ρsghS=ρfgh1S , es decir,
ρsh=ρfh1
Supongamos que colocamos un bloque de masa m sobre la boya (por ejemplo, una persona que salta sobre la boya).
La nueva posición de equilibrio h2 se deduce del principio de Arquímedes
mg+ρsghS=ρfgh2S
Oscilaciones
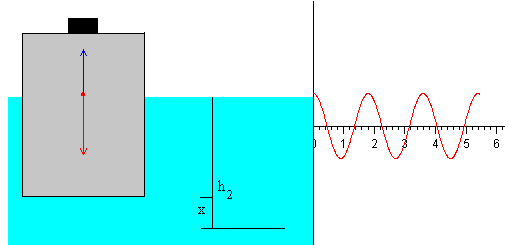
Al colocar el bloque sobre la boya y soltarlo el sistema bloque-boya comienza a oscilar. Hallaremos el periodo de las oscilaciones
Calculamos la fuerza neta que actúa cuando la boya se ha desplazado x de la posición de equilibrio. Como vemos en la figura, si el desplazamiento x es hacia arriba, la resultante es hacia abajo. La fuerza es de signo contrario al desplazamiento.
F=empuje-peso=ρfgS(h2-x)g-(mg+ρsghS)= -ρfSxg
La fuerza es proporcional al desplazamiento y de signo contrario a éste. El sistema describe un M.A.S. cuya frecuencia y periodo hallamos a partir de la segunda ley de Newton
(m+ρshS)a=-ρfSxg
o bien, expresado en forma de ecuación diferencial del MAS
El periodo es, por tanto,
La ecuación del MAS, solución de la ecuación diferencial es
x=A·sin(ωt+φ )
v=Aω cos(ω t+φ )
Las condiciones iniciales determinan la amplitud A y la fase inicial φ .
El bloque se suelta cuando la boya se ha sumergido h1, al poner el bloque, en la nueva posición de equilibrio la boya se sumerge h2.
Luego, en el instante t=0, el desplazamiento de la boya respecto a su nueva posición de equilibrio es x=h2-h1 y su velocidad v=0.
h2-h1=A·sinφ
0=Aω cosφ
La fase inicial es φ =π/2 y la amplitud A= h2-h1
La ecuación del M.A.S. es finalmente,
x=(h2-h1)·sin(ω t+π /2)=(h2-h1)·cos(ω t)
Ejemplo:
Sea, ρs=600 kg/m3, S=0.5 m2, y m=100 kg. La altura de la boya es de 1.0 m, y está fijada en el programa interactivos
La boya se sumerge en el agua hasta la altura
600·1=1000·h1, es decir, h1=0.6 m ó 60 cm
Situamos el bloque de color negro sobre la boya. El sistema boya-bloque empieza a oscilar.
La nueva posición de equilibrio h2 se calcula aplicando de nuevo el principio de Arquímedes
100+600·1·0.5=1000·0.5·h2, es decir, h2=0.8 m ó 80 cm
Medimos esta altura, parando el movimiento, cuando el sistema oscilante pasa por la posición de equilibrio (usar los botones || y >|)
La amplitud de la oscilación es 0.8-0.6 =0.2 m ó 20 cm tal como podemos ver en la representación gráfica posición-tiempo.
El periodo de las oscilaciones es
Medimos el periodo sobre el eje horizontal en la representación gráfica de x en función de t.
Cuando situamos el bloque sobre la boya, el centro de masas deja de estar en el centro de la boya. La nueva posición del c.m. relativo al centro de la boya se calcula mediante la siguiente fórmula
En este ejemplo, xcm=0.125 m, o 12.5 cm por encima del centro de la boya.
El c.m. del sistema boya-bloque oscilará alrededor de la posición 0.8-0.5-0.125=0.175 m ó 17.5 cm por debajo de la superficie del agua.
Actividades
Se introduce
- La densidad de la boya ρs en kg/m3, en el control titulado Densidad
- El área de la base de la boya S en m2, en el control titulado Área.
- La altura h=1 m de la boya está fijada en el programa.
- La masa m del bloque en kg se introduce en el control titulado Masa bloque.
Se pulsa el botón titulado Nuevo y se ve la boya flotando sobre en el agua
Se pulsa el botón titulado ► y el bloque de color negro se coloca encima de la boya que empieza a oscilar. Supondremos que no hay rozamiento y la amplitud de la oscilación se mantiene constante. Se utiliza los botones pausa || y paso a paso >| para medir la amplitud de la oscilación y el periodo
Si los datos introducidos hacen que el sistema bloque-boya quede completamente sumergido durante la oscilación, se pide al usuario para que cambie los datos.

