Medida de la densidad de un líquido y de un sólido

Medida de la densidad un líquido

Conocida la masa del cuerpo y el volumen de la parte sumergida, determinamos la densidad del líquido. En esto se basan los aerómetros o flotadores de masa conocida que se sumergen en el líquido de densidad desconocida. Disponen de una escala graduada, que nos proporcionan mediante lectura directa la densidad del líquido. La superficie libre del líquido marca el valor de la densidad en la escala del aerómetro.

Dependiendo de la aplicación concreta los aerómetros reciben nombres específicos: alcohómetros, sacarímetros, etc.

El aerómetro de la fotografía es un tubo de vidrio, que dispone de un lastre formado por bolitas de plomo (en extremo izquierdo). En la parte derecha, dispone de una escala graduada que mide directamente la densidad del líquido en g/cm³. Laboratorio de Física. Escuela de Ingeniería de Eibar

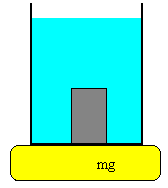
Para un cuerpo en equilibrio que flota sobre la superficie de un líquido, tenemos que el peso es igual al empuje

mg=ρ_fVg

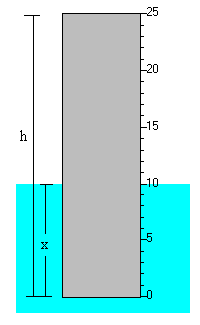
Nuestro aerómetro es un sólido de forma cilíndrica de 25 cm de altura y densidad 0.5 g/cm³ que se sumerge parcialmente en el líquido cuya densidad se quiere determinar.

Midiendo en la escala graduada la parte del cilindro que está sumergida, determinamos la densidad del fluido.

El cuerpo está en equilibrio flotando en el líquido, bajo la acción de dos fuerzas, su peso y el empuje del fluido.

peso=empuje

ρ_sgSh=ρ_f·gSx

ρ_sh=ρ_f x

Donde ρ_s es la densidad del cuerpo sólido, S su sección, h su altura. ρ_f es la densidad del fluido y x la parte del sólido que está sumergido en el líquido.

Ejemplo:

Sea agua el líquido de densidad desconocida

Observamos que el cilindro se sumerge hasta una altura x=12.5 cm

0.5·25=ρ_f 12.5

Se despeja ρ_f =1.0 g/cm³

Actividades

Se selecciona el fluido cuya densidad deseamos conocer en la lista de líquidos: agua, aceite, alcohol, glicerina.
La densidad del sólido se ha fijado en ρ_s=0.5 g/cm³
La altura del cuerpo sólido de forma cilíndrica se ha fijado en h=25 cm

Se pulsa el botón titulado Nuevo.

Se lee en la escala la longitud x del cuerpo cilíndrico que está sumergido y se calcula densidad del líquido ρ_f.

Líquidos:

Medida de la densidad de un sólido

En la página titulada “La balanza. Medida de la densidad de un sólido” se ha estudiado el procedimiento de medida de la densidad de un cuerpo sólido, con una balanza ordinaria:

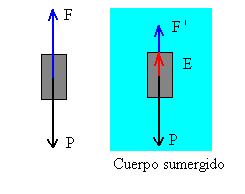
Se pesa el cuerpo sólido y se anota la lectura en gramos m=F de los indicadores de la balanza cuando su brazo está horizontal en equilibrio.
Se sumerge el cuerpo completamente en agua (densidad 1.0 g/cm³) y se anota la lectura F’

La diferencia V=F-F’ es el volumen del cuerpo expresado en cm³.

La densidad es el cociente ρ=m/V (g/cm³)

En esta sección, se mide la densidad ρ>1.0 de un cuerpo sólido por otro procedimiento, empleando una balanza electrónica.

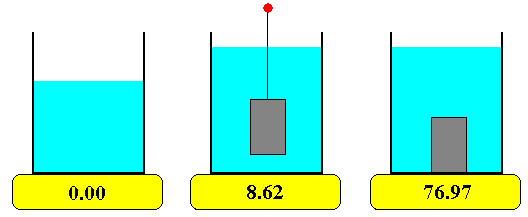
Llenamos un recipiente parcialmente de agua y lo colocamos sobre una balanza electrónica, poniendo a cero el indicador del peso.
Atamos un hilo a un cuerpo sólido, lo sumergimos completamente en agua pero sin tocar el fondo, anotamos la lectura de la balanza V.
Soltamos el cuerpo, dejando de tirar del hilo, de modo que descanse en el fondo del recipiente, anotamos la lectura de la balanza m.

La densidad del cuerpo es el cociente entre la segunda lectura y la primera. ρ=m/V

Cuando un cuerpo está suspendido en el fluido completamente sumergido pero sin tocar el fondo, las fuerzas sobre el cuerpo son:

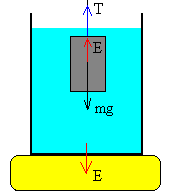
La tensión del hilo T
El peso mg
El empuje E=ρ_f·g·V, siendo ρ_f=1.0 g/cm³ la densidad del líquido (agua)

El cuerpo está en equilibrio, suspendido del hilo T=mg-ρ_f·g·V

El líquido ejerce una fuerza E=ρ_f·g·V sobre el cuerpo cilíndrico, por la tercera ley de Newton, el cuerpo ejerce una fuerza igual y de sentido contrario sobre el líquido

La balanza electrónica mide la fuerza de empuje E₁=ρ_f·g·V

Cuando el cuerpo descansa en el fondo. La balanza electrónica mide el peso del cuerpo F₂=mg=ρV·g

La densidad del sólido ρ es el cociente F₂/E₁, si el líquido es agua ρ_f=1.0 g/cm³

Actividades

Se selecciona el sólido cuya densidad deseamos conocer en la lista de materiales: hierro, oro, plomo, etc...
La densidad del líquido (agua) se ha fijado en ρ_f=1.0 g/cm³
La altura del cuerpo sólido de forma cilíndrica se ha fijado en h=1.0 cm

Se pulsa el botón titulado Nuevo.

Se introduce el sólido en el agua, actuando en el control titulado Posición. Se simula una cuerda que sostiene el bloque cuya densidad es mayor que la del fluido. Cuando llega al fondo, se deja de tirar de la cuerda (desaparece), el bloque descansa en el fondo del recipiente.

Se calcula la densidad del sólido a partir de la lectura de la balanza electrónica:

Cuando el cuerpo está suspendido del hilo en el líquido, completamente sumergido
Cuando el cuerpo descansa en el fondo del recipiente

Nota: cuando se sumerge el sólido, el nivel del líquido en el recipiente debería cambiar. Esto no afecta a la medida de la densidad, que es independiente de la altura del nivel siempre que haya suficiente agua para que el cuerpo se encuentre completamente sumergido.

Posición:
Sólidos:

Medida de la aceleración de la gravedad

Se coloca un vaso cilíndrico de radio R parcialmente lleno de agua sobre una balanza digital y se tara a cero. Situamos el origen en la superficie libre del líquido

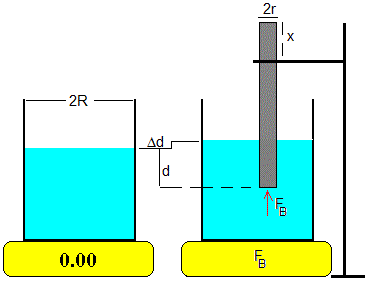
Una varilla metálica de radio r se introduce en el líquido hasta una profundidad d. Como consecuencia, la altura de la superficie libre del líquido se eleva Δd.

$\begin{array}{l} π (R^{2} - r^{2}) Δ d = π r^{2} (d + Δ d) \\ Δ d = \frac{r^{2}}{R^{2} - 2 r^{2}} d \end{array}$

La fuerza F_B que ejerce el líquido sobre el extremo inferior de la varilla debida a la presión hidrostática es

$F_{B} = ρ g (d + Δ d) (π r^{2}) = ρ g V$

Siendo ρ=997.77 kg/m³ la densidad del agua a 22 °C y V el volumen sumergido de la varilla

Por la tercera ley de Newton, la balanza mide una fuerza F_B en gramos.

La fuerza F_B es proporcional al volumen sumergido V, la constante de proporcionalidad es k=ρg

Representamos F_B en Newtons en función de V en cm³ obtenemos la constante k de proporcionalidad mediante ajuste por regresión lineal. Conocida k obtenemos la aceleración de la gravedad g=k/ρ

La balanza mide la fuerza F_B en gramos que se convierte en Newtons dividiendo entre 1000 y multiplicando por la aceleración de la gravedad estándar g₀=9.806 65 m/s². La mayor parte de las balanzas electrónicas miden la fuerza pero muestran la masa. Estan calibradas suponiendo que la aceleración de la gravedad es g₀

El recipiente es un vaso de R=35 mm de diámetro que contiene 400 ml de agua destilada a 22 °C. La varilla es de aluminio de r=5 mm de radio.

En la práctica, es más cómodo medir la distancia x entre el extremo superior de la varilla y la posición de sujección, en vez de la posición del extremo inferior d de la varilla.

Profundidad d (cm)	Fuerza (g)
0.00	0.00
0.38	0.33
1.02	0.81
1.74	1.42
2.52	2.02
3.19	2.56
4.00	3.23
4.83	3.89
5.65	4.49
6.36	5.07
6.89	5.50
7.66	6.13
8.48	6.79

d=[0.00,0.38,1.02,1.74,2.52,3.19,4.00,4.83,5.65,6.36,6.89,7.66,8.48]; %en cm
FB=[0.00,0.33,0.81,1.42,2.02,2.56,3.23,3.89,4.49,5.07,5.50,6.13,6.79]*
9.80665/1000; %en N
r=5; %radio varilla en mm
R=35; %radio recipiente em mm
delta=r^2*d/(R^2-2*r^2); %corrección en cm
V=pi*(d+delta)*r^2/100; %en cm^3
plot(V,FB,'ro','markersize',3,'markerfacecolor','r')
xlabel('V(cm^3)')
ylabel('F_B(N)')
title('Medida de la aceleración de la gravedad')
grid on

En el menú, seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en TYPES OF FIT.

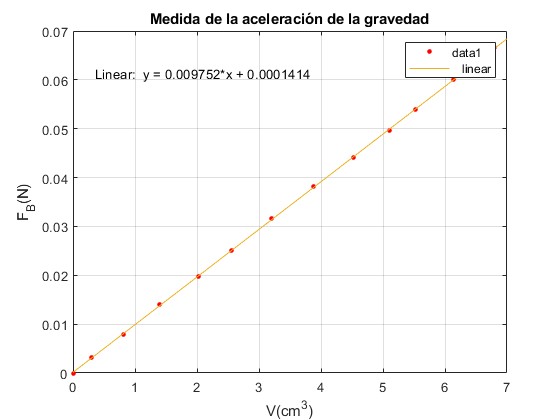
La pendiente de la recta que mejor ajusta es k=0.009752 N/cm³. La aceleración local de la gravedad es

$g = \frac{k}{ρ} = \frac{0.009752 \cdot 10^{6}}{997 .77} = 9 .7738 \frac{m}{s^{2}}$

Actividades

Se introduce

La profundidad d, en el control titulado d mm

Se pulsa el botón titulado Nuevo

En la balanza representada por el rectágulo de color amarillo, aparece la fuerza F_B en gramos

En la parte superior, se proporciona al dato de la corrección Δd en mm que es pequeña, comparada con la profundidad d

d (mm):

Referencias

Medida de la densidad de un sólido

Ellis D. Noll. Confronting the Bouyant Force. The Physics Teacher, Vol 40, January 2002, pp. 8-10

Medida de la aceleración de la gravedad

Ivica Aviani, Nataša Erceg. Measuring g using buoyancy: a simple and accurate method for high-school physics lab. Phys. Educ. 60 (2025) 055015