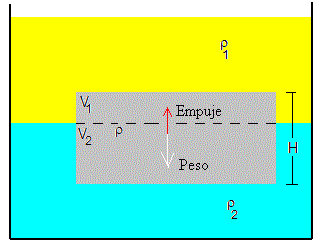
Supongamos un cuerpo de densidad ρ (hielo) que flota entre dos fluidos de densidades ρ₁ (aire) y ρ₂ (agua), tal que ρ₁<ρ<ρ₂

Aplicamos el principio de Arquímedes: peso es igual al empuje

${\displaystyle \begin{array}{l}\{\begin{array}{l}\rho gV={\rho }_{1}g{V}_1+{\rho }_{2}g{V}_2\\ V=V_1+V_2\end{array}\\ V_1=\frac{{\rho }_2-\rho }{{\rho }_2-{\rho }_1}V,V_2=\frac{\rho -{\rho }_1}{{\rho }_2-{\rho }_1}V\end{array}}$

V₁ es el volumen de hielo en el aire y V₂ es el volumen de hielo sumergido en el agua

Al cabo de cierto tiempo, el hielo se funde en el vaso de agua. La masa de hielo ρV se convierte en agua ρ₂V'. En el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}\rho V={\rho }_1{V}_1+{\rho }_2{V}_2\\ \rho V={\rho }_{2}V\text{'}\end{array}\\ V\text{'}=V_2+\frac{{\rho }_1}{{\rho }_2}{V}_1\\ \Delta V=\frac{{\rho }_1}{{\rho }_2}{V}_1=\frac{{\rho }_1}{{\rho }_2}\frac{{\rho }_2-\rho }{{\rho }_2-{\rho }_1}V\end{array}}$

Vemos que V'>V₂, el volumen de hielo sumergido en agua. Cuando se funde el hielo, el nivel de agua se eleva. Vamos a estimar cuando se eleva.

Sea A_c el área de la sección del recipiente cilíndrico, y sea A_h el área de la sección del hielo y H su altura, supuesto también de forma cilíndrica.

• Supongamos que A_c≈A_h
• Densidad del hielo, ρ=917 kg/m³
• Densidad del agua, ρ₂=1000 kg/m³
• Densidad del aire, ρ₁=1.29 kg/m³

El resultado es h=1.0721·10^-4H. El factor tan pequeño se debe a que la densidad del aire es mucho menor que la del agua, ≈1/1000

Si H=2 cm=20 mm, h=0.0021 mm. Imposible de apreciar

Efectos térmicos

Cuando se funde el hielo, cambia la temperatura del agua

Consideremos una mezcla de m=ρV de hielo a la temperatura de 0°C con una masa m₂ de agua a la temperatura t₀. La temperatura final es t_f.

• EL calor cedido por el agua para pasar de la temperatura t₀ a otra inferior t_f es, m₂c₂(t₀-t_f)

• El calor absorbido por la masa m de hielo es m·L_f para fundir el hielo y mc₂t_f para elevar su temperatura

Despejamos la temperatura final de equilibrio t_f

${\displaystyle \begin{array}{l}{m}_2{c}_2\left(t_0-t_f\right)=m{L}_f+m{c}_2{t}_f\\ t_f=\frac{m_2{c}_2{t}_0-m{L}_f}{c_2\left(m_2+m\right)}\end{array}}$

Donde c₂=4186 kg/(kg·K) es el calor específico del agua, y L_f=334 000 J/kg es el calor de fusión

El cambio total de volumen es ΔV_t=ΔV+ΔV_q

${\displaystyle \begin{array}{l}\Delta V_t=\frac{{\rho }_1}{{\rho }_2}\frac{{\rho }_2-\rho }{{\rho }_2-{\rho }_1}V+\Delta V_q\\ \Delta V_q={\displaystyle \underset{T_0}{\overset{T_f}{\int }}k(T)V·dT}\approx <k>V_2\left(T_f-T_0\right)\end{array}}$

Donde k(T) es el coeficiente de dilatación térmica que cambia con la temperatura. Podemos tomar su valor medio <k> para un intervalo pequeño de temperaturas, V₂ es el volumen inicial de agua

Quedaría por demostrar si el segundo término ΔV_q (negativo) es mayor (en valor absoluto) menor o igual que el primer término ΔV

Ejemplo

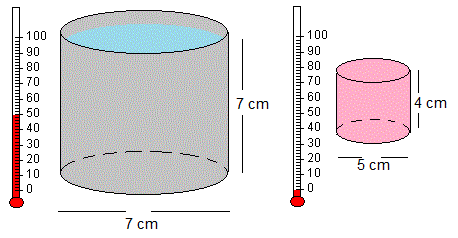
En un vaso de forma cilíndrica de diámetro interno de 7 cm, la altura de agua a 50 °C es de 7 cm, se le echa un trozo de hielo de forma cilíndrica de 5 cm diámetro y 4 cm de altura a 0 °C. La temperatura de la mezcla es

${\displaystyle \begin{array}{l}{V}_2=\pi ·{0.035}^2·0.07\\ V=\pi ·{0.025}^2·0.04\\ m_2=1000·V_2\\ m=715·V\\ t_f=\frac{m_{2}4186·50-m·334000}{4186\left(m_2+m\right)}=22.6\text{ºC}\end{array}}$

El coeficiente de dilatación térmica medio entre las temperaturas 22 y 50 °C es <k>=3.3·10^-4 K^-1, véase la tabla más abajo

${\displaystyle \begin{array}{l}\Delta V_t=\frac{1.29}{1000}\frac{1000-917}{1000-1.29}\left(\pi ·{0.025}^2·0.04\right)+3.3·{10}^{-4}\left(\pi ·{0.035}^2·0.07\right)\left(22.6-50\right)\\ \Delta V_t=8.42·{10}^{-9}-2.43·{10}^{-6}=-2.43·{10}^{-6}{\text{m}}^{\text{3}}=-2.43{\text{cm}}^{\text{3}}\end{array}}$

El volumen de la mezcla (agua+hielo) se contrae si se tienen en cuenta los efectos térmicos, tal como se argumenta en el segundo artículo citado en las referencias

Densidad y coeficiente de dilatación térmica del agua

Fuente: Water - Density, Specific Weight and Thermal Expansion Coefficients. The Engineering ToolBox

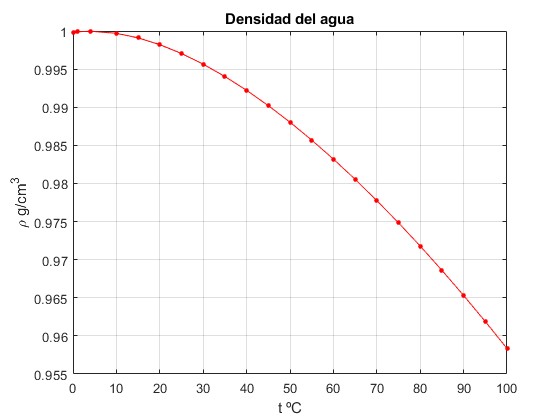
La densidad del agua a 0.1 ºC es de 999.85 kg/m³ alcanza un máximo a una temperatura próxima a 4ºC y luego, disminuye con el incremento de la temperatura (comportamiento normal). El coeficiente de dilatación del agua es por tanto, negativo en el intervalo entre 0 ºC y 4 ºC, y positivo a partir de dicha temperatura.

t=[0.01,1,4,10:5:100];
rho=[999.85,999.90,999.97,999.70,999.10,998.21,997.05,995.65,994.03,992.22,990.21,
988.04,985.69,983.20,980.55,977.76,974.84,971.79,968.61,965.31,961.89,958.35];
plot(t,rho/1000,'-ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('t ºC')
ylabel('\rho g/cm^3')
title('Densidad del agua')

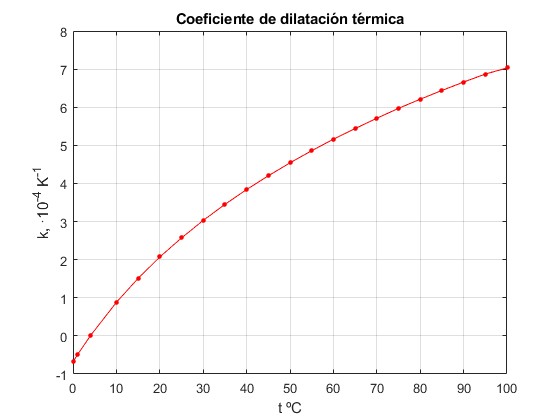
t=[0.01,1,4,10:5:100];
k=[-0.68,-0.50,0.003,0.88,1.51,2.07,2.57,3.03,3.45,3.84,4.20,4.54,
4.86,5.16,5.44,5.71,5.97,6.21,6.44,6.66,6.87,7.03];
plot(t,k,'-ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('t ºC')
ylabel('k, ·10^{-4} K^{-1}')
title('Coeficiente de dilatación térmica')

Referencias

Boon Leong Lan. An ice-cube puzzle. Phys. Educ. 36 2001, pp. 75-76

F M S Lima, F F Monteiro. Thermal effects on the ‘ice-cube puzzle’. Eur. J. Phys. 33 (2012) pp. 439–442