Un recipiente abierto por arriba lleno de agua se sitúa sobre una placa eléctrica, se espera un tiempo hasta que se establece el estado estacionario, la temperatura del agua en distintos puntos no cambia con el tiempo.

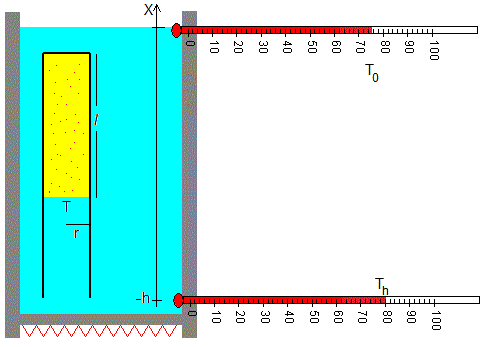
Supongamos que se establece un gradiente de temperaturas con la profundidad tal que la temperatura del fondo x=-h es T_h y la temperatura de la superficie libre x=0 es T₀. La temperatura del agua a una profundidad x es

${\displaystyle T_w(x)=T_0-\frac{T_h-T_0}{h}x}$

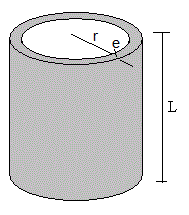
El diablillo o ludión es un tubo de ensayo hecho de vidrio de densidad ρ_v, de longitud L, de sección A=πr², siendo el radio interior r y de espesor e. Su masa es.

${\displaystyle m={\rho }_v\pi \left({\left(r+e\right)}^2-r^2\right)L}$

Despreciamos la masa de la base del tubo.

El tubo se invierte y se introduce en el recipiente. El tubo deberá contener una burbuja de aire de longitud l₀ a la temperatura ambiente T_a. El número de moles n_a de aire seco es,

${\displaystyle p_0\left(A{l}_0\right)=n_{a}R{T}_a}$

Donde p₀=1.013·10⁵ Pa es la presión atmosférica, R es la constante de los gases

La fuerza de empuje

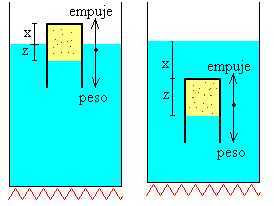
Las fuerzas que actúan sobre el tubo son el peso y el empuje, pero este último no admite una expresión única y es distinta

• Cuando el tubo está parcialmente sumergido, x>0
• Cuando el tubo está completamente sumergido, x≤0

Analizaremos cada uno de los casos por separado

• El empuje del tubo de vidrio que está parcialmente sumergido una longitud L-x.

ρ·g·V(1-x/L)

• El empuje de la burbuja de aire que ha desalojado el agua contenida en el volumen cilíndrico de área A (el área de la sección transversal del tubo) y de altura z.

ρ·g·A·z

La resultante es la diferencia entre el empuje y el peso

${\displaystyle F=\rho gAz+\rho gV\left(1-\frac{x}{L}\right)-{\rho }_{v}gV}$

En el segundo caso, figura de la derecha

• El empuje del tubo de vidrio que ahora está completamente sumergido

ρ·g·V

• El empuje de la burbuja de aire que ha desalojado el agua contenida en el volumen cilíndrico de área A (el área de la sección trasversal del tubo) y de altura z.

ρ·g·A·z

La resultante de las fuerzas que actúan sobre el tubo es la diferencia entre el empuje y el peso

${\displaystyle F=\rho gAz+\rho gV-{\rho }_{v}gV}$

La presión de vapor saturado

La burbuja en el tubo de ensayo, véase la primera figura, contiene una mezcla de aire y vapor saturado cuando la superficie del agua en el tubo de ensayo está una temperatura T

La presión p de la mezcla de aire y de vapor en el volumen Al de la burbuja es la suma de las presiones parciales p=p_a+p_v. Siendo

• p, es la suma de la presión atmosférica p₀ y la presión hidrostática
• p_a, es la presión parcial del aire, supuesto gas ideal, p_a(Al)=n_aRT

• p_v, es la presión de vapor saturado dado por la ecuación de Antoine

${\displaystyle p_v(T)=1000·\exp \left(16.573-\frac{3988.842}{T-39.47}\right)}$

Así pues, las presiones parciales de los componentes de la mezcla, aire y vapor saturado obedecen a leyes distintas. En el caso del aire

${\displaystyle \begin{array}{l}Al=\frac{n_a}{p_a}RT=\frac{\frac{p_{0}A{l}_0}{R{T}_a}}{p-p_v}RT\\ l=\frac{T}{T_a}\frac{p_0}{p-p_v}{l}_0\end{array}}$

Esta es la longitud l de la burbuja, cuando la temperatura de la superficie del agua en el interior del tubo de ensayo es T

Conducción del calor a través de las paredes del tubo de ensayo

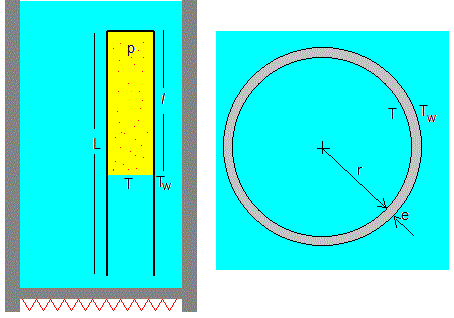
La temperatura de la superficie cilíndrica interior del tubo de ensayo es T, pero la temperatura de la superficie cilíndrica exterior en contacto con el agua del recipiente en la posición de dicho tubo es T_w. Habrá un fujo de calor a través de la superficie lateral del tubo de ensayo de forma cilíndrica de pequeño espesor e y hecho de un material de conductividad térmica K

La cantidad de calor que fluye entre el tubo de ensayo hacia o desde el agua que la rodea, por unidad de área y de tiempo es proporcional al gradiente de temperatura

${\displaystyle J=K\frac{dT}{dx}\approx K\frac{T_w-T}{e}}$

El calor que atraviesa el área lateral del cilindro 2πr(L-l) se emplea en cambiar la temperatura de la masa de agua del tubo de ensayo por debajo de la burbuja de aire y vapor. c es el calor específico del agua

${\displaystyle \begin{array}{l}\rho \left(\pi r^2(L-l)\right)c\frac{dT}{dt}\approx \left(2\pi r(L-l)\right)\left(K\frac{T_w-T}{e}\right)\\ \frac{dT}{dt}=\frac{K}{\rho c}\frac{2}{re}\left(T_w-T\right)\\ \frac{dT}{dt}=k\left(T_w-T\right)\end{array}}$

Ecuaciones del movimiento

• Cuando el tubo de ensayo está parcialmente sumergido, x>0



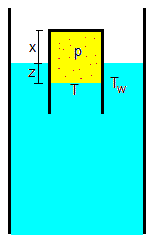
Aplicamos la segunda ley de Newton

${\displaystyle {\rho }_{v}V\frac{d^{2}x}{d{t}^2}=\rho gAz+\rho gV\left(1-\frac{x}{L}\right)-{\rho }_{v}gV}$

La relación entre z y la posición x del tubo es

${\displaystyle \begin{array}{l}x+z=\frac{T}{T_a}\frac{p_0{l}_0}{p-p_v(T)}\\ p=p_0+\rho gz\\ \rho g{z}^2+\left(\rho gx+p_0-p_v(T)\right)z+p_{0}x-p_v(T)x-\frac{T}{T_a}{p}_0{l}_0=0\end{array}}$

La presión p es la suma de la presión atmosférica p₀ y la hidrostática ρgz. Donde z es la raíz positiva de la ecuación de segundo grado

La temperatura T de la superficie del agua en el interior del tubo de ensayo es

${\displaystyle \begin{array}{l}\frac{dT}{dt}=k\left(T_w-T\right)\\ T_w=T_0+\frac{T_h-T_0}{h}z\end{array}}$

T_w es la temperatura del agua del recipiente en la posición z de la superficie del agua en el interior del tubo

• Cuando el tubo de ensayo está completamente sumergido, x≤0



${\displaystyle {\rho }_{v}V\frac{d^{2}x}{d{t}^2}=\rho gAz+\rho gV-{\rho }_{v}gV}$

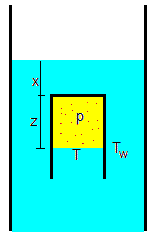
La relación entre z y la posición x del tubo es

${\displaystyle \begin{array}{l}z=\frac{T}{T_a}\frac{p_0{l}_0}{p-p_v(T)}\\ p=p_0+\rho g(\left|x\right|+z)=p_0+\rho g(-x+z)\\ \rho g{z}^2+\left(p_0-\rho gx-p_v(T)\right)z-\frac{T}{T_a}{p}_0{l}_0=0\end{array}}$

La presión p es la suma de la presión atmosférica p₀ y la hidrostática ρg(z+|x|)=ρg(z-x). Donde z es la raíz positiva de la ecuación de segundo grado

La temperatura T de la superficie del agua en el interior del tubo de ensayo es

${\displaystyle \begin{array}{l}\frac{dT}{dt}=k\left(T_w-T\right)\\ T_w=T_0+\frac{T_h-T_0}{h}(-x+z)\end{array}}$

T_w es la temperatura del agua del recipiente en la posición x-z de la superficie del agua en el interior del tubo

Se resuelve el sistema de dos ecuaciones diferenciales para x>0 y para x≤0 por el procedimiento de Runge-Kutta con las siguientes condiciones iniciales. El tubo de ensayo parte de la posición x₀<0, en reposo, dx/dt=0 en el instante t=0. La temperatura inicial T de la superficie del agua en el interior del tubo de ensayo es la temperatura T_w del agua del recipiente a esa profundidad x₀

Cuando el tubo de ensayo se mueve por encima de la superficie del recipiente x>0, se requiere un especial atención. La posición z de la superficie de agua en el interior del tubo de ensayo no puede ser negativa. El programa interactivo se detiene cuando z≤0, e invita al usuario a introducir nuevos valores para los parámetros, de modo que la oscilación se mantenga en el tiempo entre los límites permitidos

El diablillo de Descartes como motor térmico

En este proceso, observaremos que el diablillo toma una energía en forma de calor del agua del recipiente y lo transforma en energía cinética y potencial, incrementando la amplitud de las oscilaciones. Se trata de un sistema no conservativo

Por el contrario, el estudiado en la página titulada El ludión o diablillo de Descartes es un sistema conservativo, la amplitud de las oscilaciones se mantiene constante

Actividades

Se introduce

• La longitud inicial l₀ de la burbuja de aire en el tubo de ensayo a la temperatura ambiente 25 °C, en el control titulado Longitud. Se deberá establecer un valor que haga que el tubo de ensayo ascienda lo más lentamente posible hacia arriba

• La posición inicial del tubo de ensayo en el recipiente, en el control titulado Profundidad

• El gradiente de temperaturas en el recipiente: la temperatura T₀ en la posición x=0, y la temperatura T_h en la posición x=-25 cm, en los controles titulados Temperaturas

• Las dimensiones del tubo de ensayo han sido fijadas en el programa: longitud L=16 cm, radio interior r=0.715 cm, espesor e=0.105 cm, densidad del vidrio, ρ_v=2290 kg/m³. Otros parámetros que se han fijado son, la densidad del agua ρ_w=1000 kg/m³, calor específico, c_w=4186 J/(kg·K), presión atmosférica p₀=1.013·10⁵ Pa

• Se puede elegir la conductividad térmica de las paredes del tubo de ensayo y observar su efecto sobre el movimiento del diablillo

Material	Conductividad térmica W/(m·K)
Conductor	389.6
Aislante	0.74

El cobre es un buen conductor del calor y el vidrio es casi aislante

Es conveniente, conocer el comportamiento del diablillo, en una primera aproximación, suponiendo que el vapor de agua saturado no afecta a su movimiento, para ello se activa el botón de radio titulado Sin vapor saturado. Veremos que la amplitud de la oscilación se mantiene constante

Después, activa el botón titulado Con vapor, para ver el efecto del gradiente térmico establecido en el recipiente sobre el movimiento del diablillo. Se aconseja invertir el gradiente de temperaturas y comparar el efecto sobre el diablillo

En la parte superior derecha, se proporcionan los datos de

• El tiempo t en segundos
• La posición x del tubo de ensayo, del extremo superior del tubo, en cm
• La velocidad dx/dt del tubo de ensayo en cm/s
• La temperatura T en °C de la superficie del agua en el interior del tubo de ensayo, que es la que determina la presión de vapor saturado

Activando la casilla titulada Gráfica después de haber pulsado el botón titulado Nuevo, se representa la posición x del tubo de ensayo en función del tiempo t. Se puede medir el periodo y la amplitud de la oscilación

Referencias

Igor V Grebenev, Olga V Lebedeva, Svetlana V Polushkina. Vapor Cartesian diver. Phys. Educ. 53 (2018) 045023