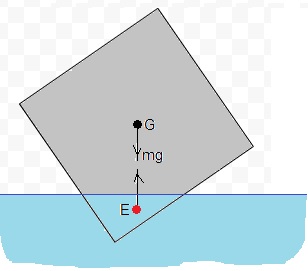
Cuando un cuerpo flota en equilibrio el peso y la fuerza de empuje tienen el mismo valor, la misma dirección pero sentidos contrarios. El punto de aplicación de la primera es el centro de masa G y de la segunda el centro de empuje E.

Sea G la posición del centro de masas del cuerpo y E el centro de masas de la parte sumergida (centro de empuje) y C el centro de masas de la parte expuesta al aire. El punto G está en la línea que une E y C. Sea V el volumen de la parte sumergida y V' de la parte no sumergida. El principio de Arquímedes, peso=empuje se expresa

ρ_s(V+V')=ρV. ρ_s es la densidad del cuerpo y ρ la densidad del agua, el cociente es la densidad relativa q=ρ_s/ρ

q(V+V')=V. Esta ecuación la escribimos de la forma

qV'=(1-q)V

Intercambiando q por (1-q) equivale a intercambiar V por V'

Para la configuración de equilibrio q hay otra configuración imagen 1-q tal como se muestra en la figura

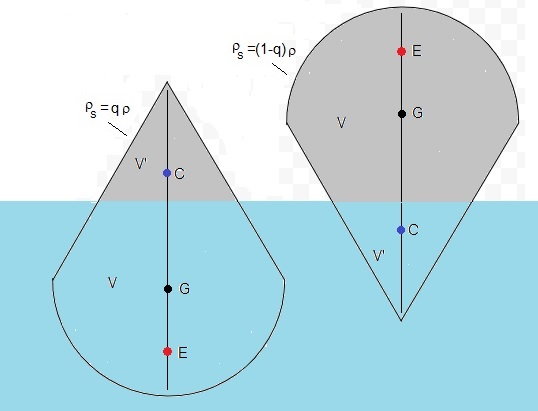
Dos esquinas sumergidas

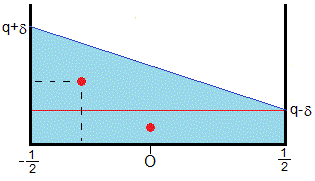
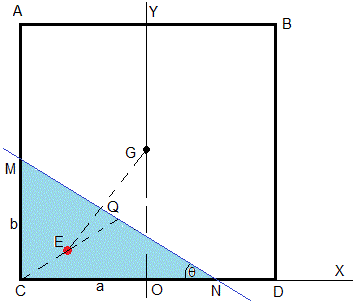
En la figura, se muestra una posible configuración de la sección cuadrada de la barra de lado unidad, con dos de sus esquinas sumergidas

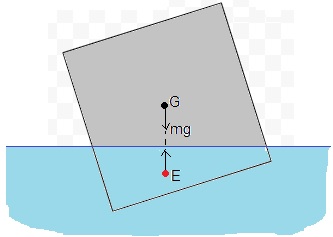
Giramos la figura un ángulo θ y establecemos un sistema de referencia tal como se aprecia en la figura

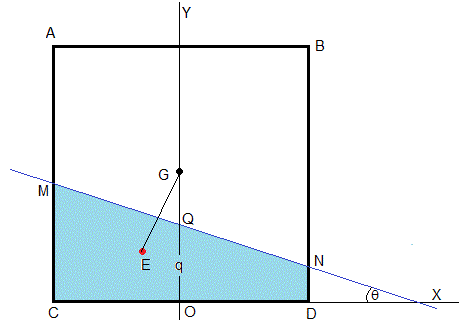
Las coordenadas de las cuatro esquinas ABCD del cuadrado son A(-1/2,1), B(1/2,1), C(-1/2,0), D(1/2,0).

El centro de masa de la sección de la barra se encuentra en el punto G(0,1/2).

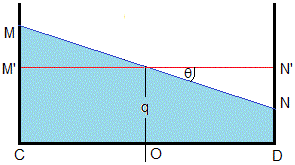
El área del trapecio MNCD es la misma que el área del rectángulo M'N'CD. Como el lado CD=1, la altura del rectángulo es q, la densidad relativa

Llamamos δ=tanθ/2 a la distancia MM' o NN'

Para que las dos esquinas estén sumergidas δ<q. La solución simétrica con δ<0 es tambien posible

Las coordenadas del punto Q(0,q), las de M(-1/2,q+δ), N(1/2,q-δ).

Calculamos las coordenadas del centro de empuje E. Primero, calculamos el centro de masa de una placa triangular de lados a y b

${\displaystyle x_c=\frac{{\displaystyle \underset{0}{\overset{a}{\int }}x\left(y·dx\right)}}{{\displaystyle \underset{0}{\overset{a}{\int }}y·dx}},y_c=\frac{{\displaystyle \underset{0}{\overset{b}{\int }}y\left(x·dy\right)}}{{\displaystyle \underset{0}{\overset{b}{\int }}x·dy}}}$

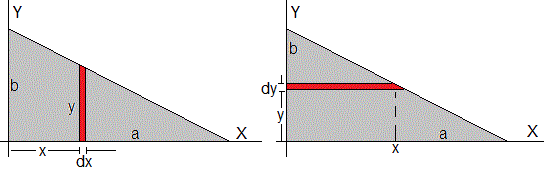
Para integrar precisamos de la relación entre x e y, y=-bx/a+b.

${\displaystyle \begin{array}{l}{x}_c=\frac{{\displaystyle \underset{0}{\overset{a}{\int }}x\left(-\frac{b}{a}x+b\right)dx}}{{\displaystyle \underset{0}{\overset{a}{\int }}\left(-\frac{b}{a}x+b\right)dx}}=\frac{{-\frac{b}{a}\frac{x^3}{3}+b\frac{x^2}{2}|}_0^a}{{-\frac{b}{a}\frac{x^2}{2}+bx|}_0^a}=\frac{\frac{1}{6}b{a}^2}{\frac{1}{2}ba}=\frac{1}{3}a\\ y_c=\frac{{\displaystyle \underset{0}{\overset{b}{\int }}y\left(\frac{a(b-y)}{b}\right)dy}}{{\displaystyle \underset{0}{\overset{b}{\int }}\left(\frac{a(b-y)}{b}\right)dy}}=\frac{{\frac{a}{b}\left(b\frac{y^2}{2}-\frac{y^3}{3}\right)|}_0^b}{{-\frac{b}{a}\frac{x^2}{2}+bx|}_0^a}=\frac{\frac{1}{6}{b}^{2}a}{\frac{1}{2}ba}=\frac{1}{3}b\end{array}}$

El centro de masas del trapecio CMDN, es la suma de un rectángulo de área (q-δ) y centro de masas (0, (q-δ)/2) y de un triángulo rectángulo de área δ y centro de masas (-1/6, (q-δ)+2δ/3)=(-1/6,q-δ/3)

El centro de masas del trapecio o las coordenadas del centro de empuje E son

${\displaystyle x_c=\frac{\left(q-\delta \right)0+\delta \left(-\frac{1}{6}\right)}{\left(q-\delta \right)+\delta }=-\frac{\delta }{6q}}$

${\displaystyle y_c=\frac{\left(q-\delta \right)\left(\frac{q-\delta }{2}\right)+\delta \left(q-\frac{\delta }{3}\right)}{\left(q-\delta \right)+\delta }=\frac{3q^2+{\delta }^2}{6q}}$

Equilibrio

La recta que pasa por el centro de masa G y por el centro de empuje E es perpendicular a la superficie del agua, es decir a la recta MN. En términos de vectores el producto escalar

${\displaystyle \begin{array}{l}\overrightarrow{EG}·\overrightarrow{MN}=0\\ \left\{\left(0-\left(-\frac{\delta }{6q}\right)\right)\widehat{i}+\left(\frac{1}{2}-\frac{3q^2+{\delta }^2}{6q}\right)\widehat{j}\right\}·\left\{\left(\frac{1}{2}-\frac{-1}{2}\right)\widehat{i}+\left((q-\delta )-(q+\delta )\right)\widehat{j}\right\}=0\\ \left\{\frac{\delta }{6q}\widehat{i}+\left(\frac{1}{2}-\frac{3q^2+{\delta }^2}{6q}\right)\widehat{j}\right\}·\left\{\widehat{i}-2\delta \widehat{j}\right\}=\frac{\delta }{6q}-2\delta \left(\frac{1}{2}-\frac{3q^2+{\delta }^2}{6q}\right)=0\\ \frac{\delta }{6q}\left(1-6q+6q^2+2{\delta }^2\right)=\mathrm{0,}\{\begin{array}{l}\delta =0\\ {\delta }^2=3q-3q^2-\frac{1}{2}\end{array}\end{array}}$

El miembro de la derecha es positivo para q>q₁, donde q₁ es la raíz de le ecuación de segundo grado 3q-3q²-1/2=0

${\displaystyle q_1=\frac{3\pm \sqrt{3}}{6}=\{\begin{array}{l}0.7887\\ 0.2113\end{array}}$

Solamente estudiamos las configuraciones de equilibrio para q<0.5, la única raíz posible es q₁=0.2113

Tenemos las primeras configuraciones, δ=0, para q<q₁ y

${\displaystyle \delta =\sqrt{3q-3q^2-\frac{1}{2}}}$

para q>q₁. Por otra parte, δ<q y esto sucede para q<0.25

${\displaystyle 3q-3q^2-\frac{1}{2}=q^2,\{\begin{array}{l}0.5\\ 0.25\end{array}}$

hold on
f=@(x) 3*x-3*x.^2-1/2;
fplot(f, [0,0.5])
q1=(3-sqrt(3))/6;
line([q1,q1],[0,-0.5],'lineStyle','--','color','k')
line([0.25,0.25],[-0.5,sqrt(f(0.25))],'lineStyle','--','color','k')
fplot(@(x) sqrt(f(x)),[q1,0.5])
fplot(@(x) x,[q1,0.5])
hold off
xlabel('q')
ylabel('f(q)')
grid on
title('Función')

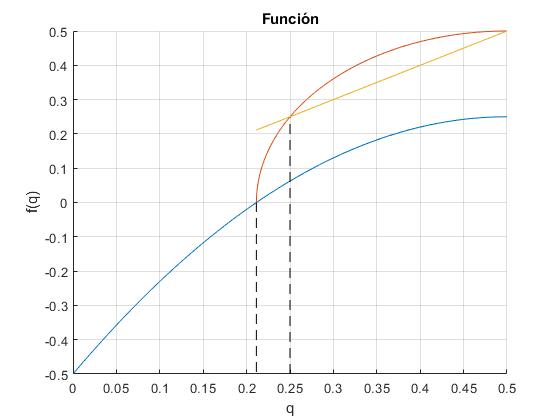
En color azul, se representa la función f(q)=3q-3q²-1/2, que es positiva para q>q₁=0.2113. La curva de color rojo representa δ (la raiz cuadrada de f(q)) en función de q. La recta de color amarillo es δ=q. Como apreciamos, δ<q hasta q=0.25

Resumiendo. Las posibles valores para δ y por tanto, de θ son

${\displaystyle \delta \{\begin{array}{l}\mathrm{0,}0<q<q_1\\ \mathrm{0,}\sqrt{3q-3q^2-\frac{1}{2}},q_1<q<0.25\\ \mathrm{0,}0.25<q<0.5\end{array}}$

En el intervalo q₁<q<0.25 hay dos posibles soluciones, que distinguiremos utilizando el criterio de estabilidad.

Establidad

El criterio de estabilidad es que la distancia EG entre el centro de masa G y el centro de empuje E deberá ser mínima.

Antes hemos calculado el vector $\overrightarrow{EG}$ , el cuadrado de su módulo es

${\displaystyle d^2={\left(\frac{\delta }{6q}\right)}^2+{\left(\frac{1}{2}-\frac{3q^2+{\delta }^2}{6q}\right)}^2}$

La derivada de d² respecto del ángulo θ o respecto de δ=tanθ/2 es

${\displaystyle \begin{array}{l}\frac{d}{d\delta }{d}^2=\frac{2\delta }{{\left(6q\right)}^2}-2\frac{2\delta }{6q}\left(\frac{1}{2}-\frac{3q^2+{\delta }^2}{6q}\right)=0\\ \frac{2\delta }{{\left(6q\right)}^2}-2\frac{2\delta }{6q}\left(\frac{1}{2}-\frac{3q^2+{\delta }^2}{6q}\right)=0\\ \frac{2\delta }{{\left(6q\right)}^2}\left(1-6q+6q^2+2{\delta }^2\right)=0\end{array}}$

Que es el mismo resultado que hemos obtenido anteriormente. Calculamos la derivada segunda

${\displaystyle \frac{d^2}{d{\delta }^2}{d}^2=\frac{2}{{\left(6q\right)}^2}\left(1-6q+6q^2+2{\delta }^2\right)+\frac{2\delta }{{\left(6q\right)}^2}4\delta =\frac{2}{{\left(6q\right)}^2}\left(1-6q+6q^2+6{\delta }^2\right)}$

Signos de la derivada segunda

Representamos la derivada segunda en función de q para valores δ

• δ=0, en color azul

• $\delta =\sqrt{3q-3q^2-\frac{1}{2}}$, en color rosado

hold on
q=linspace(0,0.5,100);
delta=0;
y=2*(1-6*q+6*q.^2+6*delta^2)./(6*q).^2;
plot(q,y)
delta=sqrt(3*q-3*q.^2-1/2);
y=2*(1-6*q+6*q.^2+6*delta.^2)./(6*q).^2;
plot(q,y)
q1=(3-sqrt(3))/6;
line([q1,q1],[-5,5],'lineStyle','--','color','k')
line([0.25,0.25],[-5,5],'lineStyle','--','color','k')
hold off
xlabel('q')
ylim([-5,5])
legend('\delta=0','\delta!=0', 'location', 'best')
ylabel('f''(q)')
grid on
title('Estabilidad')

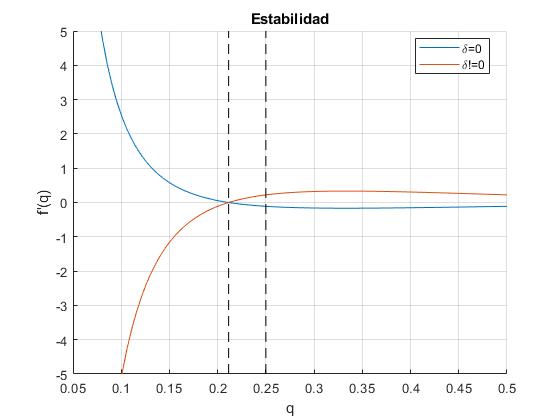
La derivada segunda es positiva (mínimo), equilibrio estable

${\displaystyle \begin{array}{l}\delta =\mathrm{0,}0<q\le q_1\\ \delta =\sqrt{3q-3q^2-\frac{1}{2}},q_1<q\le 0.25\end{array}}$

En el intervalo, 0.25<q<0.5, la solución δ=0, es inestable, la derivada segunda es negativa

Para q=0.25, δ=0.25, y tanθ=1/2

Una esquina sumergida

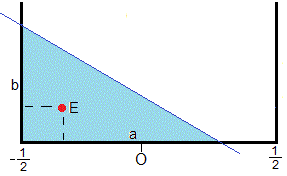
En la figura, se muestra una posible configuración de la sección cuadrada de la barra de lado unidad, con una de sus esquinas sumergida

Giramos la figura un ángulo θ y establecemos un sistema de referencia tal como se aprecia en la figura

El área del triángulo rectángulo MNC es ab/2=q, por otra parte, tanθ=b/a. Despejamos a y b

${\displaystyle a^2=\frac{2q}{\tan \theta },b^2=2q\tan \theta }$

Las coordenadas del centro de empuje E son (-1/2+a/3, b/3). Las coordenadas del centro de masa G son (0,1/2).

Equilibrio

La línea que pasa por el centro de masa G y el centro de empuje E es perpendicular a superficie del agua MN. El producto escalar

${\displaystyle \begin{array}{l}\overrightarrow{EG}·\overrightarrow{MN}=0\\ \left\{\left(0-\left(-\frac{1}{2}+\frac{a}{3}\right)\right)\widehat{i}+\left(\frac{1}{2}-\frac{b}{3}\right)\widehat{j}\right\}·\left\{\left(a-\frac{1}{2}-\frac{-1}{2}\right)\widehat{i}+\left(0-b\right)\widehat{j}\right\}=0\\ \left\{\left(\frac{1}{2}-\frac{a}{3}\right)\widehat{i}+\left(\frac{1}{2}-\frac{b}{3}\right)\widehat{j}\right\}·\left\{a\widehat{i}-b\widehat{j}\right\}=\left(\frac{1}{2}-\frac{a}{3}\right)a-\left(\frac{1}{2}-\frac{b}{3}\right)b=0\\ a-b=\frac{2}{3}\left(a^2-b^2\right)\{\begin{array}{l}a-b=0\\ a+b=\frac{3}{2}\end{array}\end{array}}$

Los posibles ángulos θ de equilibrio son

${\displaystyle \{\begin{array}{l}\sqrt{\frac{2q}{\tan \theta }}=\sqrt{2q\tan \theta },\tan \theta =1\\ \sqrt{\frac{2q}{\tan \theta }}+\sqrt{2q\tan \theta }=\frac{3}{2},{\tan }^2\theta -\left(\frac{9}{8q}-2\right)\tan \theta +1=0\end{array}}$

Simplificamos la segunda expresión

${\displaystyle \begin{array}{l}\frac{1}{{\cos }^2\theta }-\left(\frac{9}{8q}-2\right)\frac{\sin \theta }{\cos \theta }=0\\ 1=\frac{1}{2}\left(\frac{9}{8q}-2\right)\sin (2\theta )\\ \sin (2\theta )=\frac{16q}{9-16q}\end{array}}$

El miembro derecho tiene que ser menor que la unidad 16q/(9-16q)<1, lo que implica que q<9/32

Para q=0.25, se despeja tanθ de la ecuación de segundo grado, obtenemos tanθ=1/2, que coincide con la sección anterior

Establidad

El criterio de estabilidad es que la distancia EG entre el centro de masa G y el centro de empuje E deberá ser mínima.

Antes hemos calculado el vector $\overrightarrow{EG}$ , el cuadrado de su módulo es

${\displaystyle d^2={\left(\frac{1}{2}-\frac{a}{3}\right)}^2+{\left(\frac{1}{2}-\frac{b}{3}\right)}^2=\frac{1}{8}+\frac{a^2+b^2}{9}-\frac{a+b}{3}}$

Denominamos t=tanθ. La derivada de d² respecto del ángulo t es

${\displaystyle \begin{array}{l}{d}^2=\frac{1}{8}+\frac{2q}{9}\left(\frac{1}{t}+t\right)-\frac{\sqrt{2q}}{3}\left(\frac{1}{\sqrt{t}}+\sqrt{t}\right)\\ \frac{d}{dt}{d}^2=\frac{2q}{9}\left(-\frac{1}{t^2}+1\right)-\frac{\sqrt{2q}}{3}\left(-\frac{1}{2}{t}^{-3/2}+\frac{1}{2}{t}^{-1/2}\right)=0\\ \frac{\sqrt{2q}}{3}\frac{(t+1)(t-1)}{t^2}-\frac{1}{2\sqrt{t}}\frac{t-1}{t}=0\{\begin{array}{l}t=1\\ t^2-\left(\frac{9}{8q}-2\right)t+1=0\end{array}\end{array}}$

El mismo resultado que en el apartado anterior. Calculamos la derivada segunda

${\displaystyle \frac{d^2}{d{t}^2}{d}^2=\frac{4q}{9}\frac{1}{t^3}-\frac{\sqrt{2q}}{12}\left(3t^{-5/2}-t^{-3/2}\right)}$

Signos de la derivada segunda

Representamos la derivada segunda en función de q para valores de t=tanθ

• t=1, en color azul, en el intervalo (0.25,0.5)

• $\sin (2\theta )=\frac{16q}{9-16q}$ , en color azul, en el intervalo (0.25,9/32) donde el miembro derecho es menor que la unidad

q=linspace(1/4,0.5,100);
t=1;
y=4*q./(9*t.^3)-sqrt(2*q).*(3*t.^(-5/2)-t.^(-3/2))/12;
hold on
plot(q,y)
q=linspace(0.25, 9/32,100);
th=asin(16*q./(9-16*q));
t=tan(th/2);
y=4*q./(9*t.^3)-sqrt(2*q).*(3*t.^(-5/2)-t.^(-3/2))/12;
plot(q,y)
line([9/32,9/32],[-0.01,0.06],'lineStyle','--','color','k')
hold off
xlabel('q')
legend('t=1','t','location','best')
ylabel('f''(q)')
grid on
title('Estabilidad')

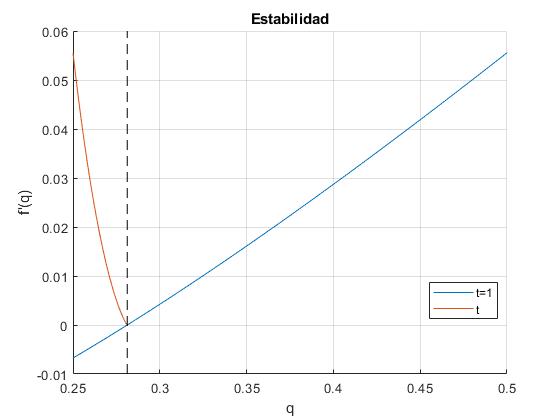
La derivada segunda es positiva, (mínimo) equilibrio estable para $\sin (2\theta )=\frac{16q}{9-16q}$ , en el intervalo (0.25,9/32)

Para tanθ=1, la derivada segunda es positiva si

${\displaystyle \begin{array}{l}\frac{4q}{9}-\frac{\sqrt{2q}}{12}2>0\\ q>\frac{9}{32}\end{array}}$

Equilibrio y estabilidad

Representamos gráficamente el ángulo θ en grados en función de q en el intervalo (0, 1/2). Teniendo en cuenta la dualidad q→(1-q) extendemos la representación gráfica al intervalo (1/2, 1)

hold on
line([0,(3-sqrt(3))/6],[0,0],'color','r')
q=linspace((3-sqrt(3))/6,1/4,50);
th=atand(2*sqrt(3*q-3*q.^2-1/2));
plot(q,th,'r')
q=linspace(1/4,9/32,50);
th=asind(16*q./(9-16*q))/2;
plot(q,th,'r')
line([9/32,1/2],[45,45],'color','r')
line([1-9/32,1/2],[45,45],'color','r')
q=linspace(1/4,9/32,50);
th=asind(16*q./(9-16*q))/2;
plot(1-q,th,'r')
q=linspace((3-sqrt(3))/6,1/4,50);
th=atand(2*sqrt(3*q-3*q.^2-1/2));
plot(1-q,th,'r')
line([1,1-(3-sqrt(3))/6],[0,0],'color','r')

line([(3-sqrt(3))/6,(3-sqrt(3))/6],[0,45],'lineStyle','--','color','k')
line([1/4,1/4],[0,45],'lineStyle','--','color','k')
line([9/32,9/32],[0,45],'lineStyle','--','color','k')
line([1-(3-sqrt(3))/6,1-(3-sqrt(3))/6],[0,45],'lineStyle','--','color','k')
line([3/4,3/4],[0,45],'lineStyle','--','color','k')
line([1-9/32,1-9/32],[0,45],'lineStyle','--','color','k')

hold off
grid on
xlabel('q')
ylabel('\theta')
title('Equilibrio')

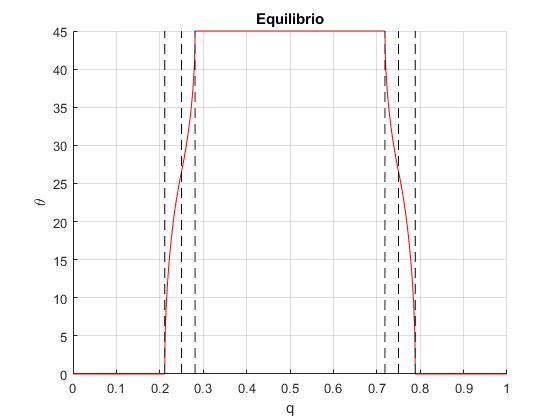
Ejemplos

Representamos la sección de la barra que flota para un valor de la densidad relativa q en cada uno de los intervalos de la tabla q≤1/2

En los ejemplos 2, 3 y 4, se calcula el punto Q de intersección de la recta que une el centro de empuje E y el centro de masa G con la superficie horizontal, recta MN. Se gira la figura un ángulo θ alrededor de un eje perpendicular a la sección cuadrada y que pasa por Q.

• Región 1, q=0.2

q=0.2;
hold on
line([-0.6,0.6],[0,0],'color','b')
line([-0.5,0.5],[-q,-q],'lineWidth',1.5,'color','r')
line([-0.5,0.5],[1-q,1-q],'lineWidth',1.5,'color','r')
line([-0.5,-0.5],[-q,1-q],'lineWidth',1.5,'color','r')
line([0.5,0.5],[-q,1-q],'lineWidth',1.5,'color','r')
plot(0,1/2-q,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
plot(0,-q/2,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b')
hold off
xlim([-1.25,1.25])
axis off
axis equal



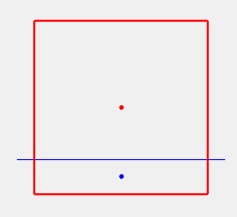
• Región 2, q=0.23

function flota_5
    q=0.23;
    delta=sqrt(3*q-3*q^2-1/2);
    th=atan(2*delta); %ángulo girado
    m1=-2*delta;
    b1=q;
    m2=-(3*q^2+delta^2-3*q)/delta;
    b2=-1/2;
    x0=(b1-b2)/(m2-m1);
    y0=(m2*b1-m1*b2)/(m2-m1);

    hold on
    line([-1,0.6],[0,0],'color','b')
    [x1,y1]=gira(-0.5,0);
    [x2,y2]=gira(0.5,0);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')
    [x1,y1]=gira(0.5,1);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')
    [x2,y2]=gira(-0.5,1);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')   
    [x1,y1]=gira(-0.5,0);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')

%centro de masa
    [x1,y1]=gira(0,1/2);
    plot(x1,y1,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
%centro empuje
    [x1,y1]=gira(-delta/(6*q),(3*q^2+delta^2)/(6*q));
    plot(x1,y1,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b')
    hold off
    xlim([-1.25,1.25])
    axis off
    axis equal
    
    function [X,Y]=gira(x,y)
        X=(x-x0)*cos(th)-(y-y0)*sin(th);
        Y=(x-x0)*sin(th)+(y-y0)*cos(th);
    end
end



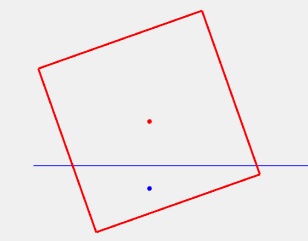
• Región 3, q=0.27

function flota_6
    q=0.27;
    th=asin(16*q/(9-16*q))/2; %ángulo girado
    a=sqrt(2*q/tan(th));
    b=sqrt(2*q*tan(th));

    m1=-b/a;
    b1=b*(a-1/2)/a;
    m2=(2*b-3)/(2*a-3);
    b2=1/2;
    x0=(b1-b2)/(m2-m1);
    y0=(m2*b1-m1*b2)/(m2-m1);
    hold on
    line([-0.6,0.8],[0,0],'color','b')
    [x1,y1]=gira(-0.5,0);
    [x2,y2]=gira(0.5,0);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')
    [x1,y1]=gira(0.5,1);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')
    [x2,y2]=gira(-0.5,1);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')
    [x1,y1]=gira(-0.5,0);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')

%centro de masa
    [x1,y1]=gira(0,1/2);
    plot(x1,y1,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
%centro empuje
    [x1,y1]=gira(a/3-1/2,b/3);
    plot(x1,y1,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b')
    hold off
    xlim([-1.25,1.25])
    axis off
    axis equal
 
    function [X,Y]=gira(x,y)
        X=(x-x0)*cos(th)-(y-y0)*sin(th);
        Y=(x-x0)*sin(th)+(y-y0)*cos(th);
    end
end



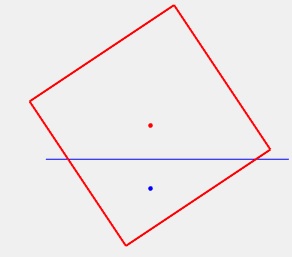
• Región 4, q=0.40

function flota_7
    q=0.4;
    th=pi/4; %ángulo girado
    a=sqrt(2*q/tan(th));
    b=sqrt(2*q*tan(th));

    m1=-b/a;
    b1=b*(a-1/2);
    m2=(2*b-3)/(2+a-3);
    b2=1/2;
    x0=(b1-b2)/(m2-m1);
    y0=(m2*b1-m1*b2)/(m2-m1);

    hold on
    line([-0.8,0.8],[0,0],'color','b')
    [x1,y1]=gira(-0.5,0);
    [x2,y2]=gira(0.5,0);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')
    [x1,y1]=gira(0.5,1);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')
    [x2,y2]=gira(-0.5,1);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')
    [x1,y1]=gira(-0.5,0);
    line([x1,x2],[y1,y2],'lineWidth',1.5,'color','r')

%centro de masa
    [x1,y1]=gira(0,1/2);
    plot(x1,y1,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
%centro empuje
    [x1,y1]=gira(a/3-1/2,b/3);
    plot(x1,y1,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b')
    hold off
    xlim([-1.25,1.25])
    axis off
    axis equal
    
    function [X,Y]=gira(x,y)
        X=(x-x0)*cos(th)-(y-y0)*sin(th);
        Y=(x-x0)*sin(th)+(y-y0)*cos(th);
    end    
end



El código del ejemplo 3 y 4 son similares, en el primero hay que calcular el ángulo θ, en el segundo el ángulo θ=π/4 (45°).

Actividades

Se introduce

• La densidad relativa q en el intervalo (0, 1), en el control titulado Densidad relativa

Se pulsa el botón titulado Nuevo y se observa uno de los ocho posibles estados de equilibrio

Referencias

Yonatan Feigel, Nikita Fuzailov. Floating of a long square bar: experiment vs theory. Eur. J. Phys. 42 (2021) 035011