Vaciado de un depósito abierto en forma de tronco de cono

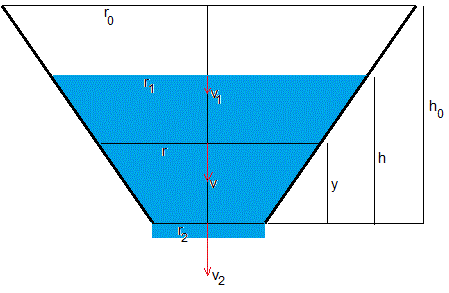
Sea un depósito en forma de tronco de cono invertido, de altura h₀ y de radios r₀ y r₂. Éste es el radio del orificio de salida del líquido contendido en el recipiente

Cuando la altura del líquido es h, la velocidad de la superficie libre es v₁ y la velocidad del fluido en el orificio de salida es v₂

Estado estacionario

Aplicamos la ecuación de Bernoulli en el estado estacionario a la línea de corriente que une los puntos (1) y (2) situados en la superficie libre del fluido y en el centro del orificio de salida.

$p_{1} + ρ g y_{1} + \frac{1}{2} ρ v_{1}^{2} = p_{2} + ρ g y_{2} + \frac{1}{2} ρ v_{2}^{2}$

Ahora bien, la presión en los puntos 1 y 2 es la atmosférica, p₁=p₂=p_atm, y₂=0, y₁=h. La ecuación de Bernoulli es

$2 g h + v_{1}^{2} = v_{2}^{2}$

La ecuación de continuidad

$ρ π r_{1}^{2} v_{1} = ρ π r_{2}^{2} v_{2}$

Eliminamos v₂ entre estas dos ecuaciones

$2 g h + v_{1}^{2} = {(\frac{r_{1}^{2} v_{1}}{r_{2}^{2}})}^{2}$

La geometría del tronco de cono nos permite establecer una relación entre los radios

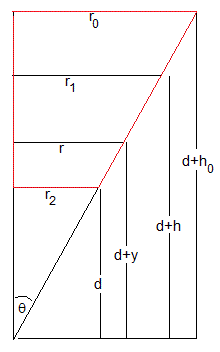
$\begin{array}{l} \tan θ = \frac{r_{2}}{d} = \frac{r}{d + y} = \frac{r_{1}}{d + h} = \frac{r_{0}}{d + h_{0}} \\ d = \frac{r_{2}}{r_{0} - r_{2}} h_{0} \\ r_{1} = r_{2} (1 + \frac{h}{d}) = r_{2} + \frac{r_{0} - r_{2}}{h_{0}} h = r_{2} + k h \\ r = r_{2} (1 + \frac{y}{d}) = r_{2} + k y \end{array}$

Por otra parte,

$v_{1} = \frac{d h}{d t}$

De este modo, llegamos a una ecuación diferencial es h

$\begin{array}{l} 2 g h + {(\frac{d h}{d t})}^{2} = {(\frac{r_{2} + k h}{r_{2}})}^{4} {(\frac{d h}{d t})}^{2} \\ {{(\frac{r_{2} + k h}{r_{2}})}^{4} - 1} {(\frac{d h}{d t})}^{2} - 2 g h = 0 \end{array}$

Con la condición inicial, en el instante t=0, la altura del fluido es h₀

Es conveniete expresar la ecuación diferencial en términos de las magnitudes adimensionales H y T

$H = \frac{k h}{r_{2}}, T = \sqrt{\frac{g k}{r_{2}}} t$

El resultado es

$\begin{array}{l} {{(\frac{r_{2} + k \frac{r_{2} H}{k}}{r_{2}})}^{4} - 1} \frac{{(\frac{r_{2}}{k})}^{2}}{\frac{r_{2}}{g k}} {(\frac{d H}{d T})}^{2} - 2 g \frac{r_{2} H}{k} = 0 \\ ({(1 + H)}^{4} - 1) \frac{g r_{2}}{k} {(\frac{d H}{d T})}^{2} - 2 g \frac{r_{2} H}{k} = 0 \\ (\frac{H^{3}}{2} + 2 H^{2} + 3 H + 2) {(\frac{d H}{d T})}^{2} - 1 = 0 \end{array}$

En el instante T=0

$H_{0} = \frac{k h_{0}}{r_{2}} = \frac{r_{0} - r_{2}}{h_{0}} \frac{h_{0}}{r_{2}} = \frac{r_{0}}{r_{2}} - 1$

Aproximación de Torricelli

Cuando la velocidad de la superficie libre del fluido v₁≈0. La ecuación de Bernoulli se expresa

$\begin{array}{l} 2 g h \approx v_{2}^{2} \\ v_{2} = - \sqrt{2 g h} \\ \frac{r_{1}^{2}}{r_{2}^{2}} v_{1} + \sqrt{2 g h} = 0 \\ \frac{r_{1}^{2}}{r_{2}^{2}} \frac{d h}{d t} + \sqrt{2 g h} = 0 \\ {(\frac{r_{2} + k h}{r_{2}})}^{2} \frac{d h}{d t} + \sqrt{2 g h} = 0 \end{array}$

Expresamos la ecuación diferencial en términos de las magnitudes adimensionales H y T

$\begin{array}{l} {(\frac{r_{2} + k \frac{r_{2} H}{k}}{r_{2}})}^{2} \frac{\frac{r_{2}}{k}}{\sqrt{\frac{r_{2}}{g k}}} \frac{d H}{d T} + \sqrt{2 g \frac{r_{2} H}{k}} = 0 \\ {(1 + H)}^{2} \frac{d H}{d T} + \sqrt{2 H} = 0 \end{array}$

Integrando

$\begin{array}{l} \frac{1}{\sqrt{2}} \int_{H_{0}}^{H} (\frac{1}{\sqrt{H}} + 2 \sqrt{H} + H^{3 / 2}) d H = - \int_{0}^{T} d T \\ T = - \frac{1}{\sqrt{2}} {(2 \sqrt{H} + \frac{4}{3} H^{3 / 2} + \frac{2}{5} H^{5 / 2}) |}_{H_{0}}^{H} \\ T = \sqrt{2 H_{0}} (1 + \frac{2}{3} H_{0} + \frac{1}{5} H_{0}^{2}) - \sqrt{2 H} (1 + \frac{2}{3} H + \frac{1}{5} H^{2}) \end{array}$

El depósito se vacía H=0 en el instante T_f

$T_{f} = \sqrt{2 H_{0}} (1 + \frac{2}{3} H_{0} + \frac{1}{5} H_{0}^{2})$

Estado no estacionario

Aplicamos la ecuación de Bernoulli en el estado no estacionario a la línea de corriente que une los puntos (1) y (2) situados en la superficie libre del fluido y en el centro del orificio de salida.

$(p_{1} + ρ g y_{1} + \frac{1}{2} ρ v_{1}^{2}) - (p_{2} + ρ g y_{2} + \frac{1}{2} ρ v_{2}^{2}) = \frac{d Q}{d t} \int_{1}^{2} \frac{d s}{A (s)}$

La ecuación de continuidad es

$Q = \frac{d m}{d t} = ρ π r^{2} v = ρ π r_{1}^{2} v_{1} = ρ π r_{2}^{2} v_{2}$

Ahora bien, la presión en los puntos 1 y 2 es la atmosférica, p₁=p₂=p_atm, y₂=0, y₁=h. La ecuación de Bernoulli es

$g h + \frac{1}{2} v_{1}^{2} - \frac{1}{2} v_{2}^{2} = \frac{d (r_{1}^{2} v_{1})}{d t} \int_{1}^{2} \frac{d y}{r^{2}}$

Eliminando v₂

$g h + \frac{1}{2} v_{1}^{2} - \frac{1}{2} {(\frac{r_{1}^{2} v_{1}}{r_{2}^{2}})}^{2} = \frac{d (r_{1}^{2} v_{1})}{d t} \int_{h}^{0} \frac{d y}{r^{2}}$

Teniendo en cuenta la relación entre los radios y que

$\begin{array}{l} v_{1} = \frac{d h}{d t} \\ \frac{d r_{1}}{d t} = k \frac{d h}{d t} \end{array}$

Obtenemos una ecuación diferencial en h

$\begin{array}{l} g h + \frac{1}{2} v_{1}^{2} - \frac{1}{2} {(\frac{r_{1}^{2} v_{1}}{r_{2}^{2}})}^{2} = (2 r_{1} v_{1} \frac{d r_{1}}{d t} + r_{1}^{2} \frac{d v_{1}}{d t}) \int_{h}^{0} \frac{d y}{{(r_{2} + k y)}^{2}} \\ g h + \frac{1}{2} {(\frac{d h}{d t})}^{2} - \frac{1}{2} {(\frac{r_{2} + k h}{r_{2}})}^{4} {(\frac{d h}{d t})}^{2} = (2 (r_{2} + k h) \frac{d h}{d t} k \frac{d h}{d t} + {(r_{2} + k h)}^{2} \frac{d^{2} h}{d t^{2}}) \frac{1}{k} (\frac{1}{r_{2} + k h} - \frac{1}{r_{2}}) \\ g h + \frac{1}{2} {(\frac{d h}{d t})}^{2} - \frac{1}{2} {(\frac{r_{2} + k h}{r_{2}})}^{4} {(\frac{d h}{d t})}^{2} = - (2 k {(\frac{d h}{d t})}^{2} + (r_{2} + k h) \frac{d^{2} h}{d t^{2}}) \frac{h}{r_{2}} \end{array}$

La integral del tipo $\int \frac{d u}{u^{2}} = - \frac{1}{u}$ , es inmediata

Las condiciones iniciales son, en el instante t=0, h=h₀ (recipiente lleno), dh/dt=0

Es conveniente expresar la ecuación diferencial en términos de las magnitudes adimensionales H y T

$\begin{array}{l} \frac{\frac{r_{2} H}{k}}{r_{2}} (r_{2} + k \frac{r_{2} H}{k}) \frac{\frac{r_{2}}{k}}{\frac{r_{2}}{g k}} \frac{d^{2} H}{d T^{2}} + (\frac{1}{2} - \frac{1}{2} {(\frac{r_{2} + k \frac{r_{2} H}{k}}{r_{2}})}^{4} + 2 k \frac{\frac{r_{2} H}{k}}{r_{2}}) \frac{{(\frac{r_{2}}{k})}^{2}}{\frac{r_{2}}{g k}} {(\frac{d H}{d t})}^{2} + g \frac{r_{2} H}{k} = 0 \\ \frac{H}{k} r_{2} (1 + H) g \frac{d^{2} H}{d T^{2}} + (\frac{1}{2} - \frac{1}{2} {(1 + H)}^{4} + 2 H) g \frac{r_{2}}{k} {(\frac{d H}{d T})}^{2} + g \frac{r_{2} H}{k} = 0 \\ H (1 + H) \frac{d^{2} H}{d T^{2}} + (\frac{1}{2} - \frac{1}{2} {(1 + H)}^{4} + 2 H) {(\frac{d H}{d T})}^{2} + H = 0 \\ (1 + H) \frac{d^{2} H}{d T^{2}} - (\frac{H^{3}}{2} + 2 H^{2} + 3 H) {(\frac{d H}{d T})}^{2} + 1 = 0 \end{array}$

Se resuelve esta ecuación diferencial con las condiciones iniciales, en el instante T=0, H=H₀, dH/dT=0

Las velocidades adimensionales V₁ en la superficie libre y del fluido V₂ en el orificio de salida son

$\begin{array}{l} v_{1} = \frac{d h}{d t} = \frac{\frac{r_{2}}{k}}{\sqrt{\frac{r_{2}}{g k}}} \frac{d H}{d T} = \sqrt{\frac{g r_{2}}{k}} \frac{d H}{d T} \\ v_{2} = {(\frac{r_{1}}{r_{2}})}^{2} v_{1} = {(\frac{r_{2} + k h}{r_{2}})}^{2} v_{1} = {(\frac{r_{2} + k \frac{r_{2} H}{k}}{r_{2}})}^{2} v_{1} = {(1 + H)}^{2} \sqrt{\frac{g r_{2}}{k}} \frac{d H}{d T} \\ {\begin{cases} V_{1} = \frac{d H}{d T} \\ V_{2} = {(1 + H)}^{2} \frac{d H}{d T} \end{cases} \end{array}$

Resultados

Representamos la altura H del fluido en función del tiempo T, sabiendo que en el instante T=0, H=H₀ y dH/dT=0. Para ello, resolvemos las ecuaciones diferenciales

Estado estacionario (solución aproximada)

$(\frac{H^{3}}{2} + 2 H^{2} + 3 H + 2) {(\frac{d H}{d T})}^{2} - 1 = 0$

Estado no estacionario (solución exacta)

$(1 + H) \frac{d^{2} H}{d T^{2}} - (\frac{H^{3}}{2} + 2 H^{2} + 3 H) {(\frac{d H}{d T})}^{2} + 1 = 0$

Ejemplo, H₀=4

function funnel
    H0=4;    
    f=@(t,x) -1/sqrt(x^3/2+2*x^2+3*x+2); 
    opts=odeset('events',@stop_fluido);
    [t,x]=ode45(f,[0,100],H0, opts); 
    Tf=sqrt(2*H0)*(1+2*H0/3+H0^2/5); %tiempo de vaciado aproximado
    disp(Tf)
    hold on
    plot(t,x)
    g=@(t,x) [x(2); -1/(1+x(1))+(x(1)^3/2+2*x(1)^2+3*x(1))*x(2)^2/(1+x(1))];
    [t,x]=ode45(g,[0,100],[H0,0], opts); 
    plot(t,x(:,1))
    hold off
    grid on
    legend('aproximado','exacto','Location','best')
    xlabel('T')
    ylabel('H');
    title('Descarga')

    function [value,isterminal,direction]=stop_fluido(~,x)
        value=x(1);
        isterminal=1; %1 detiene la integración cuando la altura H se hace cero   
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
end

Tiempo que tarda en vaciarse el depósito (aproximado)

   19.4219

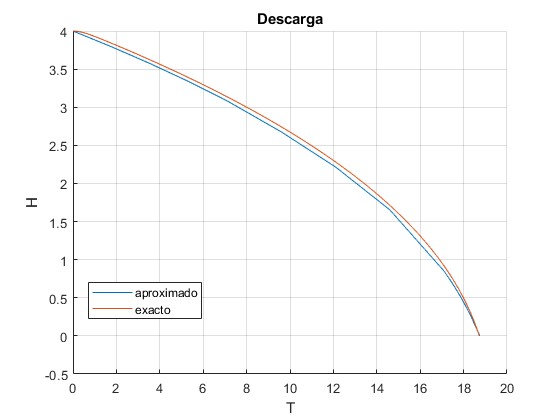
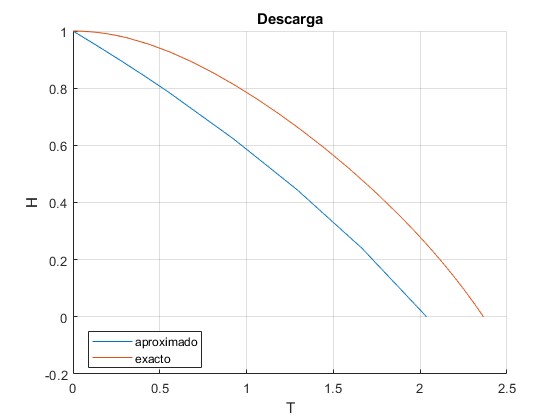
Cambiamos H₀=1, aprecimos que la solución exacta difiere de la aproximada

   2.6399

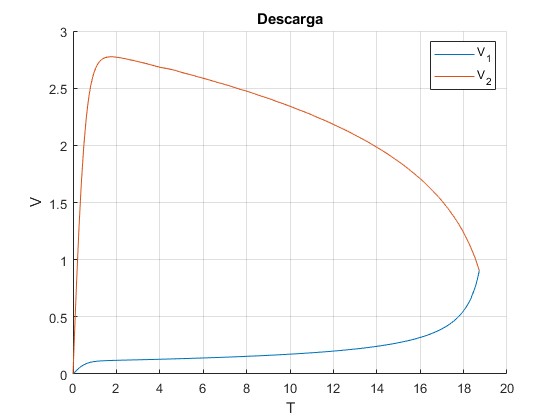
Representamos las velocidades adimensionales V₁ y V₂ del fluido en función del tiempo T.

Para H₀=4

function funnel_1
    H0=4;    
    g=@(t,x) [x(2); -1/(1+x(1))+(x(1)^3/2+2*x(1)^2+3*x(1))*x(2)^2/(1+x(1))];
    opts=odeset('events',@stop_fluido);
    [t,x]=ode45(g,[0,100],[H0,0], opts); 
    hold on
    plot(t,x(:,2))
    plot(t,x(:,2).*(1+x(:,1)).^2)
    hold off
    grid on
    xlabel('T')
    legend('V_1','V_2','Location','best')
    ylabel('V');
    title('Descarga')

    function [value,isterminal,direction]=stop_fluido(~,x)
        value=x(1);
        isterminal=1;    
        direction=-1; 
    end
end

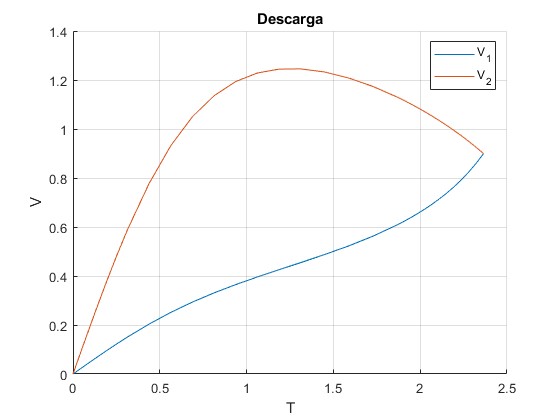
Para H₀=1

Otras geometrías

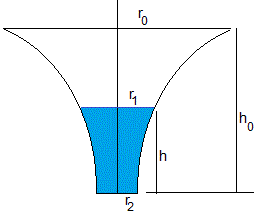
El área de la sección del recipiente viene descrita por la función A(y)

El área del orificio de salida es A₂=A(0). La sección del recipiente a una altura h es A₁=A(h)

$(p_{1} + ρ g y_{1} + \frac{1}{2} ρ v_{1}^{2}) - (p_{2} + ρ g y_{2} + \frac{1}{2} ρ v_{2}^{2}) = \frac{d Q}{d t} \int_{1}^{2} \frac{d s}{A (s)}$

La ecuación de continuidad es

$Q = \frac{d m}{d t} = ρ A_{1} v_{1} = ρ A_{2} v_{2}$

Ahora bien, la presión en los puntos 1 y 2 es la atmosférica, p₁=p₂=p_atm, y₂=0, y₁=h. La ecuación de Bernoulli es

$\begin{array}{l} g h + \frac{1}{2} v_{1}^{2} = \frac{1}{2} v_{2}^{2} + \frac{d (A_{1} v_{1})}{d t} \int_{h}^{0} \frac{d y}{A (y)} \\ A_{1} = A (h), A_{2} = A (0), v_{1} = \frac{d h}{d t} \end{array}$

El resultado es

$\begin{array}{l} \frac{d (A (h) v_{1})}{d t} = \frac{d A (h)}{d t} (\frac{d h}{d t}) + A (h) (\frac{d^{2} h}{d t^{2}}) = \frac{d A (h)}{d h} \frac{d h}{d t} (\frac{d h}{d t}) + A (h) (\frac{d^{2} h}{d t^{2}}) = \frac{d A (h)}{d h} {(\frac{d h}{d t})}^{2} + A (h) \frac{d^{2} h}{d t^{2}} \\ g h + \frac{1}{2} {(\frac{d h}{d t})}^{2} = \frac{1}{2} {(\frac{A (h)}{A (0)})}^{2} {(\frac{d h}{d t})}^{2} - (\frac{d A (h)}{d h} {(\frac{d h}{d t})}^{2} + A (h) \frac{d^{2} h}{d t^{2}}) \int_{0}^{h} \frac{d y}{A (y)} \\ g h + \frac{1}{2} (1 - {(\frac{A (h)}{A (0)})}^{2}) {(\frac{d h}{d t})}^{2} + (\frac{d A (h)}{d h} {(\frac{d h}{d t})}^{2} + A (h) \frac{d^{2} h}{d t^{2}}) \int_{0}^{h} \frac{d y}{A (y)} = 0 \end{array}$

Se resuelve la ecuación diferencial, con las condiciones iniciales t=0, h=h₀, dh/dt=0

Ejemplo 1.

La sección del recipiente viene descrita por la función cuadrática

$A (y) = A_{2} {(1 + k \frac{y}{h_{0}})}^{2}$

Que corresponde a un tronco de cono, descrito en la sección anterior. A(0)=A₂. Resolvemos la inetegral

$\int_{0}^{h} \frac{d y}{A (y)} = \frac{1}{A_{2}} \int_{0}^{h} \frac{d y}{{(1 + k \frac{y}{h_{0}})}^{2}} = - \frac{1}{A_{2}} (- \frac{h_{0}}{k}) (\frac{1}{1 + k \frac{h}{h_{0}}} - 1) = \frac{1}{A_{2}} \frac{h}{1 + k \frac{h}{h_{0}}}$

La ecuación diferencial es

$\begin{array}{l} g h + \frac{1}{2} (1 - {(\frac{A_{2} {(1 + k \frac{h}{h_{0}})}^{2}}{A_{2}})}^{2}) {(\frac{d h}{d t})}^{2} + (A_{2} 2 \frac{k}{h_{0}} (1 + k \frac{h}{h_{0}}) {(\frac{d h}{d t})}^{2} + A_{2} {(1 + k \frac{h}{h_{0}})}^{2} \frac{d^{2} h}{d t^{2}}) (\frac{1}{A_{2}} \frac{h}{1 + k \frac{h}{h_{0}}}) = 0 \\ g h + \frac{1}{2} (1 - {(1 + k \frac{h}{h_{0}})}^{4}) {(\frac{d h}{d t})}^{2} + (2 \frac{k}{h_{0}} {(\frac{d h}{d t})}^{2} + (1 + k \frac{h}{h_{0}}) \frac{d^{2} h}{d t^{2}}) h = 0 \\ g h - \frac{1}{2} (6 k^{2} \frac{h^{2}}{h_{0}^{2}} + k^{4} \frac{h^{4}}{h_{0}^{4}} + 4 k \frac{h}{h_{0}} + 4 k^{3} \frac{h^{3}}{h_{0}^{3}} - 4 k \frac{h}{h_{0}}) {(\frac{d h}{d t})}^{2} + (1 + k \frac{h}{h_{0}}) h \frac{d^{2} h}{d t^{2}} = 0 \\ \frac{d^{2} h}{d t^{2}} - \frac{\frac{k^{2}}{h_{0}^{2}} h (3 + \frac{1}{2} k^{2} \frac{h^{2}}{h_{0}^{2}} + 2 k \frac{h}{h_{0}})}{1 + k \frac{h}{h_{0}}} {(\frac{d h}{d t})}^{2} + \frac{g}{1 + k \frac{h}{h_{0}}} = 0 \end{array}$

Es conveniente expresar la ecuación diferencial en términos de las magnitudes adimensionales H y T

$\begin{array}{l} H = \frac{h}{h_{0}}, T = \sqrt{\frac{g}{h_{0}}} t \\ \frac{d^{2} H}{d T^{2}} - \frac{k^{2} H (3 + \frac{1}{2} k^{2} H^{2} + 2 k H)}{1 + k H} {(\frac{d H}{d T})}^{2} + \frac{1}{1 + k H} = 0 \end{array}$

Ejemplo 2.

La sección del recipiente viene descrita por la función exponencial

$A (y) = A_{2} \exp (α \frac{y}{h_{0}})$

Resolvemos la integral

$\int_{0}^{h} \frac{d y}{A (y)} = \frac{1}{A_{2}} \int_{0}^{h} \frac{d y}{\exp (α \frac{y}{h_{0}})} = - \frac{1}{A_{2}} \frac{h_{0}}{α} (\exp (- α \frac{h}{h_{0}}) - 1) = \frac{1}{A_{2}} \frac{h_{0}}{α} (1 - \exp (- α \frac{h}{h_{0}}))$

La ecuación diferencial es

$\begin{array}{l} g h + \frac{1}{2} (1 - {(\frac{A_{2} \exp (α \frac{h}{h_{0}})}{A_{2}})}^{2}) {(\frac{d h}{d t})}^{2} + (A_{2} \frac{α}{h_{0}} \exp (α \frac{h}{h_{0}}) {(\frac{d h}{d t})}^{2} + A_{2} \exp (α \frac{h}{h_{0}}) \frac{d^{2} h}{d t^{2}}) (\frac{1}{A_{2}} \frac{h_{0}}{α} (1 - \exp (- α \frac{h}{h_{0}}))) = 0 \\ g h + \frac{1}{2} (1 - \exp (2 α \frac{h}{h_{0}})) {(\frac{d h}{d t})}^{2} + (\exp (α \frac{h}{h_{0}}) {(\frac{d h}{d t})}^{2} + \frac{h_{0}}{α} \exp (α \frac{h}{h_{0}}) \frac{d^{2} h}{d t^{2}} - {(\frac{d h}{d t})}^{2} - \frac{h_{0}}{α} \frac{d^{2} h}{d t^{2}}) = 0 \\ g h + \frac{1}{2} (1 - \exp (2 α \frac{h}{h_{0}}) + 2 \exp (α \frac{h}{h_{0}}) - 2) {(\frac{d h}{d t})}^{2} + \frac{h_{0}}{α} (\exp (α \frac{h}{h_{0}}) - 1) \frac{d^{2} h}{d t^{2}} = 0 \\ g h - \frac{1}{2} (1 + \exp (2 α \frac{h}{h_{0}}) - 2 \exp (α \frac{h}{h_{0}})) {(\frac{d h}{d t})}^{2} + \frac{h_{0}}{α} (\exp (α \frac{h}{h_{0}}) - 1) \frac{d^{2} h}{d t^{2}} = 0 \\ g h - \frac{1}{2} {(\exp (α \frac{h}{h_{0}}) - 1)}^{2} {(\frac{d h}{d t})}^{2} + \frac{h_{0}}{α} (\exp (α \frac{h}{h_{0}}) - 1) \frac{d^{2} h}{d t^{2}} = 0 \\ \frac{d^{2} h}{d t^{2}} - \frac{1}{2} \frac{α}{h_{0}} (\exp (α \frac{h}{h_{0}}) - 1) {(\frac{d h}{d t})}^{2} + \frac{α}{h_{0}} \frac{g h}{(\exp (α \frac{h}{h_{0}}) - 1)} = 0 \end{array}$

Es conveniente expresar la ecuación diferencial en términos de las magnitudes adimensionales H y T

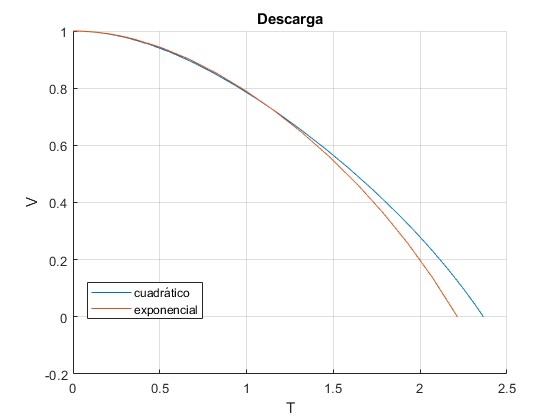
$\begin{array}{l} H = \frac{h}{h_{0}}, T = \sqrt{\frac{g}{h_{0}}} t \\ \frac{d^{2} H}{d T^{2}} - \frac{α}{2} (\exp (α H) - 1) {(\frac{d H}{d T})}^{2} + \frac{α H}{\exp (α H) - 1} = 0 \end{array}$

Resolvemos las dos ecuaciones diferenciales con las condiciones iniciales T=0, H=1, dH/dT=0

El la primera tomamos, k=1, en la segunda α=ln(4)

function funnel_2
    H0=1;    
    k=1;
    f=@(t,x) [x(2); k^2*x(1)*(3+k^2*x(1)^2/2+2*k*x(1))*x(2)^2/
(1+k*x(1))-1/(1+k*x(1))];
    opts=odeset('events',@stop_fluido);
    [t,x]=ode45(f,[0,100],[H0,0], opts); 
    hold on
    plot(t,x(:,1))
    alfa=log(4);
    g=@(t,x) [x(2); alfa*(exp(alfa*x(1))-1)*x(2)^2/2-alfa*x(1)/
(exp(alfa*x(1))-1)];
    [t,x]=ode45(g,[0,100],[H0,0], opts); 
    plot(t,x(:,1))
    hold off
    grid on
    xlabel('T')
    legend('cuadrático','exponencial','Location','best')
    ylabel('V');
    title('Descarga')

    function [value,isterminal,direction]=stop_fluido(~,x)
        value=x(1);
        isterminal=1;    
        direction=-1; 
    end
end

Referencias

Johann Otto, Carl E Mungan. Flow of water out of a funnel. Eur. J. Phys. 45 (2024) 055007

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017

H. Johari, W. W. Durgin. Unsteady flow in vertical, converging tubes