Se tapa con un dedo el extremo de un tubo de vidrio de radio R y altura H y se introduce en depósito grande de líquido de densidad ρ y viscosidad η, hasta una profundidad h.

Supondremos que el radio del tubo R es suficientemente grande para despreciar los efectos de la capilaridad

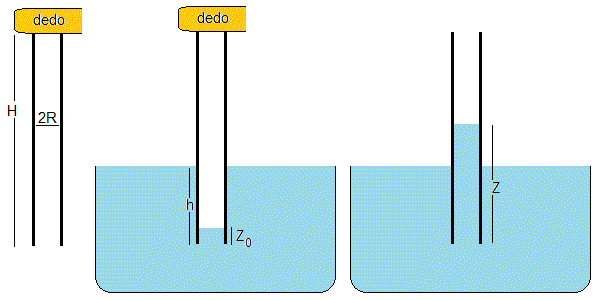
Situación inicial

En la situación inicial, tenemos un volumen πR²H de aire a la presión atmosférica p₀. Al introducirlo en el líquido, el volumen se reduce (H-Z₀)πR². Suponiendo una transformación isoterma

${\displaystyle \begin{array}{l}{p}_0\pi R^{2}H=\left(p_0+\rho g\left(h-Z_0\right)\right)\pi R^2\left(H-Z_0\right)\\ Z_0^2-\left(\frac{p_0}{\rho g}+H+h\right)Z_0+hH=0\\ Z_0=\frac{\frac{p_0}{\rho g}+H+h-\sqrt{\left(\frac{p_0}{\rho g}+H+h\right)-4hH}}{2}\end{array}}$

Si el líquido es agua, ρ=1000 kg/m³, la altura del tubo es H=20 cm y la profundidad a la que se sumerge es h=10 cm. Obtenemos Z₀=0.1881 cm

Si despreciamos Z₀ frente a h o H la ecuación es más simple

${\displaystyle \begin{array}{l}{p}_0\pi R^{2}H=\left(p_0+\rho gh\right)\pi R^2\left(H-Z_0\right)\\ Z_0=\frac{hH}{\frac{p_0}{\rho g}+h}\end{array}}$

El valor que obtenemos es Z₀=0.1916 cm

Análisis en términos de fuerzas

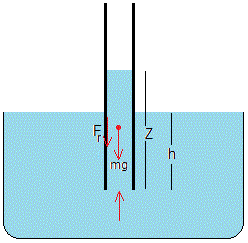
La masa de la columna de líquido es variable, m=ρπR²Z

Las fuerzas que actúan sobre la columna de líquido son

• El peso, mg, actúa en el centro de masas de la columna de líquido
• La fuerza que ejerce la presión hidrostática en la parte inferior del tubo, ρgh(πR²)
• Supondremos que actúa una fuerza de rozamiento proporcional a la velocidad, F_r=b'v

La segunda ley de Newton para un sistema de masa variable se escribe

${\displaystyle \begin{array}{l}\frac{d\left(mv\right)}{dt}=-mg+\rho gh\left(\pi R^2\right)-b^{\text{'}}v,v=\frac{dZ}{dt},m=\rho \left(\pi R^{2}Z\right)\\ \rho \left(\pi R^2\frac{dZ}{dt}\right)\frac{dZ}{dt}+\rho \left(\pi R^{2}Z\right)\frac{d^{2}Z}{d{t}^2}=-\rho \left(\pi R^{2}Z\right)g+\rho gh\left(\pi R^2\right)-b^{\text{'}}\frac{dZ}{dt}\\ Z\frac{d^{2}Z}{d{t}^2}+{\left(\frac{dZ}{dt}\right)}^2=gh-gZ-b\frac{dZ}{dt},b=\frac{b^{\text{'}}}{\pi R^2\rho }\end{array}}$

Más adelante resolveremos esta ecuación diferencial por procedimientos numéricos.

Experimento

Accedemos a la página web, https://github.com/r31415smith/AdvLab/tree/master/fluid_osc, que contiene la dirección del video de la experiencia https://www.youtube.com/watch?v=8FPFSC4cGGM.

Se ha medido la altura Z de la columna de fluido en mm en función del tiempo en s. Los datos se encuentran en el fichero 7924.dat. Copiamos los datos y los guardamos en un fichero de extensión .txt, denominado columna.txt

Importamos las tres columnas de datos, pulsando en el menú Home/Import data, elegimos el fichero que contiene las medidas.

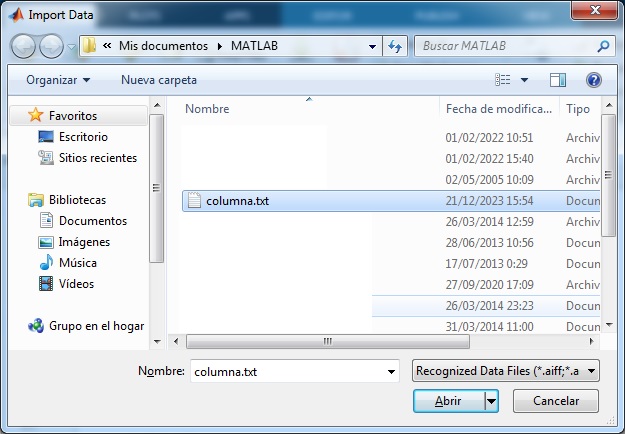
En el cuadro de diálogo que aparece, seleccionamos en Output Type, la opción Column vectors. Pulsamos el botón Import data

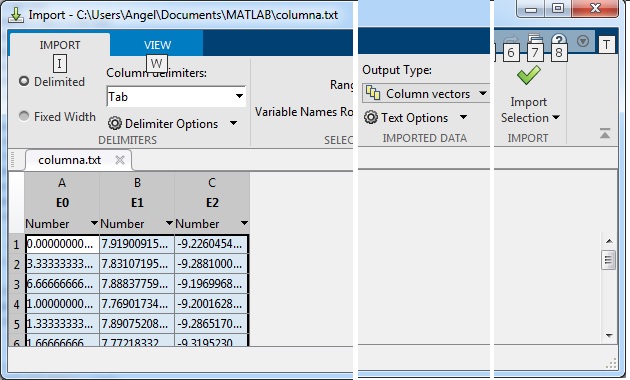
En la ventana Workspace aparecen tres vectores E0, E1 y E2.

Los datos relevantes son los tiempos, contenidos en el vector E0 y las correspondientes alturas de la columna de fluido, en el vector E2. La posición horizontal del tubo de vidrio carece de interés, por lo que eliminamos el vector E1 de la ventana Workspace

El instante inicial, t₀=0.267 es aquél en el que se retira el dedo que tapa el extremo superior del tubo y la columna de líquido empieza a ascender por el tubo

Los datos relevantes t>t₀, empiezan en la fila 9

Representamos las medidas Z altura de la columna de líquido en cm en función del tiempo t-t₀ en s

tt=E0(9:end)-0.267;
zz=E2(9:end)/10;
plot(tt,zz,'ko','markersize',3,'markerfacecolor','k')
grid on
ylabel('z (cm)')
xlabel('t (s)')
title('Oscilaciones de una columna de líquido')

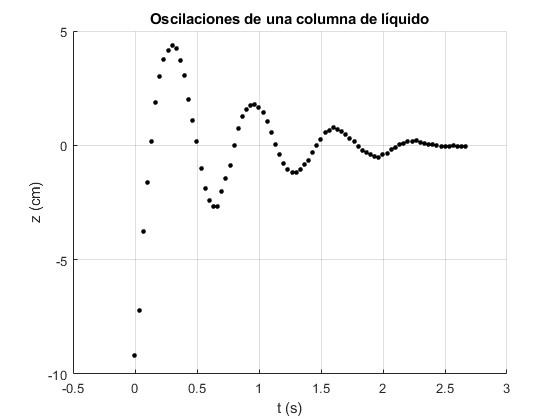
Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, Z=Z₀=0.2 cm, y dZ/dt=0, parte del reposo.

${\displaystyle \frac{d^{2}Z}{d{t}^2}=-\frac{1}{Z}\left({\left(\frac{dZ}{dt}\right)}^2-gh+gZ+b\frac{dZ}{dt}\right)}$

Con los siguientes datos

• parámetro b=23, que mejor ajusta a las medidas experimentales
• profundidad del extremo inferior del tubo, h=10 cm
• aceleración de la gravedad, g=980 cm/s²

tt=E0(9:end)-0.267;
zz=E2(9:end)/10;
h=10;
b=23;
hold on
plot(tt,zz,'ko','markersize',3,'markerfacecolor','k')
fN=@(t,x) [x(2);-(x(2)^2+980*x(1)-980*h+b*x(2))/x(1)]; 
[t,x]=ode45(fN,[0,3],[0.02,0]);
plot(t,x(:,1)-h,'r')
hold off
grid on
ylabel('z (cm)')
xlabel('t (s)')
title('Oscilaciones de una columna de líquido')

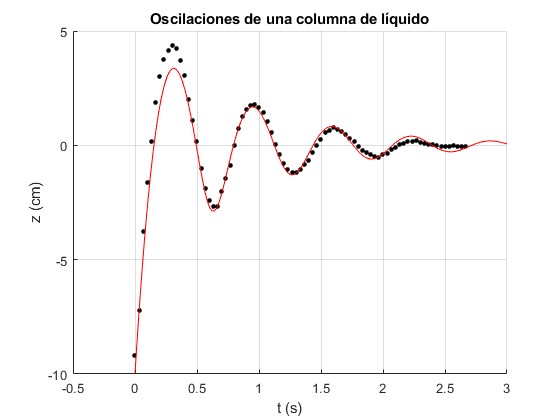
El modelo describe bastante bien las oscilaciones de la columna de líquido para el parámetro b=23

Análisis en términos de energías

Las fuerza que actúan sobre la columna de líquido son

• El peso, ρgZ(πR²), actúa en el centro de masas de la columna de líquido
• La fuerza que ejerce la presión hidrostática en la parte inferior del tubo, ρgh(πR²)

La diferencia es la fuerza neta sobre la columna de líquido

${\displaystyle F=\rho g\pi R^2\left(h-Z\right)}$

Es una fuerza que depende de la posición Z, similar a un muelle elástico. La energía potencial es

${\displaystyle \begin{array}{l}F=-\frac{d{E}_p}{dZ}\\ E_P(Z)-E_p(h)=-{\displaystyle \underset{h}{\overset{Z}{\int }}\rho g\pi R^2\left(h-Z\right)dZ}\\ E_P(Z)=\rho g\pi R^2\left(\frac{1}{2}{Z}^2-hZ\right)+\text{cte}\end{array}}$

La energía potencial está definida salvo una constante aditiva que tomaremos como cero

La energía total es la suma de cinética y potencial

${\displaystyle E=\frac{1}{2}\left(\rho \pi R^{2}Z\right){\left(\frac{dZ}{dt}\right)}^2+\rho g\pi R^2\left(\frac{1}{2}{Z}^2-hZ\right)}$

Expresamos la energía en términos de magnitudes adimensionales z y τ

${\displaystyle z=\frac{Z}{h},t=\tau \sqrt{\frac{H}{g}}}$

El resultado es

${\displaystyle \begin{array}{l}E=\frac{1}{2}\rho \pi R^2{h}^{3}z\frac{g}{h}{\left(\frac{dz}{d\tau }\right)}^2+\rho g\pi R^2\left(\frac{1}{2}{z}^2{h}^2-h^{2}z\right)\\ e=\frac{1}{2}z{\left(\frac{dz}{d\tau }\right)}^2+\frac{1}{2}{z}^2-z,e=\frac{E}{\rho \pi R^2{h}^{2}g}\end{array}}$

Conservación de la energía

Supongamos que no hay pérdidas, la energía se conserva

Para z=0, e=0. Integramos la ecuación diferencial

${\displaystyle \begin{array}{l}\frac{1}{2}z{\left(\frac{dz}{d\tau }\right)}^2+\frac{1}{2}{z}^2-z=0\\ \frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^2+\frac{1}{2}z-1=0\\ {\displaystyle \underset{0}{\overset{z}{\int }}\frac{dz}{\sqrt{2-z}}}={\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }\\ -2\sqrt{2-z}+2\sqrt{2}=\tau \end{array}}$

Elevando al cuadrado despejamos z

${\displaystyle \begin{array}{l}{\left(\sqrt{2}-\frac{\tau }{2}\right)}^2=2-z\\ z=\tau \left(\sqrt{2}-\frac{\tau }{4}\right),0\le \tau \le 4\sqrt{2}\end{array}}$

Las oscilaciones tienen un periodo de $4\sqrt{2}$. La altura máxima es z=2 que se produce en el instante $2\sqrt{2}$

Representamos las oscilaciones hasta el tiempo τ=30

f=@(t) t.*(sqrt(2)-t/4);
P=4*sqrt(2); %periodo
pf=@(t) f(t-P*floor(t/P)); %función periódica
fplot(pf,[0,20])
grid on
ylim([0,2.1])
xlabel('\tau')
ylabel('z')
title('Oscilaciones de una columna de líquido')

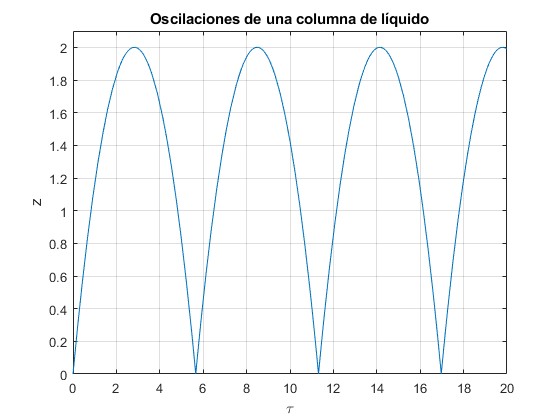
Disipación de la energía

Sin embargo, la experiencia nos muestra una oscilación cuya amplitud disminuye con el tiempo

1. Cuando el líquido entra y sale por la parte inferior del tubo

Cuando el líquido entra en el tubo o sale hay una pérdida de presión Δp debida al diferencia de radio entre el depósito (muy grande) y el tubo (radio pequeño). Debido a la abrupta contracción entre los dos, aparecen remolinos en la base del tubo, disipando cierta cantidad de energía. Cuando el cociente entre el radio del tubo y del depósito tiende a cero (como en esta experiencia)

${\displaystyle \Delta p=\frac{1}{2}\rho {\left(\frac{dZ}{dt}\right)}^2}$

es igual a la energía cinética por unidad de volumen. La energía asociada es negativa y tiene distinto signo dependiendo si dZ>0 (va hacia arriba) o dZ<0 hacia abajo

${\displaystyle \{\begin{array}{l}dE=-\Delta p·\left(\pi R^{2}dZ\right),dZ>0\\ dE=\Delta p·\left(\pi R^{2}dZ\right),dZ<0\end{array}}$

En términos de las unidades adimensionales z y τ

${\displaystyle \begin{array}{l}dE=\frac{1}{2}\pi R^2\rho h^3\frac{g}{h}{\left(\frac{dz}{d\tau }\right)}^{2}dz\\ de=\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^{2}dz,de=\frac{dE}{\rho \pi R^2{h}^{2}g}\\ \{\begin{array}{l}d{e}_1=-\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^{2}dz,dz>0\\ d{e}_1=\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^{2}dz,dz<0\end{array}\end{array}}$

2. Cuando la columna de líquido asciende o desciende por el tubo

Aplicamos la ley de Poiseuille, tal como lo hemos hecho para estudiar como asciende una columna de líquido en un tubo capilar impulsada por la fuerza que ejerce la tensión superficial

${\displaystyle \begin{array}{l}G=\frac{\pi }{8}\frac{\Delta p}{\eta }\frac{R^4}{Z}\\ \pi R^2\frac{dZ}{dt}=\frac{\pi }{8}\frac{\Delta p}{\eta }\frac{R^4}{Z}\\ \Delta p=\frac{8\eta }{R^2}Z\frac{dZ}{dt}\end{array}}$

La energía disipada es

${\displaystyle dE=-\Delta p·\left(\pi R^{2}dZ\right)=\frac{8\eta }{R^2}Z\frac{dZ}{dt}\left(\pi R^{2}dZ\right)}$

En términos de las unidades adimensionales z y τ

${\displaystyle \begin{array}{l}dE=-8\pi \eta h^{3}z\sqrt{\frac{g}{h}}\frac{dz}{d\tau }dz\\ d{e}_2=-\Omega z\frac{dz}{d\tau }dz,\Omega =\frac{8\eta }{\rho R^2}\sqrt{\frac{h}{g}}\end{array}}$

que es independiente de que el líquido ascienda o descienda, ya que (dz/dτ)dz es siempre positivo

• Densidad del agua, ρ=1000 kg/m³
• Viscosidad, η=1.002·10^-3 Pa·s
• Radio del tubo, R= 5 mm
• Profundidad, h= 10 cm

Con estos datos obtenemos Ω=0.0324

Nota: El valor del parámetro Ω que se proporciona en el artículo de Elise Lorenceau (ecuación 16) es

${\displaystyle \Omega =\frac{16\eta }{\rho R^2}\sqrt{\frac{h}{g}}}$

Dada la expresión de la energía e calculamos de

${\displaystyle \begin{array}{l}e=\frac{1}{2}z{\left(\frac{dz}{d\tau }\right)}^2+\frac{1}{2}{z}^2-z\\ de=\frac{de}{d\tau }d\tau =\left(\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^3+z\frac{dz}{d\tau }\frac{d^{2}z}{d{\tau }^2}+z\frac{dz}{d\tau }-\frac{dz}{d\tau }\right)d\tau \end{array}}$

• Para el movimiento hacia arriba, dz/dτ>0

${\displaystyle \begin{array}{l}\left(\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^3+z\frac{dz}{d\tau }\frac{d^{2}z}{d{\tau }^2}+z\frac{dz}{d\tau }-\frac{dz}{d\tau }\right)d\tau =-\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^{2}dz-\Omega z\frac{dz}{d\tau }dz,\frac{dz}{d\tau }>0\\ \frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^3+z\frac{dz}{d\tau }\frac{d^{2}z}{d{\tau }^2}+z\frac{dz}{d\tau }-\frac{dz}{d\tau }=-\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^3-\Omega z{\left(\frac{dz}{d\tau }\right)}^2\\ z\frac{d^{2}z}{d{\tau }^2}+{\left(\frac{dz}{d\tau }\right)}^2+z-1+\Omega z\frac{dz}{d\tau }=\mathrm{0,}\frac{dz}{d\tau }>0\end{array}}$

• Para el movimiento hacia abajo, dz/dτ<0

${\displaystyle \begin{array}{l}\left(\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^3+z\frac{dz}{d\tau }\frac{d^{2}z}{d{\tau }^2}+z\frac{dz}{d\tau }-\frac{dz}{d\tau }\right)d\tau =\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^{2}dz-\Omega z\frac{dz}{d\tau }dz,\frac{dz}{d\tau }<0\\ \frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^3+z\frac{dz}{d\tau }\frac{d^{2}z}{d{\tau }^2}+z\frac{dz}{d\tau }-\frac{dz}{d\tau }=\frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^3-\Omega z{\left(\frac{dz}{d\tau }\right)}^2\\ z\frac{d^{2}z}{d{\tau }^2}+z-1+\Omega z\frac{dz}{d\tau }=\mathrm{0,}\frac{dz}{d\tau }<0\end{array}}$

Resolvemos las ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\frac{d^{2}z}{d{\tau }^2}=\frac{1}{z}-1-\frac{1}{z}{\left(\frac{dz}{d\tau }\right)}^2,\frac{dz}{d\tau }>0\\ \frac{d^{2}z}{d{\tau }^2}=\frac{1}{z}-\mathrm{1,}\frac{dz}{d\tau }<0\end{array}}$

por procedimientos numéricos con las siguientes condiciones iniciales, τ=0, z=0.001, para tres valores del parámetro Ω=0, 0.3 y 3

hold on
for Omega=[0,0.3,2]
    [t,x]=ode45(@fL,[0,25],[0.001,0],[],Omega);
    plot(t,x(:,1), 'displayName',num2str(Omega))
end
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('\tau')
ylabel('z')
title('Oscilaciones de una columna de líquido')

Definimos la función fL a integrar

function dif_2=fL(~,x,p)
    Omega=p;
    if x(2)>0
            dif_2=[x(2); 1/x(1)-1-Omega*x(2)-x(2)^2/x(1)];
    else
            dif_2=[x(2); 1/x(1)-1-Omega*x(2)];
    end
end

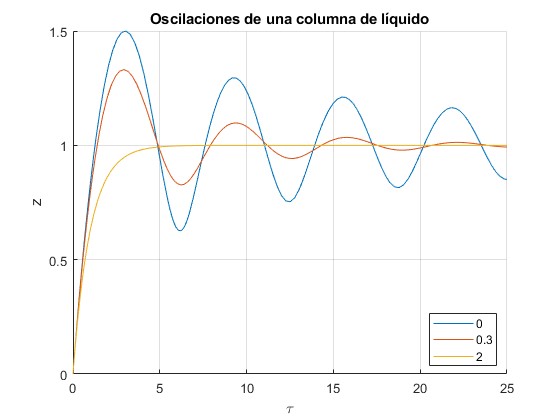
Cuando el parámetro Ω es grande, la altura de la columna de fluido tiene asintóticamente hacia el valor de equilibrio sin oscilar. Existe un valor crítico Ω_c para el cual la columna de líquido deja de oscilar. Un valor del parámetro Ω cercano a 0.3 describe aproximadamente las medidas efectuadas

tt=E0(9:end)-0.267;
zz=E2(9:end)/10;
h=10;
Omega=0.1550;
hold on
plot(tt,zz,'ko','markersize',3,'markerfacecolor','k')
[t,x]=ode45(@fL,[0,30],[0.02,0],[],Omega);
plot(t*sqrt(h/980),x(:,1)*h-h, 'b')   
hold off
grid on
ylabel('z (cm)')
xlabel('t (s)')
title('Oscilaciones de una columna de líquido')

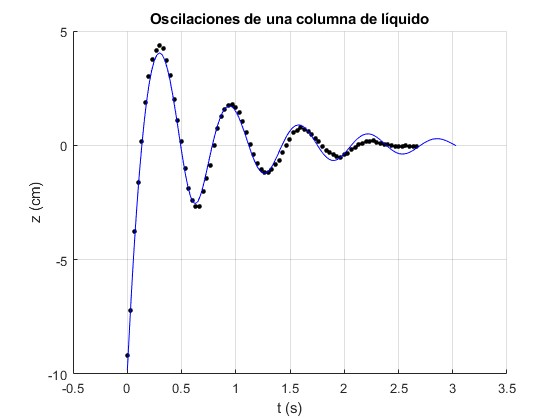
Este modelo describe algo mejor las medidas experimentales, al menos, en las primeras oscilaciones

Actividades

Se introduce

• El parámetro Ω

Se pulsa el botón titulado Nuevo

Se observa las oscilaciones de la columan de líquido una vez que se retira el dedo del extremos superior del tubo

Soluciones analíticas para Ω=0

Si el término disipativo dado por la ley de Poiseuille es despreciable (Ω=0) las ecuaciones del movimiento toman una forma más simple

${\displaystyle \{\begin{array}{l}\frac{d^{2}z}{d{\tau }^2}=\frac{1}{z}-1-\frac{1}{z}{\left(\frac{dz}{d\tau }\right)}^2,\frac{dz}{d\tau }>0\\ \frac{d^{2}z}{d{\tau }^2}=\frac{1}{z}-\mathrm{1,}\frac{dz}{d\tau }<0\end{array}}$

Teniendo en cuenta

${\displaystyle \frac{d^{2}z}{d{\tau }^2}=\frac{dv}{d\tau }=\frac{dv}{dz}\frac{dz}{d\tau }=v\frac{dv}{dz}=\frac{1}{2}\frac{d{v}^2}{dz}}$

• Primera ecuación, la columna de líquido asciende

La primera ecuación se escribe

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{d{v}^2}{dz}+\frac{v^2}{z}=\frac{1}{z}-1\\ z\frac{d{v}^2}{dz}+2v^2=2-2z\\ \frac{1}{z}\frac{d\left(z^2{v}^2\right)}{dz}=2-2z\\ d\left(z^2{v}^2\right)=\left(2z-2z^2\right)dz\end{array}}$

Integrando

${\displaystyle z^2{\left(\frac{dz}{d\tau }\right)}^2=z^2-\frac{2}{3}{z}^3+A}$

Donde A es la constante de integración

Si la columna de líquido parte z=0 en el instante τ=0, entonces A=0

Dividimos ambos miembros por z², obteniendo la ecuación diferencial

${\displaystyle {\left(\frac{dz}{d\tau }\right)}^2=1-\frac{2}{3}z}$

Integramos con la condición inicial, para τ=0, z=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{z}{\int }}\frac{dz}{\sqrt{1-\frac{2}{3}z}}={\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }}\\ -3\sqrt{1-\frac{2}{3}z}+3=\tau \\ \sqrt{1-\frac{2}{3}z}=1-\frac{\tau }{3}\\ z=\tau \left(1-\frac{\tau }{6}\right),0\le \tau \le 3\end{array}}$

El máximo se alcanza para τ=3 y vale z_max=1.5

• Segunda ecuación, la columna de líquido desciende

La segunda ecuación se escribe

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{d{v}^2}{dz}=\frac{1}{z}-1\\ \frac{1}{2}d{v}^2=\left(\frac{1}{z}-1\right)dz\end{array}}$

Integrando

${\displaystyle \frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^2=\ln z-z+B}$

Donde B es la constante de integración, que se obtiene sabiendo que z=z_max=1.5, dz/dτ=0

Para obtener la función z(τ) es necesario resolver numéricamente las dos ecuaciones diferenciales.

${\displaystyle \{\begin{array}{l}{z}^2{\left(\frac{dz}{d\tau }\right)}^2+\frac{2}{3}{z}^3-z^2=A,\frac{dz}{d\tau }>0\\ \frac{1}{2}{\left(\frac{dz}{d\tau }\right)}^2+z-\ln z=B,\frac{dz}{d\tau }>0\end{array}}$

Sin embargo, podemos obtener la sucesión de máximos z_max y mínimos z_min en los que dz/dt=0

${\displaystyle \{\begin{array}{l}\frac{2}{3}{z}_{\min }^3-z_{\min }^2=\frac{2}{3}{z}_{\max }^3-z_{\max }^2\\ z_{\min }-\ln z_{\min }=z_{\max }-\ln z_{\max }\end{array}}$

Empezamos con z_min=0, la primera ecuación 2z_max/3-z_min=0, z_max=3/2=1.5, valor ya calculado

En la segunda ecuación, z_min-lnz_min=1.5-ln1.5. Resolvemos esta ecuación transcendente para obtener z_min

Este código calcula la sucesión de máximos y mínimos, utilizando la función raices_3 que calcula las raíces de una ecuación cúbica. Alternativamnete, se puede utilizaar la función roots de MATLAB

function columna_liquido_4
    z_max=1.5;  
     %mínimo (menor que 1)
    for k=1:5
        f=@(x) x-log(x)-z_max+log(z_max);
        z_min=fzero(f,[0.1,1]);
        disp(z_min)
    %maximo (mayor que 1)
        raiz=raices_3([1, -3/2, 0, 3*z_min^2/2-z_min^3]);
        for i=1:3
            if raiz(i)>1
                break;
            end
        end
        z_max=raiz(i);
        disp(z_max)
    end

    function x = raices_3(p)
        Q=(p(2)*p(2)-3*p(3))/9;
        R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
        x=zeros(3,1); %reserva memoria para un vector de tres elementos
        if (R*R)<(Q^3)
            tetha=acos(R/sqrt(Q^3));
            x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
            x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
            x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
        else
            A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
            if A==0
                B=0;
            else
                B=Q/A;
            end
            x(1)=(A+B)-p(2)/3;
            x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); %mejor que i
            x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
        end
    end
end

z_max es mayor que 1 y z_min es menor. Siendo z=1, la altura de equilibrio

    0.6258
    1.2963
    0.7527
    1.2115
    0.8146
    1.1647
    0.8516
    1.1349
    0.8762
    1.1143

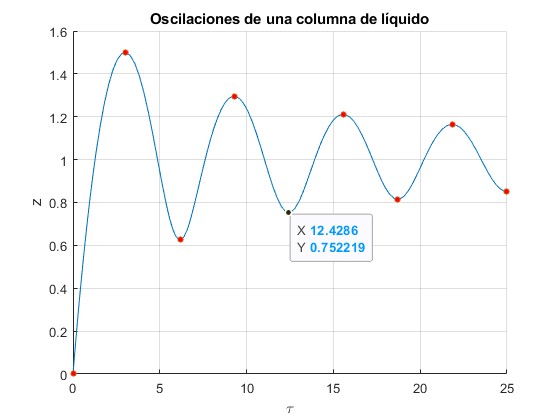
Resolvemos, empleando procedimientos numéricos, las dos ecuaciones diferenciales al principio de este apartado, señalamos los máximos y mínimos. Comprobamos pinchando con el cursor Data tips que su ordenada Y coincide con los valores calculados anteriormente

function columna_liquido_3  
    hold on
    opts=odeset('events',@columna_ode45);
    [t,x,te,xe]=ode45(@fL,[0,25],[0.001,0],opts);
    plot(t,x(:,1))
    plot(te,xe(:,1),'o','markersize',4,'markerfacecolor','r')
    hold off
    grid on
    xlabel('\tau')
    ylabel('z')
    title('Oscilaciones de una columna de líquido')

    function dif_2=fL(~,x)
            if x(2)>0
                dif_2=[x(2); 1/x(1)-1-x(2)^2/x(1)];
            else
                dif_2=[x(2); 1/x(1)-1];
            end
    end

    function [value,isterminal,direction]=columna_ode45(~,x)
        value=x(2); % velocidad
       isterminal=0;
        direction=0; 
    end
end

Referencias

Ryan P. Smith, Eric H. Matlis. Gravity-driven fluid oscillations in a drinking straw. Am. J. Phys. 87 (6) June 2019, pp. 433-435

David Quéré, Elie Raphaël. Rebounds in a Capillary Tube. Langmuir 1999, 15, pp. 3679-3682

Elise Lorenceau, David Quéré, Jean-Yves Ollitrault, Christophe Clanet. Gravitational oscillations of a liquid column in a pipe. Physics of Fluids, Volume 4, Number 6, June 2002, pp. 1985-1992