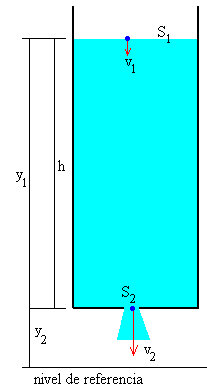
Un depósito cilíndrico, de sección S₁ tiene un orificio en el fondo de sección S₂ más pequeña que S₁. Aplicamos la ecuación de Bernoulli a los puntos (1) y (2) situados en la superficie libre del fluido y en el centro del orificio inferior.

${\displaystyle p_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2=p_2+\rho g{y}_2+\frac{1}{2}\rho v_2^2}$

El elemento de fluido delimitado por las secciones S₁ y S₂ está en contacto con el aire a la misma presión. Luego, p₁=p₂=p₀.

La diferencia de alturas es y₁-y₂=h. Siendo h la altura de la columna de fluido

Con estos datos la ecuación de Bernoulli se escribe

${\displaystyle \rho gh+\frac{1}{2}\rho v_1^2=\frac{1}{2}\rho v_2^2}$

La ecuación de continuidad se escribe

v₁S₁=v₂S₂

De estas dos ecuaciones obtenemos v₁ y v₂

${\displaystyle v_1=-\sqrt{\frac{2g}{\frac{S_1^2}{S_2^2}-1}h}=-\sqrt{\frac{2g}{\beta }h}}$

con

${\displaystyle v_1=\frac{dh}{dt}}$

Si la altura inicial del depósito en el instante t=0 es H. Integrando esta ecuación diferencial, obtenemos la expresión de la altura h en función del tiempo.

${\displaystyle \begin{array}{l}\frac{dh}{dt}=-\sqrt{\frac{2g}{\beta }h}\\ {\displaystyle \underset{H}{\overset{h}{\int }}\frac{dh}{\sqrt{h}}}=-\sqrt{\frac{2g}{\beta }}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \sqrt{H}-\sqrt{h}=\sqrt{\frac{g}{2\beta }}t\\ \frac{h}{H}={\left(1-\sqrt{\frac{g}{2\beta H}}t\right)}^2\end{array}}$

Cuando h=0, despejamos el tiempo t que tarda el depósito en vaciarse por completo.

${\displaystyle t=\sqrt{\left(\frac{S_1^2}{S_2^2}-1\right)\frac{2H}{g}}}$

Si el depósito es cilíndrico de radio R y el orificio es circular de radio r

${\displaystyle t=\sqrt{\left(\frac{R^4}{r^4}-1\right)\frac{2H}{g}}}$

Si R>>r, se puede despreciar la unidad

${\displaystyle t\approx \frac{R^2}{r^2}\sqrt{\frac{2H}{g}}}$

Ejemplo.

• Radio del depósito 10 cm, luego, S₁=π (0.1)² m²
• Radio del orificio 0.8 cm, luego, S₂=π(0.008)² m²
• Altura inicial 45 cm, H=0.45 m

Sustituyendo estos datos en la fórmula del tiempo obtenemos t=47.34 s, que es el tiempo que tarda en vaciarse completamente el depósito. Si aplicamos la aproximación S₁>>S₂, obtenemos prácticamente el mismo tiempo t=47.35 s.

S1=pi*0.1^2;  %sección del depósito
S2=pi*0.008^2; %sección del orificio
H=0.45; %altura inicial del fluido
tMax=sqrt(2*H*(S1^2/S2^2-1)/9.8); %tiempo que tarda en salir el fluido
t=linspace(0,tMax,100);
h=(sqrt(H)-S2*sqrt(2*9.8/(S1^2-S2^2))*t/2).^2;
plot(t,h)
grid on
xlabel('t(s)')
ylabel('h(m)')
title('Vaciado de un depósito')

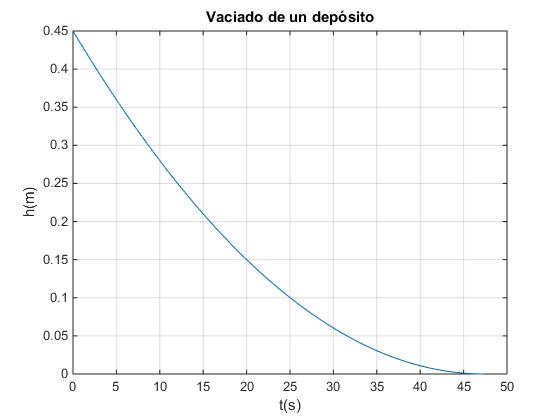
tMax =   47.3499

Actividades

Se introduce:

• el radio del depósito R₁, en el control titulado Radio depósito
• el radio del orificio R₂ situado en el fondo, en el control titulado Radio del orificio
• la altura inicial H de agua en el depósito, se ha fijado en 45 cm.

Se pulsa en el botón titulado Nuevo

El fluido comienza a salir por el orificio, a la vez que se representa gráficamente la altura de la columna de fluido en función del tiempo.

Estado no estacionario

El flujo Q no es constante, por lo que aplicamos aplicamos la ecuación de Bernoulli en el estado no estacionario a los puntos (1) y (2) situados en la superficie libre del fluido y en el centro del orificio inferior

${\displaystyle \begin{array}{l}\left(p_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2\right)-\left(p_2+\rho g{y}_2+\frac{1}{2}\rho v_2^2\right)=\frac{dQ}{dt}{\displaystyle \underset{1}{\overset{2}{\int }}\frac{ds}{A(s)}}\\ Q=\frac{dm}{dt}=\rho Av=\rho S_1{v}_1=\rho S_2{v}_2\end{array}}$

El resultado es una ecuación diferencial en h

${\displaystyle \begin{array}{l}{v}_1=\frac{dh}{dt},v_2=\frac{S_1}{S_2}\frac{dh}{dt},\frac{d{v}_1}{dt}=\frac{d^{2}h}{d{t}^2},{\displaystyle \underset{h}{\overset{0}{\int }}\frac{ds}{A(s)}=-\frac{h}{S_1}}\hfill \\ \left(p_0+\rho g{y}_1+\frac{1}{2}\rho {\left(\frac{dh}{dt}\right)}^2\right)-\left(p_0+\rho g{y}_2+\frac{1}{2}\rho {\left(\frac{S_1}{S_2}\frac{dh}{dt}\right)}^2\right)=-\rho S_1\frac{d^{2}h}{d{t}^2}\frac{h}{S_1}\hfill \\ h\left(\frac{d^{2}h}{d{t}^2}+g\right)-\frac{1}{2}\left(\frac{S_1^2}{S_2^2}-1\right){\left(\frac{dh}{dt}\right)}^2=0\hfill \\ h\left(\frac{d^{2}h}{d{t}^2}+g\right)-\frac{1}{2}\beta {\left(\frac{dh}{dt}\right)}^2=\mathrm{0,}\beta =\frac{S_1^2}{S_2^2}-1\hfill \end{array}}$

Se resuelve esta ecuación diferencial con las condiciones iniciales siguientes, en el instante t=0, h=H y dh/dt=0.

Si el vaciado del depósito es lento se puede despreciar la aceleración d²h/dt² frente a la aceleración de la gravedad g

${\displaystyle \begin{array}{l}hg\approx \frac{1}{2}\beta {\left(\frac{dh}{dt}\right)}^2\\ \frac{dh}{dt}\approx -\sqrt{\frac{2g}{\beta }h}\end{array}}$

Se toma la raíz negativa ya que h disminuye con el tiempo t. Tenemos la ecuación diferencial correspondiente al estado estacionario, cuya solución es

${\displaystyle \frac{h}{H}={\left(1-\sqrt{\frac{g}{2\beta H}}t\right)}^2}$

Es conveniente, expresar las ecuaciones en términos de magnitudes adimensionales z y τ

${\displaystyle \begin{array}{l}z=\frac{h}{H},\tau =\sqrt{\frac{g}{2\beta H}}t\\ z={\left(1-\tau \right)}^2\end{array}}$

El depósito se vacía z=0, en el instante τ=1

La ecuación diferencial en h se expresa en términos de las magnitudes adimensionales z y τ

${\displaystyle 2z\frac{d^{2}z}{d{\tau }^2}-\beta {\left(\frac{dz}{d\tau }\right)}^2+4\beta z=0}$

Que se resolverá mediante procedimientos numéricos, con las siguientes condiciones iniciales, en el instante τ=0, z=1, dz/dτ=0

Para β=3, $\frac{R}{r}=\sqrt{2}$ , el tiempo adimensional de vaciado z=0, es el instante τ=1.07, mientras que el tiempo aproximado es τ=1

function vaciado
    beta=3;
    opts=odeset('events',@stop_vaciado);
    f=@(t,x)[x(2); beta*x(2)^2/(2*x(1))-2*beta];
    [t,x]=ode45(f,[0,10],[1,0],opts);
    hold on
    plot(t,x(:,1))
    fplot(@(t) (1-t).^2,[0,1])
    disp(t(end))
    grid on
    legend('Exacto','Aproximado','Location','best')
    xlabel('\tau')
    ylabel('z');
    title('Vaciado de un depósito')

    function [value,isterminal,direction]=stop_vaciado(~,x)
        value=x(1);
        isterminal=1;    
        direction=-1; 
    end
end

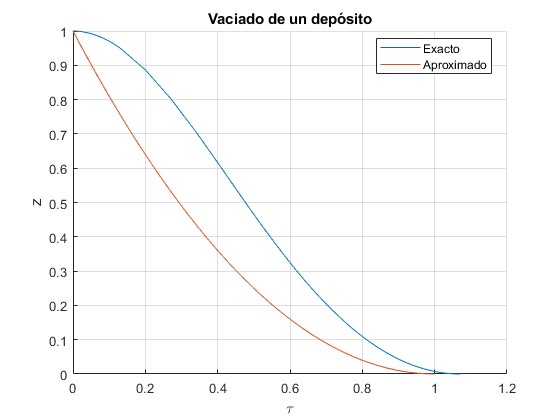
    1.0704

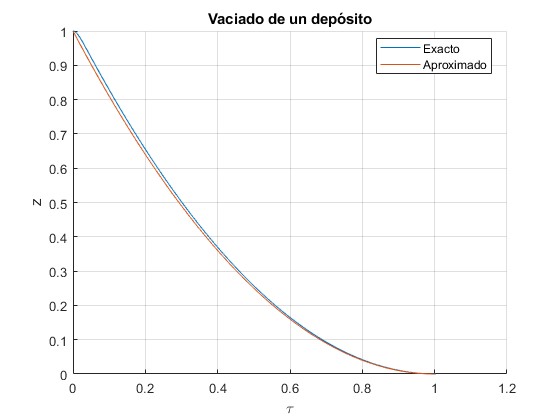
En la mayor parte de los casos R>>r, por lo que β>>1. Por ejemplo, para β=63, $\frac{R}{r}=2\sqrt{2}$ hay poca diferencia entre ambas soluciones

Experiencia

Se han medido las alturas de líquido y tiempos en un depósito cilíndrico transparente inicialmente lleno hasta una altura H=1 m. El depósito tiene un orificio en la parte inferior que se abre en el instante t=0

Representamos los datos y los ajustamos a la función h(t)/H=At²+Bt+C

h=0.8:-0.1:0.1; %alturas del líquido
t=[6.8,14.2,22.2,30.7,40.4,51.0,63.8,80.3]; 
plot(t,h,'ro','markersize',4,'markerfacecolor','r') %tiempos
grid on
xlim([0,115])
xlabel('t(s)')
ylabel('h/H')
title('Vaciado de un depósito')

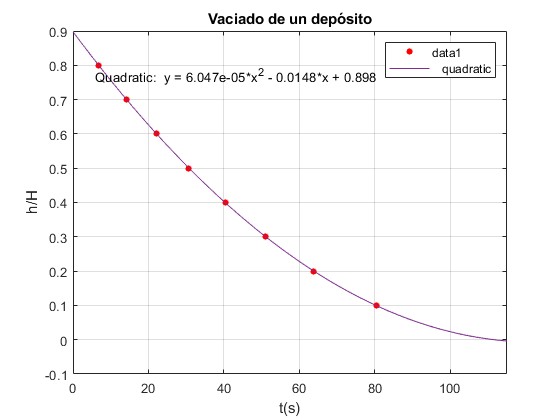
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla Quadatic en Types of fits.

Vemos que los datos experimentales se ajustan a dicha función, con A=6.047·10^-5, B=-0.0148, C=0.898

El depósito se vacía completamente, h=0, en el instante t_f=111 s, como apreciamos en la gráfica

${\displaystyle t_f=\frac{-B-\sqrt{B^2-4AC}}{2A}}$

>> A=6.047e-5; B=-0.0148; C=0.898;
>> (-B-sqrt(B^2-4*A*C))/(2*A)
ans =  111.1838

Solución analítica

Buscamos una solución analítica a la ecuación diferencial

${\displaystyle 2z\frac{d^{2}z}{d{\tau }^2}-\beta {\left(\frac{dz}{d\tau }\right)}^2+4\beta z=0}$

Con las siguientes condiciones iniciales, en el instante τ=0, z=1, dz/dτ=0

Cambiamos la variable tiempo τ a desplazamiento z, obteniendo la ecuación diferencial de primer orden

${\displaystyle \begin{array}{l}V=\frac{dz}{d\tau }\\ 2\frac{dV}{d\tau }-\beta \frac{V^2}{z}+4\beta =0\\ \frac{dV}{d\tau }=\frac{dV}{dz}\frac{dz}{d\tau }=V\frac{dV}{dz}=\frac{1}{2}\frac{d{V}^2}{dz}\\ \frac{d{V}^2}{dz}-\beta \frac{V^2}{z}+4\beta =0\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}\eta =\frac{V^2}{z},\\ \frac{d\eta }{dz}=\frac{\frac{d{V}^2}{dz}z-V^2}{z^2}=\frac{\left(\beta \frac{V^2}{z}-4\beta \right)z-V^2}{z^2}=\frac{\left(\beta -1\right)V^2-4\beta z}{z^2}\end{array}}$

• Para β≠1

Separando las variables, integramos

${\displaystyle \begin{array}{l}\frac{d\eta }{dz}=\frac{\left(\beta -1\right)\eta -4\beta }{z}\\ {\displaystyle \int \frac{d\eta }{\left(\beta -1\right)\eta -4\beta }={\displaystyle \int \frac{dz}{z}}}\\ \frac{1}{\left(\beta -1\right)}\ln \left(\left(\beta -1\right)\eta -4\beta \right)=\ln z+c\\ \left(\beta -1\right)\eta -4\beta =c{z}^{\beta -1}\end{array}}$

Las condiciones iniciales determinan la constante de integración c

${\displaystyle \begin{array}{l}c=-4\beta \\ \eta =\frac{4\beta }{\beta -1}\left(1-z^{\beta -1}\right)\\ V^2=\frac{4\beta }{\beta -1}z\left(1-z^{\beta -1}\right)\end{array}}$

La altura de fluido z=h/H es (tomamos la raíz negativa)

${\displaystyle \begin{array}{l}\frac{dz}{d\tau }=-2\sqrt{\frac{\beta }{\beta -1}}\sqrt{z\left(1-z^{\beta -1}\right)}\\ {\displaystyle \underset{1}{\overset{z}{\int }}\frac{dz}{\sqrt{z\left(1-z^{\beta -1}\right)}}}=-2\sqrt{\frac{\beta }{\beta -1}}{\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }\\ {\displaystyle \underset{1}{\overset{z}{\int }}\frac{dz}{\sqrt{z\left(1-z^{\beta -1}\right)}}}=-2\sqrt{\frac{\beta }{\beta -1}}\tau \end{array}}$

El tiempo de descarga desde z=1 a z=0, es

${\displaystyle \begin{array}{l}{\displaystyle \underset{1}{\overset{0}{\int }}\frac{dz}{\sqrt{z\left(1-z^{\beta -1}\right)}}}=-2\sqrt{\frac{\beta }{\beta -1}}{\rm T}\\ {\rm T}=\frac{1}{2}\sqrt{\frac{\beta -1}{\beta }}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{dz}{\sqrt{z\left(1-z^{\beta -1}\right)}}}\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}t=z^{\beta -1},\sqrt{z}=t^{\frac{1}{2\left(\beta -1\right)}},dt=\left(\beta -1\right)z^{\beta -2}dz=\left(\beta -1\right)\frac{t}{t^{\frac{1}{\beta -1}}}dz\\ T=\frac{1}{2}\sqrt{\frac{\beta -1}{\beta }}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{t^{\frac{1}{\beta -1}}}{\left(\beta -1\right)t}\frac{dt}{t^{\frac{1}{2\left(\beta -1\right)}}\sqrt{1-t}}}=\frac{1}{2}\sqrt{\frac{1}{\left(\beta -1\right)\beta }}{\displaystyle \underset{0}{\overset{1}{\int }}{t}^{\frac{1}{2\left(\beta -1\right)}-1}{\left(1-t\right)}^{-1/2}dt}\end{array}}$

Expresamos la integral en términos de la función beta

${\displaystyle \begin{array}{l}m=\frac{1}{2\left(\beta -1\right)}-\mathrm{1,}n=-\frac{1}{2}\\ T=\frac{1}{2}\sqrt{\frac{1}{\left(\beta -1\right)\beta }}\frac{\Gamma \left(\frac{1}{2\left(\beta -1\right)}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{1}{2\left(\beta -1\right)}+\frac{1}{2}\right)}=\frac{1}{2}\sqrt{\frac{\pi }{\left(\beta -1\right)\beta }}\frac{\Gamma \left(\frac{1}{2\left(\beta -1\right)}\right)}{\Gamma \left(\frac{1}{2\left(\beta -1\right)}+\frac{1}{2}\right)}\end{array}}$

Representamos la velocidad V del fluido en función de la altura z=h/H. Resolvemos la ecuación diferencial por procedimientos numéricos y la comparamos con la solución analítica. Comparamos el tiempo que tarda en vaciarse el depósito por ambos procedimientos

function descarga_2
    beta=3;
    opts=odeset('events',@stop_vaciado);
    f=@(t,x)[x(2); beta*x(2)^2/(2*x(1))-2*beta];
    [t,x]=ode45(f,[0,10],[1,0],opts);
    hold on
    plot(x(:,1),x(:,2))
    V=@(z) -2*sqrt(beta*z.*(1-z.^(beta-1))/(beta-1));
    fplot(V,[0,1])
    T=sqrt(pi/(beta*(beta-1)))*gamma(1/(2*(beta-1)))
/(2*gamma(1/(2*(beta-1))+1/2));
    disp([t(end),T])
    hold off
    grid on
    legend('Numérico','Exacto','Location','best')
    xlabel('z')
    ylabel('V');
    title('Vaciado de un depósito')

    function [value,isterminal,direction]=stop_vaciado(~,x)
        value=x(1);
        isterminal=1;    
        direction=-1; 
    end
end



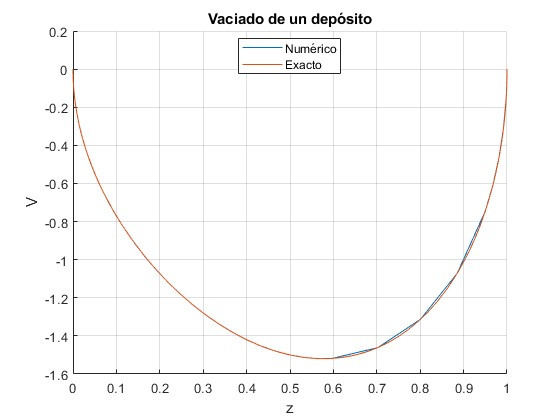
Los tiempos de vaciado coinciden

   1.0704    1.0705

Cambiamos β=20



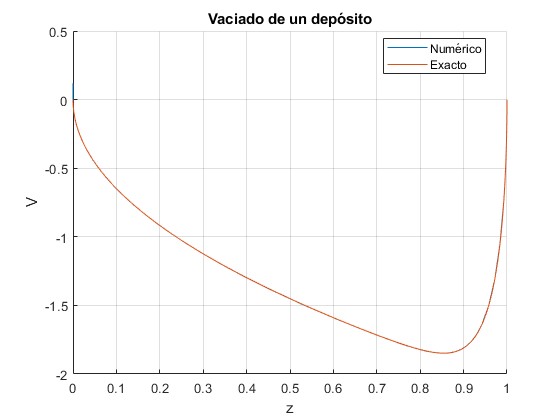
1.0098    1.0098

• Para β=1

${\displaystyle \begin{array}{l}\frac{d\eta }{dz}=-\frac{4}{z}\\ \eta =-4\ln z+c\end{array}}$

Las condiciones iniciales determinan la constante de integración c

${\displaystyle \begin{array}{l}c=0\\ \eta =-4\ln z\\ V^2=-4z\ln z\end{array}}$

El resultado es un número positivo, ya que ln(z)<0 para z<1

La altura de fluido z=h/H es

${\displaystyle \begin{array}{l}\frac{dz}{d\tau }=2\sqrt{-z\ln z}\\ {\displaystyle \underset{1}{\overset{z}{\int }}\frac{dz}{\sqrt{-z\ln z}}}=2{\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }\\ {\displaystyle \underset{1}{\overset{z}{\int }}\frac{dz}{\sqrt{-z\ln z}}}=2\tau \end{array}}$

El tiempo de descarga desde z=1 a z=0, es

${\displaystyle \begin{array}{l}{\rm T}=-\frac{1}{2}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{dz}{\sqrt{-z\ln z}}}\\ u=\sqrt{\ln \left(\frac{1}{z}\right)},du=-\frac{dz}{2z\sqrt{\ln \left(\frac{1}{z}\right)}}=-\frac{dz}{2zu}\\ u=\sqrt{-\ln z},z=e^{-u^2}\\ {\displaystyle \int \frac{dz}{\sqrt{z\ln \left(\frac{1}{z}\right)}}=}{\displaystyle \int \frac{-2zu·du}{\sqrt{z}u}}=-2{\displaystyle \int \sqrt{z}}du=-2{\displaystyle \int e^{-u^2/2}}du\\ {\rm T}={\displaystyle \underset{-\infty }{\overset{0}{\int }}{e}^{-u^2/2}du}\end{array}}$

Teniendo en cuenta el resultado de la integral

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\frac{x^2}{2}\right)dx}=\sqrt{\frac{\pi }{2}}\\ {\rm T}=\sqrt{\frac{\pi }{2}}\end{array}}$

>> syms x;
>> y=exp(-x^2/2);
>> int(y,x,0,inf)
ans =(2^(1/2)*pi^(1/2))/2

Representamos la velocidad V del fluido en función de la altura z=h/H. Resolvemos la ecuación diferencial por procedimientos numéricos y la comparamos con la solución analítica. Comparamos el tiempo que tarda en vaciarse el depósito por ambos procedimientos

function descarga_3
    beta=1;
    opts=odeset('events',@stop_vaciado);
    f=@(t,x)[x(2); beta*x(2)^2/(2*x(1))-2*beta];
    [t,x]=ode45(f,[0,10],[1,0],opts);
    hold on
    plot(x(:,1),x(:,2))
    V=@(x) -2*sqrt(-x.*log(x));
    fplot(V,[0,1])
    disp([t(end),sqrt(pi/2)])
    hold off
    grid on
    legend('Numérico','Exacto','Location','best')
    xlabel('z')
    ylabel('V');
    title('Vaciado de un depósito')

    function [value,isterminal,direction]=stop_vaciado(~,x)
        value=x(1);
        isterminal=1;    
        direction=-1; 
    end
end



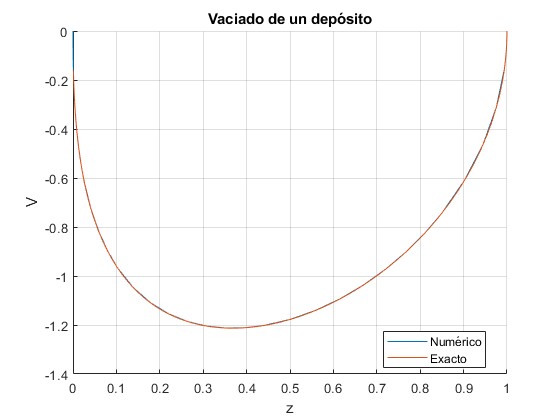
Los tiempos de vaciado coinciden

  1.2531    1.2533

Balance energético

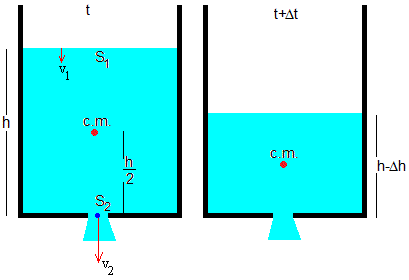
• Variación de energía potencial

En el instante t, la energía potencial del líquido contenido en el depósito es

${\displaystyle E_1=\left(\rho S_{1}h\right)g\frac{h}{2}=\rho S_{1}g\frac{h^2}{2}}$

En el instante t+Δt, la energía potencial del líquido contenido en el depósito es

${\displaystyle E_2=\left(\rho S_1\left(h-\Delta h\right)\right)g\frac{h-\Delta h}{2}=\rho S_{1}g\frac{{\left(h-\Delta h\right)}^2}{2}}$

La variación de energía potencial es

${\displaystyle \Delta E_p=E_2-E_1=\rho S_{1}g\left(-h+\frac{\Delta h}{2}\right)\Delta h}$

En el límite cuando Δt→0

${\displaystyle \frac{d{E}_p}{dt}=-\rho S_{1}gh\frac{dh}{dt}}$

• La energía cinética del líquido contenido en el depósito es

${\displaystyle E_{k1}=\frac{1}{2}\left(\rho S_{1}h\right)v_1^2=\frac{1}{2}\left(\rho S_{1}h\right){\left(-\frac{dh}{dt}\right)}^2}$

Su variación con el tiempo es

${\displaystyle \frac{d{E}_{k1}}{dt}=\frac{1}{2}\left(\rho S_1\right){\left(\frac{dh}{dt}\right)}^3+\left(\rho S_{1}h\right)\frac{dh}{dt}\frac{d^{2}h}{d{t}^2}}$

• Energía cinética del líquido que sale por el orificio

Por el orificio sale una masa dm=ρS₂v₂ de líquido en un intervalo de tiempo dt. La variación de energía cinética con el tiempo es

${\displaystyle \frac{d{E}_{k2}}{dt}=\frac{1}{2}\frac{dm}{dt}{v}_2^2=\frac{1}{2}\left(\rho S_2{v}_2\right)v_2^2=\frac{1}{2}\rho \frac{S_1^3}{S_2^2}{v}_1^3=-\frac{1}{2}\rho \frac{S_1^3}{S_2^2}{\left(\frac{dh}{dt}\right)}^3}$

La conservación de la energía implica que

${\displaystyle \begin{array}{l}\frac{d{E}_p}{dt}=\frac{d{E}_{k1}}{dt}+\frac{d{E}_{k2}}{dt}\\ -\rho S_{1}gh\frac{dh}{dt}=\frac{1}{2}\left(\rho S_1\right){\left(\frac{dh}{dt}\right)}^3+\left(\rho S_{1}h\right)\frac{dh}{dt}\frac{d^{2}h}{d{t}^2}-\frac{1}{2}\rho \frac{S_1^3}{S_2^2}{\left(\frac{dh}{dt}\right)}^3\\ -gh=\frac{1}{2}{\left(\frac{dh}{dt}\right)}^2+h\frac{d^{2}h}{d{t}^2}-\frac{1}{2}\frac{S_1^2}{S_2^2}{\left(\frac{dh}{dt}\right)}^2\\ h\left(g+\frac{d^{2}h}{d{t}^2}\right)-\frac{1}{2}\left(\frac{S_1^2}{S_2^2}-1\right){\left(\frac{dh}{dt}\right)}^2=0\\ h\left(g+\frac{d^{2}h}{d{t}^2}\right)-\frac{1}{2}\beta {\left(\frac{dh}{dt}\right)}^2=0\end{array}}$

La misma ecuación diferencial que la obtenida a partir de la ecuación de Bernoulli en el estado no estacionario

Referencias

Njock J, Mechanics of the slow draining of a large tank under gravity. Am. J. Phys. 71 (11) November 2003, pp. 1204-1207

M Blasone, F Dell’Anno, R De Luca, O Faella, O Fiore, A Saggese. Discharge time of a cylindrical leaking bucket. Eur. J. Phys. 36 (2015) 035017

Chris Geeter, Richard Huynh, Sebastian M. Marotta. One-Dimensional Unsteady Flow From A Cylindrical Draining Tank. October 30, 2018.

Johann Otto, Kirk T. McDonald. Torricelli’s Law for Large Holes. September 2018