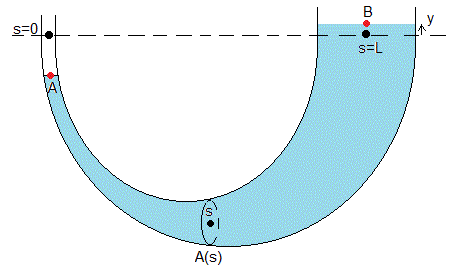
En la figura, se muestra un tubo de sección variable A(s) que contiene líquido. La línea a trazos señala la situación de equilibrio. Trazamos el eje del tubo y designamos s=0, el punto de color negro situado en el brazo izquierdo, intersección de la línea a trazos con el eje, y s=L el punto de color negro situado en el brazo derecho, intersección de la línea a trazos con dicho eje

En un instante dado t, la superficie libre del líquido en el brazo iquierdo se encuentra en A y en el brazo derecho en B. Como el líquido se supone incompresible, se cumplirá que

${\displaystyle {\displaystyle \underset{0}{\overset{s_A}{\int }}A(s)·ds={\displaystyle \underset{L}{\overset{s_B}{\int }}A(s)·ds}}}$

Con s_B=L+y, siendo y la posición de B respecto del nivel de equilibrio (línea a trazos). El punto A se encuentra s_A por debajo del nivel de equilibrio

Energías

• Energía potencial



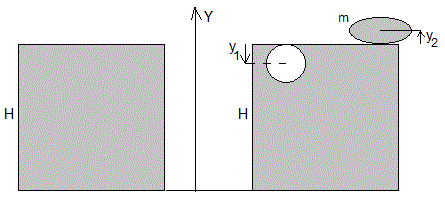
Supongamos una pieza en posición vertical, se recorta una porción de masa m cuyo centro de masas está en y₁ y se desplaza a la parte superior derecha, estando su centro de masas en y₂, el cambio de energía potencial es E_p=mg(H+y₂)-mg(H-y₁)= mgy₂+mgy₁

Lo mismo sucede para la porción de líquido que se desplaza desde el brazo izquierdo al derecho

${\displaystyle E_p={\displaystyle \underset{L}{\overset{s_B}{\int }}\left(s-L\right)}\rho g·A(s)·ds+{\displaystyle \underset{0}{\overset{s_A}{\int }}s\rho g·A(s)·ds}}$

• Energía cinética

${\displaystyle E_k={\displaystyle \underset{s_A}{\overset{s_B}{\int }}\left(\frac{1}{2}\rho v^2\right)}A(s)·ds=\frac{1}{2}\rho A^2(s_B)v_B^2{\displaystyle \underset{s_A}{\overset{s_B}{\int }}\frac{ds}{A(s)}}}$

Donde hemos empleado la ecuación de continuidad

${\displaystyle v(s)A(s)=A(s_B)v_B}$

Ecuación del movimiento

Como la energía total permenece constante, la derivada con respecto del tiempo, será cero

${\displaystyle \frac{d}{dt}\left(E_k+E_p\right)=0}$

La regla de Leibniz para calcular la derivada de una integral en el que el integrando y los límites varían con el tiempo es

${\displaystyle \frac{d}{dt}{\displaystyle \underset{a(t)}{\overset{b(t)}{\int }}f(x,t)dx=f(b,t)\frac{db}{dt}}-f(a,t)\frac{da}{dt}+{\displaystyle \underset{a}{\overset{b}{\int }}\frac{\partial f}{\partial t}}dx}$

• Energía potencial

En la expresión de la energía potencial, el integrando f(x,t) no depende explícitamente del tiempo, el último término es nulo. Por otra parte, el límite inferior a es constante da/dt=0, solamente hay que evaluar el primer término f(b,t)db/dt

${\displaystyle \frac{d{E}_p}{dt}=\left(s_B-L\right)\rho gA(s_B)v_B+s_A\rho gA(s_A)v_A=\rho g\left(s_B-L+s_A\right)A(s_B)v_B}$

Se ha tenido en cuenta la ecuación de continuidad, $A(s_B)v_B=A(s_A)v_A$

• Energía cinética

Para la energía cinética, f(x,t) no depende explícitamente de t y por tanto, el último término es nulo, queda evaluar la diferencia de dos términos f(b,t)db/dt-f(a,t)da/dt. Por otra parte, en la energía cinética tenemos la derivada de un producto de tres términos

${\displaystyle \begin{array}{l}\frac{d{E}_k}{dt}=\frac{1}{2}\rho ·A^2(s_B)·v_B^2\left\{\frac{1}{A(s_B)}{v}_B-\frac{1}{A(s_A)}{v}_A\right\}+\rho \left\{A(s_B){\left(\frac{dA(s)}{dt}\right)}_B{v}_B^2+A^2(s_B)·v_B\frac{d{v}_B}{dt}\right\}{\displaystyle \underset{s_A}{\overset{s_B}{\int }}\frac{ds}{A(s)}}=\\ \frac{1}{2}\rho ·A^2(s_B)·v_B^2\left\{\frac{1}{A(s_B)}{v}_B-\frac{A(s_B)}{A^2(s_A)}{v}_B\right\}+\rho \left\{A(s_B){\left(\frac{dA(s)}{ds}\right)}_B{v}_B^3+A^2(s_B)·v_B\frac{d{v}_B}{dt}\right\}{\displaystyle \underset{s_A}{\overset{s_B}{\int }}\frac{ds}{A(s)}}\end{array}}$

Sumamos ambas contribuciones

${\displaystyle \frac{1}{2}\rho A^2(s_B)v_B^2\left\{\frac{1}{A(s_B)}{v}_B-\frac{A(s_B)}{A^2(s_A)}{v}_B\right\}+\rho \left\{A(s_B){\left(\frac{dA(s)}{ds}\right)}_B{v}_B^3+A^2(s_B)v_B\frac{d{v}_B}{dt}\right\}{\displaystyle \underset{s_A}{\overset{s_B}{\int }}\frac{ds}{A(s)}}+\rho g\left(s_B-L+s_A\right)A(s_B)v_B=0}$

Dividimos por ρA(s_B)v_B

${\displaystyle \frac{1}{2}{v}_B^2\left\{1-\frac{A^2(s_B)}{A^2(s_A)}\right\}+\left\{{\left(\frac{dA(s)}{ds}\right)}_B{v}_B^2+A(s_B)\frac{d{v}_B}{dt}\right\}{\displaystyle \underset{s_A}{\overset{s_B}{\int }}\frac{ds}{A(s)}}+g\left(s_B-L+s_A\right)=0}$

Teniendo en cuenta que s_B=L+y, y v_B=dy/dt, obtenemos la ecuación diferencial del movimiento

${\displaystyle \frac{1}{2}{\left(\frac{dy}{dt}\right)}^2\left\{1-\frac{A^2(L+y)}{A^2(s_A)}\right\}+\left\{{\left(\frac{dA(s)}{ds}\right)}_{L+y}{\left(\frac{dy}{dt}\right)}^2+A(L+y)\frac{d^{2}y}{d{t}^2}\right\}{\displaystyle \underset{s_A}{\overset{L+y}{\int }}\frac{ds}{A(s)}}+g\left(y+s_A\right)=0}$

La forma del tubo A(s) estabecerá la relación entre las variables s_A e y, las expresiones de la derivada de A(s) en L+y y de la integral definida

Tubo de sección constante

El caso más simple es un tubo de sección constante A(s)=A. Al ser el fluido imcompresible, s_A=s_B-L=y. La ecuación del movimiento se reduce a

${\displaystyle \begin{array}{l}\left\{A\frac{d^{2}y}{d{t}^2}\right\}\frac{L}{A}+g\left(y+s_A\right)=0\\ \frac{d^{2}y}{d{t}^2}+2\frac{g}{L}y=0\end{array}}$

Tubo de sección variable

Consideremos un tubo de sección variable cuyo radio viene dado por la fórmula r=(s+r₀)k. El área de la sección en la posición s a lo largo del eje del tubo es $A(s)=\pi \left(s+r_0\right)k^2$

Para s=0, el radio es r=r₀k y para s=L, r=(L+r₀)k

Para un fluido incompresible

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{s_A}{\int }}\pi {\left(s+r_0\right)}^2·k^2·ds={\displaystyle \underset{L}{\overset{s_B}{\int }}\pi {\left(s+r_0\right)}^2·k^2·ds}}\\ {\displaystyle \underset{0}{\overset{s_A}{\int }}\left(s^2+r_0^2+2s{r}_0\right)·ds={\displaystyle \underset{L}{\overset{s_B}{\int }}\left(s^2+r_0^2+2s{r}_0\right)·ds}}\\ \frac{s_A^3}{3}+r_0^2{s}_A+r_0{s}_A^2=\frac{s_B^3}{3}+r_0^2{s}_B+r_0{s}_B^2-\frac{L^3}{3}-r_0^{2}L-r_0{L}^2\end{array}}$

Sabiendo que s_B=L+y, establecemos la relación entre s_A e y

${\displaystyle s_A^3+3r_0{s}_A^2+3r_0^2{s}_A-{\left(y+L+r_0\right)}^3+{\left(L+r_0\right)}^3=0}$

Obtenemos la raíz real de esta ecuación cúbica

${\displaystyle \begin{array}{l}a=3r_0,b=3r_0^2,c=-{\left(y+L+r_0\right)}^3+{\left(L+r_0\right)}^3\\ P=b-\frac{a^2}{3}=0\\ Q=\frac{ab}{3}-c-\frac{2}{27}{a}^3=r_0^3+{\left(y+L+r_0\right)}^3-{\left(L+r_0\right)}^3\\ v^3=-Q,u=0\\ s_A=(u-v)-\frac{a}{3}={\left(r_0^3+{\left(y+L+r_0\right)}^3-{\left(L+r_0\right)}^3\right)}^{1/3}-r_0\end{array}}$

Para resolver la ecuación diferencial del movimiento nos falta la expresión de la derivada de A(s) evaluada en L+y

${\displaystyle {\left(\frac{dA(s)}{ds}\right)}_{L+y}=2\pi \left(L+y+r_0\right)k^2}$

y la integral definida

${\displaystyle {\displaystyle \underset{s_A}{\overset{L+y}{\int }}\frac{ds}{A(s)}}={\displaystyle \underset{s_A}{\overset{L+y}{\int }}\frac{ds}{\pi {\left(s+r_0\right)}^2{k}^2}=\frac{1}{\pi k^2}}{\frac{{\left(s+r_0\right)}^{-1}}{-1}|}_{s_A}^{L+y}=\frac{1}{\pi k^2}\left\{\frac{1}{s_A+r_0}-\frac{1}{L+y+r_0}\right\}}$

La ecuación diferencial del movimiento se transforma en

${\displaystyle \begin{array}{l}\frac{1}{2}{\left(\frac{dy}{dt}\right)}^2\left\{1-\frac{A^2(L+y)}{A^2(s_A)}\right\}+\left\{2\pi \left(L+y+r_0\right)k^2{\left(\frac{dy}{dt}\right)}^2+A(L+y)·\frac{d^{2}y}{d{t}^2}\right\}\frac{1}{\pi k^2}\left\{\frac{1}{s_A+r_0}-\frac{1}{L+y+r_0}\right\}+g\left(y+s_A\right)=0\\ \left\{\frac{1}{2}\left(1-\frac{A^2(L+y)}{A^2(s_A)}\right)+2\left(\frac{L+y+r_0}{s_A+r_0}-1\right)\right\}{\left(\frac{dy}{dt}\right)}^2+\frac{A(L+y)}{\pi k^2}\left\{\frac{1}{s_A+r_0}-\frac{1}{L+y+r_0}\right\}\frac{d^{2}y}{d{t}^2}+g\left(y+s_A\right)=0\end{array}}$

que junto a la relación entre s_A e y resolveremos por el procedimiento numérico ode45 de MATLAB

Conservación de la energía

Una forma de verificar la solución de la ecuación del movimiento es la de comprobar si la energía se mantiene aproximadamente constante

• Energía potencial

${\displaystyle \begin{array}{l}{E}_p={\displaystyle \underset{L}{\overset{s_B}{\int }}\left(s-L\right)}\rho gA(s)·ds+{\displaystyle \underset{0}{\overset{s_A}{\int }}s\rho gA(s)·ds}=\\ \rho g\pi k^2\left\{{\displaystyle \underset{L}{\overset{s_B}{\int }}\left(s-L\right)}{\left(s+r_0\right)}^{2}ds+{\displaystyle \underset{0}{\overset{s_A}{\int }}s{\left(s+r_0\right)}^{2}ds}\right\}=\\ \rho g\pi k^2\left\{{\displaystyle \underset{L}{\overset{L+y}{\int }}\left(s^3+\left(2r_0-L\right)s^2+2r_0\left(r_0-L\right)s-L{r}_0^2\right)}ds+{\displaystyle \underset{0}{\overset{s_A}{\int }}\left(s^3+2r_0{s}^2+r_0^{2}s\right)ds}\right\}=\\ \rho g\pi k^2\left\{\frac{{\left(L+y\right)}^4}{4}-\frac{L^4}{4}+\left(2r_0-L\right)\left(\frac{{\left(L+y\right)}^3}{3}-\frac{L^3}{3}\right)+r_0\left(r_0-2L\right)\left(\frac{{\left(L+y\right)}^2}{2}-\frac{L^2}{2}\right)-L{r}_0^{2}y+\frac{s_A^4}{4}+2r_0\frac{s_A^3}{3}+r_0^2\frac{s_A^2}{2}\right\}\end{array}}$

• Energía cinética

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}\rho A^2(s_B)v_B^2{\displaystyle \underset{s_A}{\overset{s_B}{\int }}\frac{ds}{A(s)}}=\frac{1}{2}\rho ·{\pi }^2{\left(L+y+r_0\right)}^4{k}^4·v_B^2{\displaystyle \underset{s_A}{\overset{L+y}{\int }}\frac{ds}{\pi {\left(s+r_0\right)}^2{k}^2}}=\\ \frac{1}{2}\rho ·\pi k^2·v_B^2{\left(L+y+r_0\right)}^4\left\{\frac{1}{s_A+r_0}-\frac{1}{L+y+r_0}\right\}\end{array}}$

La suma de las dos energías se ha de mantener aproximadamente constante

Ejemplo

Consideremos un tubo en U de sección variable tal que

• r₀=10 cm
• k=1 mm
• L=20 cm

Las condiciones iniciales son: en el instanet t=0, se desplaza la supoerficie libre del fluido y=1 mm y y se suelta dy/dt=0

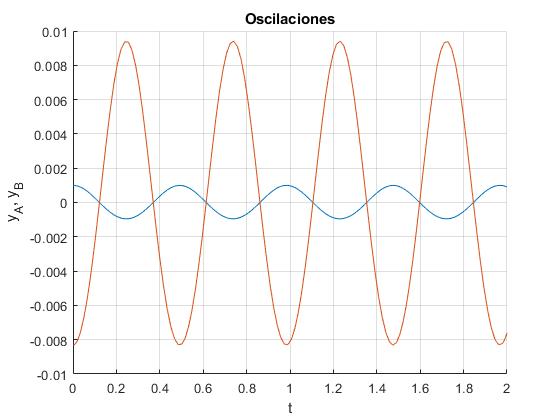
Representamos la posición de la superficie libre derecha y_B=y y la izquierda y_A=-s_A en función del tiempo t

function tubo_U
    r0=0.1;
    L=0.2; 
    k=0.001;
    [t,x]=ode45(@tubo,[0,2],[0.001,0]);
    hold on
    plot(t,x(:,1)) %movimiento B
    sA=(r0^3+(x(:,1)+L+r0).^3-(L+r0)^3).^(1/3)-r0;
    plot(t,-sA) %movimiento A, y_A=-sA
    hold off
    grid on
    xlabel('t')
    ylabel('y_A, y_B');
    title('Oscilaciones')
%energía
    Ep=9.8*((L+x(:,1)).^4/4-L^4/4+(2*r0-L)*((L+x(:,1)).^3/3-L^3/3)+r0*
(r0-2*L)*((L+x(:,1)).^2/2-L^2/2)-L*r0^2*x(:,1)+sA.^4/4+2*r0*sA.^3/3+r0^2*sA.^2/2);
    Ek=((x(:,2).^2).*(L+x(:,1)+r0).^4).*(1./(sA+r0)-1./(L+x(:,1)+r0))/2;
    disp(Ek+Ep)
    
    function z=tubo(~,x)   
        sA=(r0^3+(x(1)+L+r0)^3-(L+r0)^3)^(1/3)-r0;
        A_a=pi*(sA+r0)^2*k^2;
        A_b=pi*(L+x(1)+r0)^2*k^2;
        num=A_b*(1/(sA+r0)-1/(L+x(1)+r0))/(pi*k^2);
        z=[x(2); -(9.8*(x(1)+sA)+((1-A_b^2/A_a^2)/2+2*((L+x(1)+r0)/(sA+r0)-1))
*x(2)^2)/num]; 
    end
end

Comprobamos que la energía se mantiene aproximadamente constante

 1.0e-05 *
    0.4222
    0.4222
    .....
    0.4214
    0.4214
    0.4214    

Ecuación de Bernoulli no estacionaria

El flujo Q no es constante, por lo que aplicamos aplicamos la ecuación de Bernoulli en el estado no estacionario a los puntos A y B situados en la superficie libre del fluido a uno y otro lado del tubo en U

${\displaystyle \begin{array}{l}\left(p_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2\right)-\left(p_2+\rho g{y}_2+\frac{1}{2}\rho v_2^2\right)=\frac{dQ}{dt}{\displaystyle \underset{1}{\overset{2}{\int }}\frac{ds}{A(s)}}\\ Q=\frac{dm}{dt}=\rho Av\end{array}}$

El punto 1 es A, -s_A, y el 2 es B, s_B=L+y

${\displaystyle \begin{array}{l}\left(p_0-\rho g{s}_A+\frac{1}{2}\rho v_A^2\right)-\left(p_0+\rho gy+\frac{1}{2}\rho v_B^2\right)=\rho \frac{d\left(vA\right)}{dt}\underset{s_A}{\overset{L+y}{{\displaystyle \int }}}\frac{ds}{A(s)}\\ \frac{d\left(vA\right)}{dt}=A\frac{dv}{dt}+v\frac{dA}{dt}=A\frac{dv}{dt}+v\frac{dA}{ds}\frac{ds}{dt}=A\frac{dv}{dt}+v^2\frac{dA}{ds}\end{array}}$

Por la ecuación de continuidad

${\displaystyle \begin{array}{l}Q=\rho A(s_A)v_A=\rho A(s_B)v_B\\ v_B=\frac{d{s}_B}{dt}=\frac{dy}{dt}\\ v_A=\frac{A(L+y)}{A(s_A)}\frac{dy}{dt}\end{array}}$

El primer miembro de la ecuación es

${\displaystyle -\rho g\left(s_A+y\right)+\frac{1}{2}\rho \left({\left(\frac{A(L+y)}{A(s_A)}\right)}^2-1\right){\left(\frac{dy}{dt}\right)}^2}$

El segundo miembro

${\displaystyle \rho \frac{d\left(vA\right)}{dt}\underset{s_A}{\overset{s_B}{{\displaystyle \int }}}\frac{ds}{A(s)}=\rho \left(A(y+L)\frac{d^{2}y}{d{t}^2}+{\left(\frac{dy}{dt}\right)}^2{\frac{dA}{ds}|}_{y+L}\right){\displaystyle \underset{s_A}{\overset{L+y}{\int }}\frac{ds}{A(s)}}}$

Simplificando la densidad, ρ e igualando ambos miembros, obtenemos la misma ecuación diferencial en y que aplicando la conservación de la energía

${\displaystyle \frac{1}{2}{\left(\frac{dy}{dt}\right)}^2\left\{1-\frac{A^2(L+y)}{A^2(s_A)}\right\}+g(y+s_A)+\left\{{\left(\frac{dA(s)}{ds}\right)}_{L+y}{\left(\frac{dy}{dt}\right)}^2+A(L+y)\frac{d^{2}y}{d{t}^2}\right\}\underset{s_A}{\overset{L+y}{{\displaystyle \int }}}\frac{ds}{A(s)}=0}$

Referencias

Carl E Mungan, Garth A Sheldon-Coulson. Liquid oscillating in a U-tube of variable cross section. Eur. J. Phys. 42 (2021) 025008

Artículo disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017